高等数学·极限

极限

极限的定义

1）数列极限

\[\begin{align} &\lim_{n \rightarrow \infty}{x_n}=A \Leftrightarrow对于\forall \epsilon0,\exist N,使得当nN时,有|x_n-A|<\epsilon\\ &\lim_{x\rightarrow \infty}f(x)=A\Leftrightarrow \forall \epsilon0,\exist M0,使得当|x|M时,有|f(x)-A|<\epsilon\\ &\lim_{x\rightarrow +\infty}f(x)=A\Leftrightarrow \forall \epsilon0,\exist M0,使得当xM时,有|f(x)-A|<\epsilon\\ &\lim_{x\rightarrow -\infty}f(x)=A\Leftrightarrow \forall \epsilon0,\exist M0,使得当x<M时,有|f(x)-A|<\epsilon\\ &\lim_{x\rightarrow x_0}f(x)=A\Leftrightarrow \forall \epsilon0,\exist M0,使得当xM时,有|f(x)-A|<\epsilon\\ \end{align} \]

极限的性质

1）局部保号性

\[\begin{align} &若\lim_{x\rightarrow x_0}f(x)=A0(<0),\\ &则\exist \delta 0,使得当x \in U^0(x_0,\delta)时,f(x)0(<0)\\ \end{align} \]

推论：保序性：

\[\begin{align} &若\lim_{x\rightarrow x_0}f(x)=A0(<0),则\forall \alpha <A(\beta A),\\ &\exist \delta0,使得当x \in U^0(x_0,\delta)时,f(x)\alpha(f(x)<\beta)\\ \end{align} \]

2）局部有界性

\[\begin{align} 若\lim_{x\rightarrow x_0}f(x)=A,则\exist U^0(x_0),使得f(x)在U^0(x_0)内有界 \end{align} \]

3）不等式性质

\[\begin{align} &若\lim_{x \rightarrow x_0}f(x)=A,\\ &\lim_{x \rightarrow x_0}g(x)=B都存在,\\ &且f(x)\geq g(x),\\ &则A\geq B\\ &\\ &注解：若将f(x)\geq g(x)条件换为f(x)g(x),结论AB不一定成立\\ &x\rightarrow +\infty,\frac{1}{x}\frac{1}{x+1}不能推出\lim_{x\rightarrow +\infty}\frac{1}{x}\lim_{x\rightarrow +\infty}\frac{1}{x+1}\\ &但可以推出\lim_{x\rightarrow +\infty}\frac{1}{x}\geq\lim_{x\rightarrow +\infty}\frac{1}{x+1} \end{align} \]

推论：

\[若\lim_{x\rightarrow x_0}存在,且f(x)\geq0(\leq 0),则A\geq 0(A\leq 0) \]

4）四则运算

\[\begin{align} &若\lim f(x)=A,\lim g(x)=B,则\\ &\lim [f(x) \pm g(x)]=A \pm B\\ &\lim f(x)g(x)=A*B\\ &\lim \frac{f(x)}{g(x)}=\frac{A}{B},(B \neq 0)\\ &\\ &注解：若\lim f(x)不存在,\lim g(x)=B存在,\\ &则\lim [f(x) \pm g(x)]必不存在,\\ &但\lim f(x)g(x)不一定必存在\\ &\\ \end{align} \]

数列极限

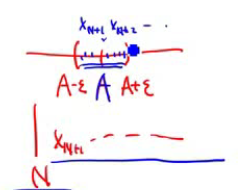
\[\begin{align} &定义1 \lim_{n\rightarrow \infty}x_n=A:\\ &\forall \epsilon0,\exist N0,当nN时,恒有|x_n-A|<\epsilon\\ &注解：\\ &(1)\epsilon与N的作用：\\ &\epsilon刻画x_n与A的接近程度,N是描述n\rightarrow \infty的过程\\ &(2)几何意义：\\ &对任意一个给定的\epsilon，在\epsilon领域，当n足够大时，前有限项落在领域外，其余都落在(A-\epsilon,A+\epsilon)内\\ \end{align} \]

\[\begin{align} &(3)一个数列有没有极限与前有限项无关\\ \end{align} \]

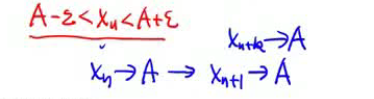
\[\begin{align} &(4)\lim_{n\rightarrow\infty}x_n=a\Leftrightarrow\lim_{k\rightarrow\infty}x_{2k-1}=\lim_{k\rightarrow\infty}x_{2k}=a:\\ &数列极限\exist\overset{\Rightarrow}{\nLeftarrow}奇数列偶数列极限\exist\\ &数列极限\exist\overset{\Rightarrow}{\Leftarrow}奇数列极限\exist=偶数列极限\exist\\ &eg:a_n=(-1)^n,a_{2k-1}=-1,-1,-1,...,-1;a_{2k}=1,1,1,...,1;\lim_{k\rightarrow \infty}a_{2k-1}\neq\lim_{k\rightarrow \infty}a_{2k} \end{align} \]

例题1

\[\begin{align} &法1：分奇偶数列\\ &奇数项：\lim_{n\rightarrow\infty}(\frac{n+1}{n})^{-1}=1\\ &偶数项：\lim_{n\rightarrow\infty}(\frac{n+1}{n})^{1}=1\\ &法2：缩放法+夹逼原理\\ &(\frac{n+1}{n})^{-1}\leq(\frac{n+1}{n})^{(-1)^n}\leq\frac{n+1}{n}\\ &\lim_{n\rightarrow \infty}(\frac{n+1}{n})^{-1}=1\leq\lim_{n\rightarrow \infty}(\frac{n+1}{n})^{(-1)^n}\leq\lim_{n\rightarrow \infty}\frac{n+1}{n}=1\\ &I=\lim_{n\rightarrow \infty}(\frac{n+1}{n})^{(-1)^n}=1\\ \end{align} \]

例题2

\[\begin{align} &(1)解法:重要不等式||a|-|b||\leq|a-b|\\ &因为\lim_{n\rightarrow\infty}x_n=a由极限定义可知\\ &\forall \epsilon0,\exist N0,当nN时,|x_n-a|<\epsilon\\ &根据||x_n|-|a||\leq|x_n-a|,\\ &则\forall \epsilon0,\exist N0,当nN时,||x_n|-|a||<\epsilon\\ &反之不成立,例如x_n=(-1)^n,则\lim_{n\rightarrow \infty}|x_n|=1=|1|,但\lim_{n\rightarrow \infty}(-1)^n不存在\\ &(2)由(1)可知,若\lim_{n\rightarrow\infty}x_n=0,则\lim_{n\rightarrow \infty}|x_n|=|0|=0\\ &由\lim_{n\rightarrow\infty}|x_n|=0,\forall \epsilon0,\exist N0,当nN时,||x_n|-0|<\epsilon\\ &即|x_n-0|<\epsilon\\ \end{align} \]

求数列极限的方法：

\[\begin{align} &（1）将数列极限转化为函数极限\\ \end{align} \]

函数极限

1)自变量趋于无穷大时函数的极限

例题

\[\begin{align} &极限\lim_{x\rightarrow \infty}\frac{\sqrt{x^2+1}}{x}=?\\ &解：\\ &\sqrt x^2=|x|\\ &分左右\\ &\lim_{x\rightarrow +\infty}\frac{x\sqrt{1+\frac{1}{x^2}}}{x}=1\\ &\lim_{x\rightarrow -\infty}\frac{x\sqrt{1+\frac{1}{x^2}}}{x}=-1\\ &\lim_{x\rightarrow -\infty}\frac{x\sqrt{1+\frac{1}{x^2}}}{x}\neq\lim_{x\rightarrow +\infty}\frac{x\sqrt{1+\frac{1}{x^2}}}{x}\\ &\lim_{x\rightarrow \infty}\frac{\sqrt{x^2+1}}{x}不存在 \end{align} \]

2)自变量趋于有限值时函数的极限

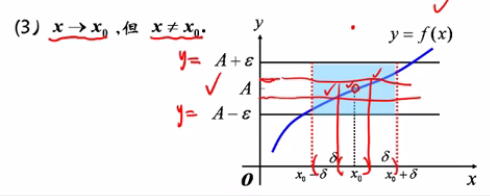
\[\begin{align} &注解：(1)\epsilon的任意性,\epsilon与\delta时,恒有|f(x)-A|<\epsilon\\ &\Rightarrow A-\epsilon<f(x)<A+\epsilon\\ &(2)几何意义：f(x_0)这一点可无定义，与去心邻域的函数值有关系\\ \end{align} \]

易错点：

\[\begin{align} &正确：\lim_{x\rightarrow 0}\frac{\sin x}{x}=1(x\rightarrow 0,x\neq 0)\\ &错误：\lim_{x\rightarrow 0}\frac{\sin(x\sin \frac{1}{x})}{x\sin\frac{1}{x}}=1\\ &需保证x{\sin\frac{1}{x}}\rightarrow 0,x{\sin\frac{1}{x}}\neq 0\\ &即在0点的去心领域内x{\sin\frac{1}{x}}\neq0\\ &但当x=\frac{1}{n\pi},使得x{\sin\frac{1}{x}}=0\\ &所以原始极限不存在\\ \end{align} \]

极限性质

\[\begin{align} &1)有界性\\ &(1)数列有界性：如果数列[x_n],那么数列[x_n]一定有界\\ &x_n\rightarrow a,nN,因为x_n\leq M \end{align} \]

\[\begin{align} &x_n前n项为有限元,必有一个数M大于前n项最大值\\ &收敛\overset{\Rightarrow}{\nLeftarrow}有界\\ &eg:x_n=(-1)^n\\ &(2)局部有界性：若\lim_{x\rightarrow x_0}f(x)\exist,则f(x)在x_0某去心邻域有界\\ &\lim_{x\rightarrow x_0}f(x)\exist\overset{\Rightarrow}{\nLeftarrow}f(x)局部有界(去心邻域有界)\\ &eg:f(x)=\sin\frac{1}{x},\lim_{x\rightarrow 0}{\sin\frac{1}{x}}有界,但不存在\\ &2)保号性\\ &(1)数列极限保号性\\ &设\lim_{n\rightarrow \infty}{x_n}=A\\ &[1]如果A0(或A<0),则存在N0,当nN,x_n0(或x_n<0)\\ &[2]如果存在N0,当nN时,x_n\geq 0(或x_n\leq0),则A\geq0(或A\leq 0)\\ &(2)函数极限保号性\\ &[1]如果A0(或A<0),则存在\delta0,当x\in \dot{U}(x_0,\delta)时,f(x)0(或f(x_0)<0)\\ &[2]如果存在\delta0,当x\in \dot{U}(x_0,\delta)时,f(x)\geq0(或f(x)\leq0),那么A\geq0(或A\leq0) \end{align} \]