高等数学·函数
函数
定义: 二要素:定义域&对应关系
例题:
基本初等函数:
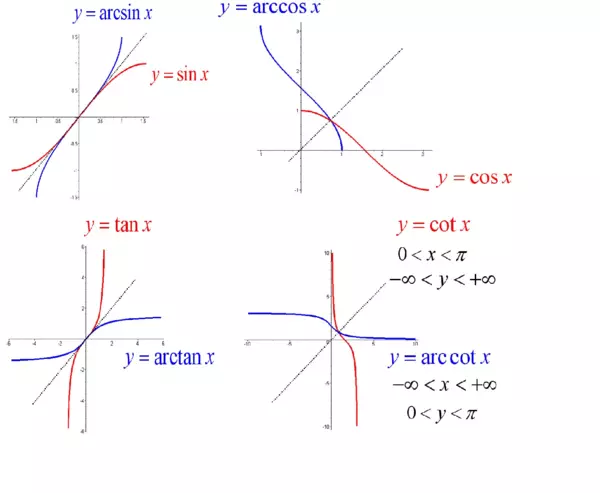
arcsinx&sinx
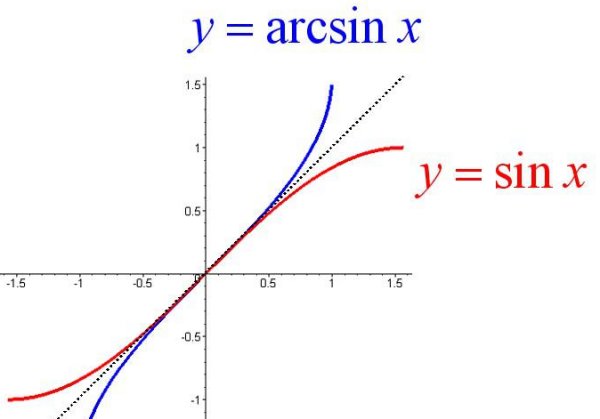
arccosx&cosx
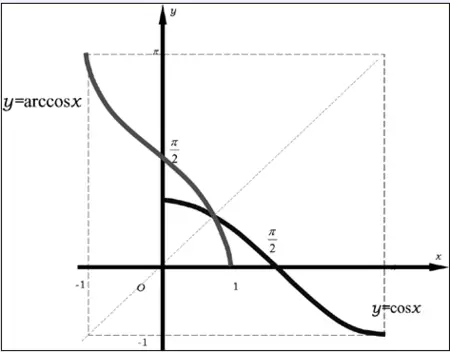
arctanx&tanx
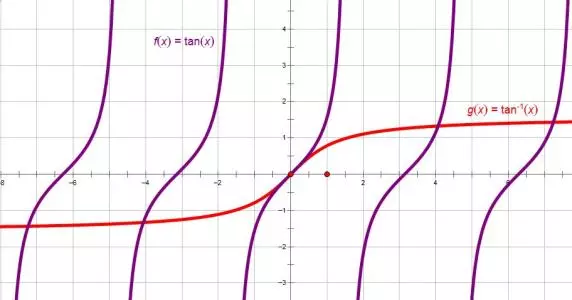
arccotx&cotx
常用的三角恒等:
函数性质
1)奇偶性
判断奇偶性的方法:
(1)定义
(2)奇偶函数的四则运算:奇函数代数和为奇函数,偶函数的代数和为偶函数,奇函数和偶函数的乘积为奇函数
(3)奇函数的复合运算:内外函数至少一个为偶函数,则复合函数为偶函数,奇函数与奇函数复合为奇函数
(4)奇函数的导数为偶函数,偶函数的导函数为奇函数,奇函数的原函数为偶函数,但偶函数的原函数未必为奇函数
2)周期性
3)单调性
初等函数
由基本初等函数经四则运算以及复合运算后得到的函数
一个初等函数的绝对值还是初等函数
函数有界性
判定有界性方法:
判定函数无界方法:
例题:
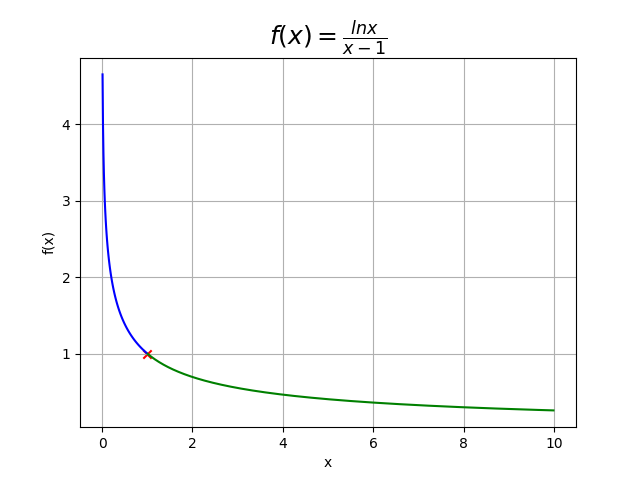
复合函数
例题:
反函数
注解:
例题:





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列1:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· Apache Tomcat RCE漏洞复现(CVE-2025-24813)