高等数学·多元函数微分学
第四章 多元函数微分学
第一节 基本概念机结论
定义1:(二元函数)
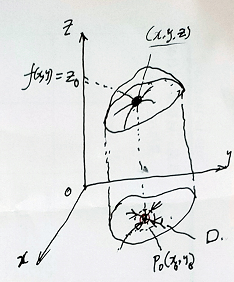
例题
定义2:(二元函数的极限)
例题
注解:
定义3(二院函数的连续性)
定理1

定义4(偏导数)
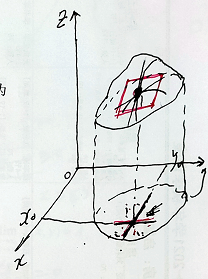
例题

定义5(全微分)
注解:
定理2
定理3 几个命题之间的关系
二元函数可微与偏导的联系 - blueflylabor - 博客园 (cnblogs.com)
例题

注解:


第二节 多元函数微分法
初等函数的微分法

注解:
例题
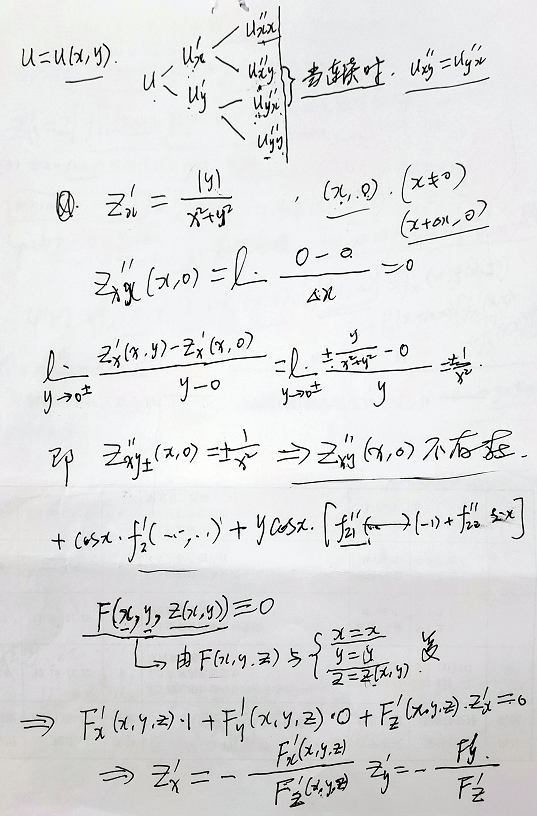
复合函数微分法


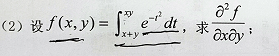
多元隐函数的微分法
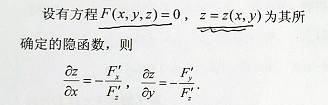
例题:
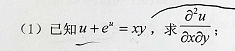

多元函数的极值与最值求法



无条件极值(二元)
有界闭区域
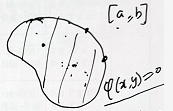
解题步骤
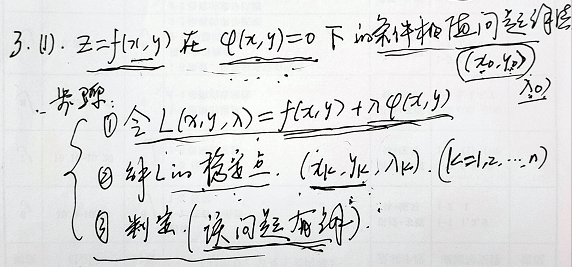

例题:







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通