高等数学·微分方程

微分方程

一、常微分方程的基本概念

1.微分方程

\[y'=2x \]

含有未知函数的导数或微分的方程

2.微分方程的阶

\[1阶方程 \]

微分方程中所出现的未知函数最高阶导数的阶数

3.微分方程的解

\[y=f(x)=x^2 \]

满足微分方程的函数

4.微分方程的通解

\[y=f(x)=x^2+c \]

如果微分方程的解中包含任意常数，且任意常数的个数与微分方程的阶数相同

5.微分方程的特解

\[y=f(x)=x^2+1 \]

微分方程的不含任意常数的解

6. 初始条件

确定特解的一组常数

7.积分曲线

方程的一个解在平面上对应一条曲线

二、一阶微分方程 y'=f(x,y)

1.可分离变量的方程

\[\begin{align} &y'=f(x)g(y)\Leftrightarrow \frac{dy}{dx}=f(x)g(y)\Leftrightarrow \frac{dy}{g(y)}=f(x)dx \\ &求解方法对两端积分\Leftrightarrow \int\frac{dy}{g(y)}=\int f(x)dx\\ \end{align} \]

2.齐次微分方程

\[\begin{align} &\frac{dy}{dx}=\Phi(\frac{y}{x})\\ &方法：令u=\frac{y}{x},y=ux,y'=u+u'x\\ \end{align} \]

例题

\[\begin{align} &y'+\frac{y}{x}=(\frac{y}{x})^2\\ &令u=\frac{y}{x},y=ux,y'=u+u'x\\ &\Leftrightarrow u+u'x+u=u^2\\ &\Leftrightarrow u+\frac{du}{dx}x+u=u^2\\ &\Leftrightarrow \frac{du}{u^2-2u}=\frac{1}{x}dx\\ &\Leftrightarrow \int\frac{du}{u^2-2u}=\int\frac{1}{x}dx\\ &\Leftrightarrow \frac{1}{2}(\ln|u-2|-\ln|u|)=\ln|x|+C\\ &\Leftrightarrow \frac{u-2}{u}=Cx^2\\ \end{align} \]

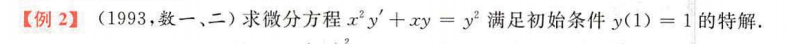
3.一阶线性微分方程

\[\begin{align} &形如y'+p(x)y=Q(x)\\ &通解：y=e^{-\int p(x)dx}[\int Q(x)e^{\int p(x)dx}+C]\\ \end{align} \]

4.伯努利方程

\[\begin{align} &形如y'+p(x)y=Q(x)y^n(n \neq 0,1)\\ &方法：令u=y^{1-n}\\ &y^{-\alpha}y'+p(x)y^{1-\alpha}=Q(x)\\ &令u=y^{1-\alpha}\\ &(1-\alpha)y^{-\alpha}y'=\frac{du}{dx}\\ \end{align} \]

\[\begin{align} &观察到微分方程中包含y''和y'和y,该方程为y''=f(y,y')型\\ &令y'=p,y''=p\frac{dp}{dy}\\ &得yp\frac{dp}{dy}+p^2=0\\ &\Leftrightarrow y\frac{dp}{dy}+p=0\\ &当p=0时,该方程成立,但跟据初始条件y|_{x=0}=1\\ &即p=1与其不符\\ &\Leftrightarrow \int\frac{dp}{p}=-\int\frac{dy}{y}\\ &\Leftrightarrow |py|=e^c\\ &\Leftrightarrow p=\frac{c}{y}\\ &\Leftrightarrow \frac{dy}{dx}=\frac{c}{y}\\ &根据初始条件y'|_{x=0}=\frac{1}{2}\Leftrightarrow c=\frac{1}{2}\\ &\Leftrightarrow y^2=x+c\\ &跟据初始条件y|_{x=0}=1,y^2=x+1\\ &又y|_{x=0}=10,y=\sqrt{x+1} \end{align} \]

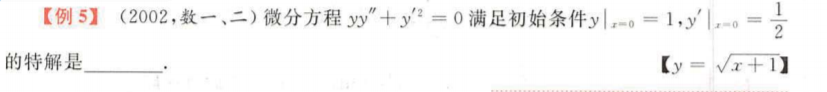
##### 5.全微分方程

三、可降阶的高阶方程

\[\begin{align} &y'=p=\frac{dy}{dx},y''=\frac{dp}{dx}\\ &y''=f(x,y')\Leftrightarrow\frac{dp}{dx}=f(x,p) \end{align} \]

\[\begin{align} &x\frac{dp}{dx}+3p=0\\ &\int{\frac{1}{p}dp}=-\frac{1}{3}\int{\frac{1}{x}dx}\\ &p=\frac{c}{x^3}\\ &\frac{dy}{dx}=\frac{c}{x^3}\\ &y=\frac{c_2}{x^2}+c_1\\ \end{align} \]

\[\begin{align} &y'=p=\frac{dy}{dx},y''=\frac{dp}{dx}\\ &可得\frac{dp}{dy}=f(y,p)无解\\ &令y'=p=\frac{dy}{dx},y''=\frac{dp}{dx}=\frac{dp}{dy}p\\ &得\frac{dp}{dx}p=f(y,y')\\ \end{align} \]

\[\begin{align} &y\frac{dp}{dy}p+p^2=0\\ &\int\frac{dp}{p}=-\int\frac{dy}{y}\\ &py=c\\ &p=\frac{c}{y}\\ &\frac{dy}{dx}=\frac{c}{y}\\ &因为y'|_{x=0}=\frac{1}{2}\\ &\frac{dy}{dx}=\frac{\frac{1}{2}}{y}\\ &y^2=x+c\\ &因为y|_{x=0}=1\\ &y=\sqrt{x+1} \end{align} \]

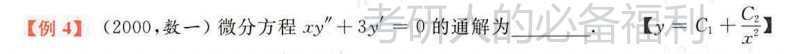
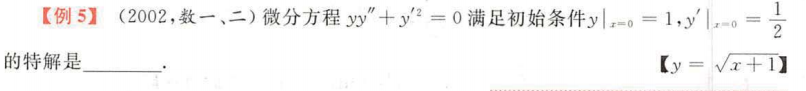
四、高阶线性微分方程

\[\begin{align} &y''+py'+qy\Leftrightarrow r^2+pr+q=0\\ &共轭复根求法：x_{1},x_2=\frac{-b\pm i\sqrt{4ac-b^2}}{2a}(i^2=-1)\\ &例：y=xe^x是y''+py'+qy=0的解，\\ &(r-1)^2=0\\ &r^2-2r+1=0\\ &p=-2,q=1\\ \end{align} \]

\[\begin{align} &r^2-r+\frac{1}{4}=0\\ &(r-\frac{1}{2})^2=0\\ &r_1=r_2=\frac{1}{2}\\ &y=e^{\frac{1}{2}x}(C_1+C_2x)\\ \end{align} \]

\[\begin{align} &r^2+2r+5=0\\ &r_{1,2}=\frac{-2\pm i\sqrt{4-20}}{2}=-1\pm 2i\\ &y=e^{-x}(C_1\cos{2x}+C_2\sin{2x}) \end{align} \]

\[\begin{align} &r^3-2r^2+r-2=0\\ &r^2(r-2)+r-2=0\\ &(r-2)(r^2+1)=0\\ &r_1=2,r_{2,3}=\pm i\\ &y=C_1e^{2x}+C_2\cos{x}+C_3\sin{x}\\ \end{align} \]

\[\begin{align} &解法核心：找到齐次特解\\ \end{align} \]

\[\begin{align} &D=\frac{d}{dt}\\ &令x=e^t或t=\ln x,t'=\frac{dt}{dx}=\frac{1}{x}\\ &y'=\frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}=\frac{1}{x}\frac{dy}{dt}\\ &xy'=\frac{dy}{dt}=Dy\\ &y''=(\frac{1}{x}\frac{dy}{dt})'=(\frac{dy}{dt})'\frac{1}{x}-\frac{1}{x^2}\frac{dy}{dt}=\frac{d^2y}{dt^2}\frac{dt}{dx}\frac{1}{x}-\frac{1}{x^2}\frac{dy}{dt}=\frac{d^2y}{dt^2}\frac{1}{x^2}-\frac{1}{x^2}\frac{dy}{dt}=D(D-1)y\\ \end{align} \]

\[\begin{align} &D(D-1)y+4D+2y=0\\ &r^2-r+4r+2=0\\ &(r+1)(r+2)=0\\ &y=C_1e^{-t}+C_2e^{-2t}\\ &y=\frac{C_1}{x}+\frac{C_2}{x^2}\\ \end{align} \]

例题

1.

\[\begin{align} &若二阶常系数线性齐次微分方程y''+ay'+by=0的通解为y=(C_1+C_2x)e^x,\\ &则非齐次方程y''+ay'+by=x满足条件y(0)=2,y'(0)=0的通解为？\\ &解：\\ &由线性齐次微分方程的通解可知r=1是齐次方程的特征方程的二重根，\\ &则齐次方程的特征方程为(r-1)^2=0,r^2-2r+1=0\\ &可得a=-2,b=1\\ &非齐次方程为y''-2y'+y=x,即x=e^{0x}x,解为线性解y*=a'x+b'\\ &带入非齐次方程得0-2a'+a'x+b'=0\\ &a'=1,b'=2\\ &则非齐次方程的通解为y=(C_1+C_2x)e^x+x+2\\ &根据y(0)=2,y'(0)=0,得到y=x(1-e^x)+2\ \end{align} \]

2.

\[\begin{align} &设y=\frac{1}{2}e^{2x}+(x-\frac{1}{3})e^x是二阶常系数非齐次线性微分方程\\ &y''+ay'+by=ce^x的一个特解,则a,b,c各为多少？\\ &解：\\ &y=\frac{1}{2}e^{2x}+xe^x-\frac{1}{3}e^x对应y=ay_1+by_2+y^*\\ &可知r=2,r=1是齐次方程的两个线性无关解\\ &特征方程为(r-1)(r-2)=0,r^2-3r+2=0\\ &a=-3,b=2,y''-3y'+2y=ce^x,将非线性解带入\\ &\begin{cases}&y'=e^x+xe^x\\&y''=2e^x+xe^x\\\end{cases}\\ &得c=-1\\ &a,b,c=-3,2,-1\\ \end{align} \]