笛卡尔树

  定义：笛卡尔树是一种特定的二叉树数据结构，可由数列构造，在范围最值查询、范围top k查询（range top k queries）等问题上有广泛应用。它具有堆的有序性，中序遍历可以输出原数列

  总的来说就是，二叉查找树+堆

  给定下列序列，那么构造出来的就是如图的东西。  

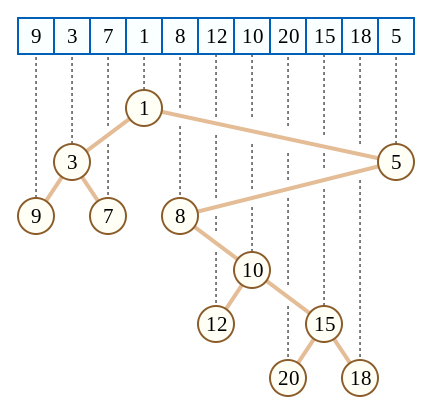
你可以发现一个有趣的性质，RMQ(L,R)=LAC(L,R)

这也应该是这个数据结构比较有意思的地方把

构造方法其实很简单

下面给出笛卡尔树的正规代码：

int creat(int n)
{
    top=1;
    stacks.push_back(1);
    for (int i=2;i<=n;i++){
        //找到栈里面第一个大于等于大的数，
        while(top>0 && T[i].val<T[stacks[top]].val){
                top--;
        }
        if (top>0)
        {
            T[i].f=stacks[top];//把这个点节点的父亲节点设置为栈顶根节点
            T[i].l=T[stacks[top]].r;//由于存放在T[stacks[top]].r的点是前面遍历的点，那么它应该放在新节点的左儿子，新节点的左儿子放右边的节点
            T[T[stacks[top]].r].f=i;//把右儿子的父亲节点换掉
            T[stacks[top]].r=i;//把加入新的节点
            if (top==stacks.size()-1)//顶部
            {
                top++;
                stacks.push_back(i);
            }else {
                stacks[++top]=i;
            }
        }else{
           //替换根节点
           T[stacks[1]].f=i;
           T[i].l=stacks[1];
           stacks[++top]=i;
        }
    }
    return stacks[1];
}

当然还有模板：

void build(int n,int a[],int ch[][2],int fa[]){
   tp=0;//栈指针
   for (int i=1;i<=n;i++)
   {
       int last=0;//栈顶元素
       while(tp){
          if (a[stk[tp]]<=a[i]){//如果当前的值大于栈顶
            //如果现在栈顶元素的右儿子是存在的
            //需要把栈顶元素的右儿子断掉加入新节点的左儿子，
            //同时把新节点加入栈顶元素的右儿子
             if (ch[stk[tp]][1])ch[i][0]=ch[stk[tp]][1],fa[ch[stk[tp]][1]]=i;
             ch[stk[tp]][1]=i;fa[i]=stk[tp];
             break;
          }
          last=stk[tp--];//先除去栈顶元素
       }
       //如果栈为空，并且last有值的话，把这个值加入左儿子
       if (!tp && last)ch[i][0]=last,fa[last]=i;
       stk[++tp]=i;
   }
}