“数”的起源

注：本文节选自《SOD框架"企业级"应用数据架构实战》一书之【2.1.1“数”的起源】，转发自此图书的在线试读网站，更多内容可点击了解。

2.1 数据漫话史—抽象、表示与存储

2.1.1“数”的起源

  《山海经》、《周易》、《黄帝内经》并称为"上古三大奇书"，书中记述的事情年代久远， 内容宏大而又神秘，其中都有“数术”方面的论述和演绎。《黄帝内经·素问·上古天真论》 说：

     “上古之人，其知道者，法于阴阳，和于术数，食饮有节，起居有常，不妄作劳，故能 形与神俱，而尽终其天年，度百岁乃去。”

     这段话是《黄帝内经》这部书有关人类养生方法的总则，是中国中医养生文化的起源， 而这段话，点睛之笔正是“法于阴阳，和于术数”。术数，术，技术、方法、技巧；数，理 数、气数、数字。

     《广雅》：“数，术也。”在笔者看来，这句话正揭示了数的起源和数的应用 与发展。

     在旧石器时代晚期，人类实现了由猿人到人的转变，通过使用工具进行劳动的过程使得 智力的发展出现了一个飞跃。在长期的生产生活中，原始人类观察到了日起日落，阴晴圆缺， 食物的有和无，多和少这些对立的事物状态。“阴阳”是中国上古先民对于天地万物变化的 二元状态的一种“抽象”，基于这种抽象认知，发展出一套记述这些状态的方法、技术，而 这正是数的概念起源。术数，术，技术、方法、技巧；数，理数、气数、数字。《广雅》：“数， 术也。”因此，由这种对立的二元状态创造了最初的数：“一”和“二”。注意，此时仅仅产 生了数的概念，但距离真正用符号来抽象表示产生“数字”概念，那已经是新石器时代的事 情了。

     原始人类创造了数的概念后遇到的第一个挑战就是如何表示这两个数，但此时远没有到 用“阴阳”这两个文字来表示两种状态的程度，那个时候文字还没有产生。如果你穿越到旧 石器时代晚期，你怎么向你原始族人表示“一”和“二”的概念呢？注意你没有纸和笔，原 始人也听不懂你说话，你的任务就是教会他们识别这两个数。此时，你应该用什么最合适的 方式来表示这两个数呢？用两颗石子？用两个人？对不起对面的两个原始人完全听不懂你 在说什么。用两头猎物？对不起你的本领已经完全退化哪里有能力现场给族人打两只猎物 来？… 正当你仰天长叹根本无法完成这个艰巨的任务的时候，抬头看见密密的树林突然给 了你灵感：有了，用两根树枝，两根一样长的树枝摆在地上，这个时候你准备变一个“戏法”， 将一和二的概念变化出来，因为你确信，不管是原始人还是现代人，人们对于变“戏法”总 是感兴趣的。

     第一步，在地上放一根树枝，原始人不明白你这是要干什么，所以你得“煞有其事”的 用某种神秘的舞蹈动作和声响，吸引他们的注意力，让他们过来观看。
     第二步，在地上接着再放一根树枝，原始人可能不解，你多出来一根树枝要做什么？
     第三步，你拉来两个原始人，让他们分别站在两根树枝旁边，每一根树枝指向一个人。 原始人仍然不明白你要做什么，但你们的肢体语言可能已经让他们明白你要和他们做一个游 戏。你得用某种声响来加强这种认识，比如学他们的原始语言。
     第四步，你将地上其中一根树枝从中掰断，示意树枝指向的那个原始人离开游戏“圈子”。
     第五步，你将地上另外一根树枝从中掰断，示意树枝指向的另外一个原始人也离开游戏 “圈子”。
     第六步，你向众人展示这两根掰断的树枝；紧接着，你重新拿出两根完好的树枝，邀请 人群中其他的原始人也来玩你的游戏，重复第一步到第五步的过程，让你的原始族人明白完 好的一根树枝可以代表一个人，而一根掰断的树枝表示离开一个人，两根树枝可以代表两个 人。注意，开始不要同时邀请三个人一起玩，因为这个时候原始族人还没法理解“三”这个 概念。

     友情提示：当您和您的原始族人玩这个游戏的时候，一定要有所奖赏，或者在他们吃饱 喝足了来玩这个游戏，否则，原始人也没有这么无聊陪你玩，小心打死你啊我可不负责任的， 哈哈！

     以上故事纯属虚构，是否有类似情景也因为年代太过久远而无法考证。但是，类似的这 种对“数”的概念的进行表述的行为越来越普遍了，人们逐渐发现有更多的数需要记录，从 一、二逐渐发展到三，发展到十，计数的方法有用手指头，用绳子打结，或者用石头在岩壁 上刻画线条等等。不过相比起来，“结绳计数”（如图 2-1）这种方式更科学；用手指计数， 手指易变，用来做计算过程的临时存储可以，但不适合长久保存；用刻画石头计数，结果不 方便携带。所以“结绳计数”方法就广泛流传开来了，早在《易经》中，就有“结绳而治” 的记载。到了近代，一些没有文字的民族，仍然用“结绳记事”来传播信息。

图 2-1 结绳记数

     “结绳计数”是人们对于“数”的概念理解和数的表示运用上一个重要的里程碑，它早 于文字的产生而发展的，每增加一个“节”表示增大一个数，就跟前面虚构的那个用树枝表 示数的概念一样，一根树枝表示一个人，两根树枝表示两个人，之后原始人就能明白，三根 树枝能表示三个人。在这里将使用一个重要的概念：序列。一排树枝，一串绳结，甚至一行 石子，都是用相同的事物按顺序排列组成一个“序列”，然后用序列的元素来表示一个“数”。

     “序列”的重要特点就是它的元素有大小，元素排列是有序的，总是从大到小或者从小 到大的一种顺序排列。比如现在进行数据库查询的时候，对某一列数据进行排序，排序之后 的这列数据就是一个序列。在数学概念上，序列的这个特征可以用一个“递归”函数来表示， 即序列里面的一个元素总是比它前面一个元素大某个数或者小某个数。对于一个“自然数” 序列，这个定义可以表示成“自然数序列里面，序列里面的某个元素总是比它前面一个元素 要大一个数”。 前面已经知道，古人通过事物的二元对立状态，发现了最早的自然数：“一” 和“二”。现在“我们”即将教会原始人学习一个新的数：“三”。假设您还是前面那个穿越 的现代人，你只需要再拿一根树枝，按照从上到下的顺序摆放，您告诉原始人，这可以表示 “三个原始人”。俗话说“事不过三”，以原始人当前的智力只能明白到这个数了，再教下去 也是徒劳。

     不过，虽然教会原始人学习更大的“数”很困难，但是借助于“序列”在数学上的递归 定义，可以教会计算机来表示更大的数。假设有一个自然数序列 SN，第 n 个数就是自然数 N，它总是比它之前一个自然数 m 大 1，那么这个自然数序列可以表示成：
     SN=[1 ，2，… ,m,n]
     设函数 SN(n)的作用是计算序列 SN 中的第 n 个自然数 N，得到以下函数表达式：
     N=SN(n)
     等价于下面的表达式：
     N=SN(m)+1
     这就是表示自然数 N 的递归函数定义！

     为了便于计算机处理，需要将序列进行简化，首先简化到只有两个数，也就是前面故事 里面讲的原始人最开始的认知水平，那么上面的表达式可以推导出：
     IF SN=[1,2]
     THEN M=1,N=2
     进一步简化，假设这个序列只有 1 个元素：
     IF SN=[1]
     THEN M=0,N=1
     注意：数字 0 是很久以后才出现的概念，原始人还无法理解这个数字概念，这一步骤是 为了用计算机程序计算方便才进行的推导步骤。
     进行最后的化简，假设这个序列没有任何元素，那么第 N 个元素就是 0：
     IF SN=[]
     THEN M=NULL,N=0

     上面这段对于自然数序列 SN 的函数推导过程，可以使用函数式编程语言的鼻祖--Lisp 语言来表示处理。Lisp 即列表处理语言，全名是 List Processor。Lisp 只使用了很少语法 元素就定义了一套强大的语言，它的主要数据结构就是列表，只使用很少的操作符来处理列 表，而这些操作符本身就是一个函数。所以，这里的自然数序列 SN 可以使用 Lisp 语言的列 表来表示，比如下面的表达式：

(List 1 2 3)

表示序列 SN=[1,2,3]。
     这个列表也可以表示成下面这样：
     ‘(1 2 3)
     注意，这里是用序列来表示自然数，因为对于原始人来说，当前根本没有阿拉伯数字 1， 2，3，也还没有中文数字一，二，三。那么要表示数字“三”，只能这样：
     ‘(1 1 1)
     或者
     ‘(A A A)
     或者

  ‘( )

比如手指，绳结，甚至到了现代，用随意的一个字母符号的序列也能表示“数”，比如 用 A 表示 1，用 AA 表示 2，用 AAA 表示 3… 这种表示数的方法是最简单最有效的方法，这 些符号载体是“数”最原始的载体，如果把一条打满了节的绳子看做一个“内存条”，是不 是很简单直接的理解了计算机内存的使用原理了？所以，用“序列”来表示数，真是一个伟 大的发明！

     下面，笔者使用 Lisp 语言程序来表达如何通过一个序列来定义任何一个自然数：

;LISP语言示例1 
(defun my-number (lst)
 (if (null lst)
 0
 (1+ (my-number (rest lst)))))

这段 Lisp 程序的意思是定义一个处理序列 lst 的函数 my-number,

如果序列为空
 那么 返回结果 0
 否则 1+(之前一个数)

注意，在前面设计的教原始人理解“数”的游戏中，要告诉他们怎么得到“之前一个数” 的办法很简单，直接从地上的那一排树枝的头或者尾拿掉一根树枝就好了。Lisp 的函数 rest 的功能就是去除列表的第一个元素返回剩余元素构成的表，这样，这个新的列表所表示的数 就是“之前一个数”了：

(my-number (rest lst))

下面运行 my-number 这个函数来计算任意序列所表示的数字：

 (my-number '(1 1))
     输出：2
     (my-number '(1 1 1))
     输出：3
     (my-number '(A A ))
     输出：2
     (my-number '(A A A))
     输出：3

  程序的运行效果如下图 2-2 所示:

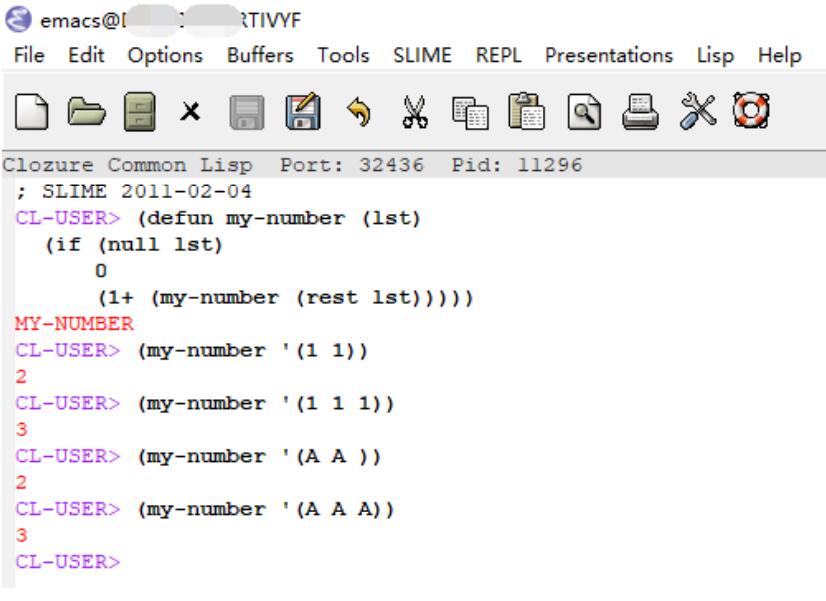
图 2-2 Lisp程序--数的序列定义示例

注：以上程序使用 Common Lisp 编写，在 LispBox 中调试通过。

     读到这里，聪明的您可能发现，这不就是求一个列表的长度么？没错，列表的长度就是 这个序列所表示的自然数的大小。这个长度可以很长，理论上，这样的列表无限长，可以表 示无限大的数。

    假设这个列表中的每一个元素所在的位置表示它所对应的数，那么这个列表就是存储这 些“数”的容器，假设它所在的位置可以通过一个指针迅速定位，通过移动指针的位置来标 记写入或者读取一个数。指针向前移动到一个位置，在这个位置写下一个标记，表示当前位 置的元素有效；在这个位置擦除之前的标记，当前位置无效，指针回退上一个元素的位置。 这个过程如图 2-3 所示。如果将这个列表看作是对一个无限长的纸带所打的孔，那么纸带就 相当于是“数”的存储器，操作纸带的机器就是一个最简单的“计算机”，上面定义处理“序 列”的函数 my-number 就是这样的计算机。实际上这个机器它就是一部“图灵机”。

图2-3 图灵机原理示意图

 

     可能思路跳跃的有点快，这里简单总结下，由事物二元对立的状态古人发现了最早的自 然数“一”和“二”，然后发展到了通过一种事物的“序列”来表示更多的自然数，古人发 明了“结绳计数”的方法。通过对“序列”的“递归定义”分析，发现了表示一个自然数内 在的数学原理，由这个原理的“程序化”定义，发现能够处理“序列”的机器就是一部“图 灵机”。有了图灵机，就能进一步处理复杂的计算问题，最终根据图灵机的原理建造了电子 计算机，直到现在的超级计算机它都没有脱离这个计算的本质。

     可见，“数”的本质就是计算。数的表示、处理就是计算的方法。《广雅》：“数，术也。” 中国先贤们的智慧实在是无比深厚啊！

     如果说“数”就是计算，那么数的存储表示就是“数据”，对“数”的处理就是计算的 方法，这个处理过程的表示就是常说的“程序”。可见“数据”和“程序”是等价的：数据 是程序，程序是数据。一种程序语言能够体现出这个特点，Lisp 真是神奇的语言！