P22 中值定理

1

2

3

4

5
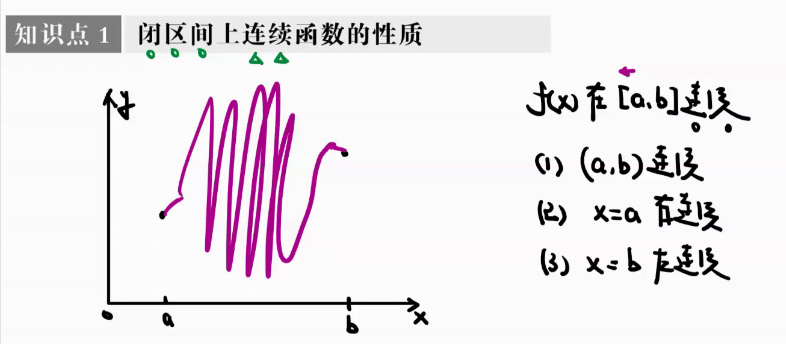
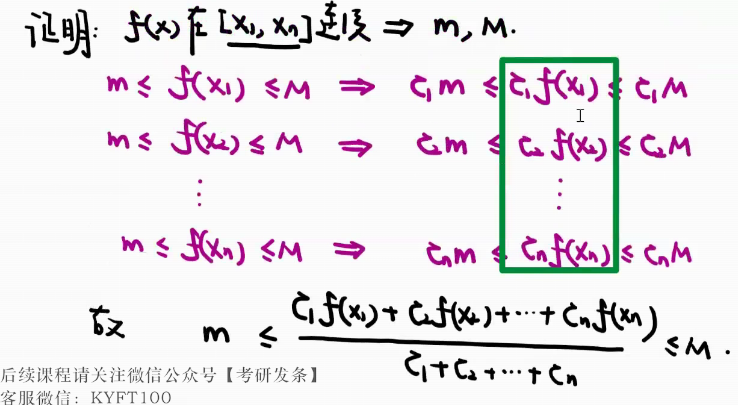
下面这题的本质就是证明一个函数等于一个数。那么怎么证明一个函数等于一个数？
就是找到最大值以及最小值，就是让下面那个圈住的被最大值和最小值夹住。那就得先用最值定理。

6
在闭区间连续，必然存在最大值和最小值。

7
平均值定理：
只要求的是平均数，那么在最大值和最小值的中间肯定会存在ξ,使得F(ξ)=平均值。

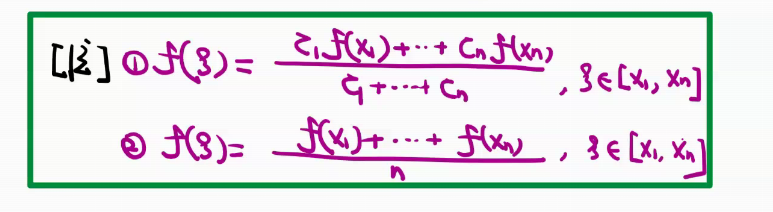
8
主意是开区间。

10
平均数就是用介值定理来证明的。

直接使用开区间就行。

介值定理：ξ∈[a,b] 在闭区间内任何一点 都可以 f（ξ）=A ，m<=A<=M; 所以用闭区间。
零点定理：ξ∈(a,b) ，f（a）*f（b）<0, 至少存在ξ∈(a,b)使得f（ξ）=0；端点的值不可能等于0，所以用开区间。
积分中值定理：ξ 的范围可以用闭区间也可以用开区间，但是习惯默认用开区间，那就用开区间吧。

11

12
闭区间连续，开区间可导（可导必连续）。为什么只提开区间呢？
因为，端点的外侧不知道什么情况，如果外侧不可导（一侧不可导，则这个点不可导），所以只提开区间就行。

对于条件三，端点值相等，又因为是连续的，开区间的作用（因为连续不一定可导），所以两点之间必然会有一个拐弯的点，这个拐弯处便是导数为0的点。

13

14
考研怎么考？
就是考某个函数使用完了罗尔定理之后的结果。
我们就是要去找到那个函数。

C要放在一边，另外的放一边。

15

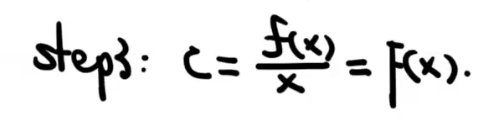
16
中值：
就是中间某一个值，并不是刚好就在中间二分之一处。

零点定理：直接设函数 F（X）=0；
罗尔定理：采用三步法；

只有一个ξ（一个中值），叫单中值问题。如果还有一个η，那就是双中值问题。

17
这就是一个ξ，带入函数中，让后全部放左边，等于0的形式，那就用零点定理。

18
这就是一个ξ，带入函数中，让后全部放左边，这是原函数F（x）求导之后等于0的结果，那就用罗尔定理。

19
这就是带入一个ξ，导函数等于0的情况，那就用罗尔定理。——————三步法。

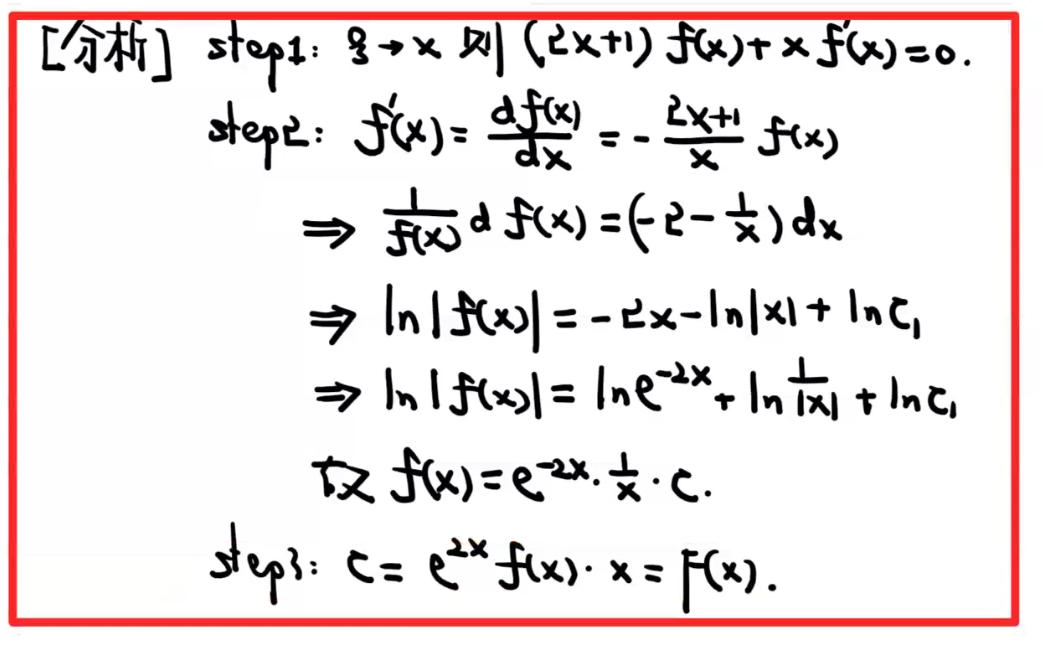
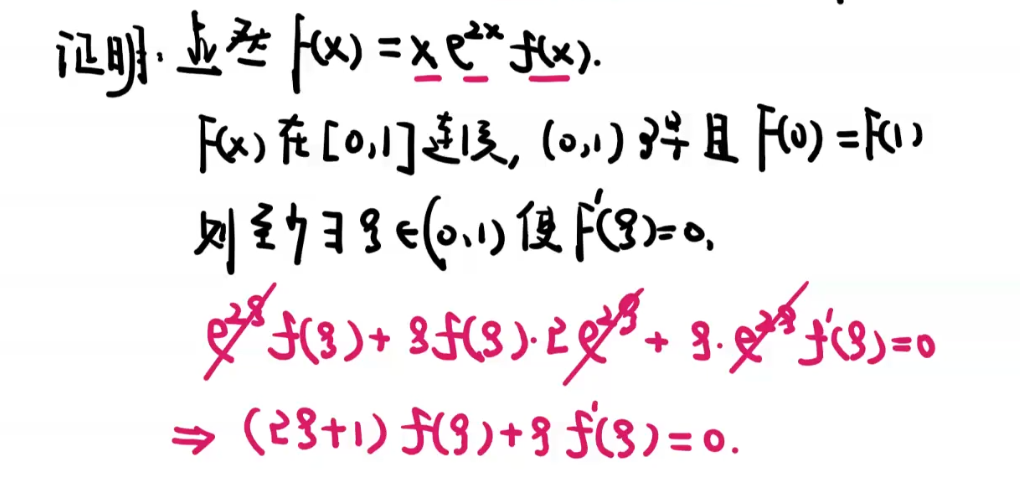
20
这一题居然要用积分中值定理来解决条件三：端点值相等。

那一步是将左右两边除以一个 e 才行成的 F（c）=F（1）；

21
在闭区间连续：

必有界，就有最大值和最小值。所以就产生了有界定理和最值定理。

然后可以知道，在最值的区间内存在某个值及其对应的x的值，便产生了介值定理，
介值介值，就是介于最大和最小值之间的值。
以上就出现了在闭区间连续条件下的三个定理。

介值定理往往会和最值定理一起用，就产生了“要想用介值，比先用最值”的说法。

还有第四个跟闭区间连续的定理：零点定理：
可以参考介值定理来记忆。介值定理：n<A<m;然后就会存在ε∈[a,b] 使得f(ε)=A;就是[a,b]中
存在一个点的值等于A；

零点定理：一个连续的曲线，两端点的值相乘小于0，则可以说明中间有一个点的值等于0；

缩略词记忆法：
“有锥再借个蛋，就能生孩子”
有：有界定理；锥：就是最，最值定理；借：就是介值定理；蛋：就是零，零点定理；

----------------------------------------------------------------------------------

积分中值定理：

条件也是闭区间连续，对一个函数进行积分的结果可以写成：
在闭区间中的某个值的函数乘以区间的长度。
就是将不规则矩形的面积换成规则矩形的面积来计算，
关键就是要找出规则矩形的高度f（ε），a<ε<b，对后面的范围用开区间就行。 

接下来学习微分中值定理：

1，费马引理：
        若f（x）在X0处取极值，且f'(X0)存在，则f'(X0)=0；
    ---费马引理讲废话，一个函数在一个点处取极值，且这个点的导数存在，肯定为0；    

2，罗尔定理
       闭区间连续，开区间可导，端点值相等，则中间存在一点的导数值为0；   
    ---我怎么理解？想一条连续的曲线，闭区间连续，开区间可导就是说除了端点不可导，
       内部都可导，只要端点值相等，那么中间就一定会有拐弯的地方，导数为0；
       罗尔（箩儿）听起来就像一个箩筐，两边是等高的，中间一定会有趋于平坦地方，
       那便是导数为0的地方。

费马引理想成凸曲线；罗尔定理想成一个凹曲线；再想到它们的定义就记起来了。   
费马引理讲废话，罗尔定理像箩儿。

这一节的考点习题：

主要就是考罗尔定理和零点定理的应用；
闭区间连续，开区间可导，给一个 ε 求等式成立的问题；形式是 F’（x）=0 就用罗尔定理；
闭区间连续给一个 ε 求等式成立的问题；形式是 F（x）=0 就用零点定理；
闭区间连续给一个 ε 求函数f（x）= A 一个数的问题，考介值定理；

四个闭区间连续就行：
1，有界定理；
2，最值定理；
3，介值定理；
4，零点定理；

一个积分中值定理
    条件：闭区间连续，然后将定积分转化为导数乘上区间长度   ε∈（a，b）。

五个微分中值定理：
1，费马引理；
2，罗尔定理；
3，拉格朗日中值定理；
4，柯西中值定理（暂时不学）；
5，泰勒公式有两个余项：皮亚诺余项；拉格朗日余项；