环境光照和球谐函数

球谐函数

Spherical Harmonics

输入：x,y,z 三维，表示一个空间方向，或者球面坐标系下表示方位角的两个角度。

输出：v 一维

组成：函数本身有一系列基函数以及其对应系数组成

定义：

\[f(\omega) = \sum_{i}{c_i B_i(\omega)} \]

可视化：

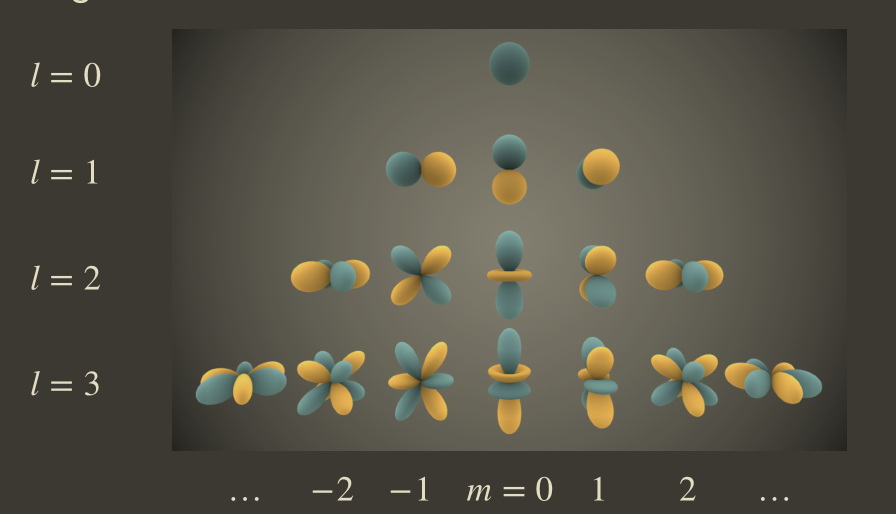
基函数分为若干阶（参数L），第L阶基函数总共含有2L+1个基函数，L阶球谐函数总共由1+3+....+(2L+1) = (L+1)^2 个基函数组成。

越高阶基函数中含有更多高频信息。

code:

double EvalSH(int l, int m, const Eigen::Vector3d& dir) {
  if (l <= kHardCodedOrderLimit) {
    // Validate l and m here (don't do it generally since EvalSHSlow also
    // checks it if we delegate to that function).
    CHECK(l >= 0, "l must be at least 0.");
    CHECK(-l <= m && m <= l, "m must be between -l and l.");
    CHECK(NearByMargin(dir.squaredNorm(), 1.0), "dir is not unit.");

    switch (l) {
      case 0:
        return HardcodedSH00(dir);
      case 1:
        switch (m) {
          case -1:
            return HardcodedSH1n1(dir);
          case 0:
            return HardcodedSH10(dir);
          case 1:
            return HardcodedSH1p1(dir);
        }
      case 2:
        switch (m) {
          case -2:
            return HardcodedSH2n2(dir);
          case -1:
            return HardcodedSH2n1(dir);
          case 0:
            return HardcodedSH20(dir);
          case 1:
            return HardcodedSH2p1(dir);
          case 2:
            return HardcodedSH2p2(dir);
        }
      case 3:
        switch (m) {
          case -3:
            return HardcodedSH3n3(dir);
          case -2:
            return HardcodedSH3n2(dir);
          case -1:
            return HardcodedSH3n1(dir);
          case 0:
            return HardcodedSH30(dir);
          case 1:
            return HardcodedSH3p1(dir);
          case 2:
            return HardcodedSH3p2(dir);
          case 3:
            return HardcodedSH3p3(dir);
        }
      case 4:
        switch (m) {
          case -4:
            return HardcodedSH4n4(dir);
          case -3:
            return HardcodedSH4n3(dir);
          case -2:
            return HardcodedSH4n2(dir);
          case -1:
            return HardcodedSH4n1(dir);
          case 0:
            return HardcodedSH40(dir);
          case 1:
            return HardcodedSH4p1(dir);
          case 2:
            return HardcodedSH4p2(dir);
          case 3:
            return HardcodedSH4p3(dir);
          case 4:
            return HardcodedSH4p4(dir);
        }
    }

    // This is unreachable given the CHECK's above but the compiler can't tell.
    return 0.0;
  } else {
    // Not hard-coded so use the recurrence relation (which will convert this
    // to spherical coordinates).
    return EvalSHSlow(l, m, dir);
  }
}

// Hardcoded spherical harmonic functions for low orders (l is first number
// and m is second number (sign encoded as preceeding 'p' or 'n')).
//
// As polynomials they are evaluated more efficiently in cartesian coordinates,
// assuming that @d is unit. This is not verified for efficiency.
double HardcodedSH00(const Eigen::Vector3d& d) {
  // 0.5 * sqrt(1/pi)
  return 0.282095;
}

double HardcodedSH1n1(const Eigen::Vector3d& d) {
  // -sqrt(3/(4pi)) * y
  return -0.488603 * d.y();
}

double HardcodedSH10(const Eigen::Vector3d& d) {
  // sqrt(3/(4pi)) * z
  return 0.488603 * d.z();
}

double HardcodedSH1p1(const Eigen::Vector3d& d) {
  // -sqrt(3/(4pi)) * x
  return -0.488603 * d.x();
}

double HardcodedSH2n2(const Eigen::Vector3d& d) {
  // 0.5 * sqrt(15/pi) * x * y
  return 1.092548 * d.x() * d.y();
}

double HardcodedSH2n1(const Eigen::Vector3d& d) {
  // -0.5 * sqrt(15/pi) * y * z
  return -1.092548 * d.y() * d.z();
}

double HardcodedSH20(const Eigen::Vector3d& d) {
  // 0.25 * sqrt(5/pi) * (-x^2-y^2+2z^2)
  return 0.315392 * (-d.x() * d.x() - d.y() * d.y() + 2.0 * d.z() * d.z());
}

double HardcodedSH2p1(const Eigen::Vector3d& d) {
  // -0.5 * sqrt(15/pi) * x * z
  return -1.092548 * d.x() * d.z();
}

double HardcodedSH2p2(const Eigen::Vector3d& d) {
  // 0.25 * sqrt(15/pi) * (x^2 - y^2)
  return 0.546274 * (d.x() * d.x() - d.y() * d.y());
}

double HardcodedSH3n3(const Eigen::Vector3d& d) {
  // -0.25 * sqrt(35/(2pi)) * y * (3x^2 - y^2)
  return -0.590044 * d.y() * (3.0 * d.x() * d.x() - d.y() * d.y());
}

double HardcodedSH3n2(const Eigen::Vector3d& d) {
  // 0.5 * sqrt(105/pi) * x * y * z
  return 2.890611 * d.x() * d.y() * d.z();
}

double HardcodedSH3n1(const Eigen::Vector3d& d) {
  // -0.25 * sqrt(21/(2pi)) * y * (4z^2-x^2-y^2)
  return -0.457046 * d.y() * (4.0 * d.z() * d.z() - d.x() * d.x()
                             - d.y() * d.y());
}

double HardcodedSH30(const Eigen::Vector3d& d) {
  // 0.25 * sqrt(7/pi) * z * (2z^2 - 3x^2 - 3y^2)
  return 0.373176 * d.z() * (2.0 * d.z() * d.z() - 3.0 * d.x() * d.x()
                             - 3.0 * d.y() * d.y());
}

double HardcodedSH3p1(const Eigen::Vector3d& d) {
  // -0.25 * sqrt(21/(2pi)) * x * (4z^2-x^2-y^2)
  return -0.457046 * d.x() * (4.0 * d.z() * d.z() - d.x() * d.x()
                             - d.y() * d.y());
}

double HardcodedSH3p2(const Eigen::Vector3d& d) {
  // 0.25 * sqrt(105/pi) * z * (x^2 - y^2)
  return 1.445306 * d.z() * (d.x() * d.x() - d.y() * d.y());
}

double HardcodedSH3p3(const Eigen::Vector3d& d) {
  // -0.25 * sqrt(35/(2pi)) * x * (x^2-3y^2)
  return -0.590044 * d.x() * (d.x() * d.x() - 3.0 * d.y() * d.y());
}

投影（参数获取）：

Projection: obtaining the coefficients of each SH basis function

\[c_i = \int_{\Omega}{f(\omega)B_i(\omega)d\omega} \]

f(w)为原始输入，被拟合函数。

重构：获得系数后，用球谐函数简化表达原始内容

\[f(\omega) = \sum_{i}{c_i B_i(\omega)} \]

性质：