FHQ-Treap & Splay
无旋 Treap(FHQ Treap)
引入
FHQ-Treap 的功能非常强,它的操作方式使得它天生支持维护序列、可持久化等特性。并且, 它几乎涵盖了有旋 Treap 的全部功能。
由于之前浅学过的 Splay 和 Treap 都已经忘掉了,故这篇文章只记录一下 FHQ-Treap 的相关的基础内容。另,感谢范浩强发明了无旋 Treap,救我于水火之中。
参考资料:
基本思想
FHQ 的核心思想在于分裂和合并,通过给定的要求,讲原有的树分裂成两个树乃至多个,然后操作完后再把它们合并起来。
我们需要存储的信息:左孩子 \(l\),右孩子 \(r\),权值 \(val\),子树大小 \(size\) 以及 Treap 这种平衡树所特有的用来维护小根堆的 \(rnd\)。一般情况下,FHQ Treap 将权值相同的节点看成多个节点,而非 Splay 和 Treap 里把权值相同的点变成一个,所以我们不需要记录节点所存储的数的个数 \(cnt\)。
功能
更新答案
其实就是一个 pushup 操作,因为我们可能要查询前驱后继这样的信息,所以子树大小必不可少。实现也很简单。
#define lc tree[p].l
#define rc tree[p].r
il void push_up(int p)
{
tree[p].size = tree[lc].size + tree[rc].size + 1;
}
新建节点
这个也没啥好说的,就是建立一个权值为 \(val\) 的新节点,跟动态开点差不多。
il int update(int val)
{
tree[++idx] = {0,0,val,rand(),1};
return idx;
}
分裂
你会发现 FHQ-Treap 的分裂和合并有点像线段树分裂和线段树合并,所以学习线段树分裂和线段树合并可能有助于你的理解。
这里也有两种分裂方式,一种是按权值 \(val\) 分裂,另一种是按大小 \(size\) 分裂。
按权值分裂
我们给定一个值 \(v\),根据这个值 \(v\) 把一棵树分裂成两棵树,一棵树的值 \(val\leq v\),另一棵树的值 \(val > v\)。
如果当前节点 \(p\) 的 \(val\leq v\),说明 \(p\) 以及其左子树都属于分裂后的左 Treap。但是,\(p\) 的右子树也可能有一部分 \(val\leq v\),因此我们需要递归分裂右子树,把 \(\leq v\) 的那部分作为 \(p\) 的右子树。同时给定一个 \(x\),指向左 Treap 的根,这个 \(x\) 有很大作用,它是传址调用的,通过它就能在递归的过程中分裂出两个树。
如果当前节点 \(p\) 的 \(val > v\),说明 \(p\) 以及其右子树都属于分裂后的右 Treap。但是,\(p\) 的左子树也可能有一部分 \(val> v\),因此我们需要递归分裂左子树,把 \(> v\) 的那部分作为 \(p\) 的左子树。同时给定一个 \(y\),指向右 Treap 的根,同理,它也是传址调用的。
递归的边界:\(p=0\),说明无这个节点。
il void Split(int p,int v,int &x,int &y)
{
if(!p) { x = y = 0; return ; }
if(tree[p].val <= v)
{
x = p;
Split(rc,v,rc,y);
push_up(x);
}
else
{
y = p;
Split(lc,v,x,lc);
push_up(y);
}
}
具体过程可以看董晓算法来加深理解。
按大小分裂
其实没啥区别,就是把值变成 \(siz\)。
il void Split(int p,int v,int &x,int &y)
{
if(!p) { x = y = 0; return ; }
if(tree[ls].size < v)
{
x = p;
Split(rc,v-tree[p].size-1,rc,y);
push_up(x);
}
else
{
y = p;
Split(lc,v,x,lc);
push_up(y);
}
}
合并
也很像线段树合并。
我们其实就是类似于线段树合并的合并两个参数:左 Treap 的根指针 \(x\)、右 Treap 的根指针 \(y\)。这是经过分裂后的两个子树,所以我们可以保证, \(x\) 中所有节点的 \(val\) 值小于等于 \(y\) 所有节点的 \(val\) 值。
因为两个 Treap 已经有序,所以在合并的时候只需要考虑把哪个树放在上面,哪个树放在下面,也就是判断哪个树作为子树。这个,我们是利用的 \(rnd\) 值来维护小根堆实现的。
il int Merge(int x,int y)
{
if(!x || !y) return x | y;//类似线段树合并
if(tree[x].rnd < tree[y].rnd)
{
tree[x].r = Merge(tree[x].r,y);
push_up(x); //要保证treap的二叉搜索树性质
return x;//返回根节点
}
else
{
tree[y].l = Merge(x,tree[y].l);
push_up(y);
return y;
}
}
以下的功能都是利用分裂和合并实现的功能。
插入节点
我们要插入一个权值为 \(v\) 的新节点,只需要用 \(v-1\) 把平衡树按权值分裂开,然后再新建一个权值为 \(v\) 的新节点,把它和左 Treap 合并,再把这棵合并后的树和右 Treap 合并。
il void Insert(int v)
{
int x,y,z;
Split(root,v,x,y);
z = update(v);
root = Merge(Merge(x,z),y);
}
删除节点
我们要删除一个权值为 \(v\) 的新节点,需要先用 \(v\) 把平衡树按权值分裂为 \(T_x,T_z\)(左右 Treap),然后再用 \(v-1\) 把 \(T_x\) 分裂成 \(T_x,T_y\),这时候,我们把 \(T_y\) 的左右节点合并而忽略根节点,这样就能起到删除的左右,然后把这个树和 \(T_x\) 合并、再和 \(T_z\) 合并。
il void Delete(int v)
{
int x,y,z;
Split(root,v,x,z);
Split(x,v-1,x,y);
y = Merge(tree[y].l,tree[y].r);
root = Merge(Merge(x,y),z);
}
查询 \(v\) 的排名
用 \(v-1\) 分裂平衡树为 \(T_x,T_y\),那么答案就是 \(tree[x].size + 1\)。
tips:分裂后别忘了再合起来。
il int Get_Rank(int v)
{
int x,y;
Split(root,v-1,x,y);
int ans = tree[x].size + 1;
root = Merge(x,y);
return ans;
}
查询排名为 \(k\) 的值
递归找,如果 \(k \leq\) 左子树的个数,递归找左子树;如果 \(k=\) 左子树个数 \(+1\),那么就是现在这个节点;否则,找右子树,注意把左子树和根节点的排名减去。
il int Get_Val(int p,int kth)
{
if(kth <= tree[lc].size) return Get_Val(lc,kth);
else if(kth == tree[lc].size + 1) return tree[p].val;
else return Get_Val(rc,kth-tree[lc].size-1);
}
查询 \(v\) 的前驱
查询 \(v\) 的前驱,只需要以 \(v-1\) 把平衡树分裂成 \(T_x,T_y\),然后在 \(T_x\) 里找第最大值即可。
il int Get_Pre(int v)
{
int x,y;
Split(root,v-1,x,y);
int ans = Get_Val(x,tree[x].size);
root = Merge(x,y);
return ans;
}
查询 \(v\) 的后继
查询 \(v\) 的后继,只需要以 \(v\) 把平衡树分裂成 \(T_x,T_y\),然后在 \(T_y\) 里找最小值即可。
il int Get_Next(int v)
{
int x,y;
Split(root,v,x,y);
int ans = Get_Val(y,1);
root = Merge(x,y);
return ans;
}
区间翻转
见下面第二个例题。
例题
板子题。code
参考题解:
FHQ-Treap 维护区间的模板题,这个题让我们进行区间翻转。
普通平衡树实现的各种操作都是基于大小关系,它之所以能实现那么多操作,最本质的原因是它巧妙地依据元素的大小关系建树,小的元素放在左子树,大的元素放在右子树,这样中序遍历的结果就恰恰是一个递增序列。这题要实现的是对给定序列的若干个区间进行翻转操作,翻转操作实际上改变的就是先后关系。这启发我们对于普通平衡树做一些修改,改为依靠元素的前后关系建树,靠前的元素在左子树,靠后的元素在右子树,然后在区间翻转时维护这一性质,那么最后得到的中序遍历就是整个序列经过若干次区间翻转操作后的结果。
怎么做呢?首先我们有一个想法:假设裂出来的区间是 \([l,r]\),那么我们就在 FHQ-Treap 里把这一段直接分裂出来进行一些操作然后再合并回去。
怎么分裂出这棵子树来?首先我们知道,这个平衡树里维护的是节点的先后顺序而不是节点的大小,当我们翻转序列的时候,它显然就不满足二叉搜索树的兴致了,所以按照权值分裂不大行。
既然不能按权值分,那就按照子树的大小分,这也是一种经典的分裂途径。
这样分裂,简单来说,就是分出权值的效果,而又不需要权值。按大小分裂,就是把树拆成两棵树,其中一棵树的大小等于给定的大小,剩余部分在另一棵树里,因为我们维护的是先后顺序,所以我们要让它满足前一个树就是序列的前面的部分,后面的就是后面的部分。
给一个 UperFicial 的图。
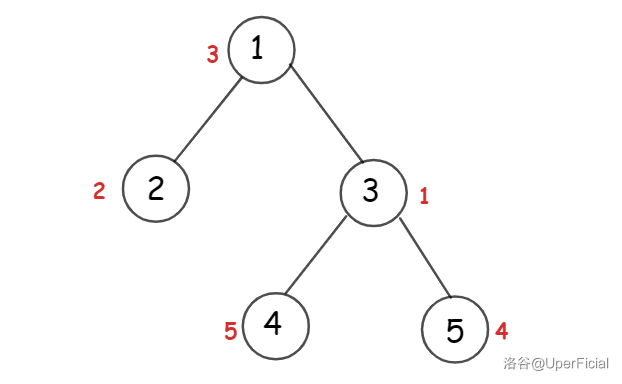
圈内是编号,红字代表节点的权值。
你可以看出,它显然不满足二叉搜索树的性质,因为为我们维护的是一个区间的中序遍历,此时这个区间就是 \(2-3-5-1-4\)。
我们知道,对于一个连续的区间,在这棵树中对应的节点也是相连的。那么我们就可以分裂两次,分别把区间左边和区间右边裂开,就能得到我们想要的区间。
我们先把整个树分解成 \([1,r]\) 和 \([r+1,n]\) 两个区间,然后再把 \([1,r]\) 分解成 \([1,l-1]\) 和 \([l,r]\) 这两个区间,我们就取出来了。
il void Split(int p,int k,int &x,int &y)//取前k个放在x,后面的放在y
{
if(!p) { x = y = 0; return ; }
push_down(p);//待会再说
if(k > tree[lc].size)//第k个在右子树
{
x = p;
Split(rc,k-tree[lc].size-1,rc,y);//类似于Get_Val函数的操作
push_up(x);
}
else
{
y = p;
Split(lc,k,x,lc);
push_up(y);
}
}
for(re int i=1;i<=m;i++)
{
l = read() , r = read();
int x,y,z;
Split(root,r,x,z);
Split(x,l-1,x,y);
tree[y].tag ^= 1;
root = Merge(Merge(x,y),z);
}
把区间找出来了,我们考虑应该进行什么样的操作。我们观察一下性质。
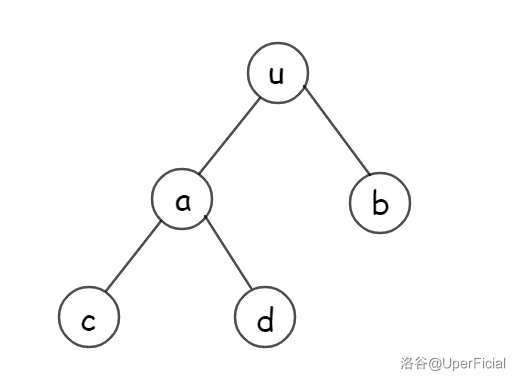
这是翻转前。
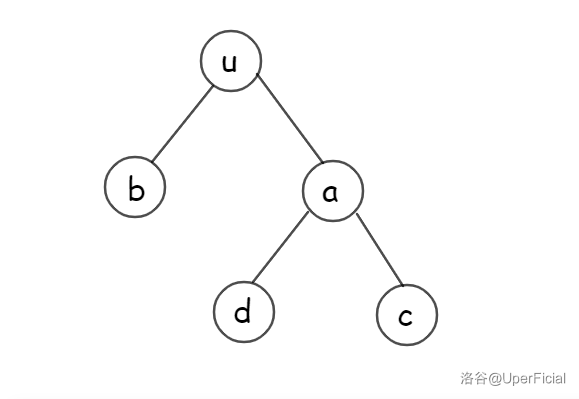
这是翻转后,我们观察一下我们干了个什么事,其实就是自上而下,把所有点的左右子树互换。我们可以暴力维护这个过程。但其实我们可以借用线段树懒标记的过程,\(tag=1\) 表明要取反,\(tag=0\) 表示不用取反。因为一个翻转的区间再翻转还是原区间,所以每次下放懒标记就 tag^=1 就可以了。
il void push_down(int p)
{
if(!tree[p].tag) return ;
swap(tree[p].l,tree[p].r);
tree[lc].tag ^= 1;
tree[rc].tag ^= 1;
tree[p].tag = 0;
}
而我们只需要给分裂出来的子树的根节点打上标记,再合并和最后输出答案的时候 pushdown 就行。
il int Merge(int x,int y)
{
if(!x || !y) return x | y;
if(tree[x].rnd < tree[y].rnd)
{
push_down(x);
tree[x].r = Merge(tree[x].r,y);
push_up(x);
return x;
}
else
{
push_down(y);
tree[y].l = Merge(x,tree[y].l);
push_up(y);
return y;
}
}
il void Print(int p)
{
if(!p) return ;
push_down(p);
Print(lc);
cout << tree[p].val << " ";
Print(rc);
}
最后贴上总代码,真的很短。code
Splay
不想写了,太丑了/qd。贴个代码。code


