线段树进阶拓展
前言
进军数据结构!
前置知识:权值线段树,但好像我这篇写的不咋地,所以建议网上搜一搜,其实会动态开点就行了,这个也很容易学。
这部分主要讲一讲线段树合并、线段树分裂、计算几何中的扫描线。
参考资料:
线段树合并
线段树合并常用于树上问题,因为合并过程本身就形成了一棵树。因为它比较常见也比较固定,所以应用空间较大。
概念
线段树合并,顾名思义,就是建立一棵新的线段树,这个线段树的每个节点都是两棵原线段树对应节点合并后的结果。它常常被用于维护树上或图上的信息。
显然,我们不能重新建立一棵新的满节点的线段树,这样的空间开销过大,而动态开点刚好就帮我们解决了这个问题。
线段树合并有两种方式:第一种方式是把一棵线段树合并到另一棵线段树上;第二种方式是把两棵线段树合并后建立一棵新树。
第二种方法的话空间开销比较大,所以我们应该采取动态开点。但当两棵线段树合并到其中一棵上,另一棵在后续的操作中没有用时,我们还是优先选择第一种方式,一来降低空间开销,二来好写。
过程
线段树合并的本质过程很暴力:
假设两颗线段树为 A 和 B,我们从一号节点开始递归合并。
-
递归到某个节点时,如果 A 树或者 B 树上的对应节点为空,直接返回另一个树上对应节点,意思就是其中有一个树是空的,那么合并后的树的这一部分其实原本就是两个树中不为空的那棵树的部分,所以直接加过来。
-
如果二者都不为空,我们递归到叶子节点,合并。
-
最后,根据子节点更新当前节点并返回。
//传址调用,Merge一次后就更新完了
il void Merge(int &x,int y,int l,int r)
{
if(!x || !y) x |= y;
else if(l == r)
{
//维护你要维护的信息
return ;
}
else
{
int mid = (l+r) >> 1;
Merge(tree[x].l,tree[y].l,l,mid);
Merge(tree[x].r,tree[y].r,mid+1,r);
push_up(x);
}
}
时间复杂度
引用 OI-Wiki 的分析:
显然,对于两颗满的线段树,合并操作的复杂度是 \(\mathcal O(n\log n)\) 的。但实际情况下使用的常常是权值线段树,总点数和 \(n\) 的规模相差并不大。并且合并时一般不会重复地合并某个线段树,所以我们最终增加的点数大致是 \(n\log n\) 级别的。这样,总的复杂度就是 \(\mathcal O(n\log n)\) 级别的。当然,在一些情况下,可并堆可能是更好的选择。
例题
P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并
这个题其实思路挺妙的。首先用差分把树上修改转化为单点修改。然后,我们对树上的每个节点都建立一个权值线段树,存储不同类型的救济粮的数量,然后最后一次 dfs 自底向上合并,把子节点的信息合并到父节点上。
虽然看起来复杂度很大,但是还是 \(\mathcal O(n\log n)\) 的复杂度。
然后有一个问题,就是我们的线段树要开多大。你会发现在每次差分修改的时候,最多会进行 \(\log n\) 次新建点,然后每次询问会有 \(4\) 次这种操作,一共 \(m\) 次,所以节点个数开到 \(4m\log n\) 即可,因为 \(n,m\) 同阶,所以就是 \(4n\log n\),开到 \(n \times 70\) 就足够。
线段树分裂
线段树分裂实质上是线段树合并的逆过程(从名字上你就能看出来),线段树分裂只适用于有序的序列,无序的序列没有意义。
相对线段树合并而言,线段树分裂的应用就不算太多了,具体遇到会再做补充。
线段树分裂有按值分裂和按排名分裂两种方法,这里只阐释按排名分裂。
过程
我们的目的是在一棵区间为 \([1,N]\) 的线段树中分裂出 \([l,r]\),建一棵新的树:
-
从 \(1\) 号节点开始递归分裂,当节点不存在或者代表的区间 \([nl,nr]\) 和 \([l,r]\) 没有交集时直接回溯(这里的 \(nl,nr\) 就代表现在递归到的区间)。
-
当 \([nl,nr]\) 和 \([l,r]\) 有交集时需要新开一个节点
-
当 \([l,r]\) 包含 \([nl,nr]\) 时,直接将当前节点接到新树下面,并把旧边断开。
il int Split(int nl,int nr,int l,int r,int &p)
{
int n = ++cnt;//返回根节点的编号,便于下次查询这个树
if(nl <= l && r <= nr)
{
tree[n] = tree[p];//直接接上去
p = 0;//并且把原边断掉
}
else
{
int mid = (l+r) >> 1;
if(nl <= mid) tree[n].l = Split(nl,nr,l,mid,tree[p].l);//递归找还需要断哪些部分
if(nr > mid) tree[n].r = Split(nl,nr,mid+1,r,tree[p].r);
push_up(p) , push_up(n);//更新原树和新树
}
return n;
}
时间复杂度
你会发现这个形式很像区间修改的形式,所以它的复杂度也是 \(\mathcal O(\log n)\) 的。
例题
其实挺板的,兼有线段树合并和线段树分裂,然后剩下三个操作就是朴实的单点修改,区间查询,和全局kth的模板。
同理分析一下该开多少空间,首先 Modify 里面会新建 \(\log n\) 个节点,Split 里面因为和区间修改类似,所以是 \(2\log n\),因为一次询问最多只能执行两种操作的一种,所以开 \(2\log n\) 就行了,那么就是 \(2m\log n\),差不多 \(n\times 40\) 左右,注意不要 define int long long,会 MLE。
扫描线
扫描线一般运用在图形上面,你通过它的算法名称可以想到,它就是一条线在整个图上左右或者上下移动,它一般被用来解决图形面积,周长,以及二位数点等问题。
接下来我们给出一个经典问题,也是洛谷模板题。
在二维坐标系上,给出 \(n\) 个矩形的左下以及右上坐标,求出所有矩形构成的图形的面积。\(n\leq 10^5\)。
试想,如果我们用一条竖直直线从左到右扫过整个坐标系,那么直线上被并集图形覆盖的长度只会在每个矩形的左右边界处发生变化。
也就是说,整个矩形被我们划分成 \(2n\) 段,每一段在直线上覆盖的长度(记为 \(L\))是固定的,因此该段的面积就是 \(L \times\) 该段的宽度,然后把各段面积之和相加即为答案。这条直线就被称为扫描线,这种解题思路就被称为扫描线法。
给个比较形象的图,摘自 OI-Wiki,不过它的扫描线是水平的,我接下来要写的是竖直的,但是本质上是一样的,可以了解一下过程。
流程
具体来说,我们可以取出 \(n\) 个矩形的左右边界。记矩形的左下角是 \((x_1,y_1)\),右上角是 \((x_2,y_2)\),就有 \(x_1<x_2,y_1<y_2\)。我们把矩形的左边界记为四元组 \((x_1,y_1,y_2,1)\),右边界记为 \((x_2,y_1,y_2,-1)\)。把这 \(2n\) 个四元组按照 \(x\) 递增排序,引用紫书上的图。
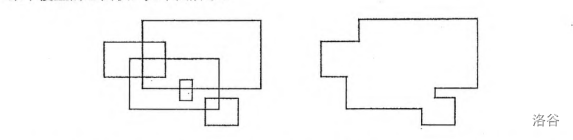
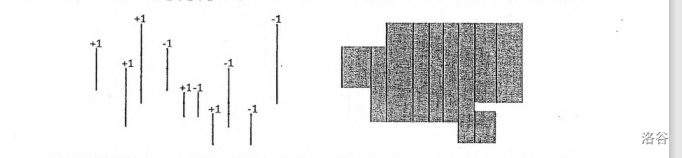
从这个图中我们看到,我们其实是在维护一个有效高度,有效高度就是区块内矩形的高度的并。每当扫到一个矩形的左边时,就加入该矩形高的贡献;而当扫到该矩形的右边时,就减去该矩形高的贡献。这个我们是通过四元组最后的 \(1\) 和 \(-1\) 来实现的。
因为 \(y < 10^9\),但是只有 \(10^5\) 个,所以我们要离散化。
我们先考虑暴力怎么做,我们把 \(y\) 离散化后,设 \(val(y)\) 表示 \(y\) 被离散化之后的值,\(raw(i)\) 就表示整数值 \(i\) 对应的原始 \(y\) 坐标值。
在离散化后,若有 \(m\) 个不同的 \(y\),分别对应 \(raw(1),raw(2),\dots, raw(m)\),则扫描线会被切成 \(m-1\) 段,其中第 \(i\) 段区间为 \([raw(i),raw(i+1)]\)。我们给定一个数组 \(c\),用 \(c_i\) 记录扫描线上第 \(i\) 段被覆盖的次数。初值为 \(0\)。
逐一扫描排序后的 \(2n\) 个四元组,设当前四元组为 \((x,y_1,y_2,k)\),我们把数组 \(c\) 中的 \(c[val(y_1)],c[val(y_1)+1],\dots,c[val(y_2)-1]\) 这些值都加上 \(k\),相当于覆盖了 \([y_1,y_2]\) 这个区间。此时,如果下一个四元组的横坐标为 \(x_2\),那么扫描线从 \(x\) 扫到 \(x_2\) 的过程中,被覆盖的长度就是 \(\displaystyle \sum_{c_i>0}(raw(i+1)-raw(i))\),即 \(c\) 数组中至少被覆盖一次的段的总长度,我们就让最终的答案 \(ans\) 加上 \(\displaystyle (x_2-x) \times \sum_{c_i>0}(raw(i+1)-raw(i))\)。
对于每个四元组,我们暴力修改加查询,时间复杂度是 \(\mathcal O(n^2)\) 的。
而正解就是采用离散线段树维护的这些信息。
值得一提的是,四元组上的 \(y_1,y_2\) 都是坐标,是一个点。而我们需要维护的是扫描线上每一段被覆盖的次数及其长度,所以我们维护点的信息是没有意义的,所以离散线段树实际上维护的信息其实是一个区间,这样的特点让他的建树并不是 \([l,mid],[mid+1,r]\),而是 \([l,mid],[mid,r]\),具体给个董晓老师的图理解一下。

首先是区间边界的不同,如我上面所说;再一个是叶子节点的不同,维护一个点没有意义,所以叶子节点的宽度是 \(2\),代表着一个区间。这样的特点使得这样的线段树便于维护坐标值、区间长度。
在本题中,我们只关心根节点上被矩形覆盖的长度,而且区间修改也是成对出现的 (\(1\) 和 \(-1\))。所以不需要懒标记,直接做就行。
我们在线段树中维护这个点的 \(raw(l),raw(r)\),以及被矩形覆盖的长度和被矩形覆盖的次数。
对于一个四元组 \((x,y_1,y_2,k)\),我们执行区间修改操作,给个代码理解一下。
il void push_up(int p)
{
if(tree[p].cnt) tree[p].val = tree[p].r - tree[p].l;//被覆盖了直接就是自己的区间长度
else tree[p].val = tree[lc].val + tree[rc].val;//否则就是儿子的加起来
}
il void Modify(int p,int nl,int nr,int c)
{
if(nr <= tree[p].l || tree[p].r <= nl) return ;//当前节点的左右边界和给定区间的左右边界没有交集
if(nl <= tree[p].l && tree[p].r <= nr)//当前节点被给定区间完全包含
{
tree[p].cnt += c;//修改操作次数
push_up(p);
return ;
}
Modify(lc,nl,nr,c) , Modify(rc,nl,nr,c);
push_up(p);
}
就是这么一个递归过程,如果无交,那么直接返回;如果被全部覆盖,那么直接计算贡献;如果有交集但不包含,再递归往下找。
我们看看计算贡献是怎么计算的:如果当前节点的覆盖次数 \(>1\),直接利用自己计算长度,这说明这个区间是至少被一个矩形覆盖住的,那我们加上长度就行了,不用再往下找;如果覆盖次数 \(=0\),说明它并没有被任何一个矩形完全包含,但是它的子区间可能被完全包含,所以计算它的贡献就是利用它的子区间进行求和。
这样,我们区间修改的复杂度就从 \(\mathcal O(n)\) 变成了 \(\mathcal O(\log n)\),总复杂度就变成了 \(\mathcal O(n\log n)\),可以通过。
其实本质上就是利用线段树维护区间信息,由于和普通的维护点的信息的线段树不大一样,所以要注意好边界。
并且需要注意的是,由于 tree[p].val = tree[lc].val + tree[rc].val; 这一句代码的存在,它会访问叶子节点的子节点,这就需要我们,开 \(8\) 倍空间,才能避免 RE。
这就是扫描线的基本内容了,如果你想了解的更透彻,推荐跟着董晓老师的扫描线视频走一遍流程,理解应该会更加深入。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号