动态规划（Ⅲ）

前言

这部分主要讲一讲 DP 优化的一些方法，显然我的实力不太够，所以只能写一些比较简单的东西。

如动态规划（Ⅰ）中提到的，动态规划的优化一般就可以从两个方面入手：一个是状态表示、另一个是决策集合，也就是状态转移的角度来优化。下文主要就是分别从这两个角度，阐述不同的 DP 优化方法。

倍增优化 DP

倍增优化 DP，是从状态表示的方面来进行 DP 优化。简单来说，因为动态规划经常采用按阶段的递推形式实现，所以也可以按照类似的方法，使用倍增把阶段的线性增长优化为成倍增长，也就是把一段 $\mathcal O(n)$ 的部分优化成 $\mathcal O(\log n)$，显然，优化效果显著。

下面给一道例题来讲一下倍增优化 DP 的方式。

例题

P1081 [NOIP2012 提高组] 开车旅行

题面太长了就不放了。

这道题 $70$ 分代码是比较好写的，建议先写一下 $70$ 分的 $\mathcal O(n^2)$ 做法：

维护四个数组 $city_1[i],city_2[i],dis_1[i],dis_2[i]$，分别表示距离城市 $i$ 最近的城市，次近的城市，以及它们分别到城市 $i$ 的距离。我们朴素地暴力 $\mathcal O(n^2)$ 便能解决这个问题。

然后对于两个问题，我们便运用这四个数组，$O(nm)$ 的枚举即可，没啥难度。
code

然后我们考虑怎么优化，其实这个题我感觉不像是一个真正的 DP，因为你一旦确定了起点，其实你的路径就是固定的了，而正是因为这个性质，使得我们可以采用倍增的方法来优化我们的复杂度。

倍增优化 DP

想要倍增优化，我们就考虑我们想知道什么：行驶到了哪座城市、小 A 行驶的路程、小 B 行驶的路程。根据这个，我们设出倍增 DP 的数组：

下文中，$k=0$ 代表小 A 开车，$k=1$ 代表小 B 开车。

设 $f_{i,j,k}$ 表示从城市 $j$ 出发，行驶 $2^i$ 天，$k$ 先开车，最终会到达的城市；

设 $da_{i,j,k}$ 表示从城市 $j$ 出发，行驶 $2^i$ 天，$k$ 先开车，小 A 行驶的路程；

设 $db_{i,j,k}$ 表示从城市 $j$ 出发，行驶 $2^i$ 天，$k$ 先开车，小 B 行驶的路程。

假设我们已经知道了暴力解法中的四个数组的值，我们考虑怎么求倍增数组。

初值的设定：

f[0][i][0] = city2[i], f[0][i][1] = city1[i];
da[0][i][0] = dis2[i], da[0][i][1] = 0;
db[0][i][0] = 0 ,db[0][i][1] = dis1[i];

结合数组意义应该不难看懂，接下来，我们按照预处理倍增数组的一般思路，递增第一维。

需要注意的是，当 $i=1$ 时，我们从 $i=0$ 扩展而来，这时候司机是变了一个人的；而当 $i>1$ 时，我们从 $i-1$ 转移而来，这时第 $2^i$ 天和 $2^{i-1}$ 天都是偶数，是由同一个人转移而来，所以要分类讨论一下。

当 $i=1$ 时：

f[1][j][k] = f[0][f[0][j][k]][k ^ 1];
da[1][j][k] = da[0][j][k] + da[0][f[0][j][k]][k ^ 1];
db[1][j][k] = db[0][j][k] + db[0][f[0][j][k]][k ^ 1];

当 $i>1$ 时：

f[i][j][k] = f[i - 1][f[i - 1][j][k]][k];
da[i][j][k] = da[i - 1][j][k] + da[i - 1][f[i - 1][j][k]][k];
db[i][j][k] = db[i - 1][j][k] + db[i - 1][f[i - 1][j][k]][k];

求解问题

朴素的求解问题是一步一步模拟走过的城市。有了倍增数组后，我们自然就可以进行倍增跳步了。具体实现如下：

我们给定 $pos=0,disA = 0 ,disB= 0$，分别表示现在在哪个城市，小 A 的路程，小 B 的路程。
令 $i$ 从 $\log n$ 枚举到 $0$，判断 $f_{i,pos,0}$ 是否越界，并且 $disA + disB + da_{i,pos,0} + db_{i,pos,0} \leq x$ 是否成立。如果不越界且成立，那么就直接令 $pos=f_{i,pos,0},disA += da_{i,pos,0},disB += db_{i,pos,0}$，这也就实现了我们的跳步操作。

第二步结束后，$disA$ 和 $disB$ 就可以求出来了，有了这个，问题 $1,2$ 就都很好解决了，我们就可以在 $\mathcal O(n\log n)$ 的时间下解决问题。

dis = disA = disB = 0 , pos = i;
for(re int j=18;j>=0;j--)
{
	if(f[j][pos][0] != n+1 && disA + disB + da[j][pos][0] + db[j][pos][0] <= x)
	{
		disA += da[j][pos][0];
		disB += db[j][pos][0];
		pos = f[j][pos][0];
	}
}

解决根源的初始化

其实我们发现，我们还漏了一个地方，也就是那四个数组的初始化其实还是 $\mathcal O(n^2)$ 的，但因为这个地方的优化跟倍增没有关系，所以放到最后来说。

具体来说，我们维护一个 multiset，存储节点编号和节点高度，初始时我们插入 $4$ 个边界，两个 $-\inf$，两个 $\inf$，然后我们从右向左将每个城市插入进去，然后利用 multiset $\mathcal O(\log n)$ 的查询它的前驱，前驱的前驱，后继，后继的后继，然后取一个最小值和次小值即可。（multiset 里面按高度从小到大排序）。

这样一来，初始化也是 $\mathcal O(n\log n)$ 的了，综上，我们运用倍增优化 DP，就在 $\mathcal O((n+m)\log n)$ 解决了这个问题。

code

此外的例题还有 AcWing294.计算重复，这里有两种倍增的手法，但其中一种更为优秀，具体可以看第一篇题解。

总结

倍增优化 DP 其实感觉不怎么像是 DP，因为能使用倍增 DP 的前提是，每个路线是已经确定的了，是静态的。当然这其中也有 DP 的思想，因为我们设的倍增数组其实就是 DP 的体现。

数据结构优化 DP

倍增 DP 是从状态表示入手，对 DP 进行的优化，而状压 DP 虽然称不上是一种优化，但他同样也是从状态表示出发，进行的 DP。

当状态表示和状态转移方程确定后，我们的主要问题就是如何优化我们的转移。

在前文中我们提到，在实现状态转移方程时，要注意观察决策集合的范围随着状态的变化情况。对于“决策集合中的元素只增加不减少”的情景，就可以只用一个变量维护最值，不断与新加入的集合元素比较，即可得到最优决策，从而 $O(1)$ 地转移。

但是在更复杂的情况下，我们就要用更加高级的数据结构（而不是一个小小的变量）维护 DP 决策的候选集合，以便快速执行插入元素、删除元素，查询最值等操作，把朴素的暴力枚举时间降到维护数据结构的时间，这就是数据结构优化 DP 的意义。

例题

P4644 [USACO05DEC] Cleaning Shifts S

有一个很长的纸条，被分成了若干长度为 $1$ 的小纸条。其中从第 $L$ 个到第 $R$ 个纸条被污染了。$N$ 个贴纸。每个贴纸能覆盖的区间是 $[S_i,E_i]$，售价为 $c_i$，问最少需要多少钱能把这个区间覆盖。无解输出 $-1$。

$0\leq L\leq R \leq 86399,N\le 10^4,L \le S_i\le E_i\le R,0 \leq c_i \leq 5 \times 10^5$

我们先判断我们要维护什么信息：覆盖的区间，覆盖的花费，可以看出，这个题的阶段就是覆盖的区间，状态就是区间 + 花费。

我们设 $f_i$ 表示覆盖 $[L,i]$ 这个区间所需要的最小花费。

为了便于转移，我们将每个人按照右端点 $E_i$ 递增排序，那么有状态转移方程：

\[f_{E_i} = \min_{S_i-1\leq x < E_i}\{f_x\} + c_i \]

其实就是枚举是否能接起来，覆盖区间必须有交或者刚好相邻。

那我们就可以进行 DP 了，初值 $f_0= 0$，其余为 $\inf$。最终答案就是 $f_T$。

设 $|S| = R-L$，那么朴素 DP 是 $\mathcal O(N|S|)$ 的，我们考虑怎么优化。

我们观察状态转移方程，发现这其实是一个查询区间最小值的操作，并且会有修改操作，因为 $f$ 是在不断更新的。我们很自然的就能想出用线段树来解决这个问题，这样我们就可以在 $\mathcal O(\log |S|)$ 的时间内完成这个问题。时间复杂度 $\mathcal O(N\log |S|)$。

需要注意的一点是，我们是在 $[L-1,R]$ 上建立的线段树而并非 $[L,R]$，因为状态转移方程中左端点是 $S_i-1$。

同时，我们可以将整个区间左移 $L-1$，这样 $L=1$，比较清晰一点。

#include<bits/stdc++.h>
#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e6 + 5;
const int INF = 1e11;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

int n,R;
int f[N];
struct node{
	int l,r;
	int cost;
}a[N];
int tree[N<<2];

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

#define lc p<<1
#define rc p<<1|1

il void build(int p,int l,int r)
{
	if(l == r)
	{
		tree[p] = INF;
		return ;
	}
	int mid = (l+r) >> 1;
	build(lc,l,mid) , build(rc,mid+1,r);
	tree[p] = min(tree[lc],tree[rc]);
}

il void Modify(int pos,int l,int r,int p,int k)
{
	if(l == pos && r == pos)
	{
		tree[p] = k;
		return ;
	}
	int mid = (l+r) >> 1;
	if(pos <= mid) Modify(pos,l,mid,lc,k);
	if(pos > mid) Modify(pos,mid+1,r,rc,k);
	tree[p] = min(tree[lc],tree[rc]);
}

il int Query(int nl,int nr,int l,int r,int p)
{
	int ans = INF;
	if(nl <= l && r <= nr) return tree[p];
	int mid = (l+r) >> 1;
	if(nl <= mid) ans = min(ans,Query(nl,nr,l,mid,lc));
	if(nr > mid) ans = min(ans,Query(nl,nr,mid+1,r,rc));
	return ans;
}

il bool cmp(node a,node b) { return a.r < b.r; }

signed main()
{
	n = read() , R = read();
	for(re int i=1;i<=n;i++)
	{
		a[i].l = read() , a[i].r = read();
		a[i].cost = 1;
	}
	sort(a+1,a+n+1,cmp);
	build(1,0,R);
	Modify(0,0,R,1,0);
	for(re int i=1;i<=R;i++) f[i] = INF;
	f[0] = 0;
	for(re int i=1;i<=n;i++)
	{
		int Min = Query(a[i].l-1,a[i].r-1,0,R,1);
		f[a[i].r] = min(f[a[i].r],Min + a[i].cost);
		Modify(a[i].r,0,R,1,f[a[i].r]);
	}
	if(f[R] == INF) cout << -1; else cout << f[R];
	return 0;
}

UVA12983 The Battle of Chibi

$T$ 组数据，在长度为 $n$ 的数列 $a$ 中，求出长度为 $m$ 的严格上升子序列的个数。答案对 $10^9 + 7$ 取模。

$1\leq m \leq n \leq 1000,1\leq a_i \leq 10^9,1\leq T \leq 100$

LIS 计数问题。我们先考虑我们之前学过的 LIS 问题。

在 LIS 问题中，我们存在 $\mathcal O(n^2)$ 的朴素解法，也有贪心+二分的 $\mathcal O(n\log n)$ 和树状数组优化的 $\mathcal O(n\log n)$ 解法。其中，朴素枚举太慢，二分+贪心的思路在计数问题中就显得困难，而树状数组优化就显现出了优越性。我们将在下文中，讲讲为什么可以用树状数组。

首先对于 LIS 计数，我们先从朴素出发：设 $f_{i,j}$ 表示考虑到了前 $i$ 个数并且以 $a_i$ 结尾的数列中，长度为 $j$ 的严格上升子序列有多少个，显然有状态转移方程：

\[f_{i,j} = \sum_{k<i\text{且}a_k < a_i} f_{k,j-1} \]

我们可以写出代码来看一看。

a[0] = 0 , f[0][0] = 1;
for(re int j=1;j<=m;j++)//枚举长度
	for(re int i=1;i<=n;i++)
		for(re int k=0;k<i;k++)//决策集合
       		 if(a[k] < a[i])
				f[i][j] = (f[i][j] + f[k][j-1]) % mod;

我们发现，在内层循环 $i$ 和 $k$ 转移的时候，外层循环 $j$ 是个定值。我们又发现，当 $i$ 增加 $1$ 时，$k$ 的取值范围从 $0\leq k < i$ 变成了 $0 \leq k < i+1$，也就是只多了一个决策点。所以，我们需要维护一个决策候选集合，其中每个决策可以用一个二元组 $(a_k,f_{k,j-1})$ 来表示。

1. 插入一个新的决策。在 $i$ 自增 $1$ 之前，把 $(a_i,f_{i,j-1})$ 加入决策候选集合。
1. 给定一个 $a_i$ 查询所有 $a_k < a_i$ 的 $f_{k,j-1}$ 的和。

如果把 $a_i$ 当作编号，$f_{i,j-1}$ 当作权值，你会发现这就是一个单点更新，区间求和的数据结构，于是，我们能很自然的想到用树状数组来维护。这个维护的过程其实和树状数组求逆序对的过程很类似。插入决策前，我们就在 $a_i$ 的位置上插入 $f_{i,j-1}$，在查询的时候，对区间 $[0,a_i-1]$，在树状数组求一个前缀和即可。这样，整个算法的复杂度就从 $\mathcal O(n^2m)$ 变成了 $\mathcal O(nm\log n)$。

此外要注意的是，$a_i$ 的值域很大，而这个题我们并不关心 $a_i$ 的值具体是多少，只关心它们的相对大小，所以离散化一下即可。

il int lowbit(int x) { return x&(-x); }

il void add(int x,int k) { for(;x<=len;x+=lowbit(x)) BIT[x] = (BIT[x]+k) % mod; }

il int Query(int x) { int res=0; for(;x;x-=lowbit(x)) res = (res+BIT[x]) % mod; return res; }

signed main()
{
	n = read() , m = read();
	for(re int i=1;i<=n;i++) a[i] = read() , b[i] = a[i] , f[i][1] = 1;
	sort(b+1,b+n+1);
	len = unique(b+1,b+n+1) - b - 1;
	for(re int i=1;i<=n;i++) a[i] = lower_bound(b+1,b+len+1,a[i]) - b;//离散化
	for(re int j=2;j<=m;j++)
	{
		memset(BIT , 0 , sizeof BIT);
     //因为树状数组中存储的其实是f_{i,j-1}，所以对于一个新的 $j$
     //要注意清空 BIT 数组
		for(re int i=1;i<=n;i++)
		{
			f[i][j] = Query(a[i]-1);//前缀和
			add(a[i],f[i][j-1]);//加入决策集合
		}
	}
   for(re int i=1;i<=n;i++) ans = (ans + f[i][m]) % mod;
   cout << ans;
}

总结

在不同的问题中，我们采用了不同的方法去维护。当决策集合只增不减时，我们运用一个变量去解题；在第一个例题中，右端点递增，但左端点没有什么明显的性质，我们采用了数据结构去维护；在第二个例题中，取值范围有两个限制：数组下标以及 $a$ 的值，我们在枚举的过程中保证了数组下标的递增，对于 $a$ 值，我们采用了树状数组去维护，这其实就是我们在数列 $a$ 这个坐标轴上建立了以 $f$ 数组中的状态为值的数据结构。

在不同的题目中，我们往往需要根据题目的情况，来判断我们需要什么，应该运用什么样的数据结构。题目千变万化，但是我们有一个优化的大致思路：也就是考虑状态转移的决策集合的变化情况，从而考虑如何去优化它的转移。

单调队列优化 DP($t$D/$e$D)

单调队列，本质上也是一种数据结构。但是因为它跟线段树、树状数组、平衡树那类数据结构优化 DP 的方式不完全一样，所以把它单独拿出来说说。

适用情况

单调栈和单调队列两种数据结构，本质上都是借助单调性，及时排除不可能的决策，保持候选集合答案的有效性和有序性。我们先用一个例子来引入：

最大子序和

我们将问题转化成前缀和后，容易发现问题转化成了一种类似于 DP 的形式：

\[ans = \max_{1\leq i\leq n}\{sum_i - \min_{i-m\leq j \leq i-1}\{sum_j\}\} \]

朴素计算时，我们枚举 $i,j$，是一个 $\mathcal O(nm)$ 的算法。但，我们观察一下它的性质：

当 $i$ 增大 $1$ 时，$j$ 的取值范围同时 $+1$，由 $[i-m,i-1]$ 变为 $[i-m+1,i]$。这意味着不仅有一个新的决策 $j=i$ 进入决策候选集合，也应该把旧的 $j=i-m$ 的决策从决策集合中删除。你会发现这非常适合用单调队列来维护，因为单调队列就适用于维护决策取值范围的上下界均单调变化，每个决策在候选集合中插入或删除至多一次的问题，在这个问题中，我们用单调队列维护最小值，便可以让转移变为均摊 $\mathcal O(1)$，最后的复杂度就是 $\mathcal O(n)$。

接下来我们给出例题。

例题

POJ1281 Fence

$n$ 块木板从左到右排成一行，有 $m$ 个工匠对这些木板进行粉刷，每块木板至多被粉刷一次。第 $i$ 个工匠要么不刷，要么刷包含木板 $s_i$ 的、长度不超过 $L_i$ 的一段连续的木板，每粉刷一块可以得到 $p_i$ 的报酬，问如何安排能够使工匠们获得的总报酬最大。$1\leq n \leq 16000,1\leq m \leq 100$。

首先手玩一下你会发现，$s_i$ 靠后的刷的范围一定在 $s_i$ 靠前的人的刷的范围之后，这样才能保证最大化收益。所以我们先对所有的工匠按照 $s_i$ 从小到大排序，这样我们就能进行线性 DP 了。

观察我们描述一个状态需要什么：用了几个工匠，刷了多少板子。利用这两个信息，我们便可以描述一个状态了。

设 $f(i,j)$ 表示考虑到前 $i$ 个人，它们刷了前 $j$ 块木板（注意，有的地方可能不刷），工匠能获得的最高报酬，我们把这个集合划分一下。

首先第 $i$ 个人可刷可不刷，如果不刷，$f(i,j) = f(i-1,j)$；
如果他刷，再考虑第 $j$ 个木板刷不刷，如果不刷，$f(i,j) = f(i,j-1)$；
如果它刷第 $j$ 个木板，需要满足一些条件：假设它刷的是第 $k+1$ 到第 $j$ 块木板。那么，我们要保证 $j-k \leq L_i$ 并且 $k+1 \leq s_i \leq j$，这样才能转移，于是有状态转移方程：

\[f(i,j) = \max_{j-L_i \leq k \leq s_i-1}\{f(i-1,k)+p_i \times (j-k)\} \]

这个题的重难点就在这，前两个转移都很好转移，我们重点考虑这个。

首先，朴素转移的时间复杂度是 $\mathcal O(n^2m)$ 的，不大优秀。这就需要我们观察一些性质来去优化，通过观察，我们能发现的性质有：

当外层循环 $i$ 不变时，若 $j$ 增加 $1$，那么决策集合，也就是 $k$ 的取值范围就由 $[j-L_i,s_i-1]$ 变为 $[j-L_i+1,s_i-1]$，也就是上界不变，下界增加。
在 $j$ 不变时，$p_i \times j$ 其实是不变的，可以把它从 $\max$ 中提取出来，式子变成：

\[ f(i,j) = p_i \times j + \max_{j-L_i \leq k \leq s_i-1}\{f(i-1,k)-p_i \times k\} \]

因为上界不变，下界递增，我们可以考虑运用单调队列维护，维护的信息就是这个 $\max$ 里的最大值，同时当 $j$ 增加 $1$ 的时候，把过时的 $j-L_i$ 踢出决策；同时，若 $j<s_i$，也就是 $j$ 能新加入决策集合的时候，把它加到决策集合里，而若 $j\geq s_i$ 了，它就不符合 $k$ 的范围了，就不加进去了。这样，当 $i$ 恒定时，每个元素至多进队出队一次，转移的复杂度就是均摊 $\mathcal O(1)$ 的，这样总复杂度就是 $\mathcal O(nm)$ 的，可以通过。

int n,m;
int f[M][N];
int head,tail,q[N];
struct node{
	int l,p,s;
	friend bool operator < (const node &a,const node &b) {
		return a.s < b.s;
	}
}a[N];

signed main()
{
	n = read() , m = read();
	for(re int i=1;i<=m;i++) a[i].l = read() , a[i].p = read() , a[i].s = read();
	sort(a+1,a+m+1);//f[i][j] 表示考虑到了前i个人和考虑到了前j个板子的情况
	for(re int i=1;i<=m;i++)
	{
		head = 1 , tail = 0;
		int l = a[i].l , p = a[i].p , s = a[i].s;
		for(re int j=0;j<=n;j++)
		{
			f[i][j] = f[i-1][j];
			if(j) f[i][j] = max(f[i][j],f[i][j-1]);//注意j的范围
			while(head <= tail && q[head] < j - l) head++;//删队头
			if(head <= tail && j >= s && q[head] >= j - l) f[i][j] = max(f[i][j],f[i-1][q[head]] + p * (j-q[head]));//取最值
			if(j < s)//能加才加
			{
				while(head <= tail && f[i-1][q[tail]] - p * q[tail] <= f[i-1][j] - p * j) tail--;
				q[++tail] = j;
			}
		}
	}
	cout << f[m][n];
}

还有很多习题，下面给出几个：

P1848 [USACO12OPEN] Bookshelf G：一个不是很具有普适性的单调队列优化 DP
P2254 [NOI2005] 瑰丽华尔兹
P2569 [SCOI2010] 股票交易

单调队列优化多重背包

推荐观看视频：多重背包单调队列优化 - 董晓算法。

这里就不细讲了，具体原理就是 $f$ 数组是按类进行更新的，所以可以把 $f[0\sim m]$ 按体积 $w$ 分成 $w$ 个类。

因为多重背包的转移式是

\[f_j = \max(f_j,f_{j-k\times w} + k\times v) \]

所以说 $f_j$ 只能由 $f_{j-w},f_{j-2w},f_{j-cw}$ 转移而来，$c$ 就是这个物品的个数，所以看出来这其实是一个组，把每个组分开考虑，运用单调队列维护队头和队尾。这样每次每个数只会进队出队最多一次，复杂度就是 $\mathcal O(nm)$，是最优的了。

for(re int i=1;i<=n;i++)
{
	memcpy(g , f , sizeof f);//其实就是把f[i-1][j]的状态存到 g 里，当然你也可以用滚动数组
	v = read() , w = read() , c = read();
	for(re int j=0;j<w;j++)
   {
		int head = 1 , tail = 0;
		for(re int k=j;k<=m;k+=w)
		{
			while(head <= tail && q[head] < k - c * w) head++;//判断越界否，就是说f[k]能否由q[head]这部分转移而来
        //如果个数差太大，就删掉
			if(head <= tail) f[k] = max(g[k],g[q[head]]+(k-q[head])/w*v);//k-q[head]/w就表明选了几个
			while(head <= tail && g[k] >= g[q[tail]]+(k-q[tail])/w*v) tail--;//其实省略了(k-k)/w*v，因为是0，所以就不用写上去了
			q[++tail] = k;
		}
	}
}

总结

给张图：

我们发现，只关注“状态变量”和“决策变量”及其所在的维度，这些状态转移方程都可以大致归类成如下的形式：

\[f_i = \min_{L(i)\leq j \leq R(i)}\{f_j + val(i,j)\} \]

这个式子所代表的问题覆盖范围广泛，是一个重要的 DP 模型。我们可以看出，这个式子其实是 $1D/1D$ 的，朴素显然是 $\mathcal O(n^2)$，但既然我们是从单调队列优化 DP 总结出来的，说明如果这个式子里面的某些值具有某些性质，那么我们就可以优化复杂度。

$L(i),R(i)$ 是关于变量 $i$ 的一次函数，用来限制决策 $j$ 的取值范围，并保证上下界的变化具有单调性；
$val(i,j)$ 是一个关于变量 $i,j$ 的多项式函数，在例题中，我们都是把 $val(i,j)$ 分成两部分，第一部分仅与 $i$ 有关，第二部分仅与 $j$ 有关。当 $i$ 不变时，我们把第一部分抽出来，这一部分值是不变的，变化的只是第二部分。于是，我们就可以在队列中维护第二部分的单调性，及时排除不优秀的决策，让 DP 复杂度得以优化。

所以，在这种模型中，边界具有单调性，且多项式 $val(i,j)$ 的每一项仅与 $i$ 和 $j$ 中的一个有关，是使用单调队列进行优化的基本条件。

斜率优化(1D)

梦回去年暑假。

在单调队列优化 DP 中，我们给出了 DP 的一个经典模型

\[f_i = \min_{L(i)\leq j \leq R(i)}\{f_j + val(i,j)\} \]

并且，我们总结了单调队列优化这种形式的 DP 的基本条件：边界具有单调性，且多项式 $val(i,j)$ 的每一项仅与 $i$ 和 $j$ 中的一个有关。而在斜率优化中，我们将讨论多项式 $val(i,j)$ 包含 $i,j$ 的乘积项，即存在一个同时与 $i$ 和 $j$ 有关的部分时，该如何进行优化。

建议在阅读本部分前你有一定的计算几何基础，没有也完全没有关系，只是辅助理解而已。

例题

HDU3507 Print Article

Zero 要打印一个有 $N$ 个单词的文章，每个单词 $i$ 的打印成本为 $C_i$。在一行中打印 $k$ 个单词的成本为 $\displaystyle (\sum_{i=1}^kC_i)^2 +M$，$M$ 是一个常量。他想知道打印文章的最小成本。$1\leq N \leq 5 \times 10^5,1\leq M\leq 1000$

可以看出，这是一个典型的线性 DP，为了优化掉这个 $\sum$，我们可以做一个 $C_i$ 的前缀和，记作 $s_i$，我们设 $f_i$ 表示打印前 $i$ 个单词的最小成本，那么有很显然的状态转移方程：

\[f_i = \min_{0\leq j\leq i-1}\{f_j+(s_i-s_j)^2+m\} \]

我们要把这个状态转移方程稍作变形，先把 $\min$ 函数去掉。

\[f_i = f_j+s_i^2-2s_is_j+s_j^2+m \]

把常数、仅与 $i$ 有关的项、仅与 $j$ 有关的项，以及 $i,j$ 的乘积项分开。本着在这次决策中，$i$ 是不变的，所以我们把含 $j$ 项看作变量，含 $i$ 项看作常量。

\[f_j + s_j^2 = 2s_is_j + (f_i-s_i^2-m) \]

我们对比一下直线解析式 $y=kx+b$，你会发现

\[y = f_j + s_j^2\ ,\ x=s_j \ , \ k = 2s_i \ , \ b = f_i - s_i^2 - m \]

我们可以看出，当 $j$ 不同时，$(x,y)$ 就对应着平面上不同的点。

我们明确我们的目标：我们想找到一个 $j$，使得 $f_i$ 最小，而此时，$i$ 是确定的，也就是 $k$ 是确定的，所以我们就想让截距 $b$ 最小，如果 $b$ 最小了，$f_i$ 就是最小的。

因此，我们目的就是找一个 $(x,y)$，使得 $y=kx+b$ 中的 $b$ 最小。接下来我们的目标就转化为了怎么去找这个 $(x,y)$，给个图。

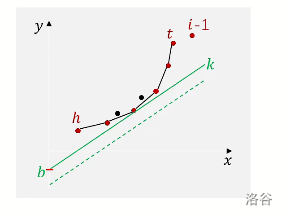
我们发现，这个找 $(x,y)$ 的过程其实就是一条斜率为 $k$ 的直线从下往上平移，直到经过了一个点的过程，这个点就是我们要找的 $(x,y)$，因为这条直线向上移动的距离是整个决策集合中最短的，也就是 $b$ 是最小的，那么这个点对应的 $j$，就是我们要利用进行转移的。

然后你观察一下，所有可能被利用进行转移的 $(x,y)$，一定在决策集合的 $(x,y)$ 构成的下凸壳上，如果不在下凸壳上，那么一定有比它更小的点能先被找到，所以这其实是一个维护下凸壳的过程，维护下凸壳我们可以用单调队列来实现，这就是斜率优化所在的点：它即使排除掉了不可能的决策，使得转移是均摊 $\mathcal O(1)$ 的。

接下来我们再来看如何去找到这个点。

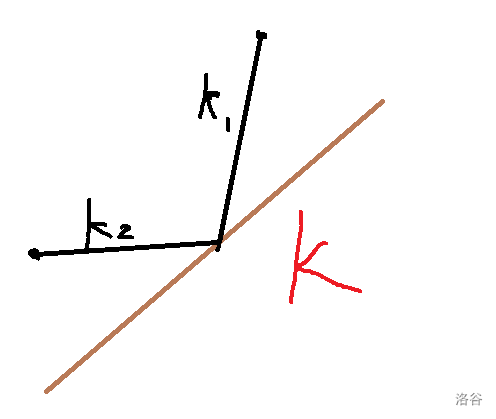
观察这个图，假设这个点和下凸壳上的其余两个点构成的直线的斜率分别是 $k_1,k_2$，那么我们发现如果 $k_2 \leq k \leq k_1$，那么这个点就是我们要找的决策点，$k_1,k_2$ 也很好求，运用斜率公式 $\displaystyle \frac{y_i-y_j}{x_i-x_j}$ 求一下就行了。

我们再看一下这个题，其中当 $i$ 增加时，斜率 $k$ 也是单调递增的，假设我们在这次循环的时候找到了最优决策点 $j$，那么凸包中在 $j$ 左侧的点在 $i$ 变大后，一定不会被选上，有可能被选上的只有在 $j$ 右边的点，所以我们同时要维护一下队头。

至此，我们整理一下思路。

1. 若新点 $i-1$ 与队尾点连线的斜率 $\leq$ 队尾邻点直线的斜率，则队尾出队，实际上是一个维护下凸壳的过程。

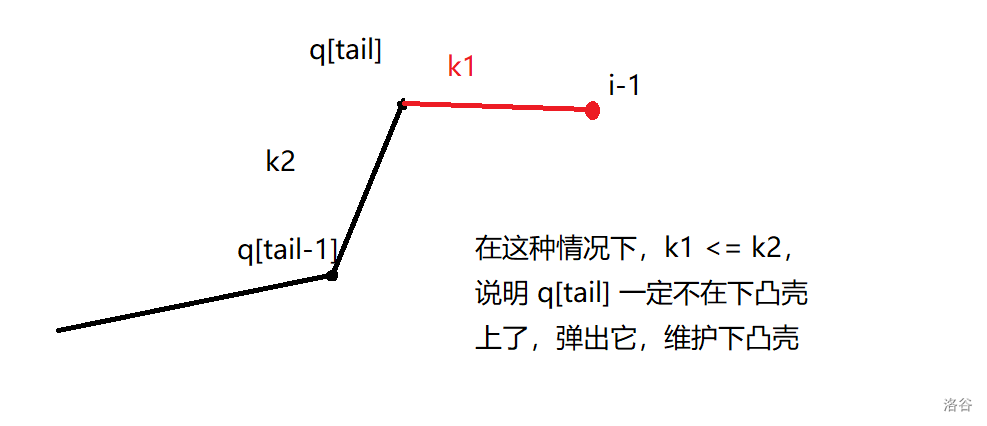
1. 新点 $i-1$ 入队
1. 若队头邻点直线的斜率 $\leq k_i$，则队头出队，删除不可能被选上的点。
1. 此时队头就是最优决策点，做状态转移。

这其中有一个化除为乘的 trick，也就是求斜率的时候把

\[\frac{\Delta y_{i-1,q_{tail}}}{\Delta x_{i-1,q_{tail}}} \leq \frac{\Delta y_{q_{tail},q_{tail-1}}}{\Delta x_{q_{tail},q_{tail-1}}} \]

变成

\[\Delta y_{i-1,q_{tail}}\Delta x_{q_{tail},q_{tail-1}} \leq \Delta y_{q_{tail},q_{tail-1}}\Delta x_{i-1,q_{tail}} \]

这样做可行的原因是分子都是正的，这样以后就化除为乘，避免了精度误差。

code

il int y(int i) { return f[i] + sum[i] * sum[i]; }
il int x(int i) { return sum[i]; }//用函数表示y 和 x 更为直观

il int dy(int i,int j) { return y(i) - y(j); }//delta y 
il int dx(int i,int j) { return x(i) - x(j); }//delta x

signed main()
{
	for(re int i=1;i<=n;i++) c[i] = read() , sum[i] = sum[i-1] + c[i];//预处理
	head = 1 , tail = 0;
	for(re int i=1;i<=n;i++)
	{
		while(head < tail && dy(i-1,q[tail]) * dx(q[tail],q[tail-1]) <= dy(q[tail],q[tail-1]) * dx(i-1,q[tail])) tail--;//维护队尾，化除为乘
		q[++tail] = i-1;//入队
		while(head < tail && dy(q[head+1],q[head]) <= dx(q[head+1],q[head]) * 2 * sum[i]) head++;//排除过时点
		int j = q[head];
		f[i] = f[j] + (sum[i]-sum[j]) * (sum[i]-sum[j]) + m;//进行转移
	}
	cout << f[n];
    return 0;
}

这样下来，每个点最多入队出队一次，时间复杂度 $\mathcal O(n)$。

P5785 [SDOI2012] 任务安排

时隔一年再做一次。

感觉这个题的重点不在斜率优化，而在于费用提前计算的思想。

朴素的 DP 是设 $f_{i,j}$ 表示前 $i$ 个机器分成 $j$ 批的最小费用。然后发现这个转移是 $\mathcal O(n^3)$ 的，因为这个 $j$ 其实上界是 $n$。你会发现第二维存在的意义就是让我知道前面分了几个批次，因为 $s$ 的存在，知道了几个批次才能知道现在的时间。然后就有了我们的费用提前计算的思想。

思考，我们新开一个批次，那么它会对这个批次及以后，一直到最后的机器产生 $s \times c_i$ 的费用，而对前面的批次没有影响。那我们就可以把这个费用从 DP 状态中提出来，给个前缀和 $sumC_i$ 和 $sumT_i$，那么从 $i+1$ 这台机器新开一个批次的贡献是 $s \times (sumC_n -sumC_i)$，那么其余的部分就不需要考虑开了几台机器了，于是我们就只需要设 $f_i$ 表示考虑到前 $i$ 个机器的最小费用，那么就有：

\[f_i = \min_{0\leq j < i}\{f_j + s \times (sumC_n-sumC_j) + sumT_i \times (sumC_i-sumC_j)\} \]

这样就是 $\mathcal O(n^2)$ 的了。

然后就是拆项斜率优化，最后变成

\[f_j - s \times sumC_j = sumT_i \times sumC_j + f_i - sumT_i \times sumC_i - s \times sumC_n \]

然后就跟上个题差不多了，但是有一个地方不同。

这个题的斜率是 $sumT_i$，你会发现这个题 $|T_i| \leq 2^8$，也就是完成一个机器的时间可以为负？？所以就不能维护一个单调队列的队头了，查询的时候用二分 $\mathcal O(\log n)$ 查询即可，总时间 $\mathcal O(n\log n)$。

il int um_nik(int l,int r,int k)
{
	if(l == r) return q[l];
	int ans = 0;
	while(l <= r)
	{
		int mid = (l+r) >> 1;
		if(dy(q[mid+1],q[mid]) <= k * dx(q[mid+1],q[mid])) l = mid + 1;
		else ans = mid , r = mid-1;
	}
	return q[ans];
}

for(re int i=1;i<=n;i++)
{
	while(head < tail && dy(i-1,q[tail]) * dx(q[tail],q[tail-1]) <= dy(q[tail],q[tail-1]) * dx(i-1,q[tail])) tail--;
	q[++tail] = i-1;
	int j = um_nik(head,tail,k(i));
	f[i] = f[j] + s * (sumc[n]-sumc[j]) + sumt[i] * (sumc[i]-sumc[j]);
}

斜率优化的习题还有

总结

在斜率优化中，我们重点讨论了多项式 $val(i,j)$ 包含 $i,j$ 的乘积项的时候，我们该怎么采取优化：把 $i$ 当作常量，$j$ 当作变量，运用单调队列维护下凸壳的方式，维护决策集合。在这之中，$x$ 是单调递增的，而对于 $k$ 是否单调，我们分成了两种解法：

若 $k$ 单调，就可以维护队头，把过时点删去；
若 $k$ 不单调，说明队头是不能删掉的，我们仅在队尾维护凸壳，查询的时候 $\mathcal O(\log n)$ 查询即可。

若 $x$ 不是单调递增的，又有两种方法

若 $k$ 是单调递增的，那么我们可以倒序 DP，设计出一个方程，让 $k$ 在这个方程里变成 $x$，$x$ 在这个方程里变成 $k$，于是就转化成了上面的第二种情况，单调队列+二分维护即可。
若 $k$ 也不是单调的，这就意味着我们要在凸壳的任意位置动态插入顶点，动态查询。这时候就要用平衡树来维护凸壳了，这超出了我们的讨论范围，也超出了我的能力范围/cy。

总之，斜率优化的板子较为固定，运用一个函数来表示 $x,y$ 的话，几乎每个题中变动的就只有这个函数里的取值，所以还是比较容易练的。

决策单调性-分治（1D/2D)

四边形不等式

这东西太扯了。

首先给出定义，设 $w(x,y)$ 是定义在整数集合上的二元函数，对于定义域上的任意整数 $a\leq b \leq c \leq d$，都有

\[w(a,d) + w(b,c) \ge w(a,c) + w(b,d) \]

成立，则称 $w$ 满足四边形不等式，简单来说，就是包含和 $\ge$ 交叉和，他还有另一种形式，对于 $i<j$，都有

\[w(i,j+1) + w(i+1,j) \ge w(i,j) + w(i+1,j+1) \]

这两种可以互相推出，也是挺好推的。

在区间类（2D1D）动态规划中的应用

在区间类动态规划中，我们会遇到这样的柿子：

\[f(l,r) = \min_{l\leq k \leq j-1}\{f(l,k)+f(k+1,r)\} + w(l,r) \]

注意，只能是 $\min$，因为这个式子是 2D1D，所以复杂度是 $O(n^3)$ 的，若 $w(l,r)$ 满足两个性质，我们就可以利用决策单调性来优化：

区间包含单调性：包含包含，就是让你证明 $w(i,j+1) \ge w(i+1,j)$ 恒成立。
四边形不等式：若对于任意 $a\leq b \leq c \leq d$，都有 $w(a,d) + w(b,c) \ge w(a,c) + w(b,d)$，则称 $w$ 满足四边形不等式，当然从另一个形式推也是可以的。

然后有一个引理：

若 $w(l,r)$ 满足区间包含单调性和四边形不等式，则状态 $f(l,r)$ 满足四边形不等式。

证明我都略了，感兴趣的可以到 OI-Wiki 上看。

然后又有一个定理，我们设 $p(l,r)$ 表示 $[l,r]$ 区间内的最优决策点，那么有：

若状态 $f$ 满足四边形不等式，则有 $p(l,r-1) \leq p(l,r) \leq p(l+1,r)$。

也就是说最优决策点具有一定单调性。我们可以发现类似于区间 DP 中，当我们找 $(l,r)$ 的最优决策点时，显然 $(l,r-1),(l+1,r)$ 的最优决策点我们已经找好了，那我们于是就可以缩小枚举范围，只枚举这两个点之间的点即可，然后可以证明，这样的复杂度就由 $O(n^3)$ 缩减到了 $O(n^2)$。

上面这一串说明什么，说明我们只要证明了 $w$ 的性质，我们便可以减少枚举量，降低复杂度。但是有可能 $w$ 的性质很难证明，怎么办？打表，如果打了很多次都满足这两个条件，那么说明这个 $w$ 很有可能满足这个性质，我们就可以用决策单调性来优化了。

在 1D1D 动态规划中的应用

四边形不等式的性质还适用于以下这种 1D1D 的方程：

\[f(r) = \min_{l=1}^{r-1}\{f(l) + w(l,r)\} \]

其中有一个定理：

若 $w(l,r)$ 满足四边形不等式，则对于任意 $r_1 \leq r_2$，都有 $p_{r_1}\leq p_{r_2}$

这种对于上界不确定的决策单调性，我们一般采用分治算法来进行求解。设 $f(tl,tr,l,r)$ 表示我们要求解 $f(l) \sim f(r)$ 的答案，并且决策集合是 $[tl,tr]$，我们每次暴力找 $\text{mid}$ 的最优决策点，然后分治成两部分，$f(tl,mid,l,mid-1)$ 和 $f(mid,tr,mid+1,r)$，可以证明，这样分治下去，时间复杂度是 $O(n\log n)$。

算法流程

这个其实和上面 1D1D 的类似。一般用来解决 2D1D 的 DP 问题。它适用的情况是只有上一层向下一层转移，同层之间不能转移，就类似于 01 背包，而不是完全背包。

一般的状态转移方程是这样的：

\[f(i,j) = \min_{k<j}\{f(k,j-1) + w(k+1,i)\} \]

也有可能是 $w(k,i)$，或者说 $i,j$ 顺序是反过来的，不过本质是一样的，我们只需要找到那个上层转移到下层的一维，并对另一维进行分治即可。

思路是类似的，对于每一层，设当前层是 $j$，那么 $f(tl,tr,l,r)$ 表示我们要求解 $f(l,j) \sim f(r,j)$ 的答案，并且决策集合是 $[tl,tr]$，我们每次暴力找 $\text{mid}$ 的最优决策点（这个我们可以用另一个数组 $g$ 存上一层的状态，然后进行转移），然后分治成两部分，$f(tl,mid,l,mid-1)$ 和 $f(mid,tr,mid+1,r)$，可以证明，这样分治下去，时间复杂度是 $O(n\log n)$，并且因为我们一定要转移 $k$ 层，所以是总复杂度就是 $O(nk\log n)$，空间复杂度 $O(n)$。大致代码长这样(以 $\max$ 为例，$\min$ 可以自己替换一下)：

il void Divide(int tl,int tr,int l,int r)
{
	int mid = (l+r) >> 1;
	int Max = -1 , pos = -1;
	for(re int i=tl;i<=min(mid-1,tr);i++)
	{
		if(g[i] + w(i+1,mid) > Max)
			Max = g[i] + w(i+1,mid) , pos = i;
	}
	f[mid] = max(f[mid],Max);
	if(l < mid) Divide(tl,pos,l,mid-1);
	if(r > mid) Divide(pos,tr,mid+1,r);
}

技巧：贡献难算

如果 $w$ 不能在 $O(1)$ 的时间内计算出来或者说预处理的时间复杂度过高难以接受，但是如果 $l \sim r$ 的贡献能够在 $O(v)$ 的时间内拓展到 $(l\pm 1)\sim (r\pm 1)$，那么决策单调性分治依然可以在 $O(nv\log n)$ 的复杂度内求出每一层的状态。可以类比莫队的移动方式，维护当前贡献区间的左右端点 $l,r$，如果要查询某个区间的贡献，直接左右端点跳到该区间。

以 CF833B The Bakery 为例，这个题转移方程也是很好求的，然后决策单调性也可以感性理解，就是分的段越长越有可能不优。但是这个题的 $w$ 是求 $[l,r]$ 内不同数的个数，不是很好求，但是我们可以用类似莫队的方式来 $O(1)$ 移动，那么每转移一层的复杂度就还是 $O(n\log n)$，总共转移 $k$ 层，那么就是 $O(nk\log n)$。

决策单调性-二分队列(1D)

二分队列常用来优化具有决策单调性的 DP 问题，且这里的决策单调性指的是对于 $i$ 和 $j$ 的最优决策点 $p_i,p_j$，若 $i < j$，那么 $p_i\leq p_j$ 一定成立。要求转移时的贡献能够快速计算，一般是 $O(1)$

通常情况的限制是：贡献函数二阶导恒为非负，求最小值 或 二阶导恒为非正，求最大值。用人话说，就是对于一个 凹函数，求最小值 或 凸函数，求最大值。比如 $y=x^2$ 这个函数就是凹函数，而 $y=-x^2$ 这个函数就是凸函数，可以对照图像自己理解“凹凸”的意义。

具体地，建立一个存储三元组 $(pos,l,r)$ 的队列，表示 $l\sim r $ 的最优决策点是 $pos$。每次判断队首三元组是否过时，也就是是否 $r < i$，如果是，弹出队首；否则将 $l$ 赋值为 $i$。

加入决策时，如果 $i$ 相比队尾的 $j = q[tail].pos$ 转移到 $q[tail].l$ 更优秀，那么根据决策单调性，我们可知 $i$ 转移到 $q[tail].l \sim n$ 比 $j$ 更优，因此
$(pos,l,r)$ 就完全没用了，弹出。重复这个操作直到不满足条件或者队列只剩下一个三元组。

接下来我们取出队尾的三元组 $(pos,l,r)$，我们要找到一个位置 $p$，使得 $p$ 以前的位置，从 $pos$ 转移更优；而 $p$ 及 $p$ 以后的位置，从 $i$ 转移更优。因为这个贡献是可以快速计算出来的，而又满足决策单调性，所以我们可以二分出来，注意二分的位置是 $l$ 到 $r+1$，如果 $p\leq n$，那么我们将 $(i,p,n)$ 压入队列，然后把原队尾三元组的 $r$ 改为 $p-1$。

可以看出，整个算法的复杂度是 $O(n\log n)$ 的。

例题：P1912 [NOI2009] 诗人小G

#include<bits/stdc++.h>
#define double long double
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e5 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

int T,n,L,P;
int head,tail;
int sum[N],cha[N],stk[N];
double f[N];
char ch[N][35];
struct node{
	int pos,l,r;
}q[N];

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

il double ksm(double a,int b)
{
	double res = 1;
	while(b)
	{
		if(b&1) res = res * a;
		a = a * a;
		b >>= 1;
	}
	return res;
}

il double Calc(int i,int j) { return f[j] + ksm(fabs(sum[i]-sum[j]-L),P); }

il int um_nik(int x,int y,int l,int r)
{
	int ans = 0;
	while(l < r)
	{
		int mid = (l+r) >> 1;
		if(Calc(mid,x) >= Calc(mid,y)) r = mid;
		else ans = mid + 1 , l = mid + 1;
	}
	return ans;
}

il void Main()
{
	n = read() , L = read() + 1 , P = read();
	for(re int i=1;i<=n;i++)
	{
		cin >> ch[i];
		sum[i] = sum[i-1] + strlen(ch[i]);
	}
	for(re int i=1;i<=n;i++) sum[i] += i;
	q[1] = {0,1,n} , head = 1 , tail = 1;
	for(re int i=1;i<=n;i++)
	{
		while(head < tail && q[head].r < i) head++;//判断是否过时
		q[head].l = i;
		f[i] = Calc(i,q[head].pos) , stk[i] = q[head].pos;
		while(head < tail && Calc(q[tail].l,i) <= Calc(q[tail].l,q[tail].pos)) tail--;//判断谁转移到l更优
		int pos = um_nik(q[tail].pos,i,q[tail].l,q[tail].r+1);//找到位置 p
		if(pos <= n) q[tail].r = pos-1 , q[++tail] = {i,pos,n};//压入队列
	}
	if(f[n] > 1e18) puts("Too hard to arrange");
	else
	{
		printf("%.0Lf\n",f[n]);
		int i;
		for(q[tail=0].pos=i=n;i;q[++tail].pos=i=stk[i]);
		for(;tail;--tail)
		{
			for(i=q[tail].pos+1;i<q[tail-1].pos;++i)
				printf("%s ",ch[i]);
			puts(ch[i]);
		}
	}
	puts("--------------------");
}

signed main()
{
	T = read();
	while(T--) Main();
	return 0;
}

决策单调性-二分栈(1D)

二分栈常用来优化具有以下决策单调性的 DP 问题中：每个决策点 $j$ 只会被它更前的决策点 $i(i<j)$ 反超。记 $w(i)$ 为从决策点 $i$ 转移到当前位置的贡献。

但其实这个不是严格的决策单调性，但只要满足这个条件即可。

通常情况的限制是：贡献函数二阶导恒为非负，求最大值 或 二阶导恒为非正，求最小值。用人话说，就是对于一个 凹函数，求最大值 或 凸函数，求最小值，这个可以和二分队列对比一下。

我们用一个栈维护可能的决策点，那么栈顶储存的就是当前位置的决策点。我们考虑如何更新它：一个很朴素的想法是如果栈顶劣于次栈顶就弹出。但这样其实是不完善的，举个反例：如果存在 $i<j<k$ 满足 $k$ 优于 $j$ 但劣于 $i$，那么这个算法会从 $k$ 转移而不是正确的从 $i$ 转移过来。但是我们有补救的机会：如果 $i$ 反超 $j$ 的时间在 $j$ 反超 $k$ 的时间之前，那么说明在 $i$ 反超 $j$ 的时候，$j$ 还没反超 $k$，这就说明 $j$ 永远不会成为最优决策，此时我们就可以弹出 $j$ 了。因此，我们可以在加入决策 $k$ 之前二分出 $j$ 反超 $k$ 的时间 $t_1$ 和 $i$ 反超 $j$ 的时间 $t_2$，如果 $t_1 \ge t_2$，那么弹出 $j$。重复上述操作直到栈内只剩一个元素或 $t_1 < t_2$，然后压入 $k$。

这样操作完了以后，不要忘记每次转移前要执行我们那个朴素的想法，即二分出次栈顶反超栈顶的时间 $t$，如果不大于当前时间 $i$，那么弹出栈顶。

因为有次栈顶这个东西存在，所以我们可以用 vector 来代替 stack。

例题：P5504 [JSOI2011] 柠檬

非常好题目，爱来自瓷器。

这个题的朴素 DP 很难做，因为你每次得对一个区间的 $s_0t^2$ 进行比较。但是有一个很好证明但不好想到的性质，就是 $f$ 只会在相同颜色转移。所以可以给每个颜色开个栈，维护决策集合。

因为 $s_0t^2$ 二阶导恒大于 $0$，又是求最大值，所以我们采用二分栈。

#include<bits/stdc++.h>
#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
#define tp st[c][st[c].size()-1]
#define se st[c][st[c].size()-2]
const int N = 1e5 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

int n;
int f[N],s[N],buc[N],p[N];
vector <int> st[N];

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

il int calc(int i,int cnt) { return f[i-1] + cnt * cnt * s[i]; }

il int um_nik(int x,int y)
{
	int l = p[y] , r = buc[s[y]] + 1 , ans = 0;
	while(l <= r)
	{
		int mid = (l+r) >> 1;
		if(calc(x,mid-p[x]+1) < calc(y,mid-p[y]+1)) ans = mid + 1 , l = mid + 1;
		else r = mid - 1;//找到 x 优于 y 的第一个时间点
	}
	return ans;
}

signed main()
{
	n = read();
	for(re int i=1;i<=n;i++) s[i] = read() , p[i] = ++buc[s[i]];
	for(re int i=1;i<=n;i++)
	{
		int c = s[i];
		while(st[c].size() > 1 && um_nik(se,tp) <= um_nik(tp,i)) st[c].pop_back();
		st[c].push_back(i);
		while(st[c].size() > 1 && um_nik(se,tp) <= p[i]) st[c].pop_back();
		f[i] = calc(tp,p[i]-p[tp]+1);
	}
	cout << f[n];
	return 0;
}

posted @ 2023-07-10 15:04 Bloodstalk 阅读(32) 评论(2) 编辑收藏举报

刷新页面返回顶部

bloodstalk

动态规划（Ⅲ）

前言

倍增优化 DP

例题

倍增优化 DP

求解问题

解决根源的初始化

总结

数据结构优化 DP

例题

总结

单调队列优化 DP(\(t\)D/\(e\)D)

适用情况

例题

单调队列优化多重背包

总结

斜率优化(1D)

例题

总结

决策单调性-分治（1D/2D)

四边形不等式

在区间类（2D1D）动态规划中的应用

在 1D1D 动态规划中的应用

算法流程

技巧：贡献难算

决策单调性-二分队列(1D)

决策单调性-二分栈(1D)

公告