高中数学瞎记

数列

表示

常用 \(\{a_n\}\) 表示一个长度为 \(n\) 的数列。

分类

按项数分，可以分为有穷数列和无穷数列。

按单调性分，可以分成

• 递增序列：\(\forall n \in \mathbb{N}^+,a_{n+1} \ge a_n\)。

  若是严格递增，则是 \(a_{n+1} > a_n\)。

• 递减序列：\(\forall n \in \mathbb{N}^+,a_{n+1} \leq a_n\)。

  若是严格递减，则是 \(a_{n+1} < a_n\)。

• 摆动数列：没有单调性。

• 常数列：每项都一样的数列。

公式

有些数列有着通项公式：

\(\{1,3,5,7,\dots\}\)，这个数列的通项公式就是 \(\forall n\in \mathbb{N}^+,a_n = 2n-1\)

有些数列有着递推公式：

\(\{1,1,2,3,5,\dots\}\),即斐波那契数列，它的递推公式就是 \(\forall n\in \mathbb{N}^+,n>2, a_n = a_{n-1}+a_{n-2}\)

有些数列啥都没有，没有好的性质，所以不考。

等差数列

类似于 \(\{1,3,5,7,\dots\}\) 这样的数列，它们每两项的差是一个相等的数，我们就说这个数列是等差数列。

首项和公差

在上面这个例子中，\(a_1=1\) 即为它的首项，\(d=3-1=2\) 即为它的公差。

有了这两个概念后，数列的每一项，以及数列一段的和都能被表示出来了。

公式

第 \(n\) 项：\(a_n = a_1 +(n-1)d\)。

等差数列前 \(n\) 项和：\(S_n = na_1 + \frac{n(n-1)}{2}d = \frac{(a_1+a_n)n}{2}\)。

中项公式：若 \(a,b,c\) 是等差数列相邻的 \(3\) 项，则有 \(2b = a+c\)。

四项公式：若 \(p,q,m,n\in \mathbb{N^+},p+q = m+n\) ，那么在一个等差数列中有 \(a_p+a_q = a_m+a_n\)

等比数列

类似于 \(\{2,4,8,16,\dots\}\) 这样的数列，它们每两项的比值是一个相等的数，我们就说这个数列是等比数列。

首项和公比

在上面这个例子中，\(a_1=2\) 即为它的首项，\(q=4\div 2=2\) 即为它的公比，其中，公比不为 \(0\)。当 \(q=1\) 的时候，这就成为了一个常数列。

公式

第 \(n\) 项：\(a_n = a_1 \times q^{n-1}\)。

等比数列前 \(n\) 项和：

\[s_n = \left\{ \begin{aligned} & na_1 ,\ \ \ \ \ q=1 \\ & \frac{a_1(1-q^n)}{1-q},q\not=1\text{且}q\not=0 \end{aligned} \right. \]

错位相减，正序相加。

中项公式：若 \(a,b,c\) 是等比数列相邻的 \(3\) 项，则有 \(b^2 = ac\)。

四项公式：若 \(u,v,m,n\in \mathbb{N^+},u+v = m+n\) ，那么在一个等比数列中有 \(a_ua_v=a_ma_n\)

做题套路

累加法

\[\left\{ \begin{aligned} & a_n-a_{n-1}=\dots \\ & a_{n-1}-a_{n-2}=\dots \\ \vdots \\ & a_2-a_1 =\dots \end{aligned} \right. \]

相加求和得到 \(a_n-a_1 = \dots\) ，进而得到通项公式。

进阶：

\(a_{n+1} = 3a_n + 2\cdot 3^n + 1\)

这种题要保证 \(a_n\) 前的系数和幂的底数相等。

同除 \(3^{n+1}\)，得

\[\frac{a_{n+1}}{3^{n+1}} = \frac{a_n}{3^n} + \frac{2}{3}+\frac{1}{3^{n+1}} \]

设 \(\large b_n = \frac{a_n}{3^n}\)

则有

\[b_{n+1} = b_n +\frac{2}{3}+\frac{1}{3^{n+1}} \]

\[\left\{ \begin{aligned} & b_n-b_{n-1}=\frac{2}{3}+\frac{1}{3^n} \\ & b_{n-1}-b_{n-2}=\frac{2}{3}+\frac{1}{3^{n-1}} \\ \vdots \\ & b_2-b_1 =\frac{2}{3} + \frac{1}{9} = \frac{7}{9} \end{aligned} \right. \]

相加即可，别忘了最后是求 \(a_n\)。

累乘法

\[\left\{ \begin{aligned} & a_n=q_na_{n-1} \\ & a_{n-1}=q_{n-1}a_{n-2} \\ \vdots \\ & a_2=q_1a_1 \end{aligned} \right. \]

左右分别相乘，再消去，这个 \(q\) 需要有一个通项公式才能做。

进阶：

\(a_{n} = 2n\cdot5^{n-1}a_{n-1}\)

则有

\[\left\{ \begin{aligned} & a_n=2n\cdot5^{n-1}a_{n-1} \\ & a_{n-1}=2(n-1)\cdot5^{n-2}a_{n-2} \\ \vdots \\ & a_2=2\cdot 2\cdot 5 \cdot a_1 \end{aligned} \right. \]

观察右边式子，相乘，得到

\[2^{n-1}n!5^{1+2+\dots +n-1}(a_1a_2\dots a_n) \]

左右相消

\[a_n = 2^{n-1}n!5^{\frac{n(n-1)}{2}}a_1 \]

有些题要注意下标。

待定系数法

\(a_{n+1} = 3a_n + 4\)

这种题考虑把这个 \(4\) 整没了，怎么整没？

设

\[a_{n+1} +\alpha = 3(a_n + \alpha) \]

设 \(b_n= a_n + \alpha\)，就有 \(b_{n+1} = 3b_n\)，转化成等比数列。

求 \(\alpha\) 也很简单，移项一下，得到 \(3\alpha - \alpha = 4,\alpha = 2\)。

\(a_{n+1} = 3a_n + 4n\)

照样来

\(a_{n+1} + \alpha(n+1) + \beta = 3(a_n + \alpha n + \beta)\)

加 \(\beta\) 的目的是让它平衡。

\[\left\{ \begin{aligned} & 2\alpha = 4 \\ & 2\beta -\alpha = 0 \\ \end{aligned} \right. \]

解出来换元即可。

换元法

\(a_{n+1} = \frac{1}{16}(1+4a_n + \sqrt{1+24a_n})\)

设 \(b_n = \sqrt{1+24a_n}\)

则有 \(a_n = \frac{b_n^2 - 1}{24}\)

原式就变成了：

\[\frac{b_{n+1}^2-1}{24} = \frac{1}{16}(1+\frac{b_n^2-1}{6}+b_n) \]

\[4(b_{n+1}^2-1) = b_n^2 + 6b_n + 5 \]

\[4b_{n+1}^2 = b_n^2 + 6b_n + 9 = (b_n+3)^2 \]

因为 \(b_n \ge 0\)，所以

\[2b_n+1 = b_n + 3 \]

\[b_{n+1} = \frac{1}{2}b_n + \frac{2}{3} \]

待定系数法求解即可。

等差等比数列的和与通项公式的特殊关系

等差数列

\[\left\{ \begin{aligned} & a_n = a_1 + (n-1)d \\ & s_n = na_1 + \frac{n(n-1)}{2}d \\ \end{aligned} \right. \]

\[\frac{s_n}{n} = a_1 + (n-1)\frac{d}{2} \]

是一个首项为 \(a_1\)，公差为 \(\frac{d}{2}\) 的等差数列。

对于一个等差数列 \(\{a_n\}\)，每 \(m\) 个分一组，组内数相加，构成一个新的数列 \(\{b_n\}\)，那么新数列仍是等差数列，它的首项为 \(a_1+a_2+\dots+a_m\)，公差为 \(m^2d\)。

两个等差数列 \(\{a_n\},\{b_n\}\) 和分别是 \(S_n,T_n\)，则有

\[\frac{S_{2n-1}}{T_{2n-1}} = \frac{a_n}{b_n} \]

等比数列

1. 对于一个等比数列 \(\{a_n\}\)，每 \(m\) 个分一组，组内数相加，构成一个新的数列 \(\{b_n\}\)，那么新数列仍是等比数列，它的首项为 \(a_1+a_2+\dots+a_m\)，公比为 \(q^m\)。

\(a_n\) 和 \(s_n\) 的关系

\(a_n = s_n - s_{n-1} , n\ge 2\)

错位相减

当一个等差数列 \(\{a_n\}\) 和等比数列 \(\{b_n\}\) 相乘构成一个新的数列 \(\{a_nb_n\}\) 时，就可以运用错位相减法。

已知 \(S_n = 2a_n-2n-1\) ，并证得 \(\{a_n+2\}\) 是等比数列，求数列 \(\{n\cdot (a_n+2)\}\) 的前 \(n\) 项和

\[S_n = 1\cdot5\cdot2^0 + 2\cdot5\cdot2^1 + \dots + n\cdot5\cdot2^{n-1} \]

\[2S_n = 1\cdot5\cdot2^1 + 2\cdot5\cdot2^2 + \dots + n\cdot5 \cdot2^n \]

\[2S_n - S_n = -5 -5(2^1+2^2+\dots+2^{n-1}) + n\cdot5\cdot2^n \]

把 \(-5\) 放进去

\[= -5(2^0+2^1+\dots +2^{n-1}) + n\cdot5\cdot2^n \]

\[=5n\cdot2^n-5(2^n-1)=5\cdot2^n(n-1)+5 \]

更普适的：

\[a_n = a_1 + (n-1)d , b_n = b_1q^{n-1} \]

\[S_n = a_1b_1 + a_2b_2 + \dots + a_nb_n \]

\[=a_1b_1+(a_1+d)b_1q+(a_1+2d)b_1q^2 + \dots + [a_1+(n-1)d]b_1q^{n-1} \]

\[qs_n = a_1b_1q+(a_1+d)b_1q^2+(a_1+2d)b_1q^3 + \dots + [a_1+(n-1)d]b_1q^{n} \]

\[(q-1)S_n = a_nb_n-db_1(q+q^2+\dots+q^{n-1})-a_1b_1 \]

\[S_n = \frac{a_nb_n-db_1(q+q^2+\dots+q^{n-1})-a_1b_1}{q-1} \]

裂项相消

要求解 \(\frac{1}{1\times 2} + \frac{1}{2\times 3}+\dots+\frac{1}{n(n+1)}\)

运用一个裂项的方法:\(\frac{1}{n\times (n+1)} = \frac{1}{n}-\frac{1}{n+1}\)

于是式子就变成了

\[(\frac{1}{1}-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+\dots+(\frac{1}{n}-\frac{1}{n+1}) \]

\[= 1-\frac{1}{n+1} = \frac{n}{n+1} \]

这就是裂项相消的思想。

\[\frac{1}{n(n+k)} = \frac{1}{k}(\frac{1}{n}-\frac{1}{n+k}) \]

本质通分，差多少补多少。

\(\large \frac{1}{\sqrt{n+1}+\sqrt n} = \frac{\sqrt{n+1}-\sqrt n}{(\sqrt{n+1}+\sqrt n)(\sqrt{n+1}-\sqrt n)} = \sqrt{n+1}-\sqrt n\)

也是一种裂项，本质是分母有理化。

\(\large \frac{1}{n(n+1)(n+2)} = \frac{1}{2}(\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)})\)

倒序相加和分组求和

求 $ \sin²¹ + \sin²²+\dots+\sin²⁸⁹$

\[\text{令}S= \sin^21^{\circ} + \sin^22^{\circ}+\dots+\sin^289^{\circ} \]

\[S= \sin^289^{\circ} +\dots+\sin^22^{\circ}+\sin^21^{\circ} \]

\[2S= (\sin^21^{\circ}+\cos^21^{\circ}) + (\sin^22^{\circ}+\cos^22^{\circ})+(\sin^289^{\circ}+\cos^289^{\circ}) =89 \]

\[S = \frac{89}{2} \]

求 \(\large (x+\frac{1}{x})^2+(x^2+\frac{1}{x^2})^2+\dots+(x^n+\frac{1}{x^{n}})^2\)

展开得

\[(x^{2\cdot1}+\frac{1}{x^{2\cdot1}}+2)+(x^{2\cdot2}+\frac{1}{x^{2\cdot2}}+2)+\cdots+(x^{2\cdot n}+\frac{1}{x^{2\cdot n}}+2) \]

\[=(x^2+x^4+\dots+x^{2n})+(\frac{1}{x^2}+\frac{1}{x^4}+\dots+\frac{1}{x^{2n}})+2n \]

\[=\frac{x^2(1-x^{2n})}{1-x^2}+\frac{\frac{1}{x^2}(1-\frac{1}{x^{2n}})}{1-\frac{1}{x^2}} + 2n \]

\[= \frac{x^2(x^{2n}-1)}{x^2-1}+\frac{1-\frac{1}{x^{2n}}}{x^2-1} + 2n \]

\[= \frac{x^{2n+2}-x^2+1-\frac{1}{x^{2n}}}{x^2-1}+2n \]

\[=\frac{x^{4n+2}-x^{2n+2}+x^{2n}-1}{x^{2n}(x^2-1)}+2n \]

\[=\frac{(x^{2n}-1)(x^{2n+2}+1)}{(x^2-1)x^{2n}} + 2n \]

所以

\[ans = \left\{ \begin{aligned} & \frac{(x^{2n}-1)(x^{2n+2}+1)}{(x^2-1)x^{2n}} + 2n,x\not=\pm1 \\ & 4n\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=\pm1 \\ \end{aligned} \right. \]

导数

见导数、积分瞎记。

组合数学

见组合数学

以下是 OI 中可能用不上的。

\[C_n^k = \frac{n(n-1)\dots(n-k+2)(n-k+1)}{k(k-1)!} \]

\[=C_n^{k-1}\cdot\frac{n-k+1}{k} \]

因此我们有

\[\left\{ \begin{aligned} & C_n^k > C_n^{k-1},0<k<\frac{n+1}{2} \\ & C_n^k < C_n^{k-1},k>\frac{n+1}{2} \\ & C_n^k = C_n^{k-1},k=\frac{n+1}{2}\text{且} n \text{为奇数} \end{aligned} \right. \]

这个看杨辉三角也能发现这个规律，并且通过这个可以看出，\(C_n^k\) 的值先增大再减小，最大值的情况为

\[\left\{ \begin{aligned} & (C_n^k)_{\max} = C_n^{\frac{n+1}{2}} = C_n^{\frac{n-1}{2}},n\text{为奇数} \\ & (C_n^k)_{\max} = C_n^{\frac{n}{2}},n\text{为偶数} \end{aligned} \right. \]

捆绑法与插空法

插空法

甲乙丙丁戊己 \(6\) 人排队，要求甲乙丙三位同学两两不相邻。

解：先把丁戊己三个人放到队列里头，这样有 \(A_3^3\) 种情况。

丁戊己三个人之前形成了 \(4\) 个空位置，假设排的是丁戊己，具体就是

空\(1\) | 丁 | 空\(2\) | 戊 | 空\(3\) | 己 | 空\(4\)

让甲乙丙 \(3\) 个人插到这 \(4\) 个空里就行，就是 \(A_4^3\)。

分步乘法，最后答案就是 \(A_3^3 \times A_4^3\)。

捆绑法

还是这个题，换一个条件：甲、乙两同学不相邻，且乙、丙两同学也不相邻。

解：这个题显然可以分类讨论一下：甲丙不相邻、或者相邻。

• 第一种情况其实就是甲乙丙互不相邻，答案就是前面的 \(A_3^3 \times A_4^3\)。

• 第二种情况就是甲丙相邻，这时候考虑捆绑法，也就是把甲丙当成一个去考虑。

  • 因为捆绑的时候顺序不确定，所以首先有一个 \(A_2^2\)，也就是说甲丙或丙甲都行

  • 甲丙捆绑后和乙不相邻，考虑插空法，还是把另外三个人排一下，这样就是 \(A_3^3\)。

  • 然后让甲丙和乙放进这 \(4\) 个空中的两个去，答案就是 \(A_4^2\)。

  • 所以这种情况的答案就是 \(A_2^2\times A_3^3 \times A_4^2\)。

• 最后的答案就是 \(A_3^3\times A_4^3 + A_2^2\times A_3^3 \times A_4^2 = 144+144=288\)

---

还是这个题，再换条件：要求甲乙相邻，丙丁相邻，求方案数。

解：这个还是比较容易的。把甲乙捆一块，丙丁捆一块，由于它们内部有顺序，所以会产生 \(A_2^2 \times A_2^2\) 的贡献。捆绑完了以后，就还剩下 \(4\) 部分，它们没有限制，那么就是 \(A_4^4\)。所以答案就是 \(A_2^2\times A_2^2 \times A_4^4 = 96\)。

隔板法

把 \(10\) 个球分到 \(7\) 个班里，每个班至少要分到一个球，问有几种不同的分法。

隔板法，顾名思义，就是模拟了一个放板子的过程。例如我在两个球之间放了一个板子，那么这个板子的意义就是把这两个球给到不同的班。

理解了这个意思后，这个题也就比较简单了：\(10\) 个球之间有 \(9\) 个空，我们只需要把 \(6\) 个板子放进去，就能分到 \(7\) 个班里，并且每个班至少能分到 \(1\) 个球。最后的答案就是 \(C_9^6=84\)。

---

这个就比较巧妙了。

求 \(x_1+x_2+x_3+x_4 = 10\) 的正整数解。

乍一看，可能没有什么头绪，但是细想，把 \(10\) 分成 \(10\) 个 \(1\)，我们把这些 \(1\) 分成不同的部分，就是我们想要的正整数解。

于是这个问题就转换成了插板法，在 \(9\) 个空中插 \(3\) 个板子，答案就是 \(C_9^3 = 84\)。

---

如果是求非负整数解，如何考虑？

也是一个 trick：我们将每个数都加上 \(1\)，即

\[(x_1+1)+(x_2+1)+(x_3+1)+(x_4+1) = 14 \]

令 \(y_i = x_i + 1\)，这题就变成了普通的插板法。

由于 \(x_i\) 和 \(y_i\) 构成的是双射，即一一对应，所以 \(y_i\) 的正整数解就对应着 \(x_i\) 的非负整数解。

最后答案就是 \(C_{13}^3 = 286\)。

---

\(12\) 个小球放入编号为 \(1,2,3,4\) 的盒子中，要求每个盒子中的小球个数不小于其编号数，问不同的方法有多少种。

一种最直接的处理方式：先保底，把每个盒子至少需要的球先放进去，因为这么做以后这个题就变成了 \(x_1+x_2+x_3+x_4=2\) 的非负整数解，按照上面的 trick 做就行了。

分组分配问题

平均分配

把 \(abcd\) 平均分成两组，问有多少种分法。

枚举一下，我们得到 \(ab/cd,ac/bd,ad/bc\) 这三种情况。

考虑组合意义，就是先从 \(4\) 个中选两个，再从 \(2\) 个中选 \(2\) 个，就是 \(C_4^2\times C_2^2 = 6\)。

我们发现，答案是不对的，为什么呢？因为我们在 \(C_4^2\) 的时候，假设我们选的是 \(bd\)，那么剩下的就是 \(ac\)；如果我们选的 \(ac\)，剩下的就是 \(bd\)，这两种本质上是一样的，但是我们给它记上了，所以我们要除以一个 \(A_2^2\) 来消除这种枚举顺序的影响。分成 \(x\) 组，就除以 \(A_x^x\) 。

其实最后这个式子是一个 \((2n+1)!!\) ，即

\[\sum_{2i<n}(2i+1) \]

这个题要注意与将 \(abcd\) 分给甲乙两个人的情况的区别，甲乙两个人是不同的，所以是一种排列，而不是平均分成两组这样没有顺序的，所以这种情况不需要除以 \(A_2^2\)。

不均分配

\(6\) 本不同的书。

\(Q_1:\) 分给甲乙丙三个人，甲 \(1\) 本，乙 \(2\) 本，丙 \(3\) 本。

\(A_1\)：这个比较简单，直接 \(C_6^1\times C_5^2 \times C_3^3 = 60\) 即可，因为甲乙丙三人本质不同。

\(Q_2\)：一份 \(1\) 本，一份 \(2\) 本，一份 \(3\) 本。

\(A_2\)：其实这个题也是 \(C_6^1\times C_5^2 \times C_3^3 = 60\)。为什么不用除以 \(A_3^3\) 了呢？因为这是不平均分配，组与组之间是不同的，存在着一种顺序，所以不用。

\(Q_3\)：分给甲乙丙 \(3\) 人，一人 \(1\) 本，一人 \(2\) 本，一人 \(3\) 本。

\(A_3\)：这个要在 \(C_6^1\times C_5^2 \times C_3^3 = 60\) 的基础上 \(\times A_3^3\) ，意思就是把不同数量的书给不同的人，就是将这三堆分给甲乙丙，做一个全排列。

部分平均分配

\(Q_1\)：将 \(6\) 本书分给甲乙丙 \(3\) 人，甲得 \(4\) 本，乙丙各得 \(1\) 本

\(A_1\)：答案即 \(C_6^4 \times C_2^1 \times C_1^1 =30\)，因为三个人的本质不同，存在差异。

\(Q_2\)：一份 \(4\) 本，其余两份都是 \(1\) 本

\(A_2\)：答案是 \(C_6^4 \times \frac{C_2^1\times C_1^1}{A_2^2} = 15\)，也就是说后面两个是没有顺序的，要消除顺序的影响。

总结

其实就是没有顺序，相同的部分要排除顺序的影响，即除以组数的全排列。

染色问题

这个问题比较妙，建议直接看一数。

总结就是先分类，再跳格。跳格的时候有不想相邻的跳到不相邻的，没有不相邻的就随便跳到一个相邻的。

正难则反

我的个签/cy。

从 \(8\) 男 \(4\) 女中选 \(5\) 名同学，至少有一名女同学，问有多少种情况。

至少 \(1\) 名女同学包含了很多种不同的情况，要分类讨论，不大行。

正难则反，考虑它的互斥事件，也就是一个女生都没有，那么就是 \(C_8^5\)，什么限制也没有的情况是 \(C_{12}^5\)，那么至少有一名女生的情况就是 \(C_{12}^5-C_8^5\)。

---

地面上有并排的 \(7\) 个车位，有颜色为 \(A,B,C,D\) 的 \(4\) 辆不同汽车放进去，放完后，恰有两个连续的空车位，且A、B两车互不相邻的情况有多少种？

解：这个两车互不相邻比较恶心，直接正难则反，把它俩捆一块用捆绑法来做就非常可以。

• 先不管它相邻不相邻，算总方法：这又有一个正难则反，你可以把车放进去，让空车位插进它们的空位之间，运用插空法来做，这部分的答案就是 \(A_4^4\times A_5^2\)，因为你把两个连续的空车位也捆绑打包了所以车位本质是不同的。
• 再考虑两车相邻的情况：首先是车内部的排序，\(A_2^2\times A_3^3\)，因为 \(AB\) 打包了，所以是 \(4\) 个空位，最后答案就是 \(A_2^2 \times A_3^3 \times A_4^2\)。
• 那么不相邻的情况就是 \(A_4^4\times A_5^2 - A_2^2 \times A_3^3 \times A_4^2=336\) 了。

概率与统计

概率

这一部分在概率论里。

统计

一元线性回归模型

相关关系

相关关系：两个变量之间的关系，统计学上都统称为相关关系。两个变量之间的关系有可能具有确定性，比如圆的面积 \(s\) 与半径 \(r\) 的关系、固定面积的长方形长 \(x\) 和宽 \(y\) 之间的关系；也有可能有一定的关系，但是并没有确定性，带有一定的随机性，比如人的身高 \(h\) 和体重 \(w\) 的关系。

散点图：把收集到的变量 \(x\) 和变量 \(y\) 的 \(n\) 对数据（简称为成对数据）在平面直角坐标系 \(xOy\) 中描出点 \((x_i,y_i),i=1,2,3,\dots,n\)，就可以得到这 \(n\) 对数据的散点图。

线性相关：如果由散点图、成对数据、或是直观经验可知，变量 \(x\) 与变量 \(y\) 之间的关系可以近似地用一次函数来刻画，则称 \(x\) 与 \(y\) 线性相关。此时，如果一个变量增大，另一个变量也大体增大，则称这两个变量正相关；如果一个变量增大，另一个变量大体上减少，则称这两个变量负相关。

回归直线方程

定义

已知变量 \(x\) 和 \(y\) 的 \(n\) 对成对数据 \((x_i,y_i),i=1,2,\dots,n\)，任意给定一个一次函数 \(y=bx+a\)，对每一个已知的 \(x_i\)，由直线方程可以得到一个估计值

\[\hat{y}_i=bx_i+a \]

如果这个一次函数 \(\hat{y}=\hat{b}x+\hat{a}\) 使得

\[\sum_{i=1}^n(y_i-\hat{y}_i)^2 \]

取得最小值，则

\[\hat{y} = \hat{b}x+\hat{a} \]

称为 \(y\) 关于 \(x\) 的回归直线方程，对应的直线就称为回归直线。因为是使得残差平方和最小，所以其中涉及的方法称为最小二乘法。

这其中，残差的定义是当 \(x=x_i\) 时，\(e_i=y_i-\hat{y}_i\) 的值。

这其中，\(\hat{b}\) 和 \(\hat{a}\) 的求法如下：

\[\hat{b} = \frac{\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)}{\sum_{i=1}^n(x_i-\bar x)^2} = \frac{\sum_{i=1}^nx_iy_i-n\bar x\bar y}{\sum_{i=1}^nx_i^2 - n\bar x^2} \]

\[\hat{a} = \bar y - \hat{b}\bar x \]

其中 \(\bar x\) 即 \(x_i\) 的平均数，\(\bar y\) 即 \(y_i\) 的平均数。

性质

\((1)\)： 回归直线一定过点 \((\bar x,\bar y)\)，这个只需要把 \(\hat{a}\) 的定义式带回去即可证明。这个点叫做样本中心；

\((2)\)：残差绝对值越小，回归直线的拟合程度越高；

\((3)\)：一次函数 \(\hat{y} = \hat{b}x+\hat{a}\) 的单调性显然是由 \(\hat{b}\) 的符号决定的，函数递增的充要条件是 \(\hat{b} > 0\)，这说明：\(y\) 与 \(x\) 正相关的充要条件是 \(\hat{b} > 0\)；\(y\) 与 \(x\) 负相关的充要条件是 \(\hat{b} < 0\)。

\((4)\)：当 \(x\) 增大 \(1\) 个单位时，\(\hat{y}\) 增大 \(\hat{b}\) 个单位，这个显然。

相关系数

相关系数 \(r\) 是用来刻画 \(x\) 和 \(y\) 的线性相关性强弱的，它的公式是

\[r = \frac{\sum_{i=1}^n(x_i-\bar x)(y_i-\bar y)}{\sqrt{\sum_{i=1}^n(x_i-\bar x)^2\sum_{i=1}^n(y_i-\bar y)^2}} = \frac{\sum_{i=1}^nx_iy_i-n\bar x\bar y}{\sqrt{(\sum_{i=1}^nx_i^2-n\bar x^2)(\sum_{i=1}^ny_i^2-n\bar y^2)}} \]

它的平方用 \(R^2\) 表示，也有一个公式

\[R^2 = 1-\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\sum_{i=1}^n(y_i-\bar y)^2} \]

可以看出，下面是个定值，分子就是残差的平方和。

相关系数有如下性质：

\((1)\)： \(R^2\) 越大，或者说 \(|r|\) 越大，线性相关性越强；

\((2)\)：\(|r|\leq 1\)，且 \(y\) 与 \(x\) 正相关的充要条件是 \(r > 0\)，\(y\) 与 \(x\) 负相关的充要条件是 \(r<0\)；

\((3)\)：\(|r|=1\) 的充要条件是成对数据构成的点都在回归直线上。

\((4)\)：一般地，如果 \(|r| \ge 0.75\)，则说明这两个变量线性相关性较强；如果 \(|r|<0.75\)，则说明这两个变量线性相关性较弱。

注意了，\(r=0\) 只能说明 \(y\) 和 \(x\) 没有线性相关关系，并不是没有相关关系。

非线性回归

通法：把非线性回归变成线性回归。

---

例: \(y=Me^{Nx}\) 这个函数，是一个非线性回归方程。

两边取 \(\ln\) ：

\[\begin{aligned} \ln y&=\ln(Me^{Nx})\\ \ln y &=\ln M + Nx \end{aligned} \]

然后换元，设 \(Y = \ln y\)，原方程就变为了

\[Y = Nx + \ln M \]

其中，\(N\) 就是 \(\hat{b}\) ，\(\ln M\) 就是 \(\hat{a}\)，这就变成了一个线性回归方程。

独立性检验

列联表

形如

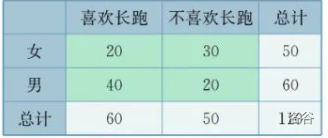
的表格，就叫做列联表。可以看出，重点是中间的 \(2\times2\) 的 \(4\) 个格子，所以这样的表格通常称为 \(2\times 2\) 列联表。

独立性检验

若记这四项分别是 \(a,b,c,d\)，定义

\[\chi^2 = \frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)} \]

其中 \(n=a+b+c+d\)，读作“卡方”。这个值就是用来衡量相关性大小的。

如果 \(\chi^2\) 越大，两个变量的相关性越强，相关性越强，也就说明它们之间的独立性越弱，所以用这个来检验独立性。

因为是根据样本得来的，所以 \(\chi^2\) 越大不一定没有独立性，只能说在这个样本下是这样的。

接下来给个标准，以此判断多大才说相关性强。

其中 \(\chi^2\) 就是图中的 \(k_0\)。而上面一行的数值是犯错概率。举个例子，如果你算出吸烟和肺癌的 \(\chi^2\) 是 \(10.828\)，那么就说明吸烟和肺癌有 \(99.9\%\) 的概率是相关的，只有 \(0.1\%\) 的概率是无关的。如果说 \(\chi^2\) 要比 \(10.828\) 还要大，那么就说么无关的概率更小了。

其中第一行的数我们称之为显著性水平，记作 \(a\)，它所对应的 \(k_0\) 我们就称之为显著性水平 \(a\) 对应的分位数，如果

\[P(\chi^2 \ge k) =a \]

那么就说明如果 \(\chi^2\) 的值 \(\ge k\)，那么就就有 \(a\) 的概率两个事件无关，\(1-a\) 的概率两个事件有关。这个过程就是我们所说的独立性检验。