初等数论(Ⅲ):高次同余相关
前言
关于高次同余方程,有 \(a^x \equiv b(\text{mod} \ p)\) 和 \(x^a \equiv b(\text{mod} \ p)\) 两种类型,后者计算起来较为麻烦,下文就分别记述这两种高次同余方程。
本文大多摘抄自 \(\text{Alex_Wei}\) 以及 微光理科。
离散对数问题
离散对数问题是在模 \(p\) 意义下求解 \(\log_ab\),这等价于形如
的高次同余方程,其中 \(x\) 即为 \(\log_ab\),\(x\) 是一个非负整数。
当 \(a \perp b\) 时,我们可以采用 BSGS 算法解决;当 \(a \not\perp b\) 时,可以采用 exBSGS 算法求解。
BSGS
大步小步算法,英文名为 Baby Step Giant Step,简称 BSGS。适用于 \(a\perp p\) 的情况。
算法流程
由扩展欧拉定理得
所以 \(a^x\) 模 \(p\) 意义下的循环节就是 \(\varphi(p)\),又因 \(\varphi(p) < p\),所以考虑 \(x\in[0,p]\) ,一定能找到最小整数 \(x\)。自此,问题缩小到了 \(O(p)\) 级别。如果 \(p\leq 2^{32}\),那就超时了。这时候就要请出我们今天的主角----根号平衡闪亮登场!
我们令 \(x = im-j\),其中 \(m=\lceil \sqrt{p} \ \rceil , i\in[1,m],j\in[0,m-1]\)。这样分配,\(im-j\) 就能取遍 \([1,p]\) 了,如果 \(x=0\),说明 \(b=1\),特判一下就行了。
我们把上式转换一下,则有
因为 \(a\perp p\) ,所以
是一个等价转换(除回去模数不变)。
然后枚举 \(i,j\)。
-
先枚举 \(j\),把 \((ba^j \ \text{mod} \ p,j)\) 插入一个 Hash 表。如果 \(ba^j \ \text{mod} \ p\) 出现相等的情况,为了求最小解,显然用更大的 \(j\) 替代小的解。
-
然后枚举 \(i\) ,计算 \((a^m)^i \ \text{mod} \ p\),到 Hash 表中判断是否有相等的 key,因为 \(i\times m\) 的变化量是比 \(j\) 大的,所以我们找到第一个就可以结束程序,最小的 \(x=im-j\) 就出来了。
这样,枚举 \(i,j\) 的次数都是 \(\sqrt p\) 的,总算法的复杂度也就是 \(O(\sqrt{p\ })\) 的。
map <int,int> Hash;
signed main()
{
mod = read() , a = read(), b = read();
if(b == 1) { return printf("0"),0; }//特判一下
m = ceil(sqrt(mod));
Hash[b] = 0/*j取0,ba^j就是b*/ , t = b;
for(re int i=1;i<m;i++)//枚举ba^j
{
t = t * a % mod;
Hash[t] = i;
}
val = ksm(a,m) , t = 1;
for(re int i=1;i<=m;i++)//枚举(a^m)^i
{
t = t * val % mod;
if(Hash.count(t)) { return printf("%lld",i*m-Hash[t]),0; }//有值直接输出
}
printf("no solution");
return 0;
}
实际上,如果 \(a\perp p ,a^x \equiv b(\text{mod} \ p)\) 的 \(x\) 存在,则有循环节 \(\delta_p(a)\) ,证明就是把 \(x\) 分解成 \(q\delta_p(a) + r\) ,然后前面的与 \(1\) 同余就完了,具体详见下文阶有关。
exBSGS
当 \(a\not\perp p\) 的时候,我们的 exBSGS 就要出场了。
化未知为已知,我们思考怎么操作能让 \(a,p\) 互质。
首先,原方程可以写作
的形式,这就是把 \(a\) 提出来的一个过程。这也等价于求 \(a\cdot a^{x-1} + py = b\) 的解。
令 \(d_1 = \gcd(a,p)\)。如果 \(d_1\nmid b\),则原方程无解。
否则由同余的性质得,同余方程就变成
这启发我们要不断提取 \(a\) 出来,直到 \(a\) 和模数互质。
设 \(d_2 = \gcd(a,\frac{p}{d_1})\),然后重复上述操作,直到互质。
当 \(a\perp \frac{p}{d_1\dots d_k}\) 时,我们就可以套用 BSGS 了。设 \(D = \prod_{i=1}^kd_i\),原方程就变成了形如
的形式。因为 \(a\perp \frac{p}{D}\),所以 \(\frac{a^k}{D}\perp \frac{p}{D}\),那么就可以求个逆元,把 \(\frac{a^k}{D}\) 消掉,然后再套一个 BSGS 就可以了。
注意,BSGS 结束后算出来的是 \(x-k\) 而非 \(x\),别忘了把 \(k\) 加上。
实际上,\(\frac{a^k}{D}\) 也可以不用求逆元,只要在 BSGS 枚举 \(i\) 的时候把初值设为 \(\frac{a^k}{D}\) 即可。
code
il int BSGS(int a,int b,int mod,int k)
{
Hash.clear();
m = ceil(sqrt(mod));
Hash[b] = 0 , t = b;
for(re int i=1;i<m;i++)
{
t = 1ll * t * a % mod;
Hash[t] = i;
}
val = ksm(a,m,mod) , t = k;//初值设为k
for(re int i=1;i<=m;i++)
{
t = 1ll * t * val % mod;
if(Hash.count(t)) { return i*m-Hash[t]; }
}
return -1;
}
il void exBSGS()
{
a = read() , mod = read() , b = read();
if(!a && !mod && !b) exit(0);
a %= mod , b %= mod;//先模再特判
if(b == 1 || mod == 1) { puts("0"); return ; }
cnt = d = 0 , k = 1;
while((d=gcd(a,mod)) != 1)
{
if(b % d) { puts("No Solution"); return; }//无解情况
cnt++;//不知道为什么这个放在if上面就wa一个点,很怪
b /= d , mod /= d;//逐渐往下找
k = 1ll * k * (a / d) % mod;//a^{x-k}前的系数
if(k == b) { printf("%d\n",cnt); return ; }//k==b说明a^{x-k} = 1,x=k
}
ans = BSGS(a,b,mod,k);
if(ans == -1) puts("No Solution");
else printf("%d\n",ans+cnt);
}
阶和原根
模 \(n(n>1)\) 的缩系在模 \(n\) 乘法意义下封闭且符合群的定义,构成一个群。这个群满足封闭性和结合性,且存在逆元和单位元。将群的定义套在这个群里,就能得出相关的定义。
阶
定义:设 \(n\) 为正整数,对于模 \(n\) 缩系里的任意一个元素 \(a\),我们有欧拉定理。
因此,对于缩系中的任意一个元素 \(a\),方程
一定有整数解,\(x=\varphi(n)\) 就是其中一解。
在 \(a^x \equiv 1(\text{mod} \ n)\) 的所有正整数解中,一定有一个最小的,这个最小的正整数 \(x\) 被称为 \(a\) 模 \(n\) 的阶,记作 \(\delta_n(a)\)。
易知 \(a\perp n\) 是 \(\delta_n(a)\) 存在的充要条件。
充分性:若 \(a\perp n\),由欧拉定理知存在一个解为 \(x=\varphi(n)\),阶存在。
必要性:若 \(a \not\perp n\),则 \(a^x \not\perp n\),那么 \(a^x\) 模 \(n\) 不可能等于 \(1\)。
为什么要求阶?这里引用 \(\text{Alex_Wei}\)的话。
阶就是将一个数自乘若干次后模 \(n\),第一次得到 \(1\) 的自乘次数。之所以是得到 \(1\),是因为 \(1\) 的性质很好。例如它和所有数互质,且 \(1\) 的任何次幂均为 \(1\),且 \(1\) 是 \(1\) 在模任何正整数意义下的乘法逆元,因此我们可以在同余方程的任意位置除以已经被证明等于 \(1\) 的部分,而不需要担心不存在逆元。
阶的性质
性质1:\(a^x \equiv 1(\text{mod}\ n)\) 成立当且仅当 \(\delta_n(a) \mid x\)。
证明:设 \(d=\delta_n(a)\),则 \(x=qd+r\),其中 \(0\leq r < d\)。因为 \(d\) 是最小的 \(x\),所以 \(q \ge1\)。则有
所以说 \(a^r \equiv 1(\text{mod}\ n)\),又因为 \(r<d\) ,\(d\) 是最小的,所以 \(r\) 只能为 \(0\)。所以 \(x = qd\),一定是 \(d\) 的倍数。
推论1:对于任意一个模 \(n\) 缩系中的 \(a\),都有 \(\delta_n(a) \mid \varphi(n)\)。
这个由性质 \(1\) 可以显然看出来。
性质2:
- 对于有 \(\gcd\) 的这个式子,证明如下:
我们设 \(\delta_n(a) = t\)(目的是为了好看一点)。
那么则有
这一步的目的是先证明 \(a^x \equiv 1\),再证明它是最小的。
我们再设 \(s = \delta_n(a^k)\),根据性质 \(1\),我们可以知道 \(s \mid \frac{t}{\gcd(t,k)}\)。
再把 \(a\) 当成底数,再根据性质 \(1\),可以得出 \(t \mid ks\),则有 \(\frac{t}{\gcd(t,k)}\mid s\)(这个性质可以分解质因数简单证明一下)。
所以 \(s = \frac{t}{\gcd(t,k)}\),即 \(\delta_n(a^k) = \frac{\delta_n(a)}{\gcd(\delta_n(a),k)}\)。证毕。
-
对于有 \(\text{lcm}\) 的这个式子,因为能够整除 \(k\) 的最小的 \(\delta_n(a)\) 的倍数为 \(\text{lcm}(\delta_n(a),k)\)。为什么要求这个?因为这个数同时同时满足 \(\delta_n(a)\mid \text{lcm}(\delta_n(a),k)\) 和 \(\delta_n(a^k)\mid \text{lcm}(\delta_n(a),k)\)(性质 \(1\)),并且是最小的。所以使得 \(a^{kx} \equiv 1(\text{mod} \ n)\) 的最小的 \(kx=\text{lcm}(\delta_n(a),k)\),所以 \(x_{\min} = \frac{lcm(\delta_n(a),k)}{k}\)。
-
实际上你只要推出来一个式子,就可以通过 \(a\times b = \gcd(a,b) \times \text{lcm}(a,b)\) 得出。
求解 \(\delta_n(a)\)
保证 \(a\perp n\)。
\(\text{Method 1}\):直接用 BSGS 求 \(a^x \equiv 1(\text{mod} \ n)\) 的最小整数解。时间复杂度 \(O(\sqrt n)\).
\(\text{Method 2}\):根据性质 \(1\) ,对于 \(x=k\delta_n(a)\) ,必然有 \(a^x \equiv 1(\text{mod} \ n)\)。因此首先考虑 \(a=\varphi(n)\),则答案一定是 \(\varphi(n)\) 的因数。将其质因数分解,然后挨个试。
单次询问时间复杂度就是 \(O(\sqrt n + \log^2n)\),来源于分解质因数的 \(O(\sqrt n)\) 和求解欧拉函数完枚举质因数和快速幂合起来的 \(O(\log^2n)\)。
用 Pollard-rho 分解质因数可以做到 \(O(n^{\frac{1}{4}})\)。如果 \(n\) 不大,并且多组询问,可以 \(O(n)\) 线性筛筛出欧拉函数以及每个数的最小质因数,这样单次询问的复杂度就是 \(O(\log^2n)\) 的了,总复杂度就是 \(O(n+q\log^2n)\)。
原根
定义
如果对于正整数 \(a,n\),\(a\perp n\) 且 \(\delta_n(a) = \varphi(n)\),那么 \(a\) 就称为模 \(n\) 的原根。
并不是所有的数都有原根。存在原根的模 \(n\) 缩系同构于循环群,所以原根这一概念等价于循环群中的生成元,由它一个可以生成这个群里所有的元素。
定理
原根判定定理:对于 \(n \ge 3\),\(a\perp n\),\(a\) 是 \(n\) 的原根的充要条件是对于任意 \(\varphi(n)\) 的质因子 \(p\),均有 \(a^{\frac{\varphi(n)}{p}} \not \equiv 1\)。
证明:
必要性:比较显然,把 \(\varphi(n)\) 的所有真因子取遍了模 \(n\) 都不等于 \(1\),有根据欧拉定理得,\(a^{\varphi(n)} \equiv 1(\text{mod} \ n)\),所以 \(\varphi(n)\) 就是最小的满足 \(a^x\equiv 1(\text{mod} \ n)\) 的条件的数,\(\varphi(n)\) 就是 \(a\) 模 \(n\) 的阶。
充分性:因为 \(\frac{\varphi(n)}{p}\) 取遍了 \(\varphi(n)\) 的真因子。假设存在 \(d\) 使得 \(a^d \equiv 1(\text{mod} \ n)\) 且 \(d < \varphi(n)\),由阶的性质得 \(d\mid \varphi(n)\),则必存在质因子 \(p\) 满足 \(d\mid \frac{\varphi(n)}{p}\),这说明存在 \(a^{\varphi(n)}{p}\equiv 1(\text{mod} \ n)\),与假设矛盾。证毕。
原根存在定理:一个数 \(n\) 存在原根的充要条件是 \(n=2,4,p^{\alpha},2p^{\alpha}\),其中 \(p\) 是奇质数。
证明过于复杂,故略,我选择记住/cy。
原根作为生成元的性质:设 \(g\) 为模 \(n\) 的原根,则 \(g,g^2,g^3,\dots,g^{\varphi(n)}\),这 \(\varphi(n)\) 个数构成模 \(n\) 的缩系。
证明:
如果 \(1\leq i \leq j \leq \varphi(n)\) 满足
因为 \(\gcd(g,n) = 1\),因此 \(\gcd(g^i,n) = 1\),则有
又因为 \(g\) 是模 \(n\) 的原根,\(\delta_n(g) = \varphi(n)\),根据阶的定理 \(1\),则有
又因为 \(0\leq j-i < \varphi(n)\)。所以 \(j-i \) 只能为 \(0\),即 \(j=i\)。
从而 \(g,g^2,g^3,\dots,g^{\varphi(n)}\) 模 \(n\) 互不同余,这 \(\varphi(n)\) 个数都和 \(n\) 互质,所以它们组成了模 \(n\) 的缩系。
原根个数定理:如果正整数 \(n\) 有原根 \(g\),那么模 \(n\) 有 \(\varphi(\varphi(n))\) 个原根,这些原根可以写成 \(g^u\),其中 \(u\) 是 \(1\sim\varphi(n)\) 中与 \(\varphi(n)\) 互质的数。
证明:
因为 \(\delta_n(g) = \varphi(n)\),根据阶的性质 \(2\),就能得到
当且仅当 \(\gcd(\varphi(n),u) = 1\) 时,上式的值为 \(\varphi(n)\),即当且仅当 \(\gcd(\varphi(n),u) = 1\) 时,\(g^u\) 也是模 \(n\) 的原根。
也就是说,和 \(\varphi(n)\) 互质的数有 \(\varphi(\varphi(n))\) 个,\(g\) 的这些数的幂次就都是模 \(n\) 的原根。
求原根
-
(一)预处理
-
- 线性筛筛一下质数和欧拉函数值,并且存一下每个数的最小质因子。
-
- 预处理出有原根的数的个数,运用原根存在定理往后枚举就行了。
预处理的复杂度是 \(O(n)\) 的。
-
-
(二)求最小原根
-
- 从小到大枚举 \(g\) 并检验是否是 \(n\) 的原根即可,已经证明了这个 \(g\) 是 \(O(n^{0.25+\varepsilon})\) 级别的,所以直接枚举即可。
-
- 对于每个 \(g\),通过原根判定定理来做,由于已经筛出了最小质因数,所以这个枚举的复杂度是 \(O(n^{0.25}\omega(n)\log n)\) 的。
-
-
(三)求全部原根
- 1.运用原根个数定理,判定一下 \(i\) 是否和 \(\varphi(n)\) 互质,如果互质,那么 \(g^i\) 也是一个原根,这样枚举的复杂度就是 \(O(\varphi(n)\log\varphi(n))\) 的。
code
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e6 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
bool isprime[N],root[N];
int phi[N],prime[N],ans[N],fac[N];
int T,n,d,cnt,cntans,tot,minroot;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il int gcd(int a,int b) { return b ? gcd(b,a%b) : a; }
il int ksm(int a,int b,int mod)
{
int res = 1;
while(b)
{
if(b&1) res = 1ll * res * a % mod;
a = 1ll * a * a % mod;
b >>= 1;
}
return res;
}
il void get_phi(int n)
{
memset(isprime , 1 ,sizeof isprime);
isprime[1]=0; phi[1] = 1;
for(int i=2;i<=n;i++)
{
if(isprime[i])
{
prime[++cnt]=i;
phi[i] = i-1;//情况1
}
for(int j=1;j<=cnt && prime[j]*i <=n ;j++)
{
int m = i*prime[j];
isprime[m]=0;
if(i%prime[j] == 0)
{
phi[m] = prime[j] * phi[i];//情况2
break;
}
else phi[m] = (prime[j]-1)*phi[i];//情况3
}
}
root[2] = root[4] = 1;
for(re int i=2;i<=cnt;i++)
{
for(re int j=1;(1ll*j*prime[i])<=N-5;j*=prime[i]) root[j*prime[i]] = 1;
for(re int j=2;(1ll*j*prime[i])<=N-5;j*=prime[i]) root[j*prime[i]] = 1;
}
}
il void Decompose(int x)
{
for(re int i=2;i*i<=x;i++)
{
if(x % i == 0)
{
fac[++tot] = i;
if(x % i == 0) x /= i;
}
}
if(x > 1) fac[++tot] = x;
return ;
}
il bool check(int x,int p)
{
if(ksm(x,phi[p],p) != 1) return 0;//满足欧拉定理先
for(re int i=1;i<=tot;i++)
if(ksm(x,phi[p]/fac[i],p) == 1) return 0;//因数不能为1
return 1;
}
il int Get_Minroot(int p)
{
for(re int i=1;i<p;i++)//暴力枚举1-n找n的原根
if(check(i,p)) return i;
return 0;
}
il void Get_Allroot(int x,int p)
{
int mul = 1;
for(re int i=1;i<=phi[p];i++)
{
mul = (1ll * mul * x) % p;
if(gcd(i,phi[p]) == 1) ans[++cntans] = mul;
}
return ;
}
il void Main()
{
n = read() , d = read();
if(root[n])
{
tot = cntans = 0;
Decompose(phi[n]);//分解phi[n],预处理出其质因数
minroot = Get_Minroot(n);//找最小原根
Get_Allroot(minroot,n);//找所有原根
sort(ans+1,ans+cntans+1);
cout << cntans << "\n";
for(re int i=1;i<=cntans/d;i++) cout << ans[i*d] << " ";
puts("");
}
else puts("0\n");
}
signed main()
{
get_phi(N-5);
T = read();
while(T--) Main();
return 0;
}
原根的另一个重要性质
若 \(n\) 存在原根 \(g\),设 \(m=\varphi(n)\) ,则 \(n\) 的缩系与 \(m\) 次单位根同构(换个名字,本质不变)。
由原根作为生成元的性质可以得到,对于任何一个 \(a \perp n\),其都能写成 \(g^k\) 的形式,而任何一个 \(n\) 次单位根也能写成 \(\omega_1^k\) 的形式。同时,\(g^k \equiv 1(\text{mod} \ n)\),并且 \(\omega_1^k = 1\)。因此我们可以将单位圆应用到 \(n\) 的缩系上,形象地表示出原根的性质。
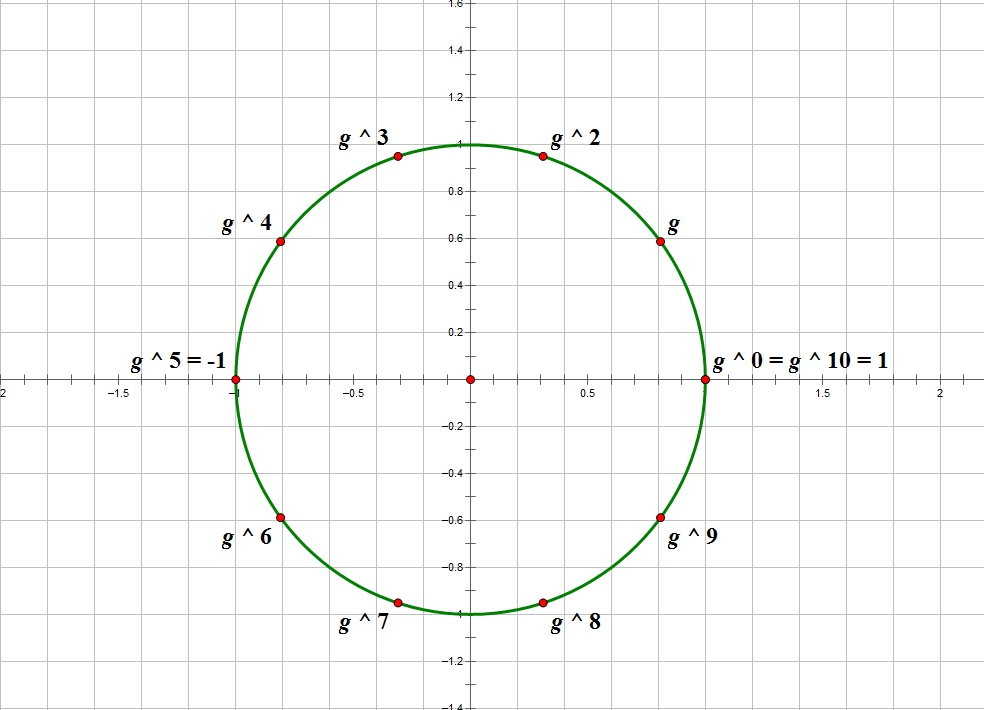
如图,单位根的运算是 \(\omega_i \times \omega_j = \omega_{(i+j)\bmod 10}\),而这就对应着原根的 \(g^i \times g^j \equiv g^{(i+j)\bmod 10}(\bmod \ 11)\),圆环上的运算的循环往复体现出来的就是模操作。
这就是为什么对于特定模数,我们可以使用原根代替 \(n\) 次单位根进行快速傅里叶变换: \(\varphi(998244353) = 2^{22} \times 238\),所以当需要用 \(2^k\) 次单位根的时候,若 \(k\) 不超过 \(\varphi(p)\) 中质因子 \(2\) 的个数且存在原根,即可用原根代替 \(2^k\) 次单位根,这就是快速数论变化 NTT。
高次剩余
若 \(b\) 在模 \(p\) 意义下能表示成某个数 \(x\) 的 \(a\) 次方,即
则称 \(b\) 为模 \(p\) 意义下的 \(a\) 次剩余。
由于我太菜了,只会二次剩余,所以这部分其实主要讲的是二次剩余。
二次剩余
定义与符号
二次剩余与二次非剩余:由定义得,若存在 \(x\) 使得 \(x^2 \equiv n(\bmod \ p)\),则称 \(n\) 为模 \(p\) 的二次剩余,反之则称 \(n\) 为模 \(p\) 的二次非剩余。
需要注意的一点是,这个定义是建立在 \(n\) 不是 \(p\) 的倍数的基础上的,也就是说如果 \(n\) 是 \(p\) 的倍数,那么 \(n\) 既不是模 \(p\) 的二次剩余,也不是模 \(p\) 的二次非剩余。
勒让德符号:为了简便表示上述的情况,我们引入勒让德符号:
欧拉准则
用于判定 \(n\) 是否是模 \(p\) 意义下的二次剩余。
以下讨论都是基于 \(p\) 是奇素数的情况展开的。对于任意模数二次剩余,我们有:
什么?怎么会有出题人毒瘤到考这种玩意?
当 \(p\) 为奇素数并且与 \(n\) 互质时,根据费马小定理,我们有
由于 \(p-1\) 是一个偶数,则有
移项,得
所以,当 \(p\) 为奇素数且与 \(n\) 互质时,\(n^{\frac{p-1}{2}}\) 在模 \(p\) 意义下只可能等于 \(1\) 或 \(-1\)。
欧拉准则给出公式。
也就是说,当 \(n^{\frac{p-1}{2}} \equiv 1(\bmod \ p)\) 时,\(n\) 是模 \(p\) 的二次剩余,\(\equiv -1\) 时,\(n\)就是模 \(p\) 的二次非剩余。
这就有了一个结论:
\(n\) 是模 \(p\) 的二次剩余是 \(n^\frac{p-1}{2}\equiv 1(\bmod \ p)\) 的充要条件。
证明:
充分性:当 \(x^2 \equiv n(\bmod \ p)\) 成立时,则有
证毕。
必要性:因为 \(p\) 是一个奇素数,所以一定存在原根。设 \(g\) 是模 \(p\) 的一个原根。所以设 \(n = g^k\)。根据原根的定义,\(g^{\frac{p-1}{2}}\not\equiv 1\),故 \(g^{\frac{p-1}{2}} \equiv -1(\bmod \ p)\)。所以
所以 \(k\) 是偶数,因此就有
即 \(a\) 为二次剩余。
证毕。
既然这两个互为充要条件,那就代表着 \(n^{\frac{p-1}{2}} \equiv -1(\bmod \ p)\) 对应着 \(n\) 是模 \(p\) 的非二次剩余,剩下一种倍数的也是对的,这样欧拉准则就证明完毕了。
解的数量
对于方程 \(x^2 \equiv n(\bmod \ p)\) 来说,取其不相等的两个解 \(x_1\) 和 \(x_2\) ,那么对于 \(x_1,x_2\) 有:
因为 \(x_1\not=x_2\),所以 \(x_1-x_2\) 不能为 \(0\),所以只能是 \(x_1+x_2 \equiv 0(\bmod \ p)\),又因为 \(p\) 是奇数,所以说 \(x_1\) 和 \(x_2\) 在模 \(p\) 意义下互为相反数且奇偶性相反。
这也就是说,一个二次剩余对应一对模意义下的不同的相反数。因为模 \(p\) 意义下能找到 \(\frac{p-1}{2}\) 对非零的相反数,所以在模 \(p\) 意义下共有 \(\frac{p-1}{2}\) 个二次剩余,对应的,也就有 \(\frac{p-1}{2}\) 个二次非剩余。
求解二次同余-Cipolla算法
Cipolla 算法适用于解模数是奇素数的情况。
流程如下:
首先 Cipolla 算法实际上是一个模意义下扩域的过程,将整数域扩为整系数复数域。这就类似于从实数域扩张到复数域一样。
-
先找到一个 \(a\) 使得 \(a^2-n\) 是二次非剩余,令 \(i^2 \equiv a^2-n(\bmod \ p)\),则 \((a+i)^{\frac{p+1}{2}}\) 即是方程的一个解,其相反数就是另一个解。
这里的 \(i\) 就是我们引出的这个复数域的虚数单位,因为在实数域中这个是二次非剩余,是无解的,但扩域一下,就有了。
其实就这一步就做完了,我们考虑如何去证明这个结论:
其中,第一步到第二步可以见证明我这篇博客中证明 Lucas 定理的那一部分。
第二步到第三步:由费马小定理得 \(a^p\equiv a(\bmod \ p)\),而
后面的都比较显然了。
既然 \((a+i)^{p+1} \equiv 1(\bmod \ p)\),那么 \((a+i)^{\frac{p+1}{2}}\) 自然是方程的一个解了,对于这个解取相反数就是另一个解了。
运用二项式定理展开,可以证得 \((a+i)^{p+1}\) 的虚部一定为 \(0\),这就保证了解一定是在整数域里面的。
具体的实现过程就是在 \(0\sim p\) 中随机一个 \(a\),运用欧拉准则判断 \(a^2-n\) 是否是非二次剩余,因为非二次剩余的个数是 \(\frac{p}{2}\) 的,期望 \(2\) 次就找完了。总的复杂度就是快速幂的 \(O(\log p)\)。
code
int T,w,n,mod,ans1,ans2,a;
struct Complex{
int x,y;
}x;
Complex operator *(Complex a,Complex b)
{
Complex res;
res.x = ((a.x*b.x%mod)+(a.y*b.y%mod*w)%mod + mod) % mod;
res.y = ((a.x*b.y%mod)+(a.y*b.x%mod)+ mod) % mod;//复数乘法运算
return res;
}
il int ksm(int a,int b)
{
int res = 1;
while(b)
{
if(b&1) res = res * a % mod;
a = a * a % mod;
b >>= 1;
}
return res % mod;
}
il int cksm(Complex a,int b)
{
Complex res = {1,0};
while(b)
{
if(b&1) res = res * a;
a = a * a;
b >>= 1;//复数域上的快速幂
}
return res.x;//因为虚部为0,只用返回实部
}
il int cipolla()
{
n %= mod;
if(ksm(n,(mod-1)/2) == mod-1) return -1;
while(1)
{
a = rand() % mod;//随机用欧拉准则找
w = ((a*a%mod-n)%mod + mod) % mod;//a^2-n
if(ksm(w,(mod-1)/2) == mod-1) break;
}
x = {a,1};
return cksm(x,(mod+1)/2);
}
il void Main()
{
srand(time(NULL));
n = read() , mod = read();
if(!n) { puts("0"); return ; }//n等于0,答案显然为0
ans1 = cipolla() % mod, ans2 = -ans1 + mod;//找两个解
if(ans1 == -1) { puts("Hola!"); return ; }
if(ans1 > ans2) swap(ans1,ans2);
if(ans1 == ans2) cout << ans1 << "\n";
else cout << ans1 << " " << ans2 << "\n";
}
signed main()
{
T = read();
while(T--) Main();
return 0;
}


