P4557 [JSOI2018]战争 题解
闵可夫斯基和
前言
入门建议看吉老师(吉如一)的计算几何入门到放弃。感觉应该是讲的最通俗易懂的了。
本文借鉴了Winxp的博客,以及吉老师视频中的思路。
写这篇博客的初衷是因为我作为一个初学者,此题里的题解对我来说理解起来不算太难,但是实现起来细节比较多,题解里也没有很详细地去解释(可能是因为我太菜了)。所以写这篇博客详细地解释一下这道题目里的一些操作。
定义
两个图形(也就是点集) \(A,B\) 的闵可夫斯基和定义为 \(C = \{a+b\mid a\in A,b\in B\}\)。
画一画图可以看出,闵可夫斯基和形成的图形就是一个图形 \(A\) 绕着图形 \(B\) 转一圈。
给个典图。
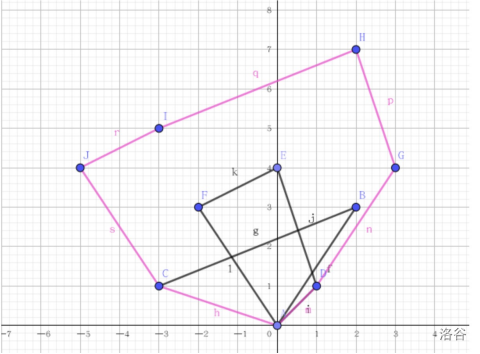
由于我比较菜,所以我们只考虑凸包的闵可夫斯基和的一些性质。
性质
一、
两个凸包的闵可夫斯基和还是凸包。
证明:
考虑凸集的一个性质:若 \(a,b\in A\),则 \(c = xa+(1-x)b ,c\in A(0\leq x \leq 1)\)。
设 \(a_1,a_2\in A,b_1,b_2 \in B\) ,根据闵可夫斯基和的定义,\(a_1+b_1,a_2+b_2\in C\)
任取一个
证毕。
二、
闵可夫斯基和上的边是由两个凸包的边构成的
这个不好证,但是我们用瞪眼法看一看,应该是对的。
有了这两个性质,我们就能求闵可夫斯基和了。
求法
思路比较简单,但是细节比较多。
因为我们得到 \(A,B\) 两个凸包后,它们的极角序其实是已经排好了的,所以我们就可以采用类似于归并排序的策略,将两个凸包结合起来。
得到闵可夫斯基和后,因为有可能会出现三点共线的情况,所以要再求一次凸包。
il void Minkovski()
{
for(re int i=1;i<n;i++) a[i] = s[i+1] - s[i]; a[n] = s[1] - s[n];//s是A凸包
for(re int i=1;i<m;i++) b[i] = h[i+1] - h[i]; b[m] = h[1] - h[m];//h是B凸包
int p1 = 1 , p2 = 1;
tot = 1 , G[tot] = s[1] + h[1];//归并加入一下,G数组就是闵可夫斯基和
while(p1 <= n && p2 <= m) tot++ , G[tot] = G[tot-1] + (a[p1]*b[p2]>=0 ? a[p1++]:b[p2++]);//极角序从小到大并从G[tot-1]开始往后接
while(p1 <= n) tot++ , G[tot] = G[tot-1] + a[p1++];
while(p2 <= m) tot++ , G[tot] = G[tot-1] + b[p2++];
}
我们用类似 a[i] = s[i+1]-s[i] 的操作得出每条边。再以 s[1]+h[1] 为起点开始往后加,每次加的时候就以 G[tot-1] 为基础往后接上。
应用
一句话题意。
给定两个凸包 \(A,B\),\(q\) 次询问,每次给出一个向量 \(\overrightarrow{x}\),问 \(B\) 平移向量 \(\overrightarrow{x}\) 后,\(A\) 和 \(B\) 是否还有交集。\(n,m,q \leq 10^5\)。
原题上领地是看三角形内部的区域,实际上就是凸包。而问是否有交集,数学化后就有了下面的式子:
如果有交,那么
转化一下,则有
我们看到这个很像 \(A,B\) 的闵可夫斯基和的形式,但是它们是相减,怎么办?把 \(B\) 取反,就变成闵可夫斯基和的形式了。
按照上述过程求出闵可夫斯基和后,接下来就剩下最后一个问题,如果判断一个点是否在凸包内,这个也比较好算,以图为例:
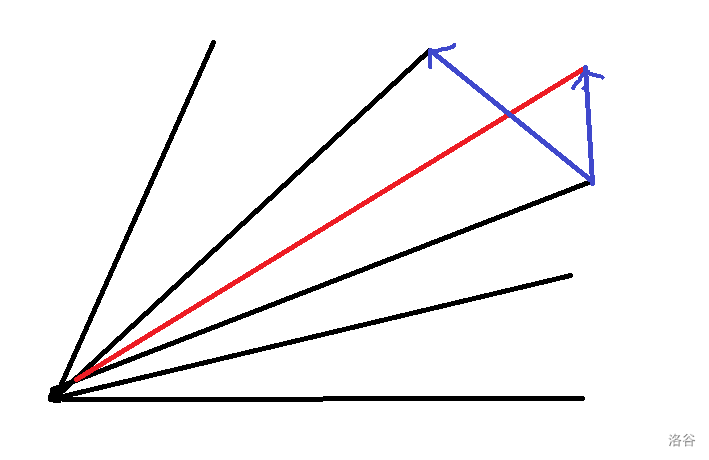
我们选定凸包上最左下角的点为起点,并将这个凸包平移一下,使得左下角的点坐落在原点上。这样就容易得出其他点的极角序了,我们按极角序进行二分,找到当前这个点与起点的连线位于哪两条线(凸包上的点与起点的连线)之间。然后如图连两条线,运用叉积运算判断这个点是在凸包外还是在凸包内即可。
另外还有一些小细节,我会在代码中写清。
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1e5 + 5;
const double eps = 1e-6;
const double Pi = acos(-1.0);
using namespace std;
struct Point{
double x,y;
}a[N],b[N],s[N],h[N],A[N],G[N],d,st;
int n,m,q,tot;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
Point operator +(Point a,Point b) { return Point{a.x+b.x,a.y+b.y}; }//加
Point operator -(Point a,Point b) { return Point{a.x-b.x,a.y-b.y}; }//减
il double operator *(Point a,Point b) { return a.x*b.y - a.y*b.x; }//叉积
il double operator &(Point a,Point b) { return a.x*b.x + a.y*b.y; }//点积
il double cross(Point a,Point b,Point c) { return (b-a)*(c-a); }//判断c和直线ab的关系
il double len(Point a) { return sqrt(a&a); }
il bool cmp(Point a,Point b) { return a.x == b.x ? a.y < b.y : a.x < b.x; }//以x为第一关键字,y为第二关键字排序
il bool cmp2(Point a,Point b) { return a*b > 0 || (a*b == 0 && len(a) < len(b)); }//按极角序排序,如果极角相同短的放前边
il void ConvexHull(Point *s,Point *p,int &n)//s是凸包数组,p是原数组
{
int cnt = 0;
sort(p+1,p+n+1,cmp);
s[++cnt] = p[1];
for(re int i=2;i<=n;i++) //Andrew求凸包
{
while(cnt > 1 && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
int t = cnt;
for(re int i=n-1;i>=1;i--)
{
while(cnt > t && cross(s[cnt-1],s[cnt],p[i]) <= 0) cnt--;
s[++cnt] = p[i];
}
n = cnt - 1;//第一个点加了两次,别忘了-1
}
il void Minkovski()
{
memset(a , 0 , sizeof a);
memset(b , 0 , sizeof b);//重复利用一下a,b数组,其实可以不memset
for(re int i=1;i<n;i++) a[i] = s[i+1] - s[i]; a[n] = s[1] - s[n];//最后一条线单独写一下
for(re int i=1;i<m;i++) b[i] = h[i+1] - h[i]; b[m] = h[1] - h[m];
int p1 = 1 , p2 = 1;
tot = 1 , G[tot] = s[1] + h[1];//以s[1]+t[1]为起点开始加
while(p1 <= n && p2 <= m) tot++ , G[tot] = G[tot-1] + (a[p1]*b[p2]>=0 ? a[p1++]:b[p2++]);
while(p1 <= n) tot++ , G[tot] = G[tot-1] + a[p1++];
while(p2 <= m) tot++ , G[tot] = G[tot-1] + b[p2++];
}
il bool Judge(Point a)
{
if(a*A[1] > 0 || A[tot]*a > 0) return 0;//绝对不可能在凸包内的情况
int pos = lower_bound(A+1,A+tot+1,a,cmp2) - A - 1;//lower_bound求的是第一个极角序不小于它的,所以减个1
return (a-A[pos])*(A[pos%tot+1]-A[pos])<=0;//如上文所说
}
signed main()
{
n = read() , m = read() , q = read();
for(re int i=1;i<=n;i++) scanf("%lf%lf",&a[i].x,&a[i].y);
for(re int i=1;i<=m;i++) scanf("%lf%lf",&b[i].x,&b[i].y) , b[i].x = -b[i].x , b[i].y = -b[i].y;
ConvexHull(s,a,n);
ConvexHull(h,b,m);
Minkovski();
ConvexHull(A,G,tot);
st = A[1];//选定一个基准点,并且把这个基准点平移到(0,0)的位置上,这样有利于我们求极角序
for(re int i=1;i<=tot;i++) A[i] = A[i] - st;//别的也减一下
while(q--)
{
scanf("%lf%lf",&d.x,&d.y);
printf("%d\n",Judge(d-st));//这个也别忘了减
}
return 0;
}
由此可以看出,整个复杂度是 \(O((n+m+q)\log(n+m))\) 的,\(n,m,q\) 同阶,复杂度也就是 \(O(n\log n)\),可以通过。


