Manacher

前言

以下内容大多摘抄自 董晓算法。

用途

Manacher 算法可以在 \(O(n)\) 的时间内求出一个字符串内以任意一个字符为中点的最大回文串长度。

前置芝士

• 回文半径：以 \(i\) 为中心的最长回文串长度的一半(包含自己)，叫回文半径，记作 \(d[i]\)。

  

• 加速盒子：我们不断维护一个右端点最靠右的一个最长的回文串，这个回文串包含的地方就被称为加速盒子。我们利用盒子以内的对称性从而快速转移 \(d[i]\) , 在盒子外我们进行朴素暴力。

  如上图，盒子就是方框框起来的区域。

算法流程

1.转化为奇回文串

因为 Manacher 只能找到长度为奇数的回文串，因此我们要在字符串之间和字符串两端插入一些特殊字符，使得其变成一个奇长度的串，好处理。另外，再在开头额外加一个特殊字符，防止越界。

Code:

具体如图

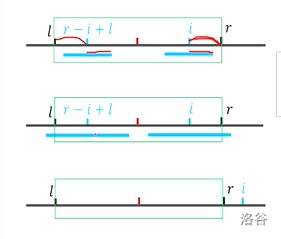
2.计算 \(d\) 值，扩展盒子\([l,r]\)

分类讨论一下

1.如果 \(i \leq r\)(在盒内)，那么 \(i\) 的对称点就为 \(r-i+l\)

• 若 \(d[r-i+l] < r-i+1\) , 由对称性可知， \(i\) 的最长回文串长度就那样了，已经固定了，直接转移即可。\(d[i] = d[r-i+l]\)

• 若 \(d[r-i+l] \ge r-i+1\) , 则说明到 \(r-i+1\) 的部分一定回文，但是由于盒子的右端点限于此了，无法确定后面的是否还是回文。这时候，我们令 \(d[i] = r-i+1\) ，从 \(r+1\) 往后暴力进行枚举。

2.如果 \(i > r\)(在盒外)，则从 \(i\) 开始暴力枚举

3.求出 \(d[i]\) 后，如果 \(i+d[i]-1 > r\) ，更新盒子为 \(l = i-d[i]+1,r=i+d[i]-1\)

代码实现

#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 1.1e7 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}

char a[N],ch[N<<1];
int d[N<<1];
int n,cnt,ans;
int l,r=1;

il int read()
{
	int f=0,s=0;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
	for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
	return f ? -s : s;
}

signed main()
{
	ios::sync_with_stdio(false);
	cin.tie(0); cout.tie(0);
	cin >> (a+1);
	ch[0] = '$' , ch[++cnt] = '#';
	n = strlen(a+1);
	for(re int i=1;i<=n;i++) ch[++cnt] = a[i] , ch[++cnt] = '#';
	n = cnt;
	d[1] = 1;
	for(re int i=2;i<=n;i++)
	{
		if(i <= r) d[i] = min(d[r-i+l],r-i+1);
		while(ch[i-d[i]] == ch[i+d[i]]) d[i]++;
		if(i+d[i]-1 > r) l = i-d[i]+1 , r = i+d[i]-1;
		ans = max(ans,d[i]);
	}
	cout << ans-1;
	return 0;
}