权值线段树

简介

权值线段树是一种建立在基本线段树之上的数据结构。因此它的基本原理仍是基于对区间的维护操作。但权值线段树维护的信息是：

一段区间内数出现的个数

实际上，权值线段树跟树状数组相似，都可以看作是一个桶。因此，根据权值线段树的性质，我们可以知道其主要用途：

求一段区间内数出现的次数、比 \(x\) 小的数的个数、比 \(x\) 大的数的个数、区间第 \(k\) 大的数、区间第 \(k\) 小的数。

权值线段树的基本原理与操作

1.权值线段树维护信息的原理

基础线段树和权值线段树的一个较大的区别点在于：

权值线段树不进行建树操作，初始状态下默认建立一棵所有点权为 \(0\) 的空树，对于每个元素，在遍历的时候相应的结点做自增运算。

所以我们可以看出，权值线段树的空间范围是视值域而定的，那么遇到 \(\leq 10^9\) 的值域后，我们就得采取 离散化或者是动态开点了(因为这个空间比较玄学，所以我们尽量在不爆的情况下开大一点)。

我们给定序列 \(\{1, 2, 2, 3, 3, 3, 4, 4, 4, 4 \}\)，以该序列为例建立权值线段树。

首先给一棵空树：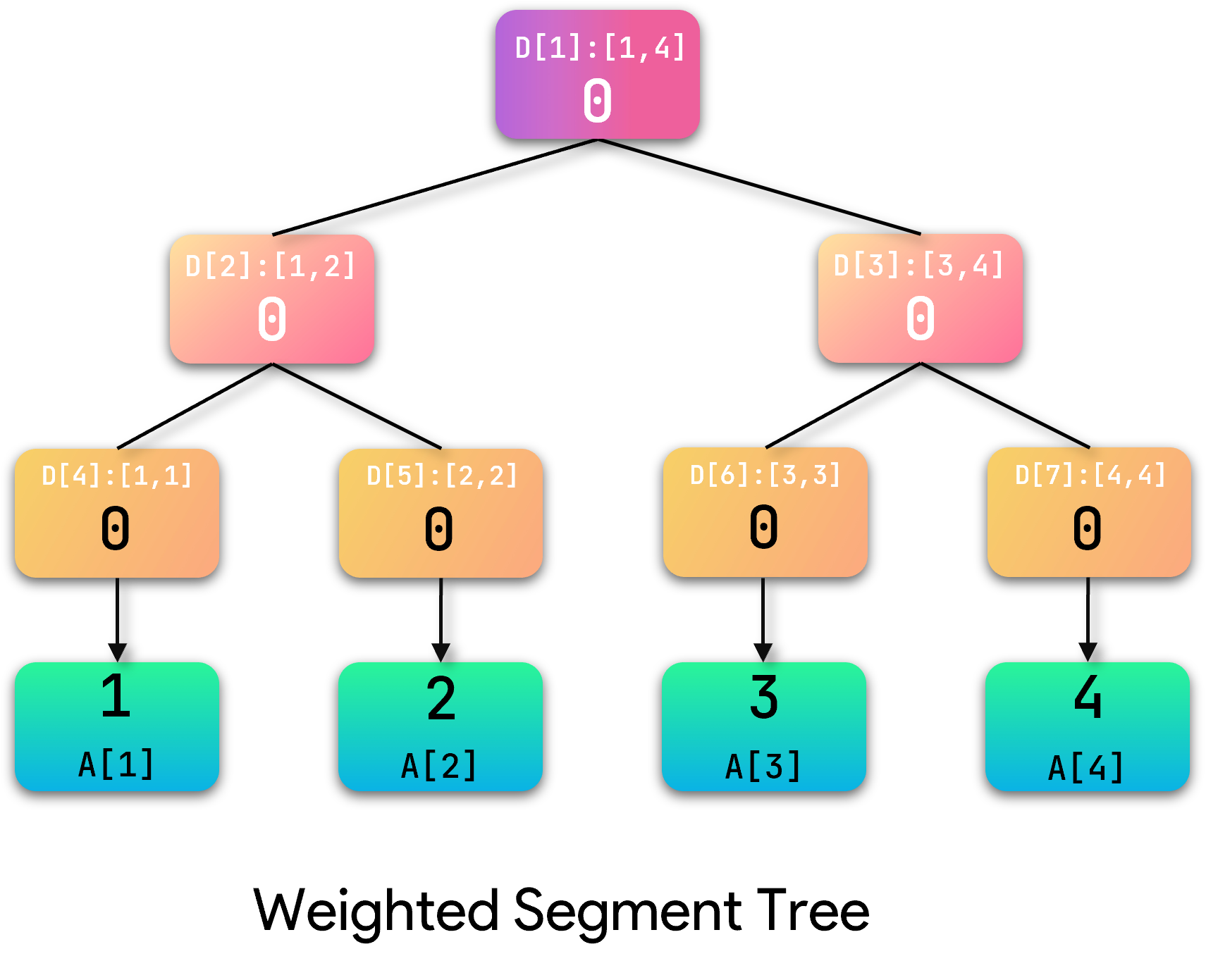

再按照顺序插入元素:

\(A[i]\) 表示原序列中存在值为 \(i\) 的元素的个数。

\(D[i]\) 表示一定区间内所含元素的个数

2.基本操作与实现

①.查询第 \(K\) 大/小元素

假设 \(K=5\)，这里查询第 \(K\) 大：

首先我们要知道，第 \(K\) 大是从右往左数的，是相对于终点而言的，所以从右子节点开始判断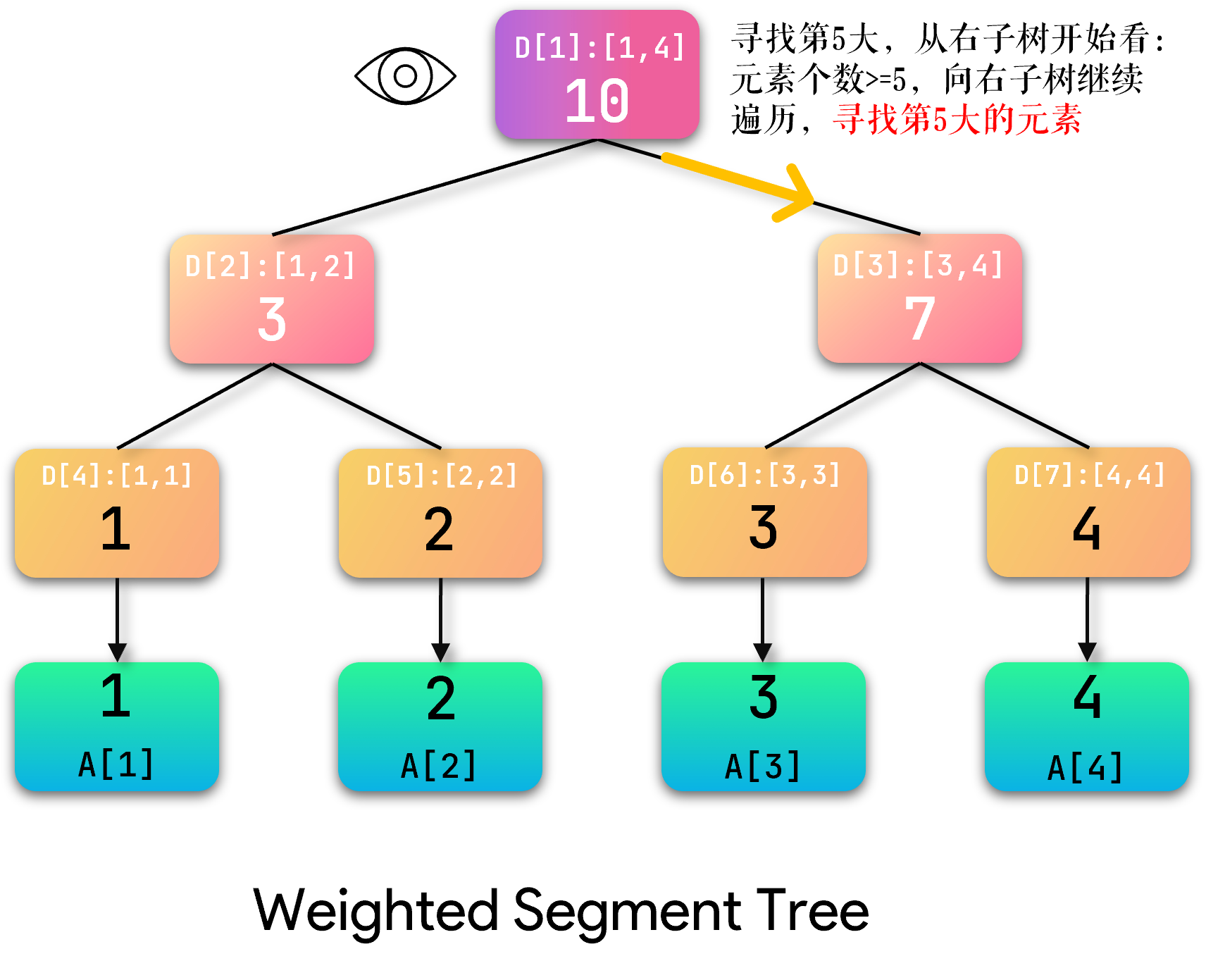

当前节点右子树包含 \(4\) 个元素，那么说明第 \(K\) 大不在右子树里，往左子树找，并且要减去右子树的 \(4\) 个元素，等效于在左子树中找第 \(1\) 大的元素。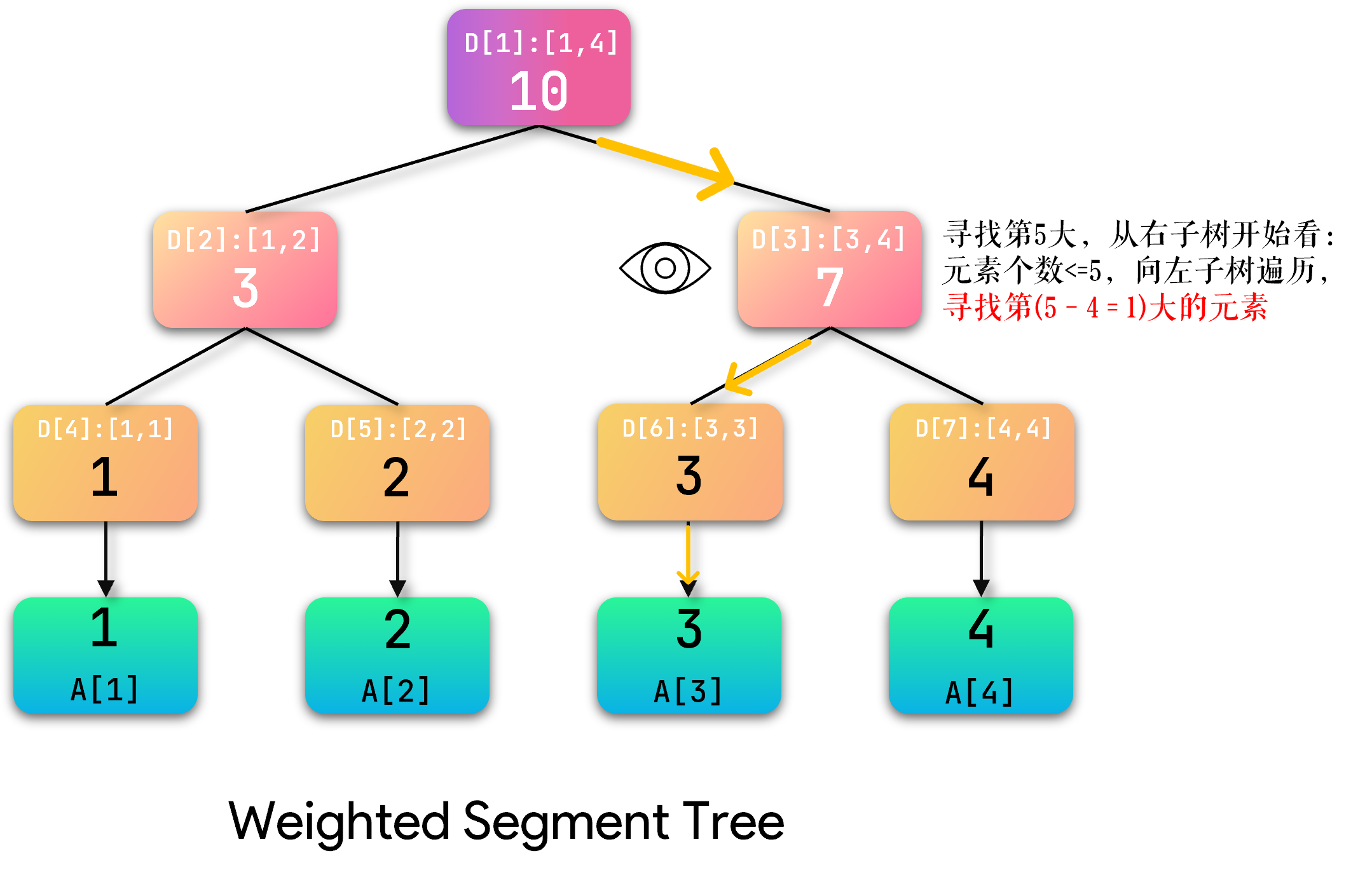

第 \(K\) 小与之类似，就是反过来了而已。

梳理一下：对于整列数中第 \(K\) 大/小的值，我们从根节点开始判断（这里按第 \(K\) 大为例），如果 \(K\) 比右儿子大，就说明第 \(K\) 大的数在左子树中。然后， \(K\) 要减去右子节点的值。（这是因为继续递归下去的时候，正确答案，整个区间的第 \(K\) 大已经不再是左子树表示区间的第 \(K\) 大了)。如此递归到叶子节点时即为答案。

code：

int query_kth(int p, int l, int r, int k){
    if(l == r) return l;
    int mid = (l + r) >> 1, right = tree[tree[p].rc ].sum;
    if(k <= right) return query(tree[p].rc , mid + 1, r, k);
    else return query(tree[p].lc, l, mid, k - right);
}

②单点更新（包含在动态开点中）

void Insert(int p,int l,int r,int k)
{
	if(!p) p = ++tot;
	if(l == r) { tree[p].sum++; return; }
	int mid = (l+r) >> 1;
	if(k<=mid) 
	{
		if(!tree[p].lc) tree[p].lc = ++tot;
		Insert(tree[p].lc,l,mid,k);
	}
	else 
	{
		if(!tree[p].rc) tree[p].rc = ++tot;
		Insert(tree[p].rc,mid+1,r,k);
	} 
	tree[p].sum = tree[tree[p].lc].sum + tree[tree[p].rc].sum;
}

③.查询某个数出现的个数

树上二分查找的思想：

int find(int p,int l, int r, int k)
{
    if (l == r) return tree[p].sum;
    else
    {
       	int mid = (l + r) >> 1;
        if (k <= mid) return find(tree[p].lc,l, mid , k);
        else return find(tree[p].rc,mid + 1, r, k);
    }
}

④查询一段区间内的数的个数

int Query(int p,int l,int r,int nl,int nr)
{
	if(!p) return 0;
	if(l>=nl && r<=nr) return tree[p].sum;
	int mid = (l+r) >> 1 , res = 0;
	if(nl<=mid) res += Query(tree[p].lc,l,mid,nl,nr);
	if(nr >mid) res += Query(tree[p].rc,mid+1,r,nl,nr);
	return res;
}

权值线段树的基本操作就这些，题目的话可以看洛谷题单里的题来做。