网络流
前前言:
本文内容 \(95\%\) 来自学长 surge_of_force 的讲课课件。
前言:
关于网络流有个生动的比喻,想象一个自来水厂向各处供水,自来水厂有无限多的水,但每条管子单位时间内允许的最大流量有限,现在钦定一个出水口为汇点,现在要做的就是在满足每一条管子不爆的情况下,最大化汇点流出的水量。
一、几个定义
1.网络
对于有向图 \(G = (V,E)\),其中每条边 \((u,v)\) 都有权值 \(W(u,v)\) ,称之为容量,图中
有两个特殊的点 \(s,t(s \not= t)\),称 \(s\) 为源点,\(t\) 为汇点,这个图称为网络。
2.流
对于任意的 \((u,v) \in E\) , 称 \(f(u,v)\) 为 \((u,v)\) 边的流量,\(f(u,v)\) 恒满足:
(1) \(f(u,v) \leq w(u,v)\) ,即一条边的流量不能超过其容量。
(2) \(f(u,v) = -f(v,u)\) ,即一条边的流量与其反向边的流量互为相反数。
(3) \(\forall x \in E - \{s,t\}\) , \(\Sigma_{(u,x) \in E} f(u,x) = \Sigma_{(x,v) \in E} f(x,v)\),即流入一个点的流量等于流
出这个点的流量。
3.残量网络
对于所有的 \(w(u,v) - f(u,v) > 0\) 的边组成的网络,称其为残量网络,残量网络中的边
可能不属于 \(E\)。
4.增广路
在原图 \(G\) 或其某一个残量网络中,一条每条边的剩余容量都大于 \(0\) 的从 \(s\) 到 \(t\) 的路
径,称为一条增广路。
二、最大流
给定网络 \(G=(V,E)\) 和源汇,求最多能从源点流出多少流量到汇点。
一个比较容易想到的思路是,不断地在残量网络中找寻增广路,直到没有增广路,此时
的总流量即为最大流,但这个做法有点问题,例如下面这张图:
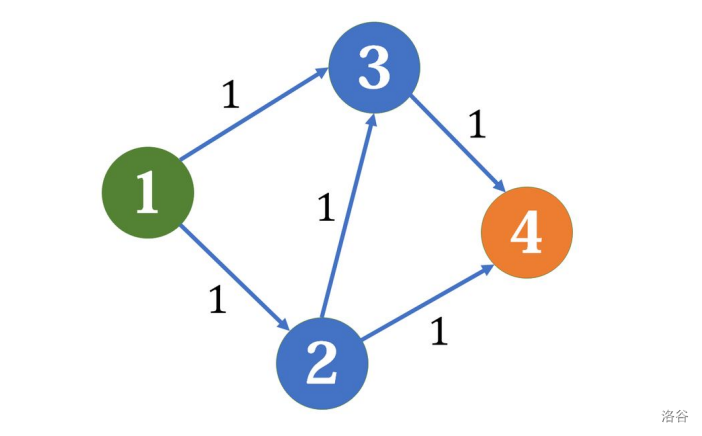
我们假设第一次增广,找到了 \(1\to2\to3\to4\) 这条边,于是残量网络变成了这样:
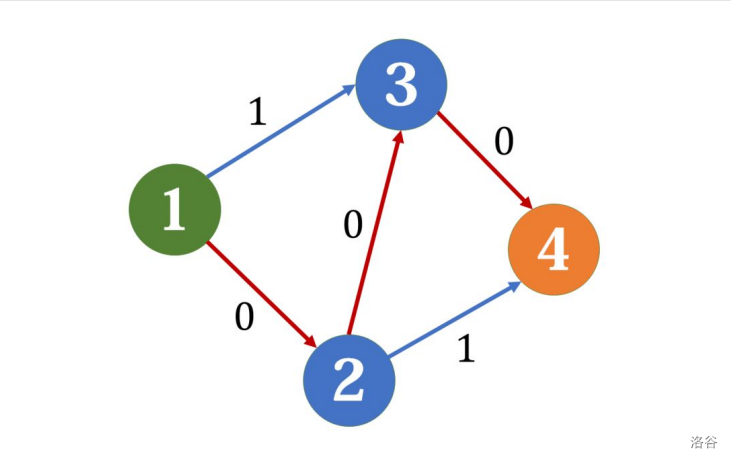
这里做了个近似,我们直接把边的流量改为其残余容量。
此时已经无法继续增广了,算法结束,但不难发现,其实走 \(1\to3\to4\) 和 \(1\to2\to4\) 总流量为 \(2\) ,这更优。
那怎么办?
我们考虑给程序一个反悔的机会,也就是说,建立一种方法,使得已经流过了某条边的流量再流回去,也就是建立反向边,为了保持总容量不变,反向边初始容量为 \(0\)。
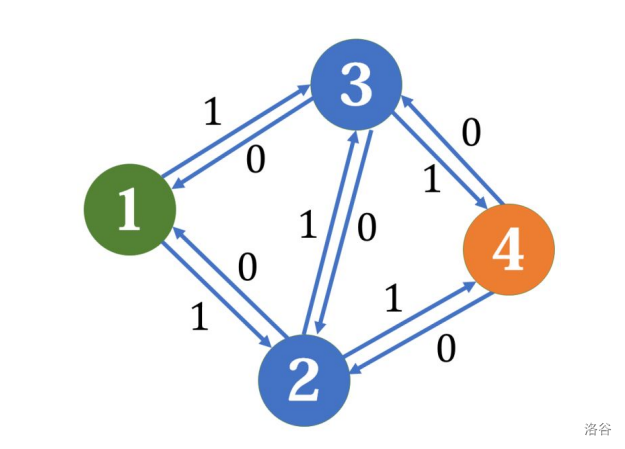
那么这是如果再走 \(1\to2\to3\to4\),残量网络就变成了这样:
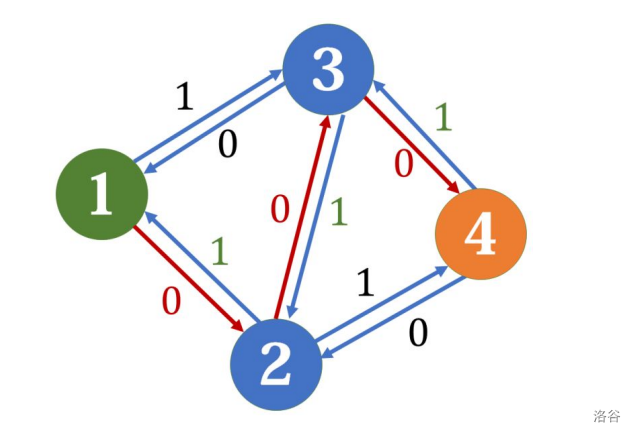
依然是为了保持总容量不变,在扣除正向边容量的同时,要给反向边加上相等的容量。
这时还可以继续增广:走 \(1\to3\to2\to4\) ,惊奇的发现,\(2\) 给 \(3\) 的流量又让 \(3\) 给退回去了!而此时相当于选择了两条路径: \(1\to3\to4\) 和 \(1\to2\to4\) ,总流量为 \(2\),得到了正确的结果。
算法一: Edmonds-Karp(EK)算法
EK算法通过 bfs 遍历原图或者是残量网络,每次查询一个增广路,如果增广路没有了,就停止。
复杂度上界是 \(O(nm^2)\) ,具体证明可以参照 OI Wiki。但是网络流一般是跑不满的,所以它能过模板题。
code:
#include<bits/stdc++.h>
#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 3e5 + 5;
const int M = 3e5 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int n,m,be,en;
int u,v,w;
int ans,pre[N],flow[N];
struct node{
int u,v,w,next;
}edge[M<<1]; int head[N],num_edge=1;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il void add(int from,int to,int dis)
{
edge[++num_edge] = (node){from,to,dis,head[from]};
head[from] = num_edge;
}
il int bfs()
{
queue <int> q;
memset(pre , 0 , sizeof pre);
q.push(be);
flow[be] = 1e9;
while(!q.empty())
{
int u = q.front(); q.pop();
if(u == en) break;
for(re int i=head[u];i;i=edge[i].next)
{
int v = edge[i].v , w = edge[i].w;
if(w && !pre[v])
{
pre[v] = i;
flow[v] = min(flow[u],w);
q.push(v);
}
}
}
return pre[en];
}
il int EK()
{
while(bfs())
{
ans += flow[en];
for(re int i=en;i!=be;i=edge[pre[i]^1].v)
{
edge[pre[i]].w -= flow[en];
edge[pre[i]^1].w += flow[en];
}
}
return ans;
}
signed main()
{
n = read() , m = read() , be = read() , en = read();
for(re int i=1;i<=m;i++)
{
u = read() , v = read() , w = read();
add(u,v,w) , add(v,u,0);
}
cout << EK();
return 0;
}
算法二:Dinic算法
最常用的网络流算法是 Dinic 算法。作为 FF/EK 算法的优化,它选择了先用 BFS 分层,再用 DFS 寻找。它的时间复杂度上界是 \(O(n^2m)\) 由于点数恒小于边数,所以更优 。所谓分层,其实就是预处理出源点到每个点的距离(注意每次循环都要预处理一次,因为有些边可能容量变为 \(0\) 不能再
走)。我们只往层数高的方向增广,可以保证不走
回头路也不绕圈子。
我们可以使用多路增广节省很多花在重复路线上的时间:在某点DFS找到一条增广路后,如果还剩下多余的流量未用,继续在该点DFS尝试找到更多增广路。
此外还有当前弧优化。因为在Dinic算法中,在一次DFS 中一条边增广一次后就不会再次增广了,所
以下次遍历到这个点的时候不需要再考虑已经使用过的边了。我们把head数组复制一份,就能表达现在增广到哪个边了。
code:
#include<bits/stdc++.h>
#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 2e2 + 5;
const int M = 5e3 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int n,m,be,en,ans;
int u,v,w;
int pre[N],flow[N],cur[N],dep[N];
struct node{
int u,v,w,next;
}edge[M<<1]; int head[N],num_edge=1;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il void add(int from,int to,int dis)
{
edge[++num_edge] = (node){from,to,dis,head[from]};
head[from] = num_edge;
}
il bool bfs()
{
queue <int> q;
q.push(be);
memset(dep , 0 , sizeof dep);
dep[be] = 1;
while(!q.empty())
{
int u = q.front(); q.pop();
for(re int i=head[u];i;i=edge[i].next)
{
int v = edge[i].v , w = edge[i].w;
if(!dep[v] && w)
{
dep[v] = dep[u] + 1;
q.push(v);
if(v == en) return 1;
}
}
}
return 0;
}
il int dfs(int u,int maxf)
{
if(u == en) return maxf;
int sum = 0;
for(re int i=cur[u];i;i=edge[i].next)
{
cur[u] = i;
int v = edge[i].v , &w = edge[i].w;
if(dep[v] == dep[u] + 1 && w)
{
int f = dfs(v,min(maxf,w));
sum += f , maxf -= f;
w -= f , edge[i^1].w += f;
if(maxf == 0) break;
}
}
if(!sum) dep[u] = 0;
return sum;
}
il int dinic()
{
while(bfs())
{
memcpy(cur , head , sizeof head);
ans += dfs(be,1e9);
}
return ans;
}
signed main()
{
n = read() , m = read() , be = read() , en = read();
for(re int i=1;i<=m;i++)
{
u = read() , v = read() , w = read();
add(u,v,w) , add(v,u,0);
}
cout << dinic();
return 0;
}
三、最小割
给一些定义:
1.割:对于网络 \(G\),其割代表一种点的划分方式,这种划分方式需要满足将 \(G\) 恰好分
为两部分 \(S,T\) ,且 \(s \in S\) ,\(t \in T\) 。
2.割的容量:表示所有的从 \(S\) 到 \(T\) 的边的容量之和,即 \(w(S,T) = \Sigma_{u\in S,v \in T}w(u,v)\)。
3.最小割:容量最小的割即为最小割。
如何求最小割?
这里有一条定理,极其简洁的解决了这个问题:
最大流 \(=\) 最小割。
证明如下:
可以把最小割认为是将一些边割断,使得整个图分为 \(S\),\(T\) 两部分,那么容易得到图中
所有的流量必定流经这些边中的某一条(否则无法从 \(s\) 到达 \(t\)),所以这些边的总流量 \(=\) 图的总流量
而 边的流量 \(\leq\) 边的容量,
所以这些边的总流量 \(\leq\) 这些边的总容量,
所以 图的总流量 \(\leq\) 这些边的总容量 ,
所以 流 \(\leq\) 割,
所以最大流 \(=\) 最小割。
那么求最小割实际上就是求最大流,这里不再赘述。
四:费用流
我们把前言里改一下,现在自来水厂想赚钱,于是每一单位的水流经某一条管时需要收
取一定费用 \(c(u,v)\),于是为了惠民,自来水厂想找到一种方法,使得流最大的同时费用最
小,这就是最小费用最大流。
回想一下前面的 EK 算法,我们找增广路时是随机找的,现在我不随机找了,我给每个点一个花费,我想要每次都在残量网络中找到花费最小的,咋办?
最短路。
有负权咋办?
spfa。
但它不是死了吗?
怎么会有出题人在负权图上卡spfa
#include<bits/stdc++.h>
#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 5e3 + 5;
const int M = 5e4 + 5;
const int INF = 1e9 + 7;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
struct node{
int u,v,w,c,next;
}edge[M<<1]; int head[N],num_edge=1;
int n,m,u,v,w,c,be,en;
int pre[N],flow[N],vis[N],dis[N];
int maxflow,mincost;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il void add(int from,int to,int dis,int c)
{
edge[++num_edge] = (node){from,to,dis,c,head[from]};
head[from] = num_edge;
}
il bool spfa()
{
queue <int> q;
memset(dis , 0x3f3f3f3f , sizeof dis);
memset(vis , 0 , sizeof vis);
memset(pre , 0 , sizeof pre);
memset(flow , 0 , sizeof flow);
vis[be] = 1 , flow[be] = INF , dis[be] = 0;
q.push(be);
while(!q.empty())
{
int x = q.front(); q.pop();
vis[x] = 0;
for(re int i=head[x];i;i=edge[i].next)
{
int y = edge[i].v , w = edge[i].w , c = edge[i].c;
if(dis[y] > dis[x] + c && w)
{
pre[y] = i;
dis[y] = dis[x] + c;
flow[y] = min(flow[x],w);
if(!vis[y]) { q.push(y); vis[y]=1; }
}
}
}
return flow[en];
}
il void EK()
{
while(spfa())
{
maxflow += flow[en];
mincost += flow[en] * dis[en];
for(re int i=en;i!=be;i=edge[pre[i]].u)
{
edge[pre[i]].w -= flow[en];
edge[pre[i]^1].w += flow[en];
}
}
cout << maxflow << " " << mincost;
}
signed main()
{
n = read() , m = read() , be = read() , en = read();
for(re int i=1;i<=m;i++)
{
u = read() , v = read() , w = read() , c = read();
add(u,v,w,c) , add(v,u,0,-c);
}
EK();
return 0;
}
五、上下界网络流
咕咕
六、例题
网络流24题


