Tarjan算法
Tarjan算法与无向图连通性
一、割点和桥的定义
给定一个无向连通图 $ G = (V,E) $
若对于 \(x \in V\) , 如果从图中删去节点 \(x\) 以及与 \(x\) 相连的边后,$ G $ 分裂成两个或者多个不相连的连通块,那么就说这个点是一个割点;
若对于 \(e \in E\) , 如果从图中删去这条边后,$ G $ 分裂成两个不相连的连通块,那么就说这个点是一个割边;
二、时间戳
我们一般用 \(dfn[x]\) 表示一个节点的时间戳。时间戳的定义是在 \(dfs\) 的过程中,每个节点第一次被访问的时间顺序。
三、追溯值
我们一般用 \(low[x]\) 表示一个节点的追溯值。追溯值的定义是一个节点通过非树边能够回到的最早节点的编号,也就是 \(dfn\) 的最小值。
它可以通过两种方式更新
-
若在搜索树上 \(x\) 是 \(y\) 的父节点,那么 \(low[x] = min(low[x],low[y])\)
-
若是非树边,那么 \(low[x] = min(low[x],dfn[y])\)
要注意的是,在无向图中,儿子到父亲的那条边不处理,要不然 \(low\) 值就都是 \(1\) 了,没有意义。
四、搜索树
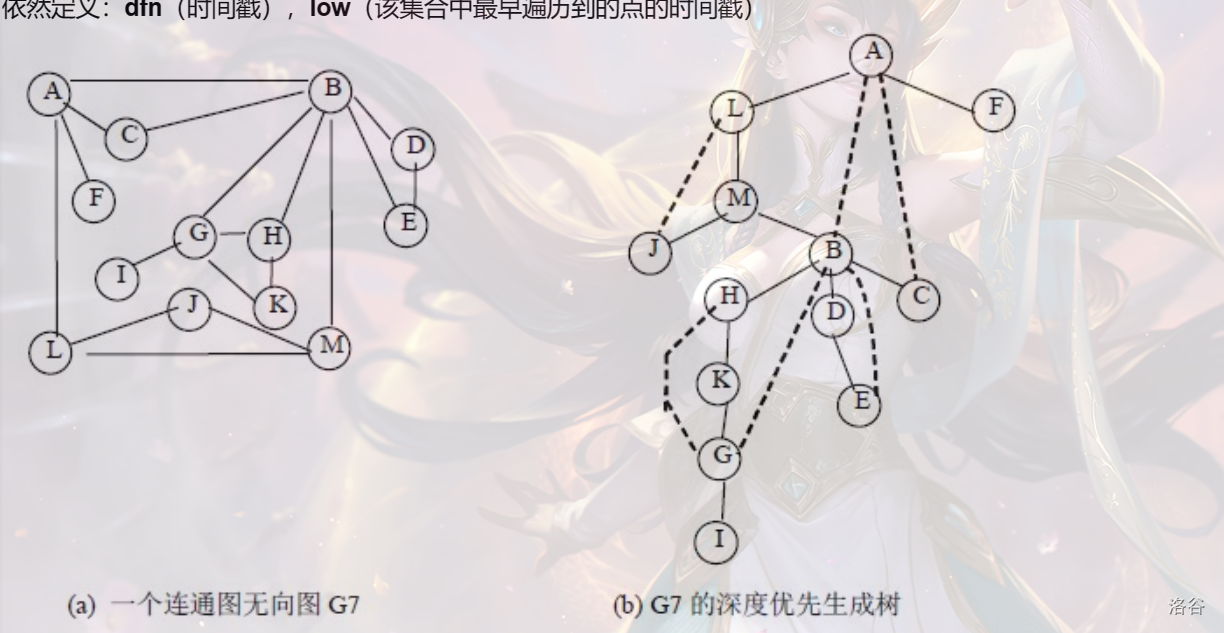
因为 \(tarjan\) 算法的过程究其根本是一个 \(dfs\) 的过程,所以在搜索的过程中会形成一棵搜索树
具体如图(摘自网上)
五、割边的判定
无向边 \((x,y)\) 是桥,当且仅当 \(low[y] > dfn[x]\)
具体如图
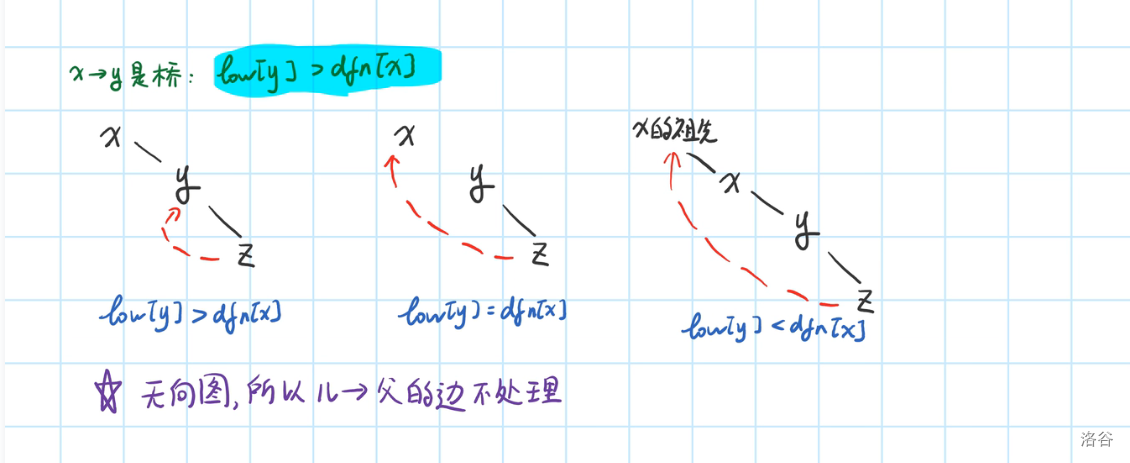
也就是说,\(y\) 回不到它父亲节点,所以它是桥。
同时,因为可能有重边存在,刚才提到的儿子->父亲的边不处理是仅针对两个点之间只有一条边的情况。如果有重边,那么显然可以更新。
为了解决这种情况,用到一个方法。我们把一条双向边的编号存储为 \(2\) 和 \(3\) , \(4\) 和 \(5\) 这样的,这样我们通过 i^1 的操作,便可以知道它这条边对应的反向边是哪个,我们不用这个更新便可。
code
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 2e4 + 5;
const int M = 1e5 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int n,m,u,v,cnt,tot,idx,ans;
int low[N],dfn[N],bridge[N];
struct node{
int u,v,next;
}edge[M<<1]; int head[N],num_edge;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il void add(int from,int to)
{
edge[++num_edge] = (node){from,to,head[from]};
head[from] = num_edge;
}
il void tarjan(int x,int in_edge)
{
dfn[x] = low[x] = ++tot;
for(re int i=head[x];i;i=edge[i].next)
{
int y = edge[i].v;
if(!dfn[y])
{
tarjan(y,i);
low[x] = min(low[x],low[y]);
if(low[y] > dfn[x]) bridge[i] = bridge[i^1] = 1;
}
else if(i != (in_edge^1)) low[x] = min(low[x],dfn[y]);
}
}
signed main()
{
n = read() , m = read();
num_edge = 1;
for(re int i=1;i<=m;i++)
{
u = read() , v = read();
add(u,v) , add(v,u);
}
for(re int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
for(re int i=2;i<num_edge;i+=2)
if(bridge[i]) cout << edge[i].u << " " << edge[i].v << "\n";
return 0;
}
六、割点的判定
点 \(x\) 是桥,当且仅当 \(low[y] \geq dfn[x]\)
具体还是如图
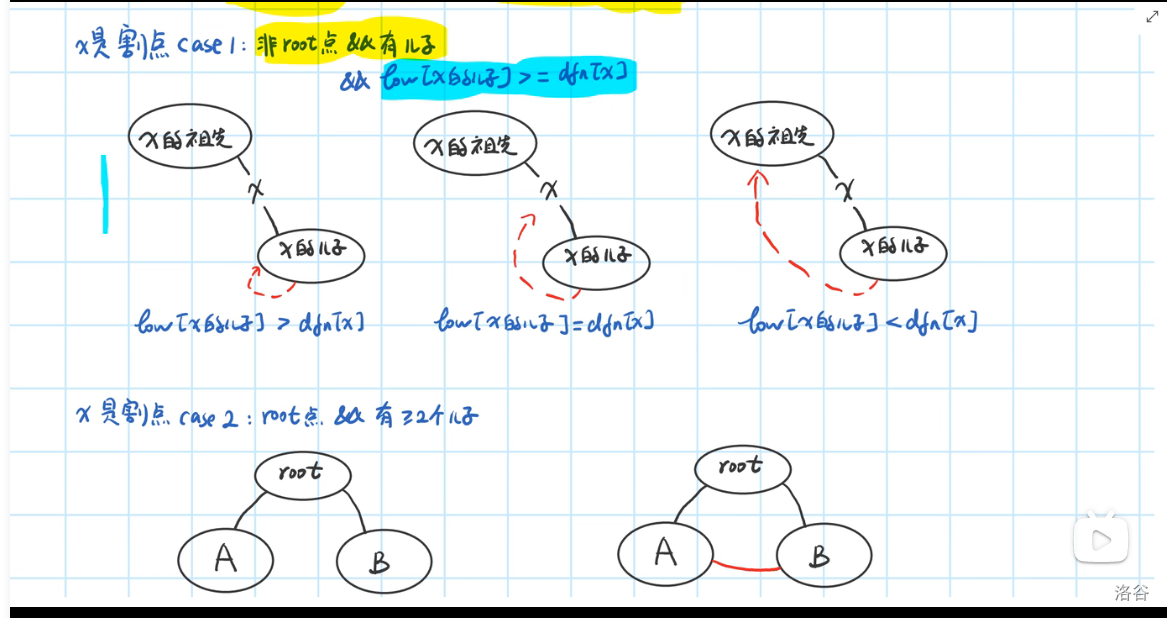
这个点回不到他父亲节点的上边,也就是说被隔离开来了,即使回到他的父亲节点也没用,所以说是大于等于。
这个没啥需要注意的点。
code
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 2e4 + 5;
const int M = 1e5 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int n,m,u,v,cnt,tot,idx,ans;
int low[N],dfn[N],cut[N];
struct node{
int u,v,next;
}edge[M<<1]; int head[N],num_edge;
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il void add(int from,int to)
{
edge[++num_edge] = (node){from,to,head[from]};
head[from] = num_edge;
}
il void tarjan(int x,int fa)
{
dfn[x] = low[x] = ++tot;
int child = 0;
for(re int i=head[x];i;i=edge[i].next)
{
int y = edge[i].v;
if(!dfn[y])
{
tarjan(y,fa);
low[x] = min(low[x],low[y]);
if(low[y] >= dfn[x] && x != fa) cut[x] = 1;
if(x == fa) child++;
}
low[x] = min(low[x],dfn[y]);
}
if(x == fa && child >= 2) cut[x] = 1;
}
signed main()
{
n = read() , m = read();
for(re int i=1;i<=m;i++)
{
u = read() , v = read();
add(u,v) , add(v,u);
}
for(re int i=1;i<=n;i++) if(!dfn[i]) tarjan(i,i);
for(re int i=1;i<=n;i++) if(cut[i]) ans++;
cout << ans << "\n";
for(re int i=1;i<=n;i++) if(cut[i]) cout << i << " ";
return 0;
}
无向图的双连通分量
咕咕咕
Tarjan算法与有向图连通性
强连通分量
定义:
一张图里,如果有一些点两两之间能直接或间接到达,那么这些点就叫一个强连通分量(说白了就是环)
边的种类
树边:一张图中可以构成树的边
回边:回到祖先的边 —> 可以形成强连通分量
横叉边:不连到祖先的边 —>可以扩大强连通分量
应用算法:tarjan
\(dfn\) : 第 \(i\) 个点被 \(dfs\) 的顺序
\(low\):从 \(i\) 出发走三种边中 \(dfn\) 最小是多少
如何判断强连通分量:如果扫完 \(dfn\) 和 \(low\) 值相等,那么说明它是它所在的强连通分量中最上面的那个。
用栈处理,如果回到了一个 \(dfn\) 和 \(low\) 相等的时候,就把栈内大于他的弹出。
用处
\(1\).缩点 – > 拓扑 —> dp
$ 2.2-SAT $


