导数、积分瞎记

1|0定义式

$$f^{{}^{\prime }}(x)=\underset{\mathrm{\Delta }x\to 0}{lim}\frac{f(x+\mathrm{\Delta }x)-f(x)}{\mathrm{\Delta }x}$$

导数不是用来测量瞬时变化率的，而是测量瞬时变化率的最佳近似。$\mathrm{\Delta }x$ 再小也是存在的，它也是一段变化量。

2|0常见导数：

$$(a^x{)}^{{}^{\prime }}=x{a}^{x-1}$$

$$(C{)}^{{}^{\prime }}=0$$

$$(e^k{)}^{{}^{\prime }}=e^k$$

$$(\ln x{)}^{{}^{\prime }}=\frac{1}{x}$$

$$(\sin x{)}^{{}^{\prime }}=\cos x$$

$$(\cos x{)}^{{}^{\prime }}=-\sin x$$

3|0不常见的：

$$(\tan x{)}^{{}^{\prime }}=\frac{1}{{\cos }^{2}x}$$

$$(\cot x{)}^{{}^{\prime }}=-\frac{1}{{\sin }^{2}x}$$

$$a^x=\ln a(a^x)$$

$$({\log }_{a}x{)}^{{}^{\prime }}=\frac{1}{x\ln a}$$

4|0运算法则

$$(f(x)+g(x)+h(x)+\dots {)}^{{}^{\prime }}=f^{{}^{\prime }}(x)+g^{{}^{\prime }}(x)+h^{{}^{\prime }}(x)+\dots$$

$$(kf(x){)}^{{}^{\prime }}=k{f}^{{}^{\prime }}(x),k\text{是常数}$$

$$(f(x)\cdot g(x){)}^{{}^{\prime }}=f^{{}^{\prime }}(x)\cdot g(x)+f(x)\cdot g^{{}^{\prime }}(x)$$

$$(\frac{f(x)}{g(x)}{)}^{{}^{\prime }}=\frac{f^{{}^{\prime }}(x)\cdot g(x)-f(x)\cdot g^{{}^{\prime }}(x)}{g^2(x)}$$

$$(g(f(x){)}^{{}^{\prime }}=g^{{}^{\prime }}(f(x))\cdot f^{{}^{\prime }}(x)$$

这个就是复合函数的导数，举个例子。

$$(\sqrt{\sin x}{)}^{{}^{\prime }}=\frac{1}{2}{\sin }^{-\frac{1}{2}}x\cdot \cos x$$

遵循一个链式法则，把里面换个元，逐层分解即可。再来个例子

$$(\sqrt{\sin x^2})=\frac{1}{2}{\sin }^{-\frac{1}{2}}{x}^2\cdot \cos x^2\cdot 2x$$

$$={\sin }^{-\frac{1}{2}}{x}^2\cdot \cos x^2\cdot x$$

5|0导数和函数单调性

好神奇。
给个例子。

$$f(x)=x^2-2x+3$$

运用初中知识，易知 $x<1$ 时单调递减，$x>1$ 时单调递增。

我们考虑导数的几何意义：反映了函数图像上一个点的斜率。我们给 $f(x)$ 求个导看看：

$$f^{{}^{\prime }}(x)=2x-2$$

在 $x>1$ 时，$f^{{}^{\prime }}(x)>0$ ，这就代表着 $f(x)$ 在 $x>1$ 的时候是单调递增的；同样的，在 $x<1$ 时，$f^{{}^{\prime }}(x)<0$ ，这就代表着 $f(x)$ 在 $x<1$ 的时候是单调递减的；而当 $x=1$ 的时候 $f^{{}^{\prime }}(x)=0$ ，说明该处斜率为 $0$ ，是个拐点。

有了这个，我们就可以很快速的判断单调性和拐点等问题了/oh。

还有，当 $f^{{}^{\prime }}(x)>0$ 时，$f^{{}^{\prime }}(x)$ 越大，函数增得越快；同理，当 $f^{{}^{\prime }}(x)<0$ 时，$f^{{}^{\prime }}(x)$ 越小，函数降得越快。

6|0极值与最值

6|1极大值与极小值

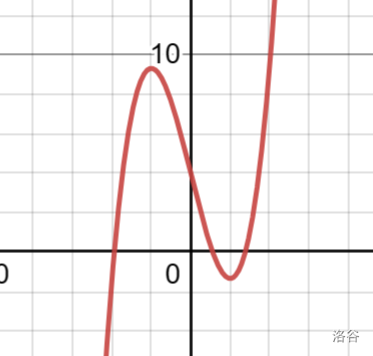
来个例子

$$f(x)=\frac{1}{3}{x}^3-4x+4$$

导一下

$$f^{{}^{\prime }}(x)=x^2-4=(x+2)(x-2)$$

这是 $f(x)$ 的图像

由导数我们可以知道，当 $x\in (-\mathrm{\infty },-2)$ 时，$f^{{}^{\prime }}(x)>0$，函数单调递增；当 $x\in [-2,2]$ 时，$f^{{}^{\prime }}(x)<0$，函数单调递减；当 $x\in (2,\mathrm{\infty })$ 时，$f^{{}^{\prime }}(x)>0$，函数又单调递增。

这里出现了两个极值点：$-2$ 和 $2$。

极值点就是导数为 $0$ 的点的横坐标。这些点就是所说的拐点，它左边和右边的单调性是相反的。

这里，$-2$ 是极大值点，$f(-2)$ 的值比它的邻域的值都要大；$2$ 是极小值点，$f(2)$ 的值比它的邻域的值都要小。

同时，$f(-2)$ 就被称为极大值，$f(2)$ 就被称为极小值。

6|2最值

$x\in [a,b]$ 的最值只会出现在两种地方：极值点和端点。因此求导一下，看看是最小值点还是最大值点，再按照题意操作一番就完事了。

7|0洛必达法则

什么都洛只会害了你。

内容

当 $x\to t$ 时，$f(x)$ 与 $g(x)$ 同时趋近于 $0$,
则

$$\underset{x\to t}{lim}\frac{f(x)}{g(x)}=\underset{x\to t}{lim}\frac{f^{{}^{\prime }}(x)}{g^{{}^{\prime }}(x)}$$

当 $x\to +\mathrm{\infty }$ 时，$f(x)$ 与 $g(x)$ 同时趋近于 $+\mathrm{\infty }$,
则

$$\underset{x\to \mathrm{\infty }}{lim}\frac{f(x)}{g(x)}=\underset{x\to \mathrm{\infty }}{lim}\frac{f^{{}^{\prime }}(x)}{g^{{}^{\prime }}(x)}$$

给道例题感觉一下。

对任意 $x>0$ ，有 $(x+1)\ln (x+1)>ax$ 恒成立，则 $a$ 的范围是_____

很自然的给它分个参

$$a<\frac{(x+1)\ln (x+1)}{x}$$

设

$$f(x)=\frac{(x+1)\ln (x+1)}{x}$$

,那么我们只需要求这个函数的最小值即可。

最小值怎么求？导一下。最小值怎么求？导一下。

$$f^{{}^{\prime }}(x)=\frac{x-\ln (x+1)}{x^2}$$

这玩意也很难看单调性啊，怎么办？导一下。怎么办？导一下。

令 $h(x)=x-\ln (x+1)$

则 $h^{{}^{\prime }}(x)=1-\frac{1}{x+1}$

当 $x>0$ 时，$h^{{}^{\prime }}(x)$ 恒 $>0$，所以 $h(x)$ 在 $x>0$ 上是单调递增的，当 $x=0$ 时，$h(x)=0$，这就说明了 $f^{{}^{\prime }}(x)$ 在 $x>0$ 的时候也是恒 $>0$ 的，这就又说明 $f(x)$ 在 $x>0$ 范围内单调递增。那么最小值就在 $x=0$ 的时候取得。

因此 $a\le f(0)$ 即可，但是 $f(0)$ 的时候这个式子是无解的啊，怎么办？洛一下。怎么办？洛一下。

设 $m=f(0)$ ，则有

$$m=\underset{x\to 0}{lim}\frac{(x+1)\ln (x+1)}{x}$$

当 $x=0$ 时，

$$\frac{(x+1)\ln (x+1)}{x}=\frac{0}{0}$$

，说明上下都是趋于 $0$ 的。

应用洛必达法则，得：

$$m=\underset{x\to 0}{lim}\frac{(x+1)\ln (x+1)}{x}$$

$$=\underset{x\to 0}{lim}\frac{[(x+1)\ln (x+1){]}^{{}^{\prime }}}{x^{{}^{\prime }}}$$

$$=\frac{\ln (x+1)+1}{1}$$

这时候 $x=0$ 就是有意义的了，答案就是 $1$，所以 $a\le 1$。

高考大题好像不让用，但是选择填空可以用/cy。但是不知道这玩意在 OI 中有没有用，觉得好玩，故记之。

8|0帕德逼近

这又是什么黑科技，记一波。

$$e^x\approx \frac{x^2+6x+12}{x^2-6x+12},x\in (-2,2)$$

$$\ln (x+1)\approx \frac{3x^2+6x}{x^2+6x+6},x\in (-1,2)$$

往后面差值就比较大了。

9|0麦克劳林公式

本质是泰勒公式在 $x=0$ 的一种特殊情况。

$$P(x)=f(0)+\frac{df}{dx}(0)\frac{x}{1!}+\frac{d^{2}f}{d{x}^2}(0)\frac{x^2}{2!}+\frac{d^{3}f}{d{x}^3}(0)\frac{x^3}{3!}+\dots$$

本质上就是高阶导数和多项式的一一对应，求一个最近似的多项式函数。

真正的泰勒公式

$$P(x)=f(a)+\frac{df}{dx}(a)\frac{(x-a{)}^1}{1!}+\frac{d^{2}f}{d{x}^2}(a)\frac{(x-a{)}^2}{2!}+\frac{d^{3}f}{d{x}^3}(a)\frac{(x-a{)}^3}{3!}+\dots$$

取 $f(x-a)$ 的目的就是做一个近似，应该就是发生了一个位移用 $f(x-a)$ 来近似。

黑科技。
当 $x\to 0$ 时，一般就是 $|x|\le 0.1$ ，则有

$$e^x\approx 1+x+\frac{x^2}{2!}+\frac{x^3}{3!}$$

这个就好理解了，美丽的 $e^x$ 几阶导都是它自己，因此当 $x\to 0$ 时，套入公式，十分美丽。

$$\ln (1+x)\approx x-\frac{x^2}{2}+\frac{x^3}{3}$$

$$\sqrt{1+x}\approx 1+\frac{x}{2}-\frac{x^2}{8}+\frac{x^3}{16}$$

$$\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}\dots$$

$$\cos x=1-\frac{x^2}{2}+\frac{x^4}{4!}\dots$$

级数：以 $\cos x$ 为例，如果我们让上式推广到无限项，这无限多项的和，就叫做级数(series)。

收敛和发散：如果一个级数加的越多，它的和越接近某个确定的数值的话，，我们就可以说这个级数收敛到那个值，也就是说这个级数就等于它收敛到的值；反之，如果加的越多，级数不接近任何值，就称这个级数时发散的。

收敛半径：把在用来近似那个点（比如在 $x=1$ 的时候用一个多项式近似 $\ln 1$）周围，能够让多项式收敛的最大取值范围，就叫做这个级数的收敛半径。

10|0拉格朗日定理

感觉是求导比斜率，把割线问题转化成切线，也就是导数问题。

两点之间的平均斜率就是两点之间的斜率。

具体可以看这个视频。
又一个黑科技。

11|0定积分

微分是割线的斜率，导数是切线的斜率，当$\mathrm{\Delta }x\to 0$ 时，它们就是相等的。

导数：是指函数在某一点处变化率的最佳近似。

微分：是指函数在某一点处（趋近于无穷小）的变化量，是一种变化的量

11|1定义

$f(x)$ 定义在 $[a,b]$ ，任分 $[a,b]$ 为小区间点，分点 $a=x_0<x_1<\cdots <x_n=b$ ，这称为 $[a,b]$ 的一个分割。

若 $\mathrm{\exists }I\in \mathbb{R}$ ，对 $[a,b]$ 的所有分割都有

$$\underset{\lambda \to 0}{lim}\sum _{i=1}^{n}f({\xi }_i)\mathrm{\Delta }{x}_i=I({\xi }_i\in [x_{i-1},x_i],\lambda \in max\{\mathrm{\Delta }{x}_i\})$$

则称 $f(x)$ 在 $[a,b]$ 可积。

$I$ 称为 $f(x)$ 在 $[a,b]$ 的定积分，记作

$$I={\int }_a^{b}f(x)dx$$

11|2可积的条件

两种情况都可

• （1）：连续必可积

• （2）：有界且存在有限个第一类间断点

12|0微积分基本定理

神。

$$g(x)={\int }_a^{x}f(t)dt,\text{且}{g}^{{}^{\prime }}=f$$

这个说明的是导数和积分其实是互逆的。

积分后再求导得到的是原函数。

求导后再积分得到的是全体原函数（有常数）。

$${\int }_a^{b}f(x)dx=F(b)-F(a)$$

下面这个就是牛顿-莱布尼茨公式。其中 $F(x)$ 表示的是 $f(x)$ 的原函数，$F(x)$ 的导数是 $f(x)$。

举个例子 $f(x)=x^2$ ，那么 $F(x)=\frac{1}{3}{x}^3+d$ ，但是 $F(b)-F(a)$ 后 常数项就消没了。

13|0自适应辛普森积分

花了两天学你的前置知识。

首先看 3b1b 的视频我们能得出一个小公式。

$\text{一段函数的平均高度}=\frac{\text{面积}}{\text{宽度}}$

其中的面积就用积分求。

13|1辛普森公式

用来解决二次函数的定积分。

对二次函数 $f(x)=a{x}^2+bx+c$ 在区间 $[l,r]$ 上求定积分，而一阶定积分的几何意义就是图像与 $x$ 轴围成的面积。

求 $f(x)$ 的原函数：

$$F(x)=\frac{a}{3}{x}^3+\frac{b}{2}{x}^2+cx+d$$

运用牛顿-莱布尼茨公式：

$${\int }_l^{r}f(x)dx=\frac{a}{3}(r^3-l^3)\frac{b}{2}(r^2-l^2)+c(r-l)$$

$$=(r-l)[\frac{a}{3}(r^2+l^2+lr)+\frac{b}{2}(r+l)+c]$$

$$=\frac{(r-l)(2a{l}^2+2a{r}^2+2alr+3bl+3br+6c)}{6}$$

$$=\frac{r-l}{6}[(a{l}^2+bl+c)+(a{r}^2+br+c)+4(a(\frac{l+r}{2}{)}^2+b(\frac{l+r}{2})+c)]$$

$$=\frac{(r-l)(f(l)+f(r)+4f(\frac{l+r}{2}))}{6}$$

这就是区间宽度 $\times$ 平均高度。

14|0自适应辛普森积分法

它的原理是把可积函数分成很多段，每段就可以用二次函数来拟合，也就是把这一段用二次函数来拟合（感觉跟泰勒展开很相似，不过泰勒展开是多项式），套用辛普森公式进行近似计算。

不过这个误差可能会比较大，what should we do？二分。每次判断当前段和二次函数的相似程度，如果足够相似就直接代辛普森公式计算即可，否则将当前段分割成左右两段递归求解。

如何判断当前段和二次函数是否相似？把整段带入公式求一下积分，再将当前段分成左右两端分别代入公式求一下积分。如果当前段的积分和分割后两端的积分相差很小，就可以认为当前段和二次函数是相似的，不用递归分割了。

代码也很简单。

const double eps = ; 

double a,b,c,d,l,r;

il double f(double x) { ... }//题目中给出的函数

il double Simpson(double l,double r) { return (r-l)*(f(l)+f(r)+4*(f((l+r)/2)))/6; }//辛普森公式

il double Adaptive_Simpson(double l,double r,double ans)//分治思想
{
	double m = (l+r) / 2.0 , a = Simpson(l,m) , b = Simpson(m,r);
	if(fabs(a+b-ans) < eps) return ans;
	else return Adaptive_Simpson(l,m,a) + Adaptive_Simpson(m,r,b);
}

signed main()
{
	scanf("%lf%lf%lf%lf%lf%lf",&a,&b,&c,&d,&l,&r);
	printf("%.6lf",Adaptive_Simpson(l,r,Simpson(l,r)));
	return 0;
}

为了精确，我们要将 eps 设小一点，往往是 eps = 1e-10。

由此可以看出，这个算法的复杂度是 $O(\log \frac{n}{\text{eps}})$ ，其中 $n$ 代表的是积分的上限$-$下限，也就是 $r-l$。

__EOF__

本文作者：bloodstalk
本文链接：https://www.cnblogs.com/bloodstalk/p/17432773.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！