博弈论
博弈论在 OI 中主要研究组合博弈,可能也会与其它的知识点相结合。做博弈论题时,我们要利用已有的博弈结论,或是建出模型解决问题。
组合博弈
组合博弈一般分为两种:
-
平等博弈:可允许的操作只和当前局面的状态而和操作的玩家无关。
-
不平等博弈:可允许的操作还和当前操作的玩家相关。
比如说围棋,就是一个不平等博弈,因为黑白子与当前轮到哪名玩家有关。
OI 中一般研究和平等博弈(不平等博弈我不会/cy)相近的公平组合游戏。
公平组合游戏 ICG
若一个游戏满足
-
- 有两名玩家交替行动;
-
- 在游戏进程的任意时刻,可以执行的合法行动与轮到哪名玩家无关;
-
3.不能行动的玩家判负。
则称该游戏为一个 公平组合游戏。
一些定义
有向图游戏(博弈图)
给定一个有向无环图,图中有一个唯一的起点,在起点上放有一枚棋子。两名玩家交替地把这枚棋子沿着有向边进行移动,每次可以移动一步,无法移动者判负。该游戏被称为 有向图游戏。
事实上,任何一个公平组合游戏都可以转化为有向图游戏。具体方法是,把每个局面(游戏过程中面临的状态)看成图中的一个节点,并且从每个局面向沿着合法行动能够到达的下一个局面连有向边。
组合游戏向图的转化,实际上就是实现了建立了博弈论的数学模型。
必胜态和必败态
必胜态:存在一种策略,可以让剩余的状态变成必败态留给对手的局面。
必败态:不管采取什么策略,这一步行动后对手都处于必胜态的局面。
简化一下,就是三个定理,这也是博弈论的核心:
-
没有后继状态的状态是必败态。
-
可以移动到必败态的是必胜态。
-
只能移动到必胜态的是必败态。
如果博弈图是一个 DAG ,我们通过这三个定理就能用 \(O(N+M)\) 的时间(\(N\) 为状态总数,\(M\) 为边数)得出每个状态是必胜态还是必败态。
有向图的核
给定一张 DAG 图 \(G=(V,E)\) ,如果 \(V\) 的一个子集 \(S\) 满足:
-
\(S\) 是独立集。
-
\(\complement_VS\) 中的点都可以一步到达集合 \(S\) 中的点。
则称 \(S\) 是图 \(G\) 的一个 核。
结论:核内节点对应组合游戏的 必败态。
\(S\) 内的节点没有出度,必败。
几个经典的组合游戏
nim 博弈
给定 \(n\) 堆物品,第 \(i\) 堆物品有 \(a_i\) 个。两名玩家轮流行动,每次可以任选一堆,取走任意多个物品,可把一堆取光,但不能不取。取走最后一件物品者获胜。两人都采用最优策略,问先手能否必胜。
我们整局游戏第一个行动的称为先手,第二个行动的称为后手。若在某一局面下无论采取何种行动,都会输掉游戏,则称该局面必败。
所谓采取最优策略是指,若在某一局面下存在某种行动,使得行动后对手面临必败局面,则优先采取该行动。同时,这样的局面被称为必胜。我们讨论的博弈问题一般都只考虑理想情况,即两人均无失误,都采取最优策略行动时游戏的结果。
nim 博弈不存在平局,只有先手必胜和先手必败两种情况。
结论:若 \(a_1\ \hat{} \ a_2\ \hat{} \ \dots\ \hat{} \ a_n \not=0\),则先手必胜;反之,先手必败。
按照定义,证明分两部分:
- 必胜态的后继状态至少存在一个必败态。
证明:设\(a_1\ \hat{} \ a_2\ \hat{} \ \dots\ \hat{} \ a_n =s\not=0\) ,设 \(s\) 的二进制为 \(1\) 的最高位是第 \(k\) 位,那么 \(a_1\dots a_n\) 一定有奇数个 \(a_i\) 的二进制的第 \(k\) 位为 \(1\)。
用 \(a_i \ \hat{} \ s\) 去替换 \(a_i\) ,可得$
a_1\ \hat{} \ \dots \ \hat{} \ a_i\ \hat{} \ s\ \hat{} \ \dots \ \hat{} \ a_n $
\(= s \ \hat{} \ s=0\) ,\(0\) 是必败态。
又因为 \(a_i\ \hat{} \ s <a_i\) ,所以替换合法。
- 必败态的后继状态均为必胜态
证明:设\(a_1\ \hat{} \ a_2\ \hat{} \ \dots\ \hat{} \ a_n =0\) ,那么相同位上 \(1\) 的个数就是偶数,此时无论减少那个数,都会使得异或和 \(\not= 0\)。
代码也比较简单
il void Main()
{
n = read() , flag = 1;
x = read();
for(re int i=2;i<=n;i++) x ^= read();
if(!x) puts("No"); else puts("Yes");
}
Bash 博弈
总共有 \(n\) 个石子,每次每人可以取 \(1\thicksim k\) 个石子,问先手必胜状态。
结论:它的必败态为 $n\equiv 0(\text{mod} \ k+1) $
证明:随便画画图就能知道 \(1\thicksim k\) 可以转移到 \(0\) ,所以它们是必胜态;而 \(k+1\) 只能转移到 \(1\thicksim k\) ,都是必胜态,所以它是必败态,如此反复,可得结论。
Wythoff 博弈
有两堆石子,石子数可以不同。两人轮流取石子,每次可以在一堆中取,或者从两堆中取走相同个数的石子,数量不限,取走最后一个石头的人获胜。判定先手是否必胜。
结论:假设两堆石子为 \((a,b)\)(其中 \(a<b\)),那么先手必败,当且仅当 \((b-a) \times \frac{\sqrt 5 +1}{2} = a\)
\(\frac{\sqrt 5+1}{2}\) 其实就是黄金分割。博弈论这东西真奇妙。
证明:有点奇妙,我选择记结论(
Fibonacci 博弈
一堆个数为 \(n\) 的石子,有两条规则:
1. 先手不能在第一次把所有的石子取完,至少取 \(1\) 颗
2.之后每次可以取的石子数至少为 \(1\) ,至多为对手刚取的石子数的 \(2\) 倍。
约定取走最后一个石子的人是赢家,求必胜态。
结论:后手必胜,当且仅当石子数为斐波那契数。
证明:
设 \(f_k\) 表示斐波那契第 \(k\) 项,规定 \(f_1 = f_2 =1\)(\(f_1 = 0 ,f_1 = 1\)也没影响)。
首先观察斐波那契数列,我们能得到三条性质,自己推推就能推出来:
必要性:
数学归纳法:
-
当 \(k=3\) 时,\(n = f_3 =2\) ,先手只能取一个,显然后手必胜
-
\(k>3\) 时,假设 \(n=a_i(3\leq i < k)\) 时后手必胜,则只需证明 \(n=a_k\) 时结论成立即可。\(n=f_k = f_{k-1} + f_{k-2}\) 分成 \(f_{k-1}\) 和 \(f_{k-2}\) 这两堆。设先手取 \(x\) 颗,后手取 \(y\) 颗,分三种情况讨论。
1.若 \(x \ge f_{k-2}\) ,剩下的石子数 \(\leq f_{k-1} < 2f_{k-2}\) ,后手可以直接取完。
-
若 \(\frac{1}{3}f_{k-2} \leq x < f_{k-2}\) ,则 \(f_{k-2}\) 这一堆里剩下的石子数 \(< \frac{2}{3}f_{k-2}\) ,后手可以直接取完,那就只剩下 \(f_{k-1}\) 那一堆了 ,由假设知,后手在 \(f_{k-1}\) 这一堆必胜。
-
若 \(x < \frac{1}{3}f_{k-2}\) ,则后手无法取完 \(f_{k-2}\) ,但是我开挂了( ,由假设知,后手在 \(f_{k-2}\) 这一堆必胜,那就到了 \(2\) 的情况,\(2\) 的情况也是必胜,所以它必胜。
充分性
首先有一个 Zeckendorf 定理:任何正整数可以表示为若干个若干个不连续的斐波那契数之和。
把 \(n\) 分解 ,\(n = f_{p_1} + \dots + f_{p_k}(p_1 < p_2 < \dots < p_k)\)
先手存在一种必胜策略:先把 \(f_{p_1}\) 取完,又因为 \(p_2 - p_1 \geq 2\) ,则有 \(f_{p_2} > 2f_{p_1}\) ,所以后手取不完 \(f_{p_2}\) ,这就相当于证明充分性的情况了,只不过先手在这一堆里变成了后手,后手在这一堆里变成了先手。
SG 函数
前置知识:mex 运算
\(\text{mex}(S)\) 表示不属于集合 \(S\) 中的最小非负整数。
例如 \(\text{mex}(\{0,1,2\}) = 3,\text{mex}(\{1,2\}) = 0\)
SG 函数
SG 函数是对博弈图中每一个节点的评估函数。
在有向图游戏中,规定图 \(G\) 的 \(SG\) 函数值为有向图游戏起点 \(s\) 的 \(SG\) 函数值,即 \(SG(G) = SG(s)\) ,并规定终点的 \(SG\) 函数值为 \(0\)。
\(SG\) 函数的求法如下:
在有向图游戏中,对于每个节点 \(x\) ,设从 \(x\) 出发共有 \(k\) 条有向边,分别到达节点 \(y_1,y_2,\dots,y_k\) ,那么定义 \(x\) 的 \(SG\) 函数值为它的后继节点的 \(SG\) 函数值构成的集合再执行 \(\text{mex}\) 运算的结果,即:
引用董晓老师的一个例子
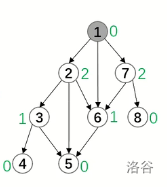
我们可以发现若 \(SG(x) =0\) ,这是个必败态;若 \(SG(x) \not=0\) ,这是个必胜态。
有向图游戏的和
设 \(G_1,G_2,\dots,G_m\) 是 \(m\) 个有向图游戏,定义有向图游戏 \(G\) ,它的行动规则是任选某个有向图游戏 \(G_i\) ,并在 \(G_i\) 上行动一步。 这样的 \(G\) 被称为有向图游戏 \(G_1,G_2,\dots,G_m\) 的和。
有向图游戏的和的 \(SG\) 函数值等于它包含的各个子游戏 \(SG\) 函数值的异或和,即
SG 定理
有向图游戏的某个局面必胜,当且仅当该局面对应节点的 \(SG\) 函数值大于 \(0\)。
有向图游戏的某个局面必败,当且仅当该局面对应节点的 \(SG\) 函数值等于 \(0\)。
同理,对于一个有向图游戏的和,若 \(SG(G) = SG(G_1) \ \hat{} \ SG(G_2) \ \hat{} \ \dots \ \hat{} \ SG(G_m) > 0\) ,先手必胜,反之先手必败。
证明方法类似于 nim 博弈的证明,故略。
在敲代码时,我们往往利用这个定理,采用记忆化搜索的形式来求 \(SG\) 函数。
这里给出 POJ2311 cutting game 的正解 code
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 2e2 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int n,m;
int f[N][N];
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
il int SG(int x,int y)
{
if(f[x][y] != -1) return f[x][y];
set <int> S;
for(re int i=2;i<=x-2;i++) S.insert(SG(i,y)^SG(x-i,y));
for(re int j=2;j<=y-2;j++) S.insert(SG(x,j)^SG(x,y-j));
for(re int i=0;;i++) if(!S.count(i)) return f[x][y] = f[y][x] = i;
}
il void Main()
{
if(SG(n,m)) puts("WIN");
else puts("LOSE");
}
signed main()
{
memset(f , -1 , sizeof f);
while(scanf("%d %d",&n,&m) != EOF) Main();
return 0;
}
SG游戏的拓展变形
Anti-SG 游戏
先从 Anti-nim 讲起
Anti-nim 游戏
\(n\) 堆石子,两个人可以从任意一堆石子中拿任意多个石子,不能不拿,拿走最后一个石子的人 失败,问先手必胜条件。
为什么叫反 nim 游戏,就是最终的胜利条件反了过来。
结论:先手必胜当且仅当:
(1): 每个堆的石子数都为 \(1\) 且游戏的 SG 值为 \(0\) ,其实就是有偶数堆。
(2):有些堆的石子数 \(>1\) 且游戏的 SG 值不为 \(0\)
证明:
考虑一次游戏中会遇到三种情况:
-
每个堆的石子都为 \(1\) :
如果有奇数堆,那么最后肯定剩下一个给先手,先手必败;反之,如果有偶数堆,最后一堆就留给了后手,后手必败。
-
只有一个堆的石子 \(>1\) :
这时先手是必胜的。考虑一个构造:如果除了这一堆还有奇数堆,先手就可以把这一堆拿完,这样下次的先手就是总游戏的后手,它面临着必败局面,那么此时总游戏的先手就是必胜的;如果除了这一堆还有偶数堆,总游戏的先手就可以把这一堆拿的只剩下 \(1\) 个,同理这样也是必胜的。
-
至少两堆的石子数 \(>1\)
当总游戏的 \(SG\) 为 \(0\) 时,先手必败;反之,先手必胜。
类似于 nim 博弈的,我们可以证明出当石子的异或值等于 \(0\) 时,无论怎么拿都会使得异或值 \(>0\) ,这属于必败态到必胜态的转移;而异或值 \(>0\) 时,也总会存在一种情况使得异或值 \(=0\) ,这符合必胜态到必败态的转移。
我们不断进行操作,容易发现,总会有一个时刻变成了情况 \(2\) ,而情况 \(2\) 的异或值肯定不是 \(0\) ,所以它一定是由异或值为 \(0\) 的情况转移过来的。因为情况 \(2\) 是必胜态,所以异或值为 \(0\) 的就是必败态;反之,就是必胜态。
Anti-SG 游戏
Anti-SG游戏规定,决策集合为空的游戏者赢。其余的规则与 SG 游戏相同。
上一部分的推导仅对于 Anti-nim 游戏成立。因为 Anti-nim 游戏中 SG 值为 \(0\) 的一定是终止局面,而有向图游戏中则不一定了。
这里也有一个定理:SJ 定理
内容:对于任意一个 Anti-SG 游戏,如果我们规定:当局面中所有的单一游戏的 SG 值为 \(0\) 时,游戏结束,则先手必胜当且仅当:
-
游戏的 SG 函数值不为 \(0\) 且游戏中某个单一游戏的 SG 函数值大于 \(1\)
-
游戏的 SG 函数值为 \(0\) 且游戏中没有任意一个单一游戏的 \(SG\) 函数值大于 \(1\)
感性证明一下:类比刚才推导 Anti-nim 游戏的过程,第二个结论其实就类似于 Anti-nim 中每堆石子个数都是 \(1\) 的情况。第一个结论也能转移到第二个结论。具体的可以看this。
Multi-SG 游戏
还是从 nim 游戏的拓展出发。
Multi-nim 游戏
有 \(n\) 堆石子,两个人可以从任意一堆石子中拿任意多个石子(不能不拿),或者把一堆石子数量不少于 \(2\) 的石子堆分成两堆不为空的石子堆,没法拿的人失败。问必胜状态。
Multi-nim 有两种操作。其中操作一是平凡的,操作二就是把一个单一游戏分裂成两个单一游戏。根据 SG 定理,我们可以通过异或运算把两个游戏连接到一起,作为一个后继状态的 SG 值。
举个栗子,\(\text{SG}(3)\) 的后继状态有 \(\{(0),(1),(2),(1,2)\}\) ,后面的 \((1,2)\) 就是分开的情况,其余就是拿走的情况,它们的 \(\text{SG}\) 值分别为 \(\{0,1,2,3\}\) ,前面 \(3\) 个值就是推出来的,后面这个 \(3\) 其实就是 \(\text{SG(1)} \ \hat{} \ \text{SG(2)} = 1 \ \hat{} \ 2 =3\) 这么来的。所以 \(\text{SG(3)} = \text{mex}\{0,1,2,3\} = 4\)。
并且 Multi-nim 这种游戏还有一个妙妙的性质。
性质比较奇妙,建议背过。
背不过就妙妙打表。
#include<bits/stdc++.h>
//#define int long long
#define ll long long
#define next nxt
#define re register
#define il inline
const int N = 5e5 + 5;
const int M = 5e2 + 5;
using namespace std;
int max(int x,int y){return x > y ? x : y;}
int min(int x,int y){return x < y ? x : y;}
int SG[N];
il int read()
{
int f=0,s=0;
char ch=getchar();
for(;!isdigit(ch);ch=getchar()) f |= (ch=='-');
for(; isdigit(ch);ch=getchar()) s = (s<<1) + (s<<3) + (ch^48);
return f ? -s : s;
}
set <int> s;
signed main()
{
SG[0] = 0 , SG[1] = 1;
for(re int i=2;i<=500;i++)
{
s.clear();
for(re int j=1;j<=i;j++) s.insert(SG[i-j]);
for(re int j=1;j<i;j++) s.insert(SG[j] ^ SG[i-j]);
for(re int j=0;;j++) if(!s.count(j)) { SG[i] = j; break; }
}
for(re int i=0;i<=500;i++) cout << "SG[" << i << "]=" << SG[i] << "\n";
return 0;
}
Multi-SG 游戏
类似与 Multi-nim 的,我们定义 Multi-SG 游戏
Multi-SG 游戏规定,在符合拓扑原则的前提下,一个单一游戏的后继可以为多个单一游戏;Multi-SG 的其他规则与 SG 游戏相同。
其中单一游戏分为多个单一游戏,可以类比地想成是将当前这个堆的石子分成多堆石子。
对于一个状态来说,不同的划分方法会产生多个不同的后继,而在一个后继中可能含有多个独立的游戏。
就比如刚才的例子,\((1,2)\) 算是一个后继,但这一个后继里包含着多个独立的游戏,那么这个后继的 SG 函数值就是多个独立游戏的 SG 的异或和。
更书面化一点
结论:一个后继状态的 SG 值即为后继状态中所有独立游戏的异或和
该状态的 SG 函数值即为后继状态的 SG 函数值中未出现过的最小值
Every-SG 游戏
\(n\) 个游戏,每次每个能移动的游戏都需要移动,不能移动任何游戏的人输,求先手必胜的条件。
实质上是不论你在哪个游戏上赢与否,只要整个游戏的最后一步是你走的,你就是赢家。
为了保证最优,那肯定是能赢的必须赢下来,这样才能最大化最终赢的可能。
因为两个人都采取最优策略,因此,当一个人知道某个游戏一定会输的时候,它一定会尽力缩短这个游戏的时间;当他知道某一个游戏一定会赢的时候,一定会尽力延长游戏的时间,因为只有这个游戏越往后拖,最后一步就越有可能发生在这个游戏上。
Every-SG 游戏和普通 SG 游戏不同在于它多了一维时间。
对于 SG 值为 \(0\) 的点,我们需要知道最少需要多少步才能走到结束;对于 SG 值不为 \(0\) 的点,我们需要知道最多需要多少步结束。
我们用 \(\text{step}\) 变量来记录一下。
Every-SG 也有一个定理:
对于 Every-SG 游戏先手必胜当且仅当单一游戏中最大的 \(\text{step}\) 为奇数。
挺显然的。最大的单一游戏步数如果是奇数的话那么肯定是先手进行的最后一步,否则一定是对手取走的。
nim 游戏扩展
阶梯型 nim 游戏
有 \(1\sim n\) 级台阶,第 \(i\) 级台阶上摆放 \(a_i\) 个石子,每次操作可将第 \(k\) 级台阶上的石子移一些到第 \(k-1\) 级台阶上,移到第 \(0\) 级台阶(地面)的石子不能再移动。如果一个人没有石子可以移动,他就输了,问先手是否必胜。
还是先放结论。
若奇数台阶上的 \(a_1 \ \hat{} \ a_3 \ \hat{} \ a_5 \hat{} \dots \not= 0\) ,则先手必胜,反之,先手必败。
简略证明:
首先末态一定是 \(a_1 \ \hat{} \ a_3 \ \hat{} \ a_5 \hat{} \dots = 0\) , 那么如果初态 \(a_1 \ \hat{} \ a_3 \ \hat{} \ a_5 \hat{} \dots \not= 0\) ,就一定存在一种方式将某奇数台阶的石子移动到偶数台阶上使得异或和 \(= 0\) 。这样,不管后手的人是把奇数台阶的移动到偶数台阶还是相反,先手都一定存在一种方案使得异或和为 \(0\) ,这样就一定能转移到末态,先手就赢了!
Moore's NimK
两个人玩取石子游戏,共有 \(n\) 堆石子,每个人每次可以从不超过 \(k\) 堆石子里面取任意多个石子(不能不取),不能取的人输。问先手必胜条件。
依旧先放结论。
将每一个数写成二进制形式,则如果每一位上 \(1\) 的个数都是 \(k+1\) 的倍数,则先手必败,否则先手必胜。
证明:
必败态只能到必胜态是显然的。你无论取多少一定会改变一个二进制位上 \(1\) 的个数,使其不为 \(k+1\) 的位数。
接下来考虑必胜态可以到必败态。我们从二进制的高位到低位考虑。假设我们找到了第一个二进制位下 \(1\) 的和不是 \((k+1)\) 倍数的情况,那么这一位上的 \(1\) 的和就能被写成 \(t(k+1) + r(1 \leq r \leq k)\) ,我们给这 \(r\) 个数做一下修理,使得这一位为 \(0\) ,同时把它后面的位都变为 \(1\)。但是这还没完,再往下找,可能有一位上的 \(r\) 我们称之为 \(r'\) 是要 \(>r\) 的,我们就可以再修改 \(r'-r\) 个数,使得这一位上也是 \((k+1)\) 的倍数,并让它后面的也同时为 \(1\)。这样迭代下去,最多会改变 \(k\) 个数,是可以的,证毕。
总结
以上基本就是博弈论的全部内容,当然还有无向图删边问题、动态减法问题之类的没有涉及。但是通过这么多我们已经能够得出解决博弈论问题的一般思路:打表找规律!建出有向图游戏暴力跑一跑找结论,大胆猜想,小心分析。一般结论跟异或和二进制有关,可以往这方面考虑。


