组合数学

前置知识

加法原理

若完成一件事的方法有 \(n\) 类，其中第 \(i\) 类方法有 \(a_i\) 种不同的方法，且这些方法互不重合，那么完成这件事共有 \(a_1 + a_2 + \dots + a_n\) 种方法。

乘法原理

若完成一件事需要 \(n\) 个步骤，其中第 \(i\) 个步骤有 \(a_i\) 种不同的方法，且这些步骤互不干扰，则完成这件事共有 \(a_1 \times a_2 \times \dots \times a_n\) 种方法。

于我的观点，加法原理适用于一个问题的不同解，而乘法原理就是把一个问题不同步骤的不同解乘起来了。

抽屉原理

把 \(n+1\) 个元素划分至 \(n\) 个集合 \(A_1,A_2,\dots,A_n\) 中，则至少存在一个集合 \(A_i\)，使得 \(A_i\) 这个集合中的元素个数 \(\ge 2\)。

没错，这就是抽屉原理，也叫鸽巢原理。

我们拓展一下。

把 \(nm+1\) 个元素划分至 \(n\) 个集合 \(A_1,\dots,A_n\) 中，则至少存在一个集合 \(A_i\)，使得 \(A_i\) 这个集合中的元素个数 \(\ge m+1\)。

更普遍地。

把 \(m(\ge n)\) 个元素划分至 \(n\) 个集合 \(A_1,\dots,A_n\) 中，则至少存在一个集合 \(A_i\)，使得 \(A_i\) 这个集合中的元素个数 \(\ge \lfloor \frac{m}{n} \rfloor\)。

容斥原理

在计数时，必须注意没有重复，没有遗漏。为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

集合的并

设 \(U\) 中元素有 \(n\) 种不同的属性，第 \(i\) 种属性称为 \(P_i\)，拥有属性 \(P_i\) 的元素构成集合 \(S_i\)，那么

\[\Bigg|\bigcup_{i=1}^nS_i\Bigg|=\sum_i|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j \cap S_k|-\dots \]

\[+(-1)^{m-1}\sum_{a_i<a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|+\dots+(-1)^{n-1}|S_1\cap\dots\cap S_n| \]

即

\[\Bigg|\bigcup_{i=1}^nS_i\Bigg|=\sum_{m=1}^n (-1)^{m-1}\sum_{a_i<a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg| \]

意义：集合的并等于集合的交的交错和（奇正偶负）。

集合的交

集合的交等于全集减去补集的并。

\[\Bigg|\bigcap_{i=1}^nS_i\Bigg|=|U|-\Bigg|\bigcup_{i=1}^n\overline{S_i}\Bigg| \]

右边补集的并容易用容斥原理求解，这就求出了集合的交。

排列组合

排列

定义

从 \(n\) 个不同元素中依次取出 \(m\) 个元素排成一列，产生的不同排列的数量。(\((1,2)\)和\((2,1)\)算两种方案)，记作\(A_n^m(m \leq n)\)

\(A_n^1\) 等于从 \(n\) 个数中选 \(1\) 个数的方法总数，显然 \(A_n^1 = n\)

\(A_n^2\) 等于从 \(n\) 个数中选 \(2\) 个数的方法总数。我们可以分两步处理：第一步，选一个数放在第一个位置，有 \(n\) 种选法；第二步，选一个数放在第二个位置，因为已经用了一个了，所以还有 \(n-1\) 个数，因此有 \(n-1\) 种选法。根据乘法原理，一共有 \(n(n-1)\) 种选法，因此 \(A_n^2 = n(n-1)\)

类似的，我们可以知道

\[A_n^3 = n(n-1)(n-2) \]

\[A_n^4 = n(n-1)(n-2)(n-3) \]

一般的，我们可以得到它的通项公式：

\[A_n^m = \underbrace{n(n-1)(n-2)\dots (n-(m-1))}_{m\text{项}} \]

用一种更简便的方法来表示

\[A_n^m = n(n-1)(n-2)\dots (n-(m-1)) \]

\[= \frac{n(n-1)(n-2)\dots (n-(m-1)) \times (n-m)\times \dots .\times 1}{(n-m)\times \dots .\times 1} \]

\[= \frac{n!}{(n-m)!} \]

为了保证 \(n=m\) 的时候也有解，我们规定 \(0! = 1\)。

性质

\[nA_{n-1}^{m-1} = A_n^m \]

证明：

\[nA_{n-1}^{m-1} = \frac{(n-1)!\times n}{(n-1 - (m-1))!} \]

\[= \frac{n!}{(n-m)!} = A_n^m \]

\[mA_{n-1}^{m-1} + A_{n-1}^m = A_n^m \]

证明：

\[mA_{n-1}^{m-1} + A_{n-1}^m = \frac{m(n-1)!}{(n-m)!} + \frac{(n-1)!}{(n-m-1)!} \]

\[= \frac{m(n-1)! + (n-m)(n-1)!}{(n-m)!} \]

\[= \frac{n!}{(n-m)!} = A_n^m \]

组合

定义

从 \(n\) 个不同元素中选 \(m\) 个组成一个集合，产生的不同集合的数量。（不考虑顺序,\((1,2)\)和\((2,1)\)算一种）

\(n\) 个不同对象中取出 \(m\) 个做排列，可以分成两个步骤完成：第一步，从 \(n\) 个不同对象中取出 \(m\) 个，有 \(C_n^m\) 种选法；第二步，将选出的 \(m\) 个对象做全排列，有 \(A_m^m\) 种选法，由乘法原理得：\(C_n^m \times A_m^m = A_n^m\)。

由此我们推出组合的通项公式：

\[C_n^m = \frac{A_n^m}{A_m^m} = \frac{\frac{n!}{(n-m)!}}{m!} = \frac{n!}{m!(n-m)!} \]

性质

\[C_n^m = C_{n-1}^{m-1} + C_{n-1}^{m} \]

证明：从 \(n\) 个数选 \(m\) 个数，就等于选了第一个数，再从 \(n-1\) 个数中选 \(m-1\) 个数，和不选第一个数，从 \(n-1\) 个数中选 \(m\) 个的方案数总和。

这个其实看杨辉三角能很轻松的看出来，杨辉三角的第 \(n\) 行的第 \(m\) 列对应的数就是 \(C_n^m\)

\[C_n^m = C_n^{n-m} \]

证明：

\[C_n^{n-m} = \frac{n!}{[n-(n-m)]!(n-m)!} \]

\[= \frac{n!}{m!(n-m)!} = C_n^m \]

感性理解，你每次从 \(n\) 个物品中选 \(m\) 个物品，那么必然剩下 \(n-m\) 个物品，每种选取 \(n\) 个物品的方案和选取剩下的 \(n-m\) 个物品的方案是一一对应的。

\[C_{n+m+1}^{m} = \sum_{i=0}^mC_{n+i}^i \]

证明：首先对性质 \(1\) 变形：\(C_n^m + C_n^{m-1}=C_{n+1}^{m}\) ，并且我们知道 \(C_n^0 = C_{n+1}^0 = 1\) ， 那么就有

\[\sum_{i=0}^mC_{n+i}^i = C_n^0 + C_{n+1}^1 + \dots + C_{n+m}^m \]

替换第一项

\[= C_{n+1}^0 + C_{n+1}^1 + \dots + C_{n+m}^m \]

合并

\[= C_{n+2}^1 + C_{n+2}^2 + \dots + C_{n+m}^m \]

以此类推

\[= C_{n+m+1}^m \]

\[C_n^m \cdot C_m^r =C_n^r \cdot C_{n-r}^{m-r} \]

证明：

\[C_n^m \cdot C_m^r = \frac{n!}{m!(n-m)!}\cdot \frac{m!}{r!(m-r)!} \]

\[= \frac{n!}{r!(n-m)!(m-r)!} \]

分子分母同乘\((n-r)!\)

\[= \frac{n!}{r!(n-r)!}\cdot \frac{(n-r)!}{(m-r)!(n-m)!} = C_n^r \cdot C_{n-r}^{m-r} \]

运用组合的思想理解一下，左边就是先从 \(n\) 个中选 \(m\) 个，再从 \(m\) 个选 \(r\) 个的方案数。

这就等价于右边先从 \(n\) 个中选 \(r\) 个，再从剩下的 \(n-r\) 个中选没被选上的 \(m-r\) 个。

\[m \cdot C_n^m = n \cdot C_{n-1}^{m-1} \]

证明：由性质 \(4\) 得

\[m \cdot C_n^m = C_m^1 \cdot C_n^m \]

\[= C_n^1 \cdot C_{n-1}^{m-1} = n \cdot C_{n-1}^{m-1} \]

6.二项式定理的特殊形式

\[\sum_{i=0}^nC_n^i\cdot x^i = (x+1)^n \Rightarrow \]

\[C_{n}^{0} + C_{n}^{1} + C_{n}^{m} + \dots + C_{n}^{n} = \sum_{i=0}^nC_n^i = 2^n \]

证明：取 \(x=1\) ，即有 \(\sum_{i=0}^nC_n^i = 2^n\) , 至于二项式定理，一会再说明。也可以从另一个方面去想， 从 \(n\) 个元素中取出若干个元素组成一个集合，有 \(n+1\) 类方法，分别是取出 \(0,1,2,\dots,n+1\) 个，根据加法原理，共有 \(C_n^0 + C_n^1 + \dots +C_n^n\) 种方法；又根据乘法原理，每个数可以选或不选，所以一共有 \(2^n\) 种方法。二者相等，所以公式成立。

\[\sum_{i=0}^n(-1)^iC_n^i = 0 \]

证明：当 \(m\) 为奇数时，由性质 \(2\) 可得，两项一一对应和为 \(0\) ，显然成立；当 \(m\) 为偶数时，利用 \(C_n^0 = C_{n-1}^0 , C_m^m = C_{m-1}^{m-1}\) 替换，再用递推式得到

\[\sum_{i=0}^n(-1)^iC_n^i = C_n^0 - C_n^1 + C_n^2 - \dots -C_n^{n-1} +C_n^n \]

\[= C_{n-1}^0 - C_n^1 + \dots - C_n^{n-1}+C_{n-1}^{n-1} \]

\[= C_{n-1}^0 - (C_{n-1}^0 + C_{n-1}^1) + \dots - (C_{n-1}^{n-2} + C_{n-1}^{n-1}) + C_{n-1}^{n-1} = 0 \]

\[C_n^0 + C_n^2 + C_n^4 + \dots =C_n^1 + C_n^3 + C_n^5 + \dots = 2^{n-1} \]

证明：由性质 \(7\) 显然可得。

\[C_{n+m}^{r} = \sum_{i=0}^r C_n^iC_m^{r-i} \]

证明：在 \((n+m)\) 个数中选 \(r\) 个数，在前 \(n\) 中选 \(i\) 个数的方案有 \(C_n^i\) 种，在后 \(m\) 个里选 \((r-i)\) 个数的方案有 \(C_m^{r-i}\) 种，相乘并求和即可得到该式。

\[\sum_{i=0}^n(C_n^i)^2 = C_{2n}^n \]

证明：由性质 \(9\) 取 \(m=n\) 即可得。

\[\sum_{i=1}^nC_n^i \cdot i = \sum_{i=0}^n C_n^i \cdot i = n\cdot 2^{n-1} \]

证明：把左边展开得

\[\sum_{i=1}^nC_n^i \cdot i = \sum_{i=1}^n\frac{n!}{(n-i)!(i-1)!} \]

\[= n \cdot \sum_{i=1}^n\frac{(n-1)!}{(n-i)!(i-1)!} \]

\[= n \cdot \sum_{i=1}^{n}C_{n-1}^{i-1} \]

\[= n \cdot \sum_{i=0}^{n-1} C_{n-1}^i = n \cdot 2 ^{n-1} \]

\[\sum_{i=1}^nC_n^i \cdot i^2 = \sum_{i=0}^n C_n^i \cdot i^2 = n(n+1)\cdot 2^{n-2} \]

证明：类似于11

\[\sum_{i=1}^nC_n^i \cdot i^2 = \sum_{i=1}^n\frac{n!\cdot i}{(n-i)!(i-1)!} \]

把 \(i\) 拆成 \(i-1\) 和 \(1\)

\[= n \cdot \sum_{i=1}^n\frac{(n-1)!}{(n-i)!(i-1)!} + n \cdot \sum_{i=1}^n\frac{(n-1)!(i-1)}{(n-i)!(i-1)!} \]

\[= n2^{n-1} + n\cdot \sum_{i=1}^{n}C_{n-1}^{i-1}(i-1) \]

由性质5\((m \cdot C_n^m = n \cdot C_{n-1}^{m-1})\)

\[= n2^{n-1} + n \cdot (n-1) \cdot \sum_{i=2}^{n} C_{n-2}^{i-2} \]

\[ = n2^{n-1} + n \cdot (n-1) \cdot 2^{n-2} \]

\[= 2n \cdot 2^{n-2} + n \cdot(n-1) \cdot 2^{n-2} = n(n+1)\cdot2^{n-2} \]

组合数取模

\[C_n^m \ \text{mod} \ p \]

1. $ 1 \leq n,m \leq 1000$ , \(p\) 为任意实数：显然可以用组合数的递推式 \(C_n^m = C_{n-1}^{m} + C_{n-1}^{m-1}\) 来 \(O(n^2)\) 递推。

2. \(1 \leq n,m \leq 10^6\) ，\(p\) 为质数且 \(p > 10^6\)：\(O(n)\)预处理 \(i! \ \text{mod} \ p\)，然后费马小定理求 \(m!\) 的逆元和 \((n-m)!\) 的逆元，最后一相乘即可。预处理 \(O(n)\) ，询问 \(O(\log n)\)。

   当然也可以 \(O(n\log n)\) 预处理 \(i!\) 和 \(i!\) 的逆元，询问的时候 \(O(1)\) 的 ans = jc[n] * inv[m] * inv[n-m] % p 即可。

3. 若要对 \(C_n^m\) 进行高精度计算。有类似于阶乘分解那一题的计数原理，计算出每个质因子的个数，然后上减下，把分母消去，最后剩下的质因子乘起来，就能得到答案。

4. 若 \(p\) 为质数，\(1 \leq n,m \leq 10^9 , p \leq 10^5\) : 应用卢卡斯定理，将 \(n,m\) 转化为 \(p\) 进制数。一会细讲。

后言

还有一些常见的方法，具体见高中数学瞎记

二项式定理

\[(x+y)^n = \sum_{k=0}^{n}C_n^kx^{n-k}y^k \]

感性证明：

\[(x+y)^n \]

也就是

\[\underbrace{(x+y)\cdot(x+y)\cdot(x+y)\cdot\dots\cdot (x+y)}_{n\text{项}} \]

如果每个 \((x+y)\) 出来的都是 \(x\) ，那么就是 \(x^ny^0\) ，如果出来了 \(n-1\) 个 \(x\) ，\(1\) 个 \(y\) ，那么就是 \(x^{n-1}y^0\) ,那么总共就是 \(x^ny^0 + x^{n-1}y^1 + \dots + x^1y^{n-1}+x^0y^n\) 这样一个形式。

接下来考虑系数。从\(n\) 个 \((x+y)\) 中选 \(0\) 个 \(y\) ，显然方案数就是 \(C_n^0\) ；同理，选一个 \(y\) 就是 \(C_n^1\) ，因为选 \(x\) 跟选 \(y\) 的方案是一一对应的。所以最后的系数就是

\[C_n^0x^ny^0 + C_n^1x^{n-1}y^1 + \dots + C_n^{n-1}x^1y^{n-1}+C_n^nx^0y^n \]

的形式，写成通项公式就是

\[(x+y)^n = \sum_{k=0}^{n}C_n^kx^{n-k}y^k \]

其中 \(C_n^k\) 就被称为二项式系数。

拓展一下， \((ax+by)^n\) 就是

\[(ax+by)^n = \sum_{k=0}^{n}C_n^ka^{n-k}x^{n-k}b^ky^k \]

所以 \(x^{n-k}y^k\) 的系数就是 \(C_n^ka^{n-k}b^k\) ，而它的二项式系数还是 \(C_n^k\) 。

多重集

多重集的排列组合

多重集就是有重复元素的广义的，不满足互异性的集合。也就是 multiset。

寄，来不及学了，不学了。

给两个公式得了。

多重集的排列数

设 \(S = \{n_1 \times a_1,n_2 \times a_2,\dots ,n_k\times a_k\}\) 是由 \(n_1\) 个 \(a_1\) ，\(n_2\) 个 \(a_2\dots\) ，\(n_k\) 个 \(a_k\) 组成的多重集，记 \(n = n_1 + n_2 + \dots +n_k\) 。 \(S\) 的全排列个数为

\[\frac{n!}{n_1!n_2!\dots n_k!} \]

多重集的组合数

设 \(S = \{n_1 \times a_1,n_2 \times a_2,\dots ,n_k\times a_k\}\) 是由 \(n_1\) 个 \(a_1\) ，\(n_2\) 个 \(a_2\dots\) ，\(n_k\) 个 \(a_k\) 组成的多重集，记 \(n = n_1 + n_2 + \dots +n_k\) 。
设整数 \(r \leq n_i(\forall i \in [1,k])\)。从 \(S\) 中取出 \(r\) 个元素组成一个多重集（不考虑元素的顺序），产生的不同多重集的数量为 \(C_{k+r-1}^{k-1}\) 。

Lucas 定理

适用情形

如上文所述，如果遇到 \(n\) 和 \(m\) 都很大的组合数取模问题，其中 \(1\leq m\leq n\le10^{18},1\leq q \leq 10^5\) ，并且保证 \(p\) 为质数的时候，就可以使用 Lucas 定理了。

内容

\[C_n^m \equiv C_{n/p}^{m/p}C_{n \ \text{mod} \ p}^{m \ \text{mod} \ p}(\text{mod} \ p) \]

证明

引理 \(1\) ：\(C_p^x \equiv 0(\text{mod} \ p) , 0 < x < p\)

因为

\[C_p^x = \frac{p!}{x!(p-x)!} = \frac{p(p-1)!}{x(x-1)!(p-x)!} = \frac{p}{x}C_{p-1}^{x-1} \]

则有

\[C_p^x = p \cdot inv(x) C_{p-1}^{x-1} \equiv 0(\text{mod} \ p) \]

其中 \(inv(x)\) 表示 \(x\) 在模 \(p\) 意义下的逆元，因为 \(p\) 为质数且 \(x<p\) ，所以逆元一定存在。

引理 \(2\)：\((1+x)^p \equiv 1 + x^p(\text{mod} \ p)\)

由二项式定理得 \((1+x)^p = \sum_{i=0}^p C_p^ix^i\) 。由引理 \(1\) 能得到，除了 \(i=0 ,i = p\) 两项，其余模 \(p\) 都是 \(0\) ， 而 \(i=0\) 这一项就是 \(C_p^0x^0 = 1 \equiv 1(\text{mod} \ p)\) ，\(i=p\) 这一项是 \(C_p^px^p = x^p \equiv x^p(\text{mod} \ p)\) ，加上那些中间模 \(p\) 等于 \(0\) 的项，就是 \((1+x)^p \equiv 1 + x^p(\text{mod} \ p)\)

真正的证明：

令 \(n = ap + b , m = cp + d\)

\((1+x)^n = \sum_{i=0}^n C_n^ix^i(\text{mod} \ p)\) ，这是式子 \(1\) ；

\((1+x)^n = (1+x)^{ap+b} = ((1+x)^p)^a\cdot (1+x)^b\)

\(\equiv (1 + x^p)^a \cdot (1+x)^b = \sum_{i=0}^a C_a^ix^{ip} \cdot \sum_{j=0}^b C_b^jx^j(\text{mod} \ p)\)

这是式子 \(2\) 。

式子 \(1\) 中 \(x^m\) 这一项的系数是 \(C_n^m\)

式子 \(2\) 中 \(x^m = x^{cp}x^d\) 的系数为 \(C_a^cC_b^d\)

所以就有 \(C_n^m \equiv C_a^cC_b^d(\text{mod} \ p)\)

即

\[C_n^m \equiv C_{n/p}^{m/p}C_{n \ \text{mod} \ p}^{m \ \text{mod} \ p}(\text{mod} \ p) \]

Catalan 数列（卡特兰数）

定义

给定 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) ，它们随机排成长度为 \(2n\) 的序列，满足任意前缀 \(0\) 的个数都不少于 \(1\) 的个数的序列的数量为

\[Cat_n = C_{2n}^n - C_{2n}^{n-1} = \frac{C_{2n}^n}{n+1} \]

证明：

令 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 随机排成一个 \(2n\) 的序列 \(S\)，如果说 \(S\) 不满足任意前缀中 \(0\) 的个数都不少于 \(1\) 的个数，那么一定存在一个最小的位置 \(2p+1 \in [1,2n]\) ，使得 \(S[1\sim 2p+1]\) 有 \(p\) 个 \(0\) ， \(p+1\) 个 \(1\) 。再把 \(S[2p+2\sim 2n]\) 的所有数字取反（\(0\) 变 \(1\) ，\(1\) 变 \(0\)）后，包含 \(n-p-1\) 个 \(0\) 和 \(n-p\) 个 \(1\) ，于是我们得到了一个由 \(n-1\) 个 \(0\) ，\(n+1\) 个 \(1\) 组成的序列。

同理，令 \(n-1\) 个 \(0\) 和 \(n+1\) 个 \(1\) 随机排成一个序列 \(S'\) ，那么一定存在一个最小的位置 \(2p'+1 \in [1,2n]\) ，使得 \(S'[1\sim 2p'+1]\) 有 \(p'\) 个 \(0\) ， \(p'+1\) 个 \(1\) 。再把 \(S[2p'+2\sim 2n]\) 的所有数字取反后，就得到了一个由 \(n\) 个 \(0\) ，\(n\) 个 \(1\) 组成的，至少存在一个前缀 \(0\) 比 \(1\) 多的序列。

斯特林数

前置知识

圆排列

定义：\(n\) 个不同元素围成一圈的个数，叫做圆排列数，记作 \(Q_n^n\)。

计算公式：
考虑其中已经排好的一圈，\(n\) 个元素之间有 \(n\) 个空，我们从这不同的 \(n\) 个空断开，每个空断开后形成了不同的线排列，总共 \(n\) 种。

这就说明圆排列是把 \(n\) 种线排列整合成 \(1\) 种了，于是我们得到圆排列的计算公式：

\[Q_n^n \times n = A_n^n \]

\[Q_n^n = \frac{A_n^n}{n}=(n-1)! \]

例如，\(3\) 个不同元素的圆排列数为 \((3-1)!=2\) 种。

$\text{from} \ $董晓算法

我们发现每个圆排列断开后形成 \(n\) 个线排列，这也就是我们计算公式的来源。

另一个公式：

从 \(n\) 个不同元素中，选 \(m\) 个元素围成一圈的圆排列数，记作 \(Q_n^m\)，那么就有

\[Q_n^m = C_n^mQ_m^m = \frac{n!}{m(n-m)!} \]

错位排列

定义：错位排列是指没有任何元素出现在其有序位置的排列，对于 \(1\sim n\) 的排列 \(P\)，如果满足 \(P_i \not=i\)，则称 \(P\) 是 \(n\) 的错位排列。

错位排列数：表示元素个数为 \(n\) 的错位排列个数，记作 \(D_n\)。

\(D_1 = 0\)，因为 \(1\) 只能在这一个位置；

\(D_2 = 1\)，即 \(\{2,1\}\)；

\(D_3 = 2\)，即 \(\{2,3,1\},\{3,1,2\}\)。

以此类推。

递推公式：

\[D_n = (n-1)(D_{n-1}+D_{n-2}) \]

考虑如何递推，我们把它放在一个实际情况中进行理解。

假设我们有 \(n\) 封信，编号 \(1\sim n\)，现在我们把这 \(n\) 封信放在编号是 \(1\sim n\) 的信封中，要求信封的编号与信的编号不一样。问有多少种不同的方法。

考虑第 \(n\) 个信封，我们暂时把第 \(n\) 封信放在第 \(n\) 个信封中，然后考虑哪些情况能通过一次操作就变成 \(n\) 位错排。

情况 \(1\) ：前面 \(n-1\) 个信封全部装错，那么第 \(n\) 封只需要与前面 \(n-1\) 个位置的信封交换即可，这样就有 \((n-1)D_{n-1}\) 种方法。

情况 \(2\) ：前面 \(n-1\) 个信封中有一个没装错其余的都装错了，那么第 \(n\) 封只需要和那个没装错的交换就行了，没装错的信封有 \(n-1\) 种可能，每种可能的其余 \(n-2\) 封信是错排的，所以总共就是 \((n-1)D_{n-2}\) 种情况。

分类加法加起来，我们便得到了

\[D_n = (n-1)(D_{n-1}+D_{n-2}) \]

第一类斯特林数（斯特林轮换数）

定义

将 \(n\) 个不同元素，划分为 \(m\) 个非空圆排列的方案数，记作 \(\begin{bmatrix}n\\m\end{bmatrix}\)。

递推公式

\[\begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix}n-1\\m-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\m\end{bmatrix} \]

放到实际情况下证明一下。

实际意义可以是 \(n\) 个人坐 \(m\) 张圆桌并且没有空圆桌的方案数。

考虑第 \(n\) 个人座位的情况：

1. 若单独坐一桌，前面的 \(n-1\) 个人就要坐到 \(m-1\) 张桌子上，方案数就是 \(\begin{bmatrix}n-1\\m-1\end{bmatrix}\)；

2. 若坐到已经有人的桌子上，就先让前 \(n-1\) 个人坐 \(m\) 张桌子上，第 \(n\) 个人可以坐到之前 \(n-1\) 个人中任意一个人的左边，不重不漏，这样的方案数就是 \((n-1)\begin{bmatrix}n-1\\m\end{bmatrix}\)。

分类加法，最后的方案数就是

\[\begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix}n-1\\m-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\m\end{bmatrix} \]

性质

\[n! = \sum_{i=0}^n\begin{bmatrix}n\\i\end{bmatrix} \]

每种排列都会对应着唯一一种置换。

第二类斯特林数（斯特林子集数）

定义

将 \(n\) 个不同元素，划分为 \(m\) 个非空子集的方案数，记作 \(\begin{Bmatrix}n\\m\end{Bmatrix}\)。

递推公式

\[\begin{Bmatrix}n\\m\end{Bmatrix} = \begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\m\end{Bmatrix} \]

还是放到实际情况下证明一下。

实际意义可以是 \(n\) 个人进 \(m\) 个房间并且没有房间是空的的方案数，这里人不同而房间是相同的。

考虑第 \(n\) 进房间的情况：

1. 若单独进一个房间，前面的 \(n-1\) 个人就要进 \(m-1\) 个房间里，方案数就是 \(\begin{Bmatrix}n-1\\m-1\end{Bmatrix}\)；

2. 若进已经有人的房间里，就先让前 \(n-1\) 个人进 \(m\) 个房间里，第 \(n\) 个人可以进 \(m\) 个房间中任意一个房间，不重不漏，这样的方案数就是 \(m\begin{Bmatrix}n-1\\m\end{Bmatrix}\)。

分类加法，最后的方案数就是

\[\begin{Bmatrix}n\\m\end{Bmatrix} = \begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\m\end{Bmatrix} \]

斯特林反演

直接给出式子

\[F(n) = \sum_{i=0}^n\begin{Bmatrix}n\\i\end{Bmatrix}G(i) \Longleftrightarrow G(n) = \sum_{i=0}^n(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}F(i) \]

证明不会，略。

还有两个反转公式

\[\sum_{k=m}^n(-1)^{n-k}\begin{bmatrix}n\\k\end{bmatrix}\begin{Bmatrix}k\\m\end{Bmatrix} = [m=n] \]

\[\sum_{k=m}^n(-1)^{n-k}\begin{Bmatrix}n\\k\end{Bmatrix}\begin{bmatrix}k\\m\end{bmatrix} = [m=n] \]

这个公式运用最多的就是普通幂和上升幂下降幂的转换。

下降幂

\[x^{\underline{k}} = x(x-1)\dots(x-k+1)=\frac{x!}{(x-k)!}=\frac{x!k!}{(x-k)!k!}=\binom{x}{k}k! \]

上升幂

\[x^{\overline{k}} = x(x+1)\dots(x+k-1)=\frac{(x+k-1)!}{(x-1)!}=\frac{(x+k-1)!k!}{(x-1)!k!}=\binom{x+k-1}{k}k! \]

普通幂转下降幂

\[x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}}=\sum_{k=0}^n\binom{x}{k}\begin{Bmatrix}n\\k\end{Bmatrix}k! \]

也就是说，第二类斯特林数是普通幂展开成下降幂的系数。

---

我们从组合的思想证明一下：

左边是将 \(n\) 个不同球放在 \(x\) 个不同盒子里，每个球有 \(x\) 种放法，所以共有 \(x^n\) 种方法。

而右边枚举非空盒子的个数 \(k\)，从 \(x\)个盒子中选出 \(k\) 个盒子，将 \(n\) 个球放在这 \(k\) 个盒子里，每个盒子不能为空，显然方案数就是第二类斯特林数。并且因为 \(k\) 个盒子互不相同，所以还要对这 \(k\) 个盒子进行一个全排列。

证毕。

---

我们还可以用数学归纳法加以证明，首先列两个要用到的式子。

\[\begin{Bmatrix}n\\k\end{Bmatrix} = \begin{Bmatrix}n-1\\k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\k\end{Bmatrix} \]

\[x^{\underline{k+1}}=x^{\underline{k}}(x-k)=x\cdot x^{\underline{k}}-k\cdot x^{\underline{k}} \]

证明：

首先对于 \(n=0,1\) ，式子显然成立。

当 \(n>1\) 时，

\[x^n = x\cdot x^{n-1}=x\sum_{k=0}^{n-1}\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}} \]

因为当 \(k=n\) 时右边这个式子为 \(0\)，所以我们更改一下 \(\sum\) 的上界。接着把 \(x\) 放进去，运用式子 \(2\)：

\[\begin{aligned} &=x\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}}\\ &=\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k+1}}+\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}kx^{\underline{k}}\\ &=\sum_{k=1}^n\begin{Bmatrix}n-1\\k-1\end{Bmatrix}x^{\underline{k}}+\sum_{k=1}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}}\\ &=\sum_{k=1}^n\Bigg(\begin{Bmatrix}n-1\\k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\k\end{Bmatrix}\Bigg)x^{\underline{k}}\\ &=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}} \end{aligned} \]

其中 \(k\) 下界的变化是因为当 \(k=n\) 时无意义，因此等效。

下降幂转普通幂

\[x^{\underline{n}}=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k \]

我们同样使用归纳法证明，并且同样再列两个要用到的式子。

\[\begin{bmatrix}n\\k\end{bmatrix} = \begin{bmatrix}n-1\\k-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\k\end{bmatrix} \]

\[x^{\underline{n}} = x^{\underline{n-1}}(x-n+1) \]

证明：

首先当 \(n=0,1\) 时，式子成立。

当 \(n>1\) 时，

\[x^{\underline{n}} = x^{\underline{n-1}}(x-n+1) \]

\[\begin{aligned} &=\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^k(x-n+1)\\ &=\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^{k+1}-\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^k(n-1)\\ &=\sum_{k=1}^n\begin{bmatrix}n-1\\k-1\end{bmatrix}(-1)^{n-k}x^{k}+\sum_{k=1}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k}x^k(n-1)\\ &=\sum_{k=1}^n\Bigg(\begin{bmatrix}n-1\\k-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\k\end{bmatrix}\Bigg)(-1)^{n-k}x^k\\ &=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k \end{aligned} \]

普通幂转上升幂

\[x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}(-1)^{n-k}x^{\overline{k}} \]

依然使用归纳法证明，这里略了。

上升幂转普通幂

\[x^{\overline{n}} = \sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k \]

还是归纳法，还是略。

总结四个变换

\[x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}} \]

\[x^{\underline{n}}=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k \]

\[x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}(-1)^{n-k}x^{\overline{k}} \]

\[x^{\overline{n}} = \sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k \]

咋记呢，首先我们发现 \(x^{\overline{k}} \ge x^k \ge x^{\underline{k}}\)，所以再由下降幂转普通幂，普通幂转上升幂的过程中，一定会有一个 \((-1)^{n-k}\)。

第一类斯特林数是从下降幂和上升幂转到普通幂用；第二类斯特林数是从普通幂转到下降米和上升幂用。

两种幂互相转化用到的斯特林数不同，然后记住第一个变化即可。

Prüfer 序列

小众乐子知识点。

引入

Prüfer 序列可以将一个带标号 \(n\) 个节点的无根树用 \([1,n]\) 中的 \(n-2\) 个整数表示。

其实就是完全图的生成树与数列之间的双射，因为这个性质，所以 Prüfer 数列常用在组合计数问题上。

对树建立 Prüfer 序列

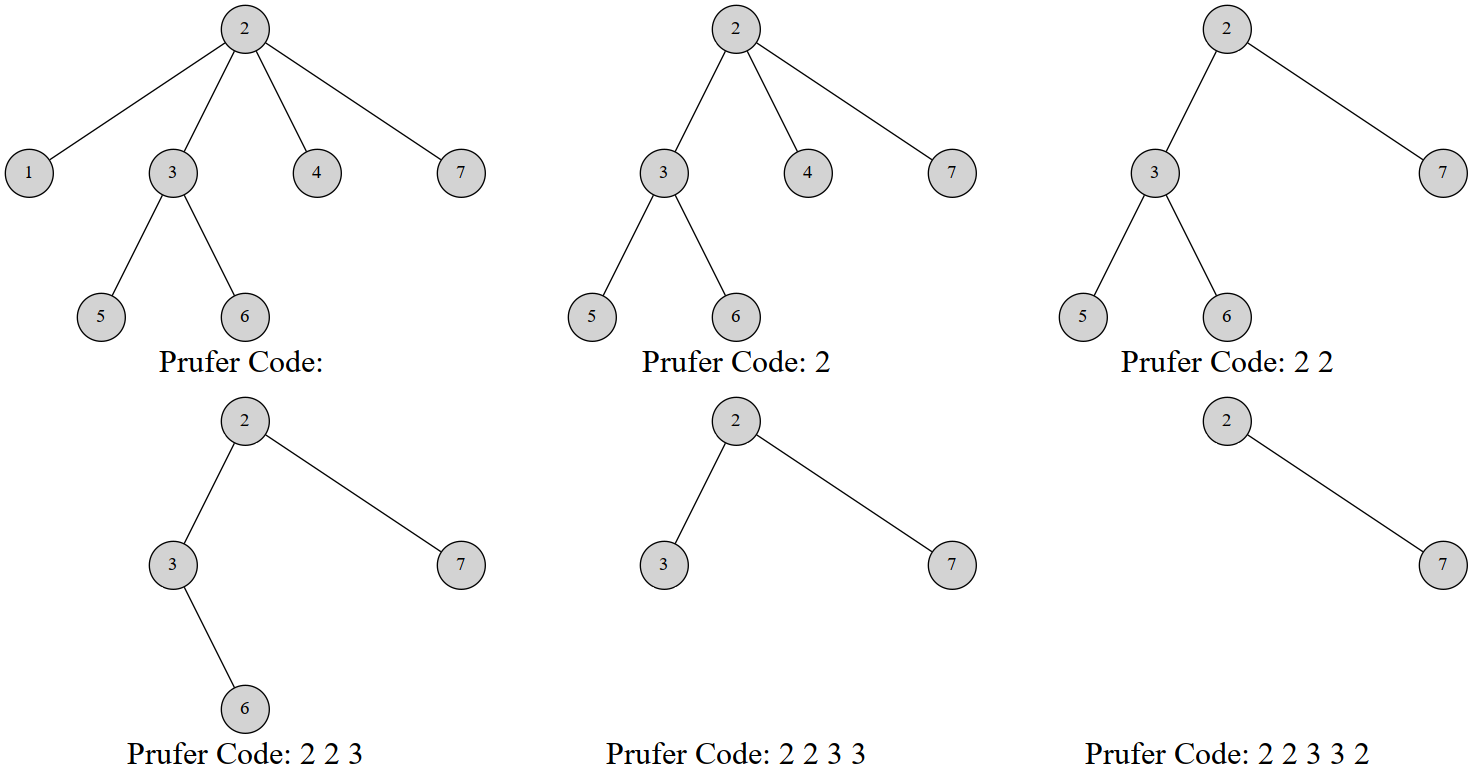
Prüfer 序列是这样建立的：每次选择一个编号最小的叶节点并删掉它，然后在序列中记录它连接到的那个节点，重复 \(n-2\) 次后就只剩下两个节点，就结束了。

给张图（来自 OI Wiki）

用优先队列维护堆显然可以做到 \(O(n\log n)\)。

但也有线性的构造方式。

可以线性构造的原因是叶节点的性质，叶子节点的个数是单调不升的。每次删掉一个叶子节点，要么又新增一个，要么不增。

过程

维护一个指针 \(p\)。初始时指针 \(p\) 指向编号最小的叶节点。同时我们维护每个节点的度数，方便我们知道在删除叶节点的过程中是否产生了新的叶节点。流程如下：

1. 删除 \(p\) 指向的节点，维护度数，检查是否产生新的叶节点。

2. 如果产生新的叶节点，假设编号为 \(x\)，我们比较 \(p,x\) 的大小关系。如果 \(x > p\)，那么不做操作；否则立即删除 \(x\)，然后检查删除 \(x\) 后是否产生新的叶节点，重复步骤 \(2\)，直到未产生新的叶节点或者新节点的编号 \(>p\)。

3. 让指针自增直到遇到一个未被删除叶节点为止。

可以证明，每条边最多被访问一次（在删度数的时候），而指针最多遍历每个节点一次，因此复杂度是 \(O(n)\) 的。

代码来自洛谷模板，在这个题中为了好写是一棵有根树，\(f\) 数组表示的是每个节点的父节点，\(p\) 数组表示的就是 Prüfer 序列。

	for(re int i=1;i<=n-1;i++) f[i] = read() , du[f[i]]++;
	for(re int i=1,j=1;i<=n-2;i++,j++)
	{
		while(du[j]) j++;//找叶子节点
		p[i] = f[j];
	}//所以这个复杂度是 O(n) 的
	for(re int i=1;i<=n-2;i++) ans ^= 1ll * i * p[i];
	cout << ans;

小性质

1. 在构造完 Prüfer 序列后原树中会剩下两个节点，其中一个一定是编号最大的点 \(n\)。

2. 每个节点在序列中出现的次数是其度数减 \(1\)。

根据 Prüfer 序列重建树

重建树的方法也是类似的，通过 Prüfer 序列我们可以得到原树上每个点的度数。然后你也可以得到编号最小的叶节点，而这个叶节点一定与 Prüfer 序列的第一个数连接，然后我们同时删掉这两个点的度数，这就是大致思路。

同理，我们用优先队列维护度数为 \(1\) 的节点的小根堆，同样能做到 \(O(n\log n)\)。

也是同理，这个也有线性做法。

同理，让 \(p\) 指向编号最小的叶子节点，\(i\) 指针指向 Prüfer 序列的第 \(i\) 位。

1. 删除 \(p\) 指向的节点的度数，将它与 Prüfer 序列的第 \(i\) 位相连，同时删除 \(i\) 的度数，检查是否产生新的叶节点。

2. 如果产生新的叶节点，假设编号为 \(x\)，我们比较 \(p,x\) 的大小关系。如果 \(x > p\)，那么不做操作；否则立即删除 \(x\) 的度数，连边，然后检查删除 \(x\) 度数后是否产生新的叶节点，重复步骤 \(2\)，直到未产生新的叶节点或者新节点的编号 \(>p\)。

3. 让指针自增直到遇到一个未被删除叶节点为止。

for(re int i=1;i<=n-2;i++) p[i] = read() , du[p[i]]++;
	p[n-1] = n;
	for(re int i=1,j=1;i<=n-1;i++,j++)
	{
		while(du[j]) j++;
		f[j] = p[i];
		while(i <= n-1 && !(--du[p[i]]) && p[i] < j) f[p[i]] = p[i+1] , i++;
	}
	for(re int i=1;i<=n;i++) ans ^= 1ll * i * f[i];
	cout << ans;

Cayley 公式（Cayley's formula）

对于一棵完全图 \(K_n\) 有 \(n^{n-2}\) 棵生成树。

这个用 Prüfer 序列证明最简单。任意一个长度为 \(n-2\) 的值域为 \([1,n]\) 的整数序列都可以通过 Prüfer 序列双射对应一个生成树，于是方案数就是 \(n^{n-2}\)。

图联通方案数

一个 \(n\) 个点 \(m\) 条边的带标号无向图有 \(k\) 个连通块，我们希望添加 \(k-1\) 条边使得整个图连通。求方案数。

设 \(s_i\) 表示每个连通块的数量，然后最后的答案就是

\[n^{k-2}\cdot \prod_{i=1}^ks_i \]

说实话，OI-Wiki 上的证明没咋看懂，如果想了解可以去OI-Wiki上看一下证明。

给定度数无根树计数

给定每个点的度数，求出有多少符合条件的无根树。

设每个点的度数是 \(d_i\) ，先给出结论：个数 \(=\)

\[\frac{(n-2)!}{\displaystyle \prod_{i=1}^n(d_i-1)!} \]

从 Prüfer 序列的角度来看，由 Prüfer 序列的性质 \(2\)，我们可以知道度数为 \(d_i\) 的点会在 Prüfer 序列中出现 \(d_i-1\) 次，那么这其实就是可重集排列数了，总共 \(n-2\) 个位置，每个 \(d_i\) 会重复 \(d_i-1\) 次，套上可重集排列数的公式，就是答案。

还需要注意一些特判，比如 \(n=1\) 或者 \(\sum d_i \not= 2n-2\) 的情况，后者是铁定无解的，前者要看 \(d_1\)，如果是 \(0\)，答案就是 \(1\)，其余都是 \(0\)。