线性代数相关
矩阵
定义
一个
其余定义
同型矩阵
同型矩阵指的是两个矩阵,如果它们的行数和列数对应相同,那么它们两个就被称为同型矩阵。
方阵
行数等于列数的阵称为方阵。一般所说的「
主对角线
对于方阵
对称矩阵
如果方阵的元素关于主对角线对称,即对于任意的
对角矩阵
主对角线之外的元素均为
其中
很显然,对角矩阵也是对称矩阵。
单位矩阵
如果对角矩阵的元素均为
三角矩阵
如果方阵主对角线左下方的元素均为
运算
加法(减法)
两个矩阵进行加减法运算就是把两个矩阵对应位置上的数相加减,即
引用子谦
大佬的几张图。
数乘
类似于向量,
数乘运算中,类似于向量的,有以下运算律:
转置
矩阵的转置,就是在矩阵的右上角写上转置
对称矩阵转置前后保持不变。
乘法
矩阵乘法只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。
设
其中
也就是说,在矩阵乘法中,结果
矩阵乘法满足以下运算律:
结合律:
矩阵的结合律往往是我们解题的关键。
分配律:
不满足交换律
但有一种特殊情况:
常数优化
因为
矩阵加速递推
前置:矩阵快速幂
矩阵快速幂,顾名思义,就是矩阵套个快速幂。
首先把
时间复杂度
矩阵加速
先来道例题:P1962 斐波那契数列。题意很简单,就是让你求斐波那契数列的第
显然有暴力的
考虑优化。我们知道,
设
那么就有
至此,我们得到了一个矩阵乘法的递推式,我们初始化
适用情况
-
可以抽象出一个长度为
-
变化的形式是一个线性递推(只有若干“加法”,或者“乘一个系数”的运算);
-
该递推式在每个时间可能作用与不同的数据上,但本身保持不变;
-
向量变化时间(即递推轮数)很长,但向量长度
有了这几个特点,我们就可以考虑矩阵乘法优化了。我们把这个长度为
矩阵乘法加速递推的难点就在与构造,构造出一个合适的状态矩阵,再构造出一个合适的转移矩阵,之后就没有难度了,直接套矩阵快速幂即可。时间复杂度是
行列式
符号与定义
其中,
只有方阵才有行列式
基本性质
-
证明:根据定义可知,要使得
-
根据单位矩阵主对角线都是
-
交换排列的两个数会让排列逆序对数量改变奇偶性,因此相当于为每个
-
每个排列里
-
交换这两行会让行列式变号,但是矩阵保持不变,即
-
结合性质
-
设不等的编号为
-
设
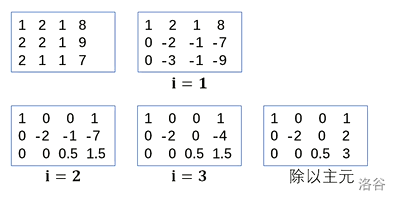
高斯消元
介绍
高斯消元是一种求解线性方程组的方法。所谓线性方程组,是由
高斯消元就是利用该矩阵进行一些操作来进行的。
初等行变换
上述操作可以分为三种。
- 交换两行;
- 把某一行乘一个非
- 把某行的若干倍加到另一行上去。
进行上述操作之后,我们可以知道,方程组的解并不会发生变化。上述三类操作就被称为矩阵的初等行变换。
思路
高斯消元法
高斯消元法的基本思路是利用矩阵的初等行变换将系数矩阵(除最后一列外的地方)消成上三角矩阵,再下到上回代求解。
-
枚举主元(主对角线上的元素),找到主元下面系数不是
-
用变换
-
用变换
-
用变换
解可以有三种情况:
-
唯一解:
-
无解:存在
-
无穷多解:存在
高斯-约旦消元法
与高斯消元法不同的是,高斯-约旦消元法把系数矩阵消成主对角矩阵,这样每一行
每轮循环,主元所在行不变,主元所在列消成
应用-矩阵求逆
对于方阵
我们可以利用高斯消元在
思路
其实比较简单。
-
我们构造
-
用高斯-约旦消元法将其化简为
这个的原理其实挺简单。首先根据定义我们可以比较容易得出一个结论:
如果左边出现了全
代码其实没变多少,这里以模板题为例,模板题是模意义的高斯消元,所以有些地方加上了快速幂来求逆元。
应用-行列式求值
按照定义计算行列式是
由性质
根据性质
代码也是模板题的,这个模板题模数非质数,需要用到辗转相除的思想,复杂度均摊
Matrix-tree 定理
写的会比较简略,因为证明不是很会。
前置:高斯消元求行列式。
Matrix-Tree 定理,顾名思义,它阐明了矩阵和生成树之间的关系,它要用到的矩阵叫基尔霍夫(Kirchhoff)矩阵,我们来说一下它怎么求得。
内容
首先我们给出 Matrix-Tree 定理的内容:
基尔霍夫矩阵的任意一个代数余子式的值,就是所有生成树的边权积的和。
当边权为
其中代数余子式的简略定义就是一个
此定理对于有向图和无向图之间还有一些区别,下面我们分别讨论一下。
设
无向图
其实无向图才是 Matrix-Tree 最本质的内容,有向图其实是一个扩展。
假设给定一个图
度数矩阵
邻接矩阵
基尔霍夫矩阵的定义是度数矩阵减去邻接矩阵,即
我们删去任意一行和任意一列,求剩下的矩阵的行列式即可。
有向图
假设给定一个图
度数矩阵
邻接矩阵
基尔霍夫矩阵即
我们删去指定的根所在的行和列,求剩下的矩阵的行列式即可。
简式
其实 Matrix-Tree 定理用数学语言来写的话,它求的就是
其中
例题
以模板题为例,给出无环图生成树和有环图外向树的代码,模板题中以
这个题就运用到了我前面所说的简式
这个题因为还要保证只有
此时就有一步比较巧妙的转化:
那么式子就转化成了
我们发现最后那个连乘其实是一个常数,我们把它提到外面去
我们以右边的分式作为
发现我是个神必..其实这个建图很好建立,相邻的 . 连边就行了。但是需要注意的是,矩阵树定理是给出一个连通图求生成树个数的,你如果图都不连通你求啥生成树啊。
就是说我们需要保留有用的状态,题目中的柱子就是无用状态,你不能把它放到矩阵中,因为这样一定会出现对角线为
容斥 + Matrix-Tree。
如果在求行列式的过程中考虑不同公司的贡献的话是比较难的,这就指引我们要在求生成树的过程前把这种贡献表示出来,这就又提醒我们可以用容斥。我们枚举子集,表示哪几个公司上去修路。设
我们
BEST 定理
设
其中
用的很少,提一嘴就行了。
线性空间
矩阵的加法和数乘运算所具有的不少性质,是一般线性空间同样具有的,事实上线性空间的定义本身就是从矩阵(以及其它一些数学对象)所具有的运算性质中抽象出来的。”
定义
线性空间
线性空间是一个关于以下两个运算封闭的向量集合。
-
向量加法
而加法要满足这么几个性质:
(1)
(2)
(3) 线性空间中有这么一个
(4) 对于向量
-
标量乘法
而数乘需要满足这么几个性质:
(1)
(2)
(3)
(4)
满足这两个大条件,就说这是一个线性空间。我们由此可以知道,这里的加法和乘法是广义的加法和乘法,也就是只要满足这几个条件,就能把它称之为加法和乘法,类似于 C++ 里面的运算符重载。
生成子集
给定若干个向量
线性相关和线性无关
任意选出线性空间内的若干个向量,如果其中存在一个向量能被其他向量表出,则称这些向量线性相关,否则称这些向量线性无关。
基和维数
线性无关的生成子集被称为线性空间的基底,简称基。基的另一种定义是线性空间的极大线性无关子集。一个线性空间内的所有基包含的向量个数一定都相等,这个个数被称为线性空间的维数。
以平面直角坐标系为例。平面直角坐标系中的所有向量构成一个二维线性空间,它的一个基就是单位向量集合
矩阵的秩
对于一个
把这个
为零的行向量因为可以由其它非零行向量
线性基
前置知识:上文提到的线性空间的一些内容。
下文只讨论异或空间的线性基,如果是实数空间,高斯消元是求实数空间的线性基的好方法。
类似于上文线性空间的一些定义,我们简单定义一下异或空间的一些定义。
参考文章:
-
《算法竞赛进阶指南》-李煜东
定义
异或和
设
生成子集与张成
若整数
这个构成的异或空间称为集合
线性相关与线性无关
任意选出异或空间中的若干个整数,如果存在一个整数能被其他整数表出,则称这些整数线性相关,否则称这些整数线性无关。异或空间的基就是异或空间中一个线性无关的生成子集,或者定义为异或空间的极大线性无关子集。
线性基
其实上面已经给出了,我们详细地给它定义一下。
若称集合
-
-
集合
线性基有一下基本性质:
-
-
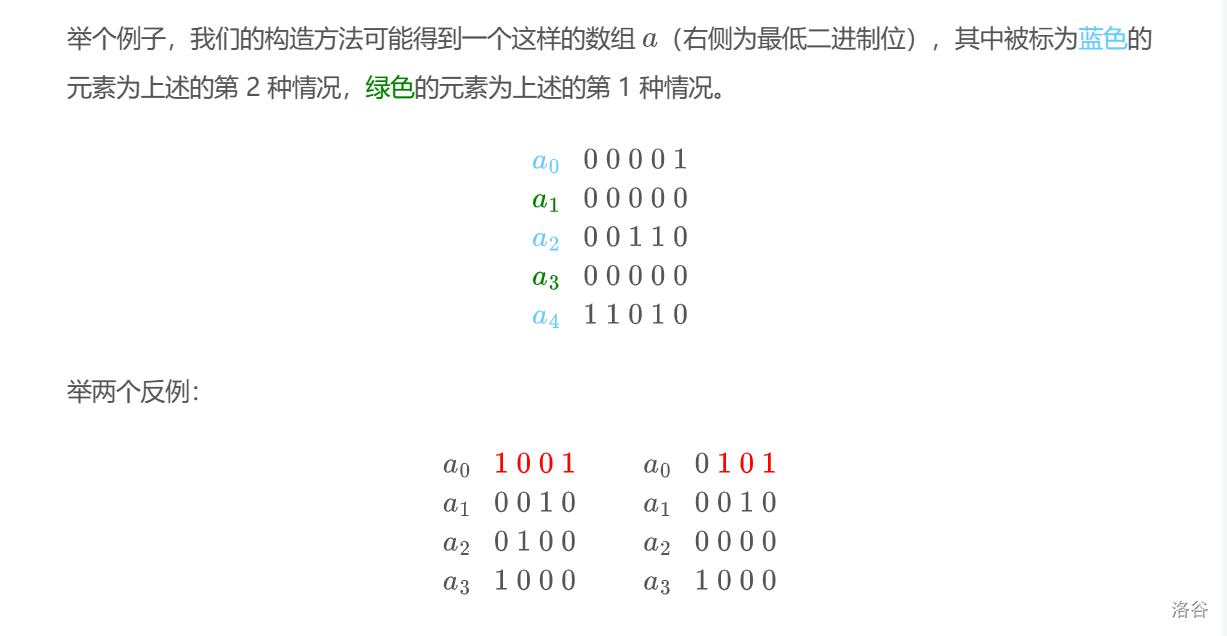
构造与性质
这种构造学的 Menci,它的原理其实是高斯消元,这玩意只可意会不可言传,看多了其实你能感觉到它和高斯消元的相同之处。
设集合
这种线性基的构造方法保证了一个特殊性质,对于每一个
- 只有满足
-
整个
-
-
我们称第
这其实就相当于第
Menci 的博客里给出了例子,我不要脸的引用一下/cy。
知道了性质以后,我们根据性质来构造线性基。
首先,线性基是动态构造的,你给定不同的数它就可能构造出不同的线性基,这比较显然。我们从空的
从
-
-
-
-
-
流程
我们再来简易地捋一遍这个流程
从高位到低位枚举
-
如果
-
如果
-
枚举
-
枚举
-
令
-
给出代码
证明
我们枚举
我们想一想它的插入过程,我们每次找到
可以看出,一次插入的复杂度为
应用
学会构造以后,我们看一下它的一些应用。
合并线性基
这个其实不算应用,就是把两个集合的线性基在
这其实也很简单,把一个线性基中的所有元素插入到另一个线性基中即可。
判断
这个的原理和构造的原理类似,如果
异或最大值
给定一个集合
这种构造方法的好处之一就体现在这里。从高到低考虑在线性基中的二进制位
异或和最小值
有异或最大值,就有异或最小值。
这里我之前在构造线性基里提到的 flag = 1 就有作用了。如果说我们插入了一个数
如果
第
这种构造方式的第二个优点体现在这里。
首先我们求出集合的线性基 flag=1 的时候,会有
若
否则,将
-
高位上的
-
不论哪一位,如果这一位是
而线性基的
与从线性基中选数相对应:
-
选择「控制较高位上的
-
不论哪一位,如果选择了哪一位「控制
根据这个性质,解法就出来了:枚举
后记
当然线性基的应用远不止于此,还有线性基求交,待删除线性基等一些科技,鉴于我现在的能力范围还达不到,故略去。
总·后记
OI 中有关线性代数的部分明面上就这么多,当然还是鉴于能力范围,一些更深入层次上的部分我还没有涉及。还是那句话,如果你想学数学,在有时间的情况下建议还是看书,成体系的知识往往比零碎的好。但可惜我没有那么多的时间,因此只能自己整理一下可能用到的内容。也希望这篇博客对读者能够有所帮助。

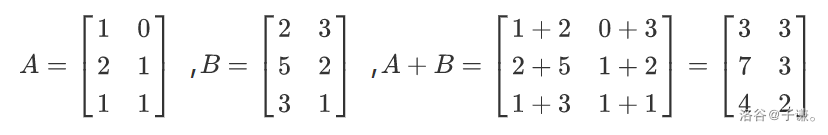
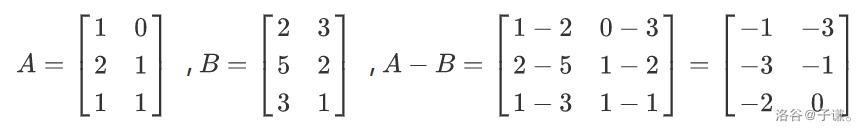
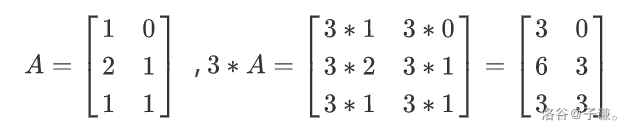
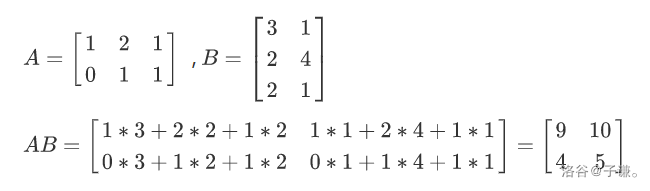




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 清华大学推出第四讲使用 DeepSeek + DeepResearch 让科研像聊天一样简单!
· 推荐几款开源且免费的 .NET MAUI 组件库
· 实操Deepseek接入个人知识库
· 易语言 —— 开山篇
· Trae初体验