动态规划 - 石子合并问题
(1)问题描述
在一个圆形操场的四周摆放着 num 堆石子。先要将石子有次序地合并成一堆。规定每次只能选相邻的 2 堆石子合并成新的一堆,并将新的一堆石子数记为该次合并的耗费力气。试设计一个算法,计算将 n 堆石子合并成一堆的最省力气数。
(2)算法思想
对于给定的 n 堆石子,当只有一堆时,不用搬,进而不耗费力气,然后依次计算出从 2 堆 ~ num 堆石子的最优解,并且堆数递增求最优解,依赖于上一步的解进行计算所得;
(3)算法思路
此解法和矩阵连乘类似,我们知道矩阵连乘也是每次合并相邻的两个矩阵,那么石子合并可以用矩阵连乘的方式来解决。
设 dp[i][j] 表示第 i 到第 j 堆石子合并的最优值,sum[i][j] 表示第 i 到第 j 堆石子的所耗费的力气总数。动规方程如下:
(4)代码展示

public class StoneMerge { /** * 记录石子堆的数量 */ private static int num; /** * 记录每堆石子的重量 */ private static int[] weight; /** * 记录石子堆断开的位置【便于计算局部最优解】 */ private static int[][] location; /** * 记录石子堆局部最优解,以至于求得最终最优解【动规方程】 */ private static int[][] dp; /** * 初始化数据 */ private static void initData() { Scanner input = new Scanner(System.in); System.out.println("请输入石子堆数量:"); num = input.nextInt(); weight = new int[num]; System.out.println("请输入每堆石子的重量:"); for (int i = 0; i < weight.length; i++) { weight[i] = input.nextInt(); } // 定义成 int 类型的二维数组,创建完每个元素直接初始化为 0 dp = new int[num][num]; location = new int[num][num]; } /** * 计算最省最费力气值 */ private static void dpFindMinStrength() { // 初始化 dp 数组 for (int m = 0; m < num; m++) { dp[m][m] = 0; // 一堆石子,不用搬,耗费力气为 0 } for (int r = 2; r <= num; r++) { // 从 2 堆依次到 num 堆,分别计算最优值 for (int i = 0; i < num - r + 1; i++) { // 起始石子堆取值范围 int j = i + r - 1; // 根据每次选取石子堆 r 和起始石子堆 i ,计算终止石子堆 int sum = 0; for (int x = i; x <= j; x++) { // 计算从石子堆 i 到 石子堆 j 合并时,最后两堆使用的力气总和 sum sum += weight[x]; } // 根据动规方程,从局部最优解中计算当前从石子堆 i 到石子堆 j 合并所使用的的力气总和 dp[i][j] = dp[i + 1][j] + sum; // 计算从 i 石子堆分开时,使用的力气总和 location[i][j] = i; // 标记从第 i 石子堆分开位置 for (int k = i + 1; k < j; k++) { // 需要统计从 k 【k ∈ (i, j)】石子堆分开,使用的力气总和 int temp = dp[i][k] + dp[k + 1][j] + sum; // 计算从 k 石子堆分开时,使用的力气总和 if (temp < dp[i][j]) { dp[i][j] = temp; location[i][j] = k; } } } } } /** * 输出 */ private static void print() { System.out.println("动规数组【不同堆数合并石子所费力气】:"); for (int i = 0; i < num; i++) { for (int j = 0; j < num; j++) { System.out.print(dp[i][j] + " "); } System.out.println(); } System.out.println("不同堆数合并石子最省力气断开位置最优解:"); for (int i = 0; i < num; i++) { for (int j = 0; j < num; j++) { System.out.print(location[i][j] + " "); } System.out.println(); } } public static void main(String[] args) { // 初始化数据 initData(); // 计算最省最费力气值 dpFindMinStrength(); // 输出 print(); } }
(5)输入输出

请输入石子堆数量: 4 请输入每堆石子的重量: 4 4 5 9 动规数组【不同堆数合并石子所费力气】: 0 8 21 43 0 0 9 27 0 0 0 14 0 0 0 0 不同堆数合并石子最省力气分开位置最优解【下标从数组 0 开始分开】: 0 0 1 2 0 0 1 2 0 0 0 2 0 0 0 0
(6)总结
石子合并问题完全提现了动态规划的核心思想,先求解子问题的解【子问题求解不相互独立,相互依赖】,然后从这些子问题的解中得到原问题的解,进而得到该问题的最优解。


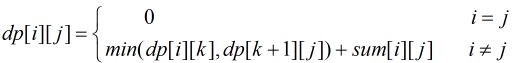


 浙公网安备 33010602011771号
浙公网安备 33010602011771号