回溯算法 - 全排列

（1）问题描述：对于给定的集合 A{a1,a2,...,an}，其中的 n 个元素互不相同，如何输出这 n 个元素的所有排列（全排列），时间复杂度为O(2ⁿ)；

　　例如：{a, b, c}

　　全排列：{a, b, c}, {a, c, b}, {b, a, c}, {b, c, a}, {c, a, b}, {c, b, a}

（2）回溯算法思想：

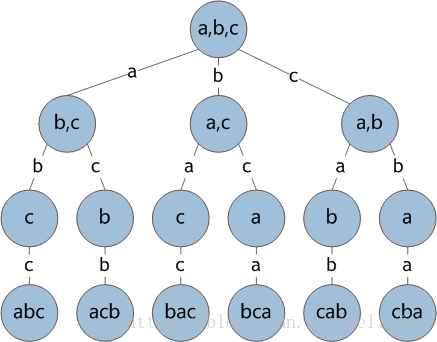
　　这里以 A{a, b, c} 为例，来说明全排列的生成方法，对于这个集合，其包含 3 个元素，所有的排列情况有 3!=6 种，对于每一种排列，其第一个元素有 3 种选择 a, b, c，对于第一个元素为 a的排列，其第二个元素有 2 种选择 b, c；第一个元素为 b 的排列，第二个元素也有2种选择a，c，……，依次类推，我们可以将集合的全排列与一棵多叉树对应。如下图所示：

　　

（3）算法代码：

public class FullPermutation {

    /**
     * 存放数据数组
     */
    private static Integer[] data;

    /**
     * 数据数量
     */
    private static Integer num;

    /**
     * 交换数据
     */
    public static void swap(int x, int y) {
        Integer temp = data[x];
        data[x] = data[y];
        data[y] = temp;
    }

    /**
     * 初始化数据
     */
    private static void initData() {
        Scanner input = new Scanner(System.in);
        System.out.println("请输入数据数量:");
        num = input.nextInt();
        System.out.println("请输入数组数据");
        data = new Integer[num];
        for (int i = 0; i < data.length; i++) {
            data[i] = input.nextInt();
        }
    }

    /**
     * 递归回溯排列树求解
     */
    private static void backtrack(int t) {
        if (t == data.length) {
            System.out.print("排列树为: ");
            Stream.of(data).forEach(element -> System.out.print(element + " "));
            System.out.println();
        }
        for (int i = t; i < data.length; i++) {
            swap(t, i);
            backtrack(t + 1);
            swap(t, i);
        }

    }


    public static void main(String[] args) {
        // 初始化数据
        initData();

        // 递归回溯排列树求解
        backtrack(0);
    }

}

（4）输入输出

请输入数据数量:
4
请输入数组数据
1 2 3 4
排列数为: 1 1 2 3 
排列数为: 1 1 3 2 
排列数为: 1 2 1 3 
排列数为: 1 2 3 1 
排列数为: 1 3 2 1 
排列数为: 1 3 1 2 
排列数为: 1 1 2 3 
排列数为: 1 1 3 2 
排列数为: 1 2 1 3 
排列数为: 1 2 3 1 
排列数为: 1 3 2 1 
排列数为: 1 3 1 2 
排列数为: 2 1 1 3 
排列数为: 2 1 3 1 
排列数为: 2 1 1 3 
排列数为: 2 1 3 1 
排列数为: 2 3 1 1 
排列数为: 2 3 1 1 
排列数为: 3 1 2 1 
排列数为: 3 1 1 2 
排列数为: 3 2 1 1 
排列数为: 3 2 1 1 
排列数为: 3 1 2 1 
排列数为: 3 1 1 2 

（5）总结：回溯算法是有一定的规律可循的，根据问题，找出解空间的组织结构，选择恰当的解决方案：回溯算法模板。

　　回溯算法一般采用深度优先的方式，递归求解，人的思维一般对递归求解的问题有一定的想象难度，建议在纸上根据代码的流程，画一画走一遍详细的过程，便于理解回溯算法的核心要点。