知识梳理:递归和回溯
递归
递归的定义:一个函数function直接或者间接调用自身,则该函数称为递归函数。
递归函数有两个重要的概念:
- 递推关系:一个问题的结果与其子问题的结果之间的关系。
- 基本条件:跳出递归调用的条件。
当我们找到这两个要点时,就可以实现一个递归函数了,只需用递推关系调用函数,直到基本条件跳出递归。
注意:如果递推关系和基本条件 不正确,递归很容易进入死循环。
递推关系
推导出递推关系,那么递归函数就成功了80%。下面用一个累加的简单例子做说明:
1+2+3+4+...+n
可以很容易的看出,第n个的总值 = 第n-1的总值 + n的值。
所以递推关系就是f(n)=f(n-1)+n。f(n) 每次执行时依赖 f(n−1)f(n-1)f(n−1) 的结果,所以我们把 f(n−1)f(n-1)f(n−1) 的结果看作是中间变量。
递归分类
递归可以分为两种形式:由下到上和由上到下。
由下到上
在每个递归层次上,我们首先递归地调用自身,然后根据返回值进行计算。(依赖返回值)
流程如下:
- 寻找递归基本情况
- 寻找递归递推关系
- 修改递归函数的参数
- 递归调用并返回中间变量
- 使用递归函数的返回值与当前参数进行计算,并返回最终结果
还是拿上面的累加的例子作说明:
function sum(n){
if(n==1) return n;
let prev = sum(n-1);
return prev+n;
}
由上到下
如果我们把上面第四步返回的中间变量抽取出来,并在递归调用函数时当成参数传给自身,这就是由上到下的递归。
流程如下:
- 寻找递归基本情况
- 寻找递归递推关系
- 把中间变量改成函数参数
- 根据函数参数与中间变量重新计算出新的中间变量
- 修改参数
- 递归调用并返回
function sum(n,total){
if(n==1) return n;
total += n;
return sum(n-1,total);
}
区别:两者的主要区别在于于对中间变量的处理,参与计算的中间变量是参数提供的还是返回值提供的。
回溯
定义: 回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。(百度百科)
回溯算法需要了解下面3个概念:
- 路径:也就是已经做出的选择
- 选择列表:也就是你当前可以做的选择
- 结束条件:也就是到达决策树底层,无法再做选择的条件
伪代码如下:
let rs = [];
function backtrack(路径,选择列表){
if(满足结束条件) return rs.push(路径);
for(选择 in 选择列表){
做选择
backtrack(路径,选择列表);
撤销选择
}
}
核心代码是在循环选择列表里面,在递归前先做出‘选择’,然后在递归后‘撤销选择’。
下面以全排列作为例子。如何用回溯拿到所有的排列组合呢,看下面的图理解上面说说的3个概念。

由上图可知:从1->2的过程就是已经选择的路径; 以节点1()为例,它的当前可选择列表就是它的子节点(2,3),那结束条件就是到达树的底层了。
好,既然这3个关键点都找出了了,就可以按照伪代码中的套路写回溯算法了。代码如下:
const Backtrack = (input)=>{
const backtrack = (input,temp)=>{
if(temp.length === input.length)
return rs.push(temp.slice());
// 这里要用slice返回一个新的数组,道理相信大家都明白
for(let i=0;i<input.length;i++){
if(temp.includes(input[i])) continue;
temp.push(input[i]); // 做出选择
backtrack(input,temp);// 调用递归
temp.pop();// 撤销选择
}
}
}
详细的步骤可以看下面的流程图:
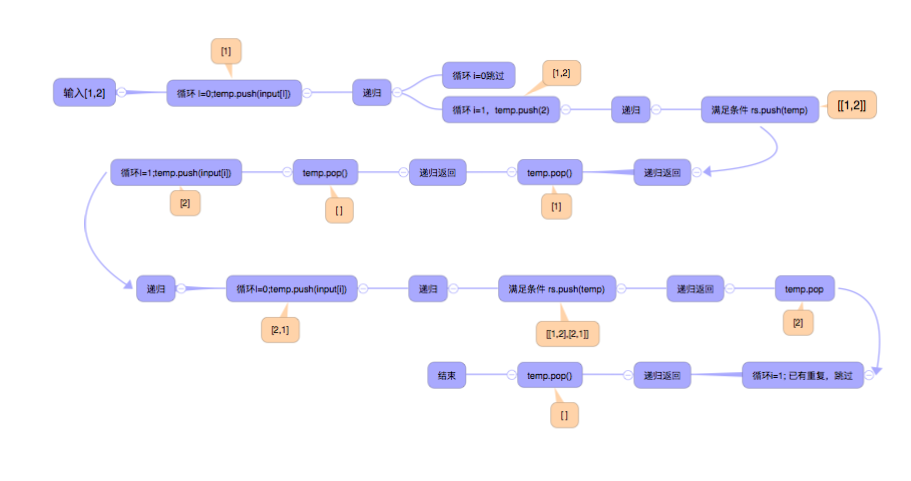
其实回溯算法就是纯暴力穷举,无论怎么优化,复杂度还是很高,因为它无法避免穷举整棵决策树。




