程序员面试金典：面试题 01.07. 旋转矩阵

给你一幅由 N × N 矩阵表示的图像，其中每个像素的大小为 4 字节。请你设计一种算法，将图像旋转 90 度。
不占用额外内存空间能否做到？

//使用了额外内存空间
class Solution {
    public void rotate(int[][] matrix) {
        int m = matrix.length;
        int[][] copyMatrix = new int[m][m];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < m; j++) {
                copyMatrix[i][j] = matrix[m - 1 - j][i];
            }
        }
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < m; j++) {
                matrix[i][j] = copyMatrix[i][j];
            }
        }
    }
}

进阶：不使用额外空间
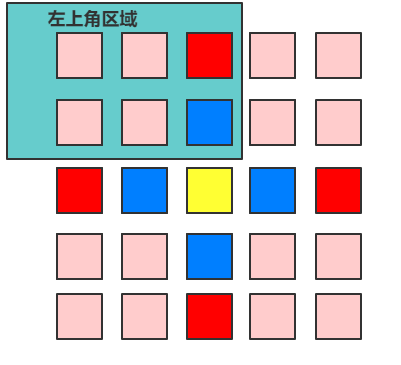
观察图中颜色相同的四个位置，当旋转 90 度后，对应位置的元素发生了顺时针的交换。

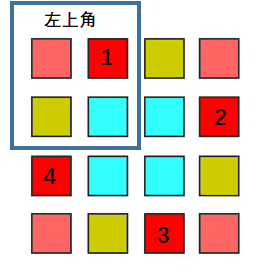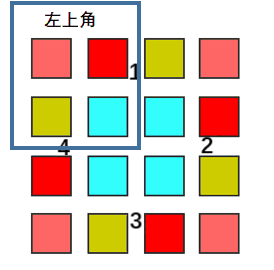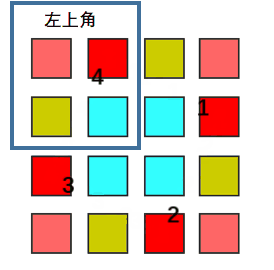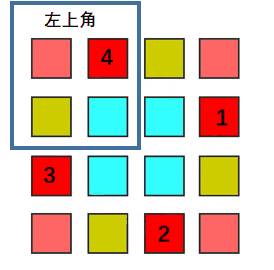
而相隔的两个位置是中心对称的，基于此可以计算出发生交换的四个元素 位置关系。
设四个位置中，位于 左上角区域 的位置坐标为 (i,j)，则按顺时针顺序，四个位置分别为(i,j), (j, n-i-1), (n-i-1,n-j-1), (n-j-1,i)。其中 n 为 matrix.size(), i, j 分别为matrix的行列下标，从 0 开始。
整个矩阵的旋转可以理解为 起点都在左上角区域，然后依次顺时针移动。
matrix.size() 为奇数时，位置的对应关系相同，但左上角区域并 不是整个矩阵的四分之一，如下图示：

其实就是多了中间列的上半部分。

那么现在捋一下如何 原地操作元素：枚举左上区域的所有位置，然后通过上面总结的位置关系直接交换元素。
对于一个位置 (i,j)，需要 交换三次：

swap(matrix, i, j, j, n - 1 - i);
swap(matrix, i, j, n - 1 - i, n - 1 - j);
swap(matrix, i, j, n - 1 - j, i);

整体代码如下：

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        if (n == 0) {
            return;
        }
        int row = n / 2 - 1;//左上角区域最下面一行
        int column = (n - 1) / 2;//左上角区域最右面一列
        for (int i = 0; i <= row; i++) {//数学知识，两两中心对称
            for (int j = 0; j <= column; j++) {
                swap(matrix, i, j, j, n - 1 - i);
                swap(matrix, i, j, n - 1 - i, n - 1 - j);
                swap(matrix, i, j, n - 1 - j, i);
            }
        }
    }
    private void swap(int[][] matrix, int i, int j, int m, int n) {
        int temp = matrix[i][j];
        matrix[i][j] = matrix[m][n];
        matrix[m][n] = temp;
    }
}