《基于统计模型的高考志愿填报决策分析》论文笔记(十九)
一、基本信息
标题:基于统计模型的高考志愿填报决策分析
时间:2014
二、研究内容
1.主要内容
文章基于传统志愿和平行志愿录取机制,依据考生填报志愿的真实偏好和考生分数名次号,分别建立了传统志愿填报概率模型和平行志愿填报概率模型,考生在信息不完全掌握的情况下,计算出被高等学校录取的概率,提高考生志愿填报的有效性和高考录取的可能性。与传统志愿填报模式相比,平行志愿模式增加了被投档的机会和录取几率、提高了考生报考志愿的满意度。
2.高考录取问题的基本假设
假设某省(市)共有N个考生符合条件填报高考志愿,有L所高校可供选择,定义:S={s1....sn},N个考生的集合;F={ f1....fn},每位考生对应名次号集合; C={ c1....cn},考生所在省(市)招生的高校集合;Q = { q1....qn},每所高校对应的计划招生数集合;P = { p1....pn},考生对学校偏好集合。考生si在填报志愿时,高考录取问题五元集{S,F,C,Q,P} 中的 {S,F,C,Q,} 为充分信息,而对于其他考生偏好 pj和相关志愿填报因属于私人信息而难以掌握,因此 P ={p1....pn }具有不完全信息特征。对于任意符合投档条件的考生 si,存在若干 c i属于C,假设考生选择不上大学或出国留学,则不偏好于任何一所学校,此时ci= c0,c0表示非国内招生高校。招生单位无论选择哪种录取模式,均会涉及到考生排序问题,高考总分仅有数百分,而考生人数为几十万人,很容易造成同分现象。
3.传统志愿模式的录取机制
(1)传统志愿录取机制模型
传统志愿投档模式的录取机制与“波士顿机制”非常相似,均为“第一志愿优先”原则。传统志愿投档模式只有在第一志愿未录取满的情况下才招收第二志愿的考生,如果当考生未能被第一志愿录取时,往往其所填的第二、第三志愿学校已在第一轮招生中录满,即使他的高考分数高于该学校的录取分数线,考生也只能补报志愿或落到下一批次中录取,个别考生或存在高分落榜的可能性。
(2)传统志愿填报概率模型
考生在填报高考志愿时,对近几年录取分数线波动较大的学校,应考虑“大小年”和“三角年”现象,关注可能填报的学校近四年的最低录取分数线对应的名次号和近四年平均录取分数线对应的名次号。
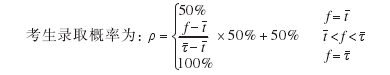
(3)传统志愿模式填报建议
对于传统志愿录取模式,第一志愿被录取的概率大小至关重要。如果录取概率太小,则会出现例1中 s2情况导致高分落榜;如果所填志愿过于保守,可能会出现 s5的高分低录情形,考生未能考上理想的院校。考生在填报志愿时,应对几所准备报考的院校计算出被各校录取的概率,当投档概率小于 50%时,因滑档风险较大而不予考虑,建议考生第一志愿报考录取概率在50%以上的学校,其后的志愿按覆盖率递减原则填报。
4.平行志愿投档模式
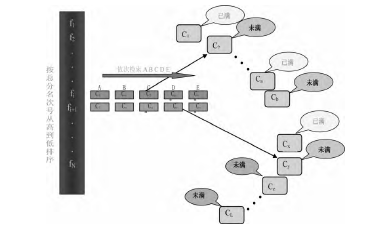
三、结论
通过对本篇期刊的阅读。了解到本文以平行志愿模式,增加了被投档的机会和录取几率、提高了考生志愿的满意率,但仍然存在高分落档的风险。本文分析了两种不同投档模式的高考录取问题,针对考生在信息不完全掌握的情况下,根据考生填报志愿的真实偏好和考生分数名次号计算出被录取的概率,提高考生志愿填报的有效性和高考录取的可能性。
四、参考文献
[1]沈小娟、孙绍荣.基于统计模型的高考志愿填报决策分析[J].上海理工大学管理学院、上海理工大学高等教育研究所,2014.





