决策树

概论

决策树学习通常包括3个步骤：特征选择、决策树的生成和决策树的修剪
决策树由结点和有向边组成。结点有两种类型:内部结点和叶结点，内部结点表示特征，叶节点表示类。
用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点;这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直到达到叶节点。最后将实例分到叶结点的类中。
可以将决策树看成一个if-then规则的集合，将决策树转换成if-then规则的过程是这样的：由决策树的根结点到叶结点的每一条路径构建一条规则；路径上内部结点的特征对应着规则的条件，而叶结点的类对应着规则的结论。 决策树的路径或其对应的if-then规则集合具有一个重要的性质：互斥并且完备。即，每一个实例都被有且仅有一条路径或规则所覆盖。
决策树学习本质上是从训练数据集中归纳出一组分类规则。我们需要的是一个与训练数据矛盾较小的决策树，同时具有很好的泛化能力。
决策树的生成对应于模型的局部选择，决策树的剪枝对应于模型的全局选择。决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。

特征选择

特征选择是决定用哪个特征来划分特征空间
通常特征选择的准则是信息增益或信息增益比
对于数值属性,对训练数据进行排序,假设有k个不同的值,则有K-1个划分,得到k-1个熵,选择最大的作为划分.变为离散属性,即>x,和< x

决策树
贪心算法,只关注当前最大特征,并未从全局考虑(组合数太大,\(2^{2^k}\))
熵越低即越接近0,特征越优
信息增益:分裂前的熵减去分裂后的熵,即用某个属性进行分裂后减少的熵
\(Gini = 1-\sum_{i=0}^{n}[p(i|t)]^2\)
Gini越接近0，特征越优

信息增益

熵：表示随机变量不确定性的度量，设X是一个取有限个值的离散随机变量，其概论分布为\(P(X=x_i)=p_i,\quad i=1,2,\cdots,n\)
则随机变量X的熵定义为：\(H(X)=-\sum_{i=1}^n p_ilogp_i\),由定义可知，熵只依赖于X的分布，而与X的取值无关，所以也可以将X的熵记作\(H(p),H(p)=-\sum_{i=1}^n p_ilogp_i\),熵越大，随机变量的不确定性就越大，从定义可验证\(0 \leq H(p) \leq logn\)
X的分布越均匀，H(p)越大，我们要找的是那些熵H(p)小的特征
条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。定义为X给定条件下Y的条件概率分布的熵对X的数学期望

\[H(Y|X) = \sum_{i=1}^n P(X=x_i)H(Y|X=x_i) \]

信息增益表示得到特征X的信息而使得类Y的信息的不确定性减少的程度,信息增益大的特征具有更强的分类能力。
特征A对顺利数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差，即

\[g(D,A) = H(D)-H(D|A) \]

一般地，熵H(Y)与条件熵H(Y|X)之差称为互信息。决策树学习中的信息增益等价于训练数据集中类与特征的互信息。
根据信息增益准则的特征选择方法是:对训练数据集D，计算其每个特征的信息增益，并比较它们的大小，选择信息增益最大的特征，即\(H(D|A_i)最小的\)。
\(设训练数据集D，|D|表示其样本容量，设有K个类C_k,\)
信息增益算法：
1)计算数据集D的经验熵H(D)

\[H(D)=-\sum_{k=1}^K \frac{|C_k|}{|D|} log \frac{|C_k|}{|D|} \]

2)计算特征A对数据D的经验条件熵H(D|A)

\[H(D|A)=\sum_{i=1}^n\frac{|D_i|}{D}H(D_i)=-\sum_{i=1}^n\frac{|D_i|}{D}\sum_{k=1}^K\frac{|D_{ik}|}{D_i}log\frac{|D_{ik}|}{|D_i|} \]

条件熵H(D|A)是子属性熵\(H(D_i)\)的加权平均
3)计算信息增益

\[g(D,A) = H(D)-H(D|A) \]

信息增益比能解决student ID导致的信息增益最大,student ID熵为0,此时student ID属性的信息增益大,经验熵H(D)也很大.导致信息增益比小于其他属性的信息增益比
\(g_R(D,A)=\frac{g(D,A)}{H(D)}\)

对于标称属性的划分(某个属性有多个值，如车型包括，家用，运动，豪华三个不同的值)
划分方法有两种，二元划分或多路划分。
二元划分顾名思义即进行二元分组，如{运动}和{家用，豪华}，多路划分则是划分成多元分组。随着划分数越大，熵越小，所以信息增益是存在缺陷的。

连续属性负划分
对数值进行排序，得到k个不同的值，对这个k个值取虚拟中点得到K-1个二元分组，评估这k-1个二元分组的熵，得到最优二元划分

决策树的生成

C3算法是用信息增益来选择特征，而C4.5则用信息增益比选择

决策树的剪枝

剪枝从已生成的树上裁掉一些子树或叶结点，并将其根结点或父结点作为新的叶结点，从而简化分类树模型。决策树的剪枝往往通过极小化决策树整体的损失函数来实现。设树T的叶结点个数为|T|,t是树T的叶结点，该叶结点有\(N_t个样本点，其中k类的样本点由N_{tk}个,H_t(T)为叶结点t上的经验熵,a\geq 0为参数，则决策树学习的损失函数可以定义为\)

\[C_a(T) = \sum_{t=1}^{|T|}N_tH_t(T)+\alpha |T|=C(T)+\alpha |T| \]

其中经验熵为\(H_t(T) = -\sum_k\frac{N_{tk}}{N_t}log\frac{N_{tk}}{N_t}\)
C(T)表示模型对训练数据的预测误差，即模型与训练数据的拟合程度，|T|表示模型复杂度，参数\(\alpha\)控制两者之间的影响。而剪枝，就是当\(\alpha\)确定时，选择损失函数最小的子树。

CART

分类树用基尼指数选择最优特征，同时决定改特征的最优二值切分点
分类问题中，假设有K个类，样本点属于第k类的概率为\(p_k\),则概率分布的基尼指数为：

\[Gini(p)=\sum_{k=1}^Kp_k(1-p_k)=1-\sum_{k=1}^Kp_k^2 \]

对于给定的样本集合D，其基尼指数为

\[Gini(D) = 1-\sum_{k=1}^K(frac{|C_k|}{|D|})^2 \]

如果样本集合D根据特征A是否取某一可能值a被分割成\(D_1和D_2\)两部分，则在特征A的条件下，集合D的基尼指数定义为

\[Gini(D,A)=\frac{|D_1|}{|D|}Gini(D_1)+\frac{|D_2|}{|D|}Gini(D_2) \]

基尼指数Gini(D)表示集合D的不确定性，基尼指数Gini(D,A)表示经A=a分割后集合D的不确定性，基尼指数值越大，样本集合的不确定性也就越大，这一点与熵相似。

CART

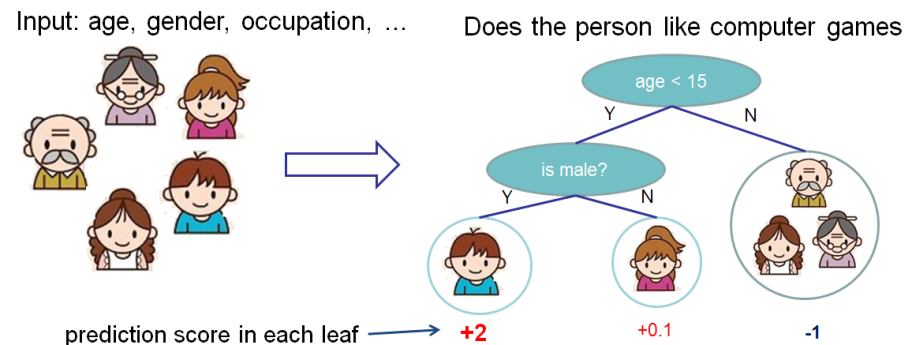
Tree ensembles

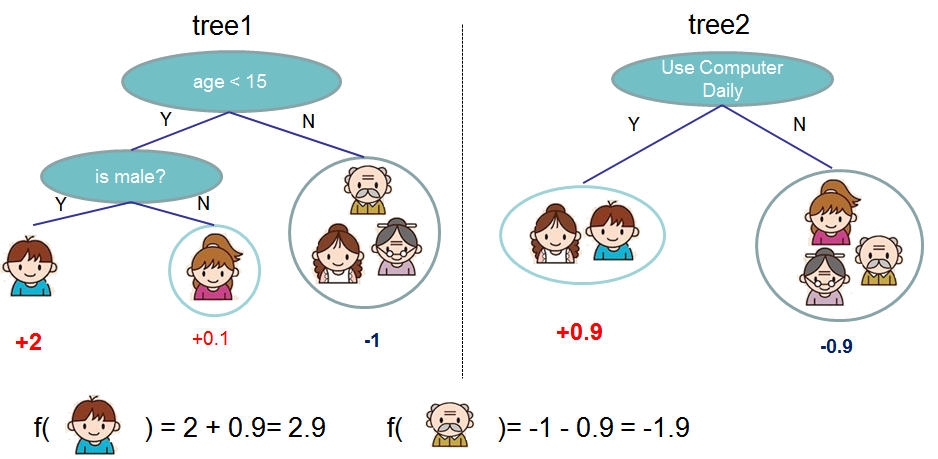
例子:https://wenku.baidu.com/view/87bab95da5e9856a57126005.html