电感的设计
电流纹波定义
定义：电感电流交流量与直流量的比值
电流纹波率也可以用单位电感伏秒积的形式给出
Et是电感的伏微秒积
电流纹波率仅适用于连续导通模式，r的有效值取值范围为0-2，r=0，即纹波为0，那么L需要取∞，显然这种情况只存在于理想状态；r=2，即电感工作在临界导通模式，所谓临界导通模式，定义为Iac = Idc，可见下图这两种情况
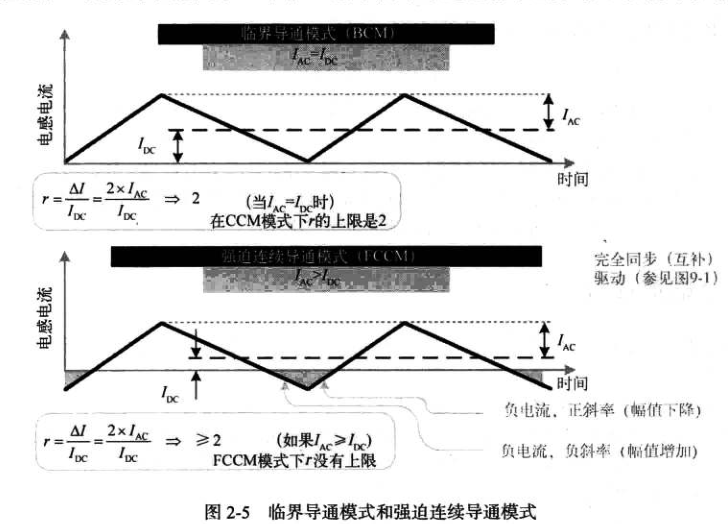
为什么是先给出r呢？不给出L呢？
r实际设计上有有经验，一般是0.3~0.5之间，一旦确定r，给定工况和开关频率下的L值就确定了。
r的最优值
r=0.4时，对变压器的尺寸和其他元器件的应力(电压电流应力)都处于相较于其他值有更大的优势。下图虽然是以降压拓扑的电容电流为例，但其其能量曲线使用与所有拓扑，电容电流rms值随着r增加而增加。
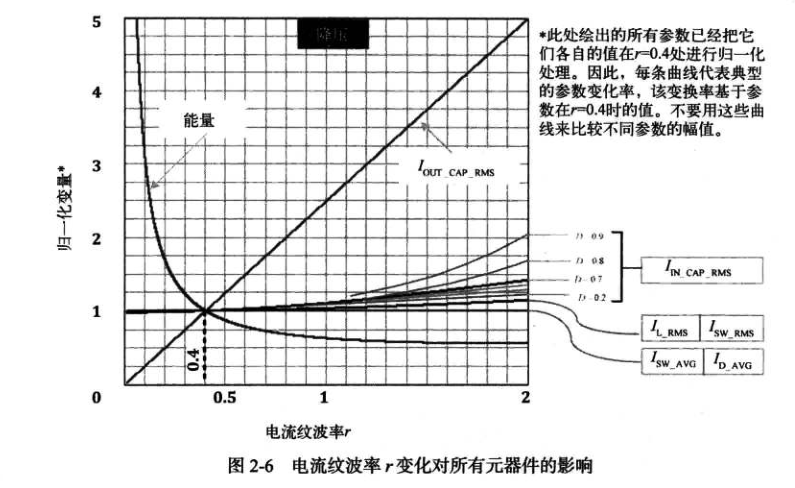
是电感尺寸还是电感值
在磁芯上绕制不同匝数的线圈，就可以得到不同的电感值，所以电感值不一定与电感尺寸相关。但实际功率变换器中，它们经常相关。
因为工况确定的情况下，工况确定是指负载电流和输入输出电压确定，Idc也确定。这种情况下唯一能使r减小的方法就是让纹波更小，而纹波又是由伏秒积确定的，所以提高电感值来减小纹波，
但是一定量的纹波无疑是有益的。
例如，工况改变，如负载电流增加，那么Idc增加后，为了保持r值的最优，需要同比增加纹波，为此不得不减小L，而非增加L
频率对电感尺寸的影响
下面的讨论使用所有拓扑
其他量都不改变，开关频率加倍，则伏秒积加倍，因为ton和toff的时间减半了，既然△i可以用单位电感的伏秒积表示，那么它也会减半。由于Idc没变，r=△i/idc,所以r也会减半。
那么要重新吧r设置为最优值0.4，就需要吧L减半，那么所以电感尺寸变小了，电感处理能量的公式是1/2*L*Ipeak2,L减半，Ipeak不变。
所以认为电感尺寸与频率成反比
还要注意电感电应力与频率无关。
负载电流对电感值和尺寸的影响
若负载电流加倍，输入输出电压和占空比不变，r值减半，虽然△I没变，但是Idc加倍了，为了保持最优r，所以△I也应加倍，即L减半。
所以一般认为电感值与负载电流减半
电感尺寸与负载电流成正比，负载电流加倍，l减半，那么电感处理能量为1/2*L*（Ipeak）²加倍，Ipeak=Idc（1+r/2）=Idc+△I.
供应商如何标注成品电感的额定电流以及如何选择电感？
绝大多数供应商将默认Idc（最大允许通过的直流电流）=Isat（电感饱和：电感在磁芯饱和前允许通过的最大电流）
给定应用中需要考虑的电感电流额定值
以下6点因素可以影响开关的迅速关断，从而使其免受电感饱和的影响
使用电流I × L 和负载缩放法快速选择电感
1. L x I = 伏秒积/电流纹波率 (适用于所有拓扑)
2. 如果从应用条件中知道伏秒积，并设置了r的目标值，就能计算出L x I ,如果知道I 就能求出L,并且要知道L与I成反比
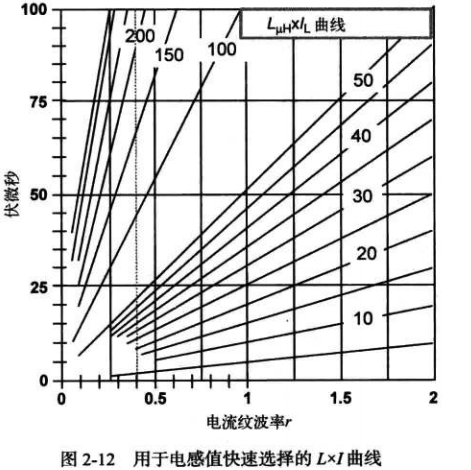
使用L×I快速选择电感的实例
基本的磁定义：研究磁芯中磁场的工作原理,一下采用MKS单位制"米-千克-秒"
1. H 磁场强度，（也成为磁场密度、磁化力、外加场），单位A/m
2. B 磁通密度，（也成为磁感应强度），单位是特斯拉(T)或者韦伯每平米(Wb/m^2)
3. 
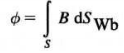磁通量,是B在特定表面积上的积分，单位是韦伯(Wb)
4. B=uH,u是磁性材料的磁导率，实际上偏向写B=ucH,c是u的下标，uc=u*u0，u0是空气的磁导率
5. 磁通量与匝数成正比，电感量与L=N*φ/I,其中N为匝数，φ为磁通，I为流过线圈的电流，所以L与N^2成正比
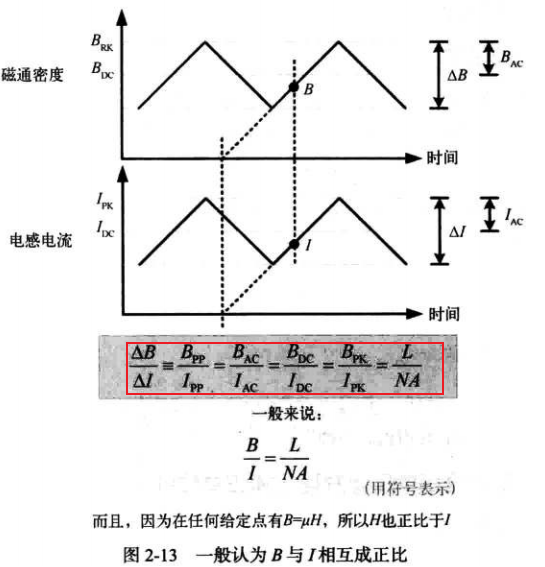
7. 不要轻易增加匝数，对于B与I的公式，如上图。不增加尺寸，增加匝数时（尺寸表示：磁芯截面积的尺寸，A），L是正比于N^2，所以在增加匝数的同时，L比N增加的更快，当增加匝数而不增加尺寸时，B磁通密度的公式，分子比分母增加更快，导致B磁通密度暴涨，导致磁芯饱和，从而失效
8. 所以电感设计前提是：给定应用中，电感值越大，电感的尺寸就越大（尺寸指的的是中心磁柱截面积，缩写为A或Ae）
9.一般磁通密度B为0.3T及以上时。磁芯开始饱和
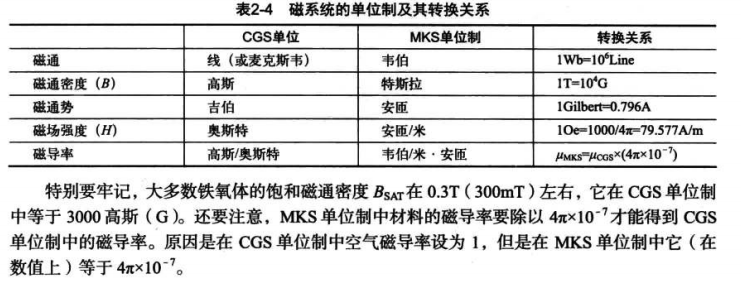
10.有两种单位制度，通用的为MKS(米-千克-秒)，CGS(厘米-克-秒)
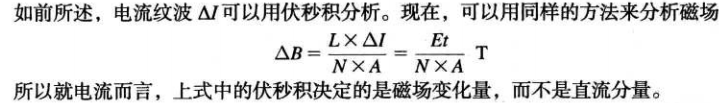
设计电感的一般步骤：
输入电压为宽电压的话如90-265vac，先选择“最恶劣的输入电压”开始设计，对于bulk拓扑Vinmax开始，对于升压或升降压，从Vinmin开始设计，因为这些电压都是电感峰值电流达到最大值对应的电压
