HDLbits day9

4、More Circuits

4.1、Rule 90

规则 90是一个具有有趣特性的一维元胞自动机。

规则很简单。有一个一维的单元格数组（开或关）。在每个时间步，每个单元的下一个状态是单元的两个当前邻居的 XOR。下表是表达此规则的更详细的方式，其中单元格的下一个状态是其自身及其两个邻居的函数：

Left	Center	Right	Center's next state
1	1	1	0
1	1	0	1
1	0	1	0
1	0	0	1
0	1	1	1
0	1	0	0
0	0	1	1
0	0	0	0

 

（“规则 90”的名称来自阅读“下一个状态”列：01011010 是十进制的 90。）

在此电路中，创建一个 512 单元系统 ( q[511:0] )，并在每个时钟周期前进一个时间步长。加载输入指示系统的状态应加载data[511:0]。假设边界（q[-1]和q[512]）都为零（关闭）。

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output [511:0] q ); 

    //center的下一个状态是center的左右两个变量异或而得
    always@(posedge clk)
        begin
            if(load)
                q<=data;
            else
                q<={1'b0,q[511:1]}^{q[510:0],1'b0};
        end
endmodule

4.2、Rule 110

规则 110是一个具有有趣特性（例如图灵完备）的一维元胞自动机。

有一个一维的单元格数组（开或关）。在每个时间步，每个单元格的状态都会发生变化。在规则 110 中，每个单元格的下一个状态仅取决于它自己和它的两个邻居，如下表所示：

Left	Center	Right	Center's next state
1	1	1	0
1	1	0	1
1	0	1	1
1	0	0	0
0	1	1	1
0	1	0	1
0	0	1	1
0	0	0	0

在此电路中，创建一个 512 单元系统 ( q[511:0] )，并在每个时钟周期前进一个时间步长。加载输入指示系统的状态应加载data[511:0]。假设边界（q[-1]和q[512]）都为零（关闭）。（“规则 110”的名称来自阅读“下一个状态”列：01101110 是十进制的 110。）

module top_module(
    input clk,
    input load,
    input [511:0] data,
    output [511:0] q
); 
    wire [511:0] L={1'b0,q[511:1]};
    wire [511:0] R={q[510:0],1'b0};
    
    //wire [511:0] R,L;
    //assign L={1'b0,q[511:1]};
    //assign R={q[510:0],1'b0};
    always@(posedge clk)
        begin
            if(load)
                q<=data;
            else
                q<=(q&~R)|(~L&R)|(~q&R);//有真值表化简所得公式
        end
    

endmodule

4.3、Conway's Game of Life 16x16

康威的生命游戏是一个二维元胞自动机。

“游戏”是在一个二维单元格上进行的，其中每个单元格要么是 1（活着），要么是 0（死去）。在每个时间步，每个单元格都会根据它拥有的邻居数量来改变状态：

• 0-1 邻居：单元格变为 0。
• 2个邻居：小区状态不变。
• 3 个邻居：单元格变为 1。
• 4 个以上的邻居：单元格变为 0。

该游戏是为无限网格制定的。在这个电路中，我们将使用 16x16 网格。为了让事情更有趣，我们将使用一个 16x16 的环形，其中边环绕到网格的另一边。例如，角单元 (0,0) 有 8 个邻居：(15,1) , (15,0) , (15,15) , (0,1) , (0,15) , (1,1)、(1,0)和(1,15)。16x16 的网格由一个长度为 256 的向量表示，其中每行 16 个单元格由一个子向量表示：q[15:0] 为第 0 行，q[31:16] 为第 1 行，以此类推（此工具接受 SystemVerilog，因此您可以根据需要使用 2D 向量。）

• load：在下一个时钟沿将数据加载到q中，用于加载初始状态。
• q：游戏的 16x16 当前状态，每个时钟周期更新。

游戏状态应该在每个时钟周期前进一个时间步长。

module top_module(
    input clk,
    input load,
    input [255:0] data,
    output [255:0] q ); 
    
    reg [15:0] q_2d [15:0];
    reg [15:0] q_next [15:0];
    reg [3:0] sum;
    integer i,j;
    
    //把一维输入的数据转换为二维数据
    always@(posedge clk)
        begin
            if(load)
                begin
                    for(i=0;i<=15;i=i+1)
                        for(j=0;j<=15;j=j+1)
                            begin
                                q_2d[i][j]<=data[i*16+j];
                            end
                end
            else
                q_2d<=q_next;
        end
    
    always@(*)
        begin
            for(i=0;i<=15;i=i+1)
                for(j=0;j<=15;j=j+1)
                    begin
                         if(i==0 && j==0)//左上角
                             sum=q_2d[15][1]+q_2d[15][0]+q_2d[15][15]+q_2d[0][1]+q_2d[0][15]+q_2d[1][0]+q_2d[1][1]+q_2d[1][15];
                        else if(i==0 && j==15)//右上角
                            sum=q_2d[0][0]+q_2d[0][14]+q_2d[15][0]+q_2d[15][14]+q_2d[15][15]+q_2d[1][0]+q_2d[1][14]+q_2d[1][15];
                        else if(i==15 && j==0)//左下角
                            sum=q_2d[15][1]+q_2d[15][15]+q_2d[14][0]+q_2d[14][15]+q_2d[14][1]+q_2d[0][0]+q_2d[0][1]+q_2d[0][15];
                        else if(i==15 && j==15)//右下角
                            sum=q_2d[15][0]+q_2d[15][14]+q_2d[14][15]+q_2d[14][0]+q_2d[14][14]+q_2d[0][0]+q_2d[0][15]+q_2d[0][14];
                        else if(i==0)//上边界
                            sum=q_2d[0][j-1]+q_2d[0][j+1]+q_2d[1][j-1]+q_2d[1][j]+q_2d[1][j+1]+q_2d[15][j-1]+q_2d[15][j]+q_2d[15][j+1];
                        else if(i==15)//下边界
                            sum=q_2d[15][j-1]+q_2d[15][j+1]+q_2d[0][j-1]+q_2d[0][j]+q_2d[0][j+1]+q_2d[14][j-1]+q_2d[14][j]+q_2d[14][j+1];
                        else if(j==0)//左边界
                            sum=q_2d[i][1]+q_2d[i][15]+q_2d[i-1][0]+q_2d[i-1][15]+q_2d[i-1][1]+q_2d[i+1][0]+q_2d[i+1][1]+q_2d[i+1][15];
                        else if(j==15)//右边界
                            sum=q_2d[i][0]+q_2d[i][14]+q_2d[i-1][0]+q_2d[i-1][14]+q_2d[i-1][15]+q_2d[i+1][0]+q_2d[i+1][14]+q_2d[i+1][15];
                        else  //中间元素
                            sum=q_2d[i-1][j]+q_2d[i-1][j-1]+q_2d[i-1][j+1]+q_2d[i][j-1]+q_2d[i][j+1]+q_2d[i+1][j]+q_2d[i+1][j-1]+q_2d[i+1][j+1];

                        case(sum)
                            4'd2:q_next[i][j]=q_2d[i][j];
                            4'd3:q_next[i][j]=1'b1;
                            default:q_next[i][j]=1'b0;
                        endcase
                    end
        end
    
    //把二维数组转成一维数组输出
    genvar m,n;
    generate
        for(m=0;m<=15;m=m+1)
            begin:hang
                for(n=0;n<=15;n=n+1)
                    begin:lie
                        assign q[m*16+n]=q_2d[m][n];
                    end
            end
    endgenerate

endmodule

 5、Finite State Machines

5.1、Simple FSM 1(asynchronous reset)

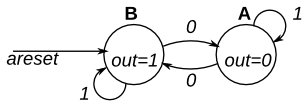
这是一个具有两种状态的摩尔状态机，一种输入和一种输出。实现这个状态机。请注意，重置状态为 B。

本练习与fsm1s相同，但使用异步复位。

 

module top_module(
    input clk,
    input areset,    // Asynchronous reset to state B
    input in,
    output out);//  

    parameter A=0, B=1; 
    reg state, next_state;

    always @(*) begin    // This is a combinational always block
        // State transition logic
        case(state)
            A:begin
                if(in==1'b1)
                    next_state<=A;
                else
                    next_state<=B;
            end
            B:begin
                if(in==1'b1)
                    next_state<=B;
                else
                    next_state<=A;
            end
        endcase
    end

    always @(posedge clk, posedge areset) begin    // This is a sequential always block
        // State flip-flops with asynchronous reset
        if(areset)
            state<=B;
        else
            state<=next_state;
    end

    // Output logic
    // assign out = (state == ...);
    assign out=(state==B);

endmodule

 5.2、Simple FSM1（Synchronous reset）

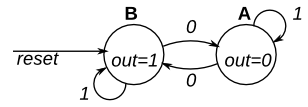
这是一个具有两种状态的摩尔状态机，一种输入和一种输出。实现这个状态机。请注意，重置状态为 B。

本练习与fsm1相同，但使用同步复位。

 

一开始报错，原因如下：

第一、题目给出的else位置有问题；

第二、在同一个always语句块中编写所有的逻辑，这里必须使用延迟赋值语句，保证上一个逻辑完成以后再进行下一个逻辑

// Note the Verilog-1995 module declaration syntax here:
module top_module(clk, reset, in, out);
    input clk;
    input reset;    // Synchronous reset to state B
    input in;
    output out;//  
    reg out;

    // Fill in state name declarations
    parameter A=0,B=1;
    reg present_state, next_state;

    always @(posedge clk) begin
        if (reset) begin  
            // Fill in reset logic
            next_state = B;
        end 
        else begin
            case (present_state)
                // Fill in state transition logic
                 A:begin
                    if(in==1'b1)
                       next_state=A;
                    else
                        next_state=B;
                end
                B:begin
                    if(in==1'b1)
                        next_state=B;
                    else
                        next_state=A;
                end
            endcase
        end
         // State flip-flops状态触发器，注意这里用的延迟赋值语句
            present_state = next_state;

            case (present_state)
                // Fill in output logic
                A:out=1'b0;
                B:out=1'b1;
            endcase
    end

endmodule

 5.3、Simple FSM2（asynchronous reset）

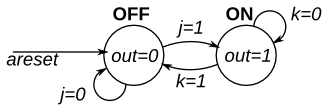
这是一个具有两个状态、两个输入和一个输出的摩尔状态机。实现这个状态机。

这个练习和fsm2s一样，但使用异步复位。

 

module top_module(
    input clk,
    input areset,    // Asynchronous reset to OFF
    input j,
    input k,
    output out); //  

    parameter OFF=0, ON=1; 
    reg state, next_state;

    always @(*) begin
        // State transition logic
        case(state)
            OFF:next_state<=(j==1'b1)?ON:OFF;
            ON: next_state<=(k==1'b1)?OFF:ON;
        endcase
    end

    always @(posedge clk, posedge areset) begin
        // State flip-flops with asynchronous reset
        if(areset)
            state<=OFF;
        else
            state<=next_state;
            
    end

    // Output logic
    // assign out = (state == ...);
    assign out=(state==OFF)?0:1;

endmodule

 5.4、Simple FSM2（Synchronous reset）

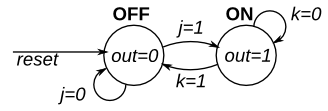
这是一个具有两个状态、两个输入和一个输出的摩尔状态机。实现这个状态机。

本练习与fsm2相同，但使用同步复位。

 

module top_module(
    input clk,
    input reset,    // Synchronous reset to OFF
    input j,
    input k,
    output out); //  

    parameter OFF=0, ON=1; 
    reg state, next_state;

    always @(*) begin
        // State transition logic
        case(state)
            OFF:next_state<=(j==1'b1)?ON:OFF;
            ON: next_state<=(k==1'b1)?OFF:ON;
        endcase
    end

    always @(posedge clk) begin
        // State flip-flops with synchronous reset
        if(reset)
            state<=OFF;
        else
            state<=next_state;
    end

    // Output logic
    // assign out = (state == ...);
    assign out=(state==ON);

endmodule

 5.5、Simple state transition3

以下是一输入一输出四状态的摩尔状态机的状态转移表。使用以下状态编码：A=2'b00, B=2'b01, C=2'b10, D=2'b11。

仅实现此状态机的状态转换逻辑和输出逻辑（组合逻辑部分）。给定当前state ，计算next_state和输出 

State	Next state		Output
	in=0	in=1
A	A	B	0
B	C	B	0
C	A	D	0
D	C	B	1

module top_module(
    input in,
    input [1:0] state,
    output [1:0] next_state,
    output out); //

    parameter A=0, B=1, C=2, D=3;

    // State transition logic: next_state = f(state, in)
    //always@(posedge clk)
    always@(*)
        begin
            case(state)
                A:next_state<=(in==1'b1)?B:A;
                B:next_state<=(in==1'b1)?B:C;
                C:next_state<=(in==1'b1)?D:A;
                D:next_state<=(in==1'b1)?B:C;
            endcase
        end

    // Output logic:  out = f(state) for a Moore state machine
    always@(*)
        begin
            out<=(state==D);
        end

endmodule

5.6、simple one-hot state transitions 3

以下是一输入一输出四状态的摩尔状态机的状态转移表。使用以下单热状态编码：A=4'b0001, B=4'b0010, C=4'b0100, D=4'b1000。

假设 one-hot 编码，通过检查导出状态转换和输出逻辑方程。仅实现此状态机的状态转换逻辑和输出逻辑（组合逻辑部分）。（测试台将使用非一个热输入进行测试，以确保您不会尝试做更复杂的事情）。

State	Next state		Output
	in=0	in=1
A	A	B	0
B	C	B	0
C	A	D	0
D	C	B	1

module top_module(
    input in,
    input [3:0] state,
    output [3:0] next_state,
    output out); //

    parameter A=0, B=1, C=2, D=3;

    // State transition logic: Derive an equation for each state flip-flop.
    assign next_state[A] = (state[A]&~in)|(state[C]&~in);
    assign next_state[B] = (state[A]&in)|(state[B]&in)|(state[D]&in);
    assign next_state[C] = (state[B]&~in)|(state[D]&~in);
    assign next_state[D] = (state[C]&in);

    // Output logic: 
    assign out = (state[D]==1'b1);

endmodule

5.7、Simple FSM3(asynchronous reset)

以下是一输入一输出四状态的摩尔状态机的状态转移表。实现这个状态机。包括将 FSM 重置为状态 A 的异步重置。

State	Next state		Output
	in=0	in=1
A	A	B	0
B	C	B	0
C	A	D	0
D	C	B	1

module top_module(
    input clk,
    input in,
    input areset,
    output out); //

    parameter A=0,B=1,C=2,D=3;
    reg[1:0] state,next_state;
    
    // State transition logic
    always@(*)
        begin
            case(state)
                A:next_state<=(in==1'b0)?A:B;
                B:next_state<=(in==1'b0)?C:B;
                C:next_state<=(in==1'b0)?A:D;
                D:next_state<=(in==1'b0)?C:B;
            endcase
        end
    
    // State flip-flops with asynchronous reset
    always@(posedge clk or posedge areset)
        begin
            if(areset)
                state<=A;
            else
                state<=next_state;
        end

    // Output logic
    always@(*)
        begin
            out<=(state==D);
        end

endmodule

5.8、Fsm3s

以下是一输入一输出四状态的摩尔状态机的状态转移表。实现这个状态机。包括将 FSM 重置为状态 A 的同步重置。

State	Next state		Output
	in=0	in=1
A	A	B	0
B	C	B	0
C	A	D	0
D	C	B	1

 

module top_module(
    input clk,
    input in,
    input reset,
    output out); //

    parameter A=0,B=1,C=2,D=3;
    reg[1:0] state,next_state;
    
    // State transition logic
    always@(*)
        begin
            case(state)
                A:next_state<=(in==1'b0)?A:B;
                B:next_state<=(in==1'b0)?C:B;
                C:next_state<=(in==1'b0)?A:D;
                D:next_state<=(in==1'b0)?C:B;
            endcase
        end

    // State flip-flops with synchronous reset
    always@(posedge clk)
        begin
            if(reset) state<=A;
            else
                state<=next_state;
        end

    // Output logic
    assign out=(state==D);

endmodule

 5.9、Exams/ece241 2013 q4

　　大型水库可为多个用户提供服务。为了使水位足够高，三个传感器以5英寸的间隔垂直放置。当水位高于最高传感器（S3）时，输入流量应为零。当液位低于最低传感器（S1）时，流量应最大（标称流量阀和辅助流量阀均打开）。当水位在上下传感器之间时，流速由两个因素决定：水位和最后一个传感器变化之前的水位。每种水位都有一个与之相关的标称流速，如下表所示。如果传感器变化表明先前的液位低于当前的液位，则应进行标称流速。如果先前的水平高于当前水平，则应通过打开辅助流量阀（由ΔFR控制）来增加流量。
　　绘制水库控制器的摩尔模型状态图。清楚地指出每个状态的所有状态转换和输出。 FSM的输入为S1，S2和S3。输出为FR1，FR2，FR3和ΔFR。

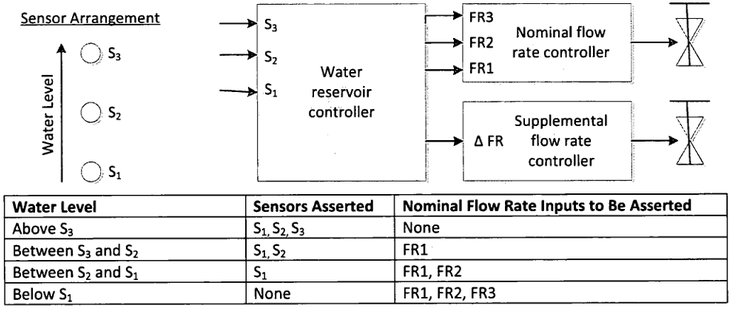
1）这是一个水位控制系统，S1,S2,S3是三个水位传感器。FR3,FR2,FR1为三个控制水流量的开关，开得越多流量越大。ΔFR是检测水位变化的标志。

2）设计一个状态机判断水位并根据水位选择流量开关

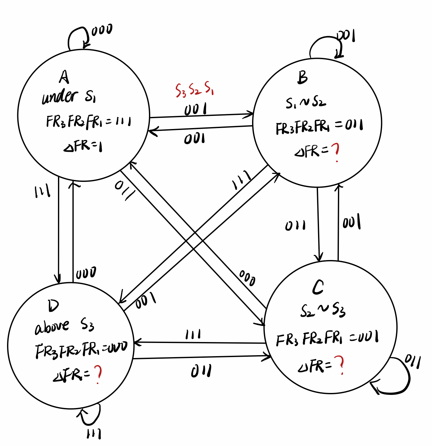
3）一共有四种状态，A表示水位在S1下面，FR1、FR2、FR3都为1；B表示水位在S1与S2之间，FR1、FR2都为1；C表示水位在S2与S3之间，FR1为1；D表示水位在S3以上，FR1、FR2、FR3都为0。

4）输入信号为S3S2S1，其中S1为1就表示水位在S1之上。然后如果之前的水阀数量比当前的多，那么ΔFR就是1；如果比现在的少，那么ΔFR就是0；如果水位保持不变，ΔFR也保持不变。由于最低状态只能比当前得多，所以ΔFR一直都会是1，就算是水位不变，也要保持ΔFR是1；同理最高水位一定是比之前的高，所以ΔFR一直是0。

5）官方答案采用了6种状态，加考虑了dfr的变化，代码更简单，6种状态转换图的描绘参考博文：

http://m.bubuko.com/infodetail-3750752.html

module top_module (
    input clk,
    input reset,
    input [3:1] s,
    output fr3,
    output fr2,
    output fr1,
    output dfr
); 

    parameter A=0,B=1,C=2,D=3;
    reg[1:0] state,next_state;
    reg store_dfr;
    reg[2:0] store_fr;
    
    assign store_fr={fr3,fr2,fr1};
    assign store_dfr=dfr;
    

    always@(*)
        begin
            case(state)
                A:case(s)
                    3'b000:next_state<=A;
                    3'b001:next_state<=B;
                    3'b011:next_state<=C;
                    3'b111:next_state<=D;
                endcase
                B:case(s)
                    3'b000:next_state<=A;
                    3'b001:next_state<=B;
                    3'b011:next_state<=C;
                    3'b111:next_state<=D;
                endcase
                C:case(s)
                    3'b000:next_state<=A;
                    3'b001:next_state<=B;
                    3'b011:next_state<=C;
                    3'b111:next_state<=D;
                endcase
                D:case(s)
                    3'b000:next_state<=A;
                    3'b001:next_state<=B;
                    3'b011:next_state<=C;
                    3'b111:next_state<=D;
                endcase
            endcase
        end
  
    always@(posedge clk)
        begin
            if(reset)
                state<=A;
            else
                state<=next_state;
        end
    
    always@(posedge clk)
        begin
            if(reset)
                dfr<=1;
            else
                begin
                    if(state>next_state)
                        dfr<=1;
                    else if(state<next_state)
                        dfr<=0;
                    else
                        dfr<=dfr;
                end
        end
    
    always@(posedge clk)
        begin
            if(reset) {fr3,fr2,fr1}<=3'b111;
            else
                begin
                    case(next_state)
                        A:{fr3,fr2,fr1}<=3'b111;
                        B:{fr3,fr2,fr1}<=3'b011;
                        C:{fr3,fr2,fr1}<=3'b001;
                        D:{fr3,fr2,fr1}<=3'b000;
                    endcase
                end
        end
    
endmodule