HDLbits day6

2、Multiplexers

2.1、2-to-1 multiplexer

创建一位宽的 2 对 1 多路复用器。当 sel=0 时，选择 a。当 sel=1 时，选择 b。

module top_module( 
    input a, b, sel,
    output out ); 

    assign out=sel?b:a;
endmodule

2.2、2-to-1 bus multiplexer

创建一个 100 位宽的 2 对 1 多路复用器。当 sel=0 时，选择 a。当 sel=1 时，选择 b。

module top_module( 
    input [99:0] a, b,
    input sel,
    output [99:0] out );

    assign out=sel?b:a;
endmodule

2.3、9-to-1 multiplexer

创建一个 16 位宽的 9 对 1 多路复用器。sel=0 选择 a，sel=1 选择 b，等等。对于未使用的情况（sel=9 到 15），将所有输出位设置为“1”。

module top_module( 
    input [15:0] a, b, c, d, e, f, g, h, i,
    input [3:0] sel,
    output [15:0] out );
    
    always@(*)
        begin
            case(sel)
                4'b0000:out=a;
                4'b0001:out=b;
                4'b0010:out=c;
                4'b0011:out=d;
                4'b0100:out=e;
                4'b0101:out=f;
                4'b0110:out=g;
                4'b0111:out=h;
                4'b1000:out=i;
                default:out={16{1'b1}};
            endcase
        end

endmodule

2.4、256-to-1 multiplexer

创建一个 1 位宽、256 对 1 的多路复用器。256 个输入全部打包成一个 256 位输入向量。sel=0 应该选择in[0]， sel=1 选择[1]中的位， sel=2 选择[2]中的位，等等。

module top_module( 
    input [255:0] in,
    input [7:0] sel,
    output out );
//用if  else语句会创建闩锁
    assign out=in[sel];
endmodule

2.5、256-to-1 4-bit multiplexer

创建一个 4 位宽、256 对 1 的多路复用器。256 个 4 位输入全部打包成一个 1024 位输入向量。sel=0 应该选择[3:0]中的位， sel=1 选择[7:4]中的位， sel=2 选择[11:8]中的位等。

注释部分代码的报错：Error (10734): Verilog HDL error at top_module.v(10): sel is not a constant

冒号“：”操作符：A[a : b]的含义理解为vectorA中选择位的范围，目前其中a和b只能是常数，而不能是变量。此处应该区分动态数组。

所以，应该将in[(sel*4)+3:sel*4]中的四个bit，用拼接符{}包括起来，{in[sel*4+3], in[sel*4+2], in[sel*4+1], in[sel*4+0]} 组成新的位宽为4的向量后再赋值给out。

module top_module( 
    input [1023:0] in,
    input [7:0] sel,
    output [3:0] out );
    
    //assign out=in[3+4*sel:4*sel];
 
    assign out={in[3+4*sel],in[2+4*sel],in[1+4*sel],in[4*sel]};
endmodule

 

3、 Arithmetic Circuits

3.1、Half adder

创建一个半加法器。半加器将两位相加（没有进位）并产生和和进位。

a	b	sum	sout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

 

module top_module( 
    input a, b,
    output cout, sum );

    //assign {cout,sum}=a+b;
    
    assign cout=a&b;
    assign sum=a^b;
endmodule

3.2、Full adder

创建一个全加器。全加器将三位相加（包括进位）并产生和和进位。

a	b	cin	sum	cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

module top_module( 
    input a, b, cin,
    output cout, sum );

    //assign {cout,sum}=a+b+cin;
    
    assign sum=(~a)&(~b)&cin|(~a)&b&(~cin)|a&(~b)&(~cin)|a&b&cin;
    assign cout=a&b|a&cin|b&cin;
endmodule

3.3、3-bit binary adder

现在您已经知道如何构建一个全加器，创建 3 个实例来创建一个 3 位二进制波纹进位加法器。加法器将两个 3 位数字和一个进位相加以产生一个 3 位和并进位。为了鼓励您实际实例化全加器，还要输出纹波进位加法器中每个全加器的进位。cout[2] 是最后一个全加器的最终进位，也是您通常看到的进位。

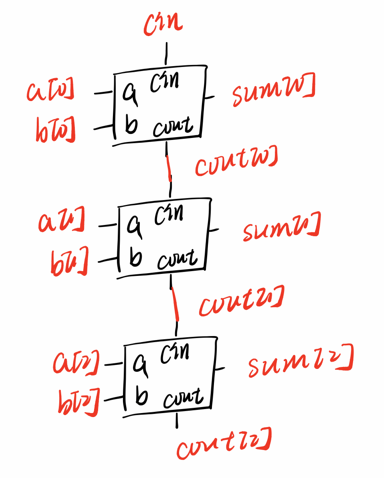
module top_module( 
    input [2:0] a, b,
    input cin,
    output [2:0] cout,
    output [2:0] sum );

    wire w1,w2;
    add1 U1(a[0],b[0],cin,cout[0],sum[0]);
    add1 U2(a[1],b[1],cout[0],cout[1],sum[1]);
    add1 U3(a[2],b[2],cout[1],cout[2],sum[2]);
    
    
endmodule

module add1(
    input a,
    input b,
    input cin,
    output cout,
    output sum);
    
    assign {cout,sum}=a+b+cin;
    
endmodule

3.4、Adder

实现以下电路：

（“FA”是一个全加器）

 

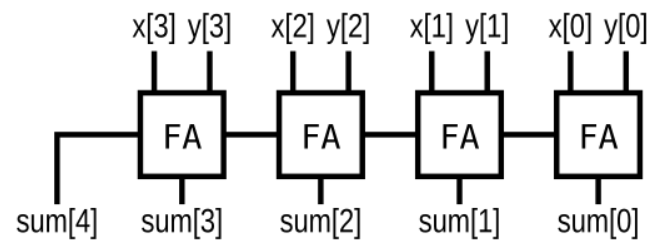
module top_module (
    input [3:0] x,
    input [3:0] y, 
    output [4:0] sum);

    wire w1,w2,w3;
    FA U1(.a(x[0]),.b(y[0]),.sum(sum[0]),.cout(w1));
    FA U2(.a(x[1]),.b(y[1]),.cin(w1),.sum(sum[1]),.cout(w2));
    FA U3(.a(x[2]),.b(y[2]),.cin(w2),.sum(sum[2]),.cout(w3));
    FA U4(.a(x[3]),.b(y[3]),.cin(w3),.sum(sum[3]),.cout(sum[4]));
endmodule

module FA(input a,input b,input cin,output sum,output cout);
    assign {cout,sum}=a+b+cin;
endmodule

 3.5、Signed addition overflow

假设您有两个 8 位 2 的补码，a[7:0] 和 b[7:0]。这些数字相加产生 s[7:0]。还要计算是否发生了（有符号的）溢出。

1）当两个正数相加产生负结果或两个负数相加产生正结果时，会发生 有符号溢出。

2）有几种检测溢出的方法：它可以通过比较输入和输出数的符号来计算，或者从位 n 和 n-1 的进位推导出来。

module top_module (
    input [7:0] a,
    input [7:0] b,
    output [7:0] s,
    output overflow
); //
 
    // assign s = ...
    // assign overflow = ...
    assign s=a+b;
    assign overflow=a[7]&b[7]&(~s[7])|(~a[7])&(~b[7])&s[7];
    //assign overflow=a[7]^b[7]~^s[7];错误原因：a为01100_0000，b1100_0000，得s为1_0000_0000，溢出，但是带入公式结果不符合实际

endmodule

3.6、100-bit binary adder

创建一个 100 位二进制加法器。加法器将两个 100 位数字和一个进位相加，产生一个 100 位和并执行。

module top_module( 
    input [99:0] a, b,
    input cin,
    output cout,
    output [99:0] sum );

    assign {cout,sum}=a+b+cin;
endmodule

3.7、4-digit BCD adder

为您提供了一个名为bcd_fadd的 BCD（二进制编码的十进制）一位加法器，它将两个 BCD 数字和进位相加，并产生一个和和进位。

module bcd_fadd (
    input [3:0] a,
    input [3:0] b,
    input     cin,
    output   cout,
    output [3:0] sum );

实例化 4 个bcd_fadd副本以创建一个 4 位 BCD 波纹进位加法器。您的加法器应该将两个 4 位 BCD 数字（打包成 16 位向量）和一个进位相加，以产生一个 4 位和并执行。

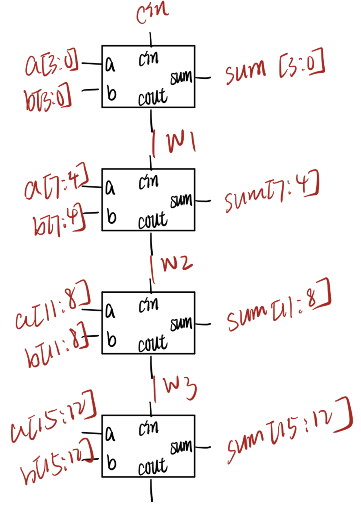
module top_module ( 
    input [15:0] a, b,
    input cin,
    output cout,
    output [15:0] sum );

    wire w1,w2,w3;
    bcd_fadd U1(.a(a[3:0]),.b(b[3:0]),.cin(cin),.sum(sum[3:0]),.cout(w1));
    bcd_fadd U2(.a(a[7:4]),.b(b[7:4]),.cin(w1),.sum(sum[7:4]),.cout(w2));
    bcd_fadd U3(.a(a[11:8]),.b(b[11:8]),.cin(w2),.sum(sum[11:8]),.cout(w3));
    bcd_fadd U4(.a(a[15:12]),.b(b[15:12]),.cin(w3),.sum(sum[15:12]),.cout(cout));
endmodule

 

四、Karnaugh Map to Circuit

4.1、3-variable

实现下面卡诺图描述的电路。

1）在编码之前尝试简化 k-map。尝试和积和积和形式。

2）我们无法检查您是否有 k-map 的最佳简化。但是我们可以检查你的归约是否等价，我们可以检查你是否可以将 k-map 转换为电路。

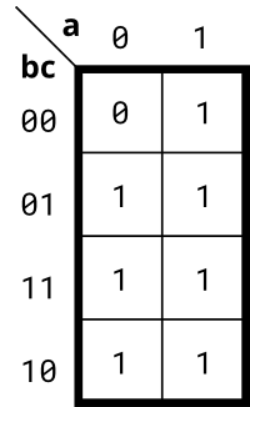
module top_module(
    input a,
    input b,
    input c,
    output out  ); 
    
   assign out=a|b|c;
endmodule

4.2、4-variable

实现下面卡诺图描述的电路。

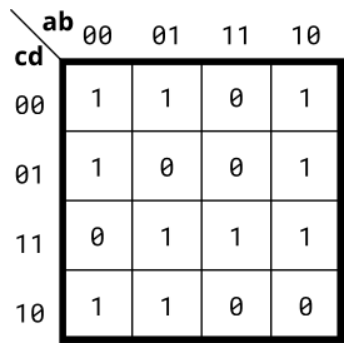
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out=(~b)&(~c)|(~a)&(~d)|a&c&d|(~a)&b&c;
endmodule

4.3、4-variable

实现下面卡诺图描述的电路。

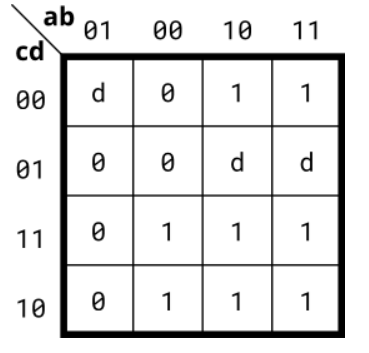
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out=a|(~b)&c|b&(~c)&(~d);
endmodule

4.4、4-variable

实现下面卡诺图描述的电路。

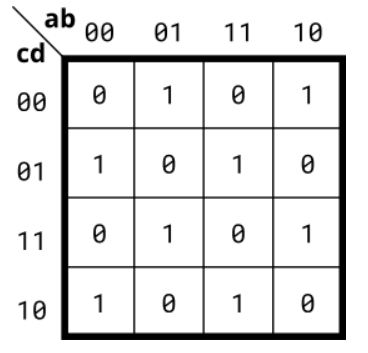
module top_module(
    input a,
    input b,
    input c,
    input d,
    output out  ); 

    assign out = (~a&~b&~c&d)|(~a&b&~c&~d)|(a&b&~c&d)|(a&~b&~c&~d)|(~a&b&c&d)|(a&~b&c&d)|(~a&~b&c&~d)|(a&b&c&~d);
endmodule

4.5、Minimum SOP and POS

具有四个输入（a、b、c、d）的单输出数字系统在输入上出现 2、7 或 15 时生成逻辑 1，当输入上出现 0、1、4、5、6 、9、10、13 或 14 出现时生成逻辑 0。数字 3、8、11 和 12 的输入条件在此系统中永远不会出现。例如，7 对应于 a、b、c、d 分别设置为 0、1、1、1。

确定最小SOP形式(积之和 最小项)的输出out_sop，以及最小POS形式(和之积 最大项)的输出out_pos。

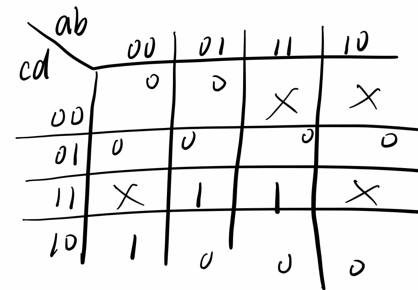
module top_module (
    input a,
    input b,
    input c,
    input d,
    output out_sop,
    output out_pos
); 
    assign out_sop=c&d|(~a)&(~b)&c;
    assign out_pos=c&(~a|b)&(~b|d);

endmodule

4.6、Karnaugh map

考虑下面卡诺图中所示 的函数f 。

实现这个功能。d是不关心，这意味着您可以选择输出任何方便的值。

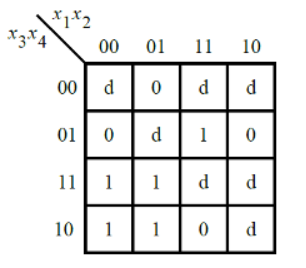
module top_module (
    input [4:1] x, 
    output f );

    assign f = (~x[1]&x[3])|(x[2]&x[4]);
endmodule

4.7、Karnaugh map

考虑下面卡诺图中所示的函数f 。实现这个功能。

（原始考试问题要求简化 SOP 和 POS 形式的函数。）

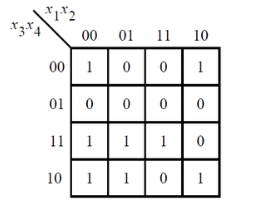
module top_module (
    input [4:1] x,
    output f
); 
    
    assign f=(~x[2]&~x[4])|(~x[1]&x[3])|(x[2]&x[3]&x[4]);

endmodule

4.8、K-map implemented with a multiplexer

对于下面的卡诺图，给出使用一个 4 对 1 多路复用器和尽可能多的 2 对 1 多路复用器的电路实现，但使用尽可能少。不允许使用任何其他逻辑门，并且必须使用a和b作为多路复用器选择器输入，如下面的 4 对 1 多路复用器所示。

您只实现了标记为top_module的部分，以便整个电路（包括 4 对 1 多路复用器）实现 K-map。

module top_module (
    input c,
    input d,
    output [3:0] mux_in
); 
    assign mux_in[0]=c|d;
    assign mux_in[1]=1'b0;
    assign mux_in[2]=~d;
    assign mux_in[3]=c&d;

endmodule