BZOJ1009: [HNOI2008]GT考试(KMP+矩阵乘法)
Description
阿申准备报名参加GT考试,准考证号为N位数X1X2....Xn(0<=Xi<=9),他不希望准考证号上出现不吉利的数字。
他的不吉利数学A1A2...Am(0<=Ai<=9)有M位,不出现是指X1X2...Xn中没有恰好一段等于A1A2...Am. A1和X1可以为
0
Input
第一行输入N,M,K.接下来一行输入M位的数。 N<=10^9,M<=20,K<=1000
Output
阿申想知道不出现不吉利数字的号码有多少种,输出模K取余的结果.
Sample Input
4 3 100
111
111
Sample Output
81
解题思路:
首先,确定一下什么样的数字中没有不吉利数字。
1.这个数字的前缀不是不吉利数字(废话)
2.这个数字中间不包含不吉利数字(废话)
3.这个数字的后缀不是不吉利数字(废话)
那么,这个数字如果是像汉堡那样一层一层堆的话,我们可以通过尽可能阻止不吉利数字出现来完成任务。
假设数字串出现到了第 i 位,只要后缀m-1位不是不吉利数字m-1位就可以。
所以设f[i][j]为数字堆积到 i 而匹配出来了 j 位。
那么 :
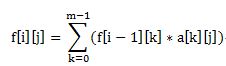
a[k][j]为预处理出来的结果,其概念为:
原串中匹配到 j 时 k 位是否可以被枚举,由于做到不重不漏地计数,每次取前一个next即可
最后由于运算简单但递推长度大,使用矩阵乘法即可。
代码:
1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 typedef long long lnt; 5 int n,m; 6 lnt K; 7 char num[100000]; 8 int nxt[100000]; 9 struct squ{ 10 lnt s[30][30]; 11 squ friend operator * (squ x,squ y) 12 { 13 squ ans; 14 for(int i=0;i<m;i++) 15 { 16 for(int j=0;j<m;j++) 17 { 18 ans.s[i][j]=0; 19 for(int k=0;k<m;k++) 20 { 21 ans.s[i][j]=(ans.s[i][j]+x.s[i][k]*y.s[k][j])%K; 22 } 23 } 24 } 25 return ans; 26 } 27 squ friend operator ^ (squ x,lnt y) 28 { 29 squ ans=x; 30 y--; 31 while(y) 32 { 33 if(y&1) 34 ans=ans*x; 35 x=x*x; 36 y=y/2; 37 } 38 return ans; 39 } 40 }f,g; 41 int main() 42 { 43 scanf("%d%d%lld",&n,&m,&K); 44 scanf("%s",num+1); 45 nxt[0]=nxt[1]=0; 46 for(int i=2,j=0;i<=m;i++) 47 { 48 while(j&&num[i]!=num[j+1]) 49 j=nxt[j]; 50 if(num[i]==num[j+1]) 51 j++; 52 nxt[i]=j; 53 } 54 for(int k=0;k<m;k++) 55 { 56 for(int j=0;j<10;j++) 57 { 58 int i=k; 59 while(i&&num[i+1]!=j+'0') 60 i=nxt[i]; 61 if(num[i+1]==j+'0') 62 i++; 63 if(i!=m) 64 g.s[i][k]=(g.s[i][k]+1)%K; 65 } 66 } 67 f=g^n; 68 lnt ans=0; 69 for(int i=0;i<m;i++) 70 { 71 ans=(ans+f.s[i][0])%K; 72 } 73 printf("%lld\n",ans); 74 return 0; 75 } 76


