NOI2018归程(Kruskal重构树)
题目描述
本题的故事发生在魔力之都,在这里我们将为你介绍一些必要的设定。 魔力之都可以抽象成一个 n 个节点、m 条边的无向连通图(节点的编号从 1 至 n)。 我们依次用 l,a 描述一条边的长度、海拔。 作为季风气候的代表城市,魔力之都时常有雨水相伴,因此道路积水总是不可避免 的。由于整个城市的排水系统连通,因此有积水的边一定是 海拔相对最低的一些边。 我们用水位线来描述降雨的程度,它的意义是:所有海拔不超过水位线的边都是有积水的。
Yazid 是一名来自魔力之都的 OIer,刚参加完 ION2018 的他将踏上归程,回到他 温暖的家。 Yazid 的家恰好在魔力之都的 1 号节点。对于接下来 Q 天,每一天 Yazid 都会告 诉你他的出发点 v ,以及当天的水位线 p。 每一天,Yazid 在出发点都拥有一辆 . 车。这辆车由于一些故障不能经过有积水的边。 Yazid 可以在任意节点下车,这样接下来他就可以步行经过有积水的边。但车会被留在 他下车的节点并不会再被使用。 • 需要特殊说明的是,第二天车会被重置,这意味着: – 车会在新的出发点被准备好。 – Yazid 不能利用之前在某处停放的车。 Yazid 非常讨厌在雨天步行,因此他希望在完成回家这一目标的同时,最小化他步行经过的边的总长度。请你帮助 Yazid 进行计算。 本题的部分测试点将强制在线,具体细节请见【输入格式】和【子任务】。
输入格式
从文件 return.in 中读入数据。 单个测试点中包含多组数据。输入的第一行为一个非负整数 T,表示数据的组数。
接下来依次描述每组数据,对于每组数据:
• 第一行 2 个非负整数 n,m,分别表示节点数、边数。
• 接下来 m 行,每行 4 个正整数 u,v,l,a,描述一条连接节点 u,v 的、长度为 l、海 拔为 a 的边。
– 在这里,我们保证 1≤u,v≤n。
• 接下来一行 3 个非负数 Q,K,S,其中 Q 表示总天数,K ∈{0,1} 是一个会在下面 被用到的系数,S 表示的是可能的最高水位线。
• 接下来 Q 行依次描述每天的状况。每行 2 个整数 v0, p0 描述一天: – 这一天的出发节点为 v = (v0 + K×lastans−1) mod n + 1。
– 这一天的水位线为 p = (p0 + K×lastans) mod (S + 1)。
– 其中 lastans 表示上一天的答案(最小步行总路程)。特别地,我们规定第 1 天时 lastans = 0。
– 在这里,我们保证 1≤v0 ≤n,0≤ p0 ≤S。 对于输入中的每一行,如果该行包含多个数,则用单个空格将它们隔开。
输出格式
输出到文件 return.out 中。 依次输出各组数据的答案。对于每组数据: • 输出 Q 行每行一个整数,依次表示每天的最小步行总路程。
样例:
input
1 4 3 1 2 50 1 2 3 100 2 3 4 50 1 5 0 2 3 0 2 1 4 1 3 1 3 2
output
0 50 200 50 150
解题思路
一.Kruskal重构树
蒟蒻的我看了好长时间。
其实这是一个把边抽象成点的过程。
对于这道题而言,车在没有雨的路径上跑多少是不考虑的,它只要求给出步行最近距离。
而对于步行,我们不需要考虑有没有水。
所以我们只要知道在哪里下车才是最合适的。
所以这道题的思路就是:
1.先跑一边全图Dij,预处理出每一个下车点时到1点的最短路。
2.再跑一遍Kruskal重构树。
3.统计答案。
这里重点说一下Kruskal重构树,网上的讲解好少QAQ
首先我们建一颗最大生成树。
这和普通的建法不太一样。
它使用Kruskal的贪心思想,先将边权排序(从大到小)
在连接的时候将边变成一个新点连进去
这样一颗独立出原图的Kruskal重构树就建出来了。
举个例子,这是原图为了不与边权冲突,以大写字母区分点,字母点为原图具有的,数字点为重构的点。
将边权排序:5 4 3 3 3 2 2 1 1

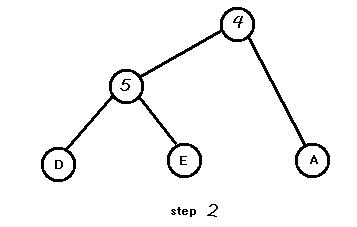
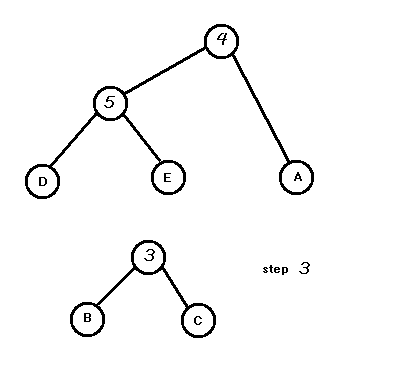
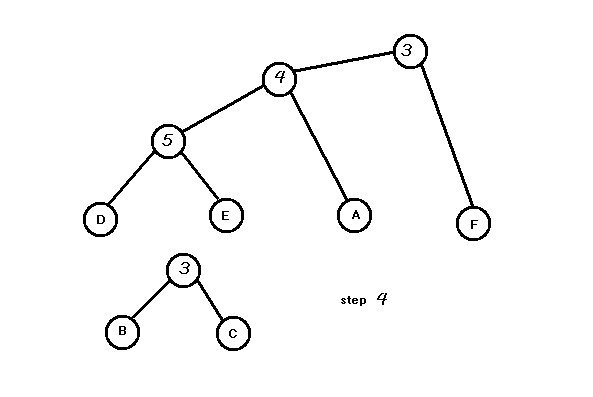
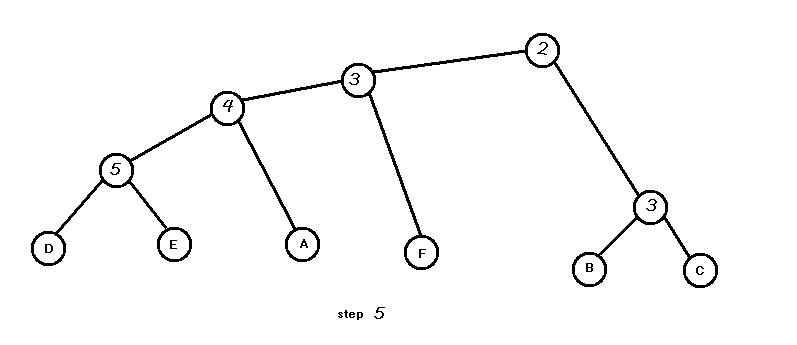
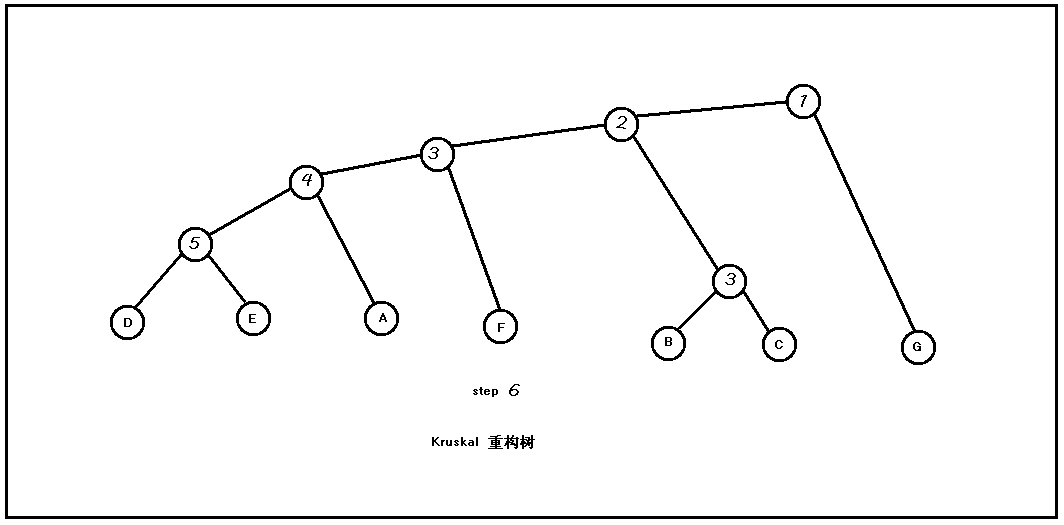
Kruskal重构树是独立出原图的。
构建代码:
void Kruskal() { int tot=n,nm=0; sort(me+1,me+m+1,cmp); for(int i=1;i<=m;i++) { int x=finf(me[i].u); int y=finf(me[i].v); if(x!=y) { nm++; tot++; ade(tot,x); ade(tot,y); p[x].bl=p[y].bl=tot; p[tot].val=me[i].a; p[tot].dis=oo; } if(nm==n-1) break; } Build_dfs(tot,tot); }
它有一些美好的性质:
1.这颗树的重建节点的点权一定大于所有其子树内重建节点点权。 2.非重建节点都是叶节点。 3.这可以由这个图的最大生成树的变形得来,所以具有一些最大生成树的性质
这棵树建好了,然后我们把点权设为边权,然后再记录一下这个点的子树内叶节点的最小距1的距离
很显然越高的节点记录的距1距离越小
好了,每次查询时,使用倍增来得到这个询问点所有父亲祖先上的最小合法点,输出答案即可^_^
代码:
1 #include<queue> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int N=(int)(1e6); 7 const int M=(int)(1e6); 8 const int oo=0x3f3f3f3f; 9 void ads(int f,int t,int v); 10 struct pnt{ 11 int hd; 12 int no; 13 int bl; 14 int fa[20]; 15 int dis; 16 int hdl; 17 int val; 18 bool vis; 19 void rest(int i) 20 { 21 no=i; 22 bl=i; 23 dis=oo; 24 hdl=hd=0; 25 val=0; 26 vis=false; 27 return ; 28 } 29 bool friend operator < (pnt x,pnt y) 30 { 31 return x.dis>y.dis; 32 } 33 }p[N]; 34 struct ede{ 35 int u; 36 int v; 37 int l; 38 int a; 39 void Ins() 40 { 41 scanf("%d%d%d%d",&u,&v,&l,&a); 42 ads(u,v,l); 43 ads(v,u,l); 44 } 45 }me[M]; 46 struct ecc{ 47 int twd; 48 int lst; 49 int vls; 50 }ec[M]; 51 struct ent{ 52 int twd; 53 int lst; 54 }e[N*2]; 55 int T; 56 int cnt; 57 int ect; 58 int n,m; 59 int q,k,s; 60 int lastans; 61 priority_queue<pnt>Q; 62 bool cmp(ede x,ede y) 63 { 64 return x.a>y.a; 65 } 66 void rst() 67 { 68 lastans=0; 69 for(int i=1;i<N;i++) 70 p[i].rest(i); 71 cnt=ect=0; 72 } 73 void ade(int f,int t) 74 { 75 cnt++; 76 e[cnt].twd=t; 77 e[cnt].lst=p[f].hd; 78 p[f].hd=cnt; 79 } 80 void ads(int f,int t,int v) 81 { 82 ect++; 83 ec[ect].twd=t; 84 ec[ect].lst=p[f].hdl; 85 ec[ect].vls=v; 86 p[f].hdl=ect; 87 } 88 int finf(int x) 89 { 90 return x==p[x].bl?x:p[x].bl=finf(p[x].bl); 91 } 92 void Dij() 93 { 94 p[1].dis=0; 95 Q.push(p[1]); 96 while(!Q.empty()) 97 { 98 int x=Q.top().no; 99 Q.pop(); 100 if(p[x].vis)continue; 101 p[x].vis=true; 102 for(int i=p[x].hdl;i;i=ec[i].lst) 103 { 104 int to=ec[i].twd; 105 int vl=ec[i].vls; 106 if(p[to].dis>p[x].dis+vl) 107 { 108 p[to].dis=p[x].dis+vl; 109 Q.push(p[to]); 110 } 111 } 112 } 113 } 114 void Build_dfs(int x,int f) 115 { 116 p[x].fa[0]=f; 117 for(int i=1;i<=19;i++) 118 { 119 p[x].fa[i]=p[p[x].fa[i-1]].fa[i-1]; 120 } 121 for(int i=p[x].hd;i;i=e[i].lst) 122 { 123 int to=e[i].twd; 124 Build_dfs(to,x); 125 p[x].dis=min(p[x].dis,p[to].dis); 126 } 127 } 128 void Kruskal() 129 { 130 int tot=n,nm=0; 131 sort(me+1,me+m+1,cmp); 132 for(int i=1;i<=m;i++) 133 { 134 int x=finf(me[i].u); 135 int y=finf(me[i].v); 136 if(x!=y) 137 { 138 nm++; 139 tot++; 140 ade(tot,x); 141 ade(tot,y); 142 p[x].bl=p[y].bl=tot; 143 p[tot].val=me[i].a; 144 p[tot].dis=oo; 145 } 146 if(nm==n-1) 147 break; 148 } 149 Build_dfs(tot,tot); 150 } 151 int ans(int minpl,int pos) 152 { 153 for(int i=19;~i;i--) 154 if(p[p[pos].fa[i]].val>minpl) 155 pos=p[pos].fa[i]; 156 return p[pos].dis; 157 } 158 int main() 159 { 160 scanf("%d",&T); 161 while(T--) 162 { 163 rst(); 164 scanf("%d%d",&n,&m); 165 for(int i=1;i<=m;i++) 166 me[i].Ins(); 167 Dij(); 168 Kruskal(); 169 scanf("%d%d%d",&q,&k,&s); 170 for(int i=1;i<=q;i++) 171 { 172 int p00,v00; 173 scanf("%d%d",&v00,&p00); 174 v00=(v00+k*lastans-1)%n+1; 175 p00=(p00+k*lastans)%(s+1); 176 lastans=ans(p00,v00); 177 printf("%d\n",lastans); 178 } 179 } 180 return 0; 181 }



