仙人掌的同构(hash)

关于仙人掌的同构，主要是我太蒟蒻了QAQ，问了好几位大佬才弄好。

手撕仙人掌，你得先有手套 ，你得先了解以下基本知识

a.点双连通分量，没什么好说得，仙人掌上有环，判环用点双

b.树的hash点这里

c.仙人掌点这里　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

对于一棵仙人掌，我们通过一些方法来简化:　　　　　　　　　　　　　　　　　

我们最讨厌的是环，假如说没有环，那么树的hash还是蛮简单的。　　　　　　　　　　

OK那么就是圆方树了，如果你还不知道什么是圆方树，请自行百度或者点这里。

当然对于判定仙人掌的同构，不需要一颗完整的圆方树，只需要在环中间建点

 单纯地表示一个环，使用最小表示法（这部分内容我稍后补充QAQ）

单纯地表示一棵树，hash。

嗯，如果你觉得我上面说得十分模糊，那么是正确的，因为还没有开始呢　　^_^

（我其实是不会告诉你我没有用tarjan和完整的圆方树的）

e.g.一个只有一个环的仙人掌

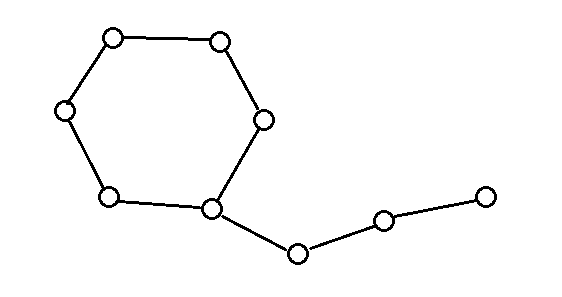
假设我们是这样搜索的

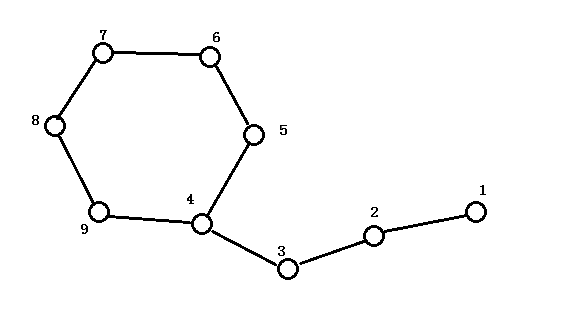
那么在dfs的过程中，要判定一个点在不在环上，记录它的父节点这样在回溯到4时，发现他有一个不是自己儿子的子节点（9）

哈，那就是环的另一端了。

这时抓出9，一直回溯父亲直到4被枚举到，整个环就被揪了出来。

新建一个节点，（在圆方树里则称方点）依次连边。

而对于非环上边直接连就好了

像这样就建立了一个独立出原图的树（一位大佬是这样描述的）

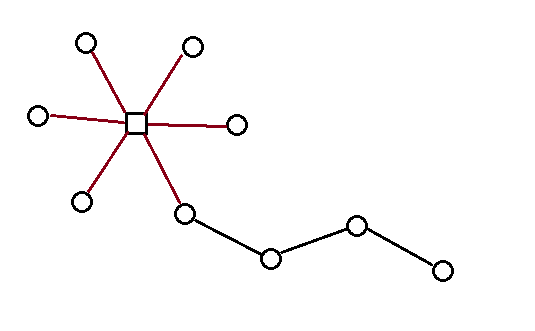
多么优雅的一棵树

好了，现在它是无根的找一下树的重心

新建一个根节点hash一下就好了^_^

你真的觉得这就完了

你太天真了

环是不能这样子搞的

正确打开方式：

别忘了真正的环上点是有顺序的

假如说这个环的方点（中间那个新建点）是根，跑最小表示法（然而我代码里没有这一项QAQ我改天加上）

对于一个普通树节点比如说这样

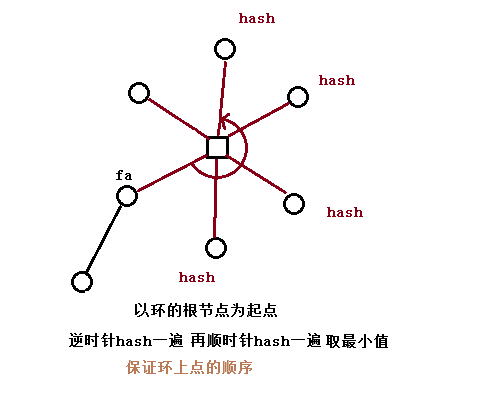
这样就可以了

 代码实现

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef unsigned long long ult;
const ult seed1=1324983271ull;
const ult seed2=4327894239ull;
const ult lth1=9301248721ull;
const ult lth2=8317498371ull;
int nt,mt;
bool cmp(ult x,ult y)
{
    return x<y;
}
struct pnt{
    int hd;
    int sh;
    int fa;
    int wgt;
    bool ong;
    bool vis;
    bool chkd;
    ult has;
};
struct ent{
    int twd;
    int lst;
};
struct Cactus{
    pnt p[300000];
    ent e[500000];
    ent r[500000];
    ult st[1000000];
    int rt[2];
    int n,m;
    int sqn;
    int cnt;
    int cmt;
    void e_ade(int f,int t)
    {
        cnt++;
        e[cnt].twd=t;
        e[cnt].lst=p[f].hd;
        p[f].hd=cnt;
    }
    void r_ade(int f,int t)
    {
        cmt++;
        r[cmt].twd=t;
        r[cmt].lst=p[f].sh;
        p[f].sh=cmt;
    }
    void tr_dfs(int x,int f)
    {
        p[x].vis=true;
        for(int i=p[x].hd;i;i=e[i].lst)
        {
            int to=e[i].twd;
            if((i^f)==1)continue;
            if(!p[to].vis)
            {
                p[to].fa=x;
                p[x].ong=false;
                tr_dfs(to,i);
                if(!p[x].ong)
                {
                    r_ade(x,to);
                    r_ade(to,x);
                }
            }else{
                if(p[to].chkd)continue;
                sqn++;
                int u=x;
                for(u=x;;u=p[u].fa)
                {
                    r_ade(n+sqn,u);
                    r_ade(u,n+sqn);
                    p[u].ong=true;
                    if(u==to)break;
                }
            }
        }
        p[x].chkd=true;
    }
    void gravity(int x,int f)
    {
        p[x].wgt=1;
        bool fl=true;
        for(int i=p[x].sh;i;i=r[i].lst)
        {
            int to=r[i].twd;
            if(to==f)continue;
            gravity(to,x);
            p[x].wgt+=p[to].wgt;
            if(p[to].wgt*2>sqn+n)
                fl=false;
        }
        if((sqn+n-p[x].wgt)*2>sqn+n)
            fl=false;
        if(fl)
        {
            if(rt[0])
            {
                rt[1]=x;
            }else{
                rt[0]=x;
            }
        }
    }
    void Hash(int x,int f)
    {
        int top=0;
        for(int i=p[x].sh;i;i=r[i].lst)
        {
            int to=r[i].twd;
            if(to==f)continue;
            Hash(to,x);
        }
        if(x<=n)
        {
            for(int i=p[x].sh;i;i=r[i].lst)
            {
                int to=r[i].twd;
                if(to==f)continue;
                st[++top]=p[to].has;
            }
            sort(st+1,st+top+1,cmp);
            p[x].has=seed1;
            for(int i=1;i<=top;i++)
            {
                p[x].has=((p[x].has*lth1+st[i])^st[i])+st[i];
            }
        }else{
            int i;
            for(i=p[x].sh;i;i=r[i].lst)
            {
                if(r[i].twd==f)
                    break;
            }
            for(i=r[i].lst;i;i=r[i].lst)
            {
                int to=r[i].twd;
                st[++top]=p[to].has;
            }
            for(i=p[x].sh;i;i=r[i].lst)
            {
                int to=r[i].twd;
                if(to==f)
                    break;
                st[++top]=p[to].has;
            }
            ult tmp1=seed2,tmp2=seed2;
            for(i=1;i<=top;i++)
            {
                tmp1=((tmp1*lth2+st[i])^st[i])+st[i];
            }
            for(i=top;i;i--)
            {
                tmp2=((tmp2*lth2+st[i])^st[i])+st[i];
            }
            p[x].has=min(tmp1,tmp2);
            p[x].has*=lth2;
        }
    }
    ult solve(int nn,int mm)
    {
        n=nn;
        m=mm;
        cnt=1;
        for(int i=1;i<=m;i++)
        {
            int x;
            int y;
            scanf("%d%d",&x,&y);
            e_ade(x,y);
            e_ade(y,x);
        }
        tr_dfs(1,0);
        gravity(1,0);
        r_ade(0,rt[0]);
        if(rt[1])
        {
            r_ade(0,rt[1]);
            for(int i=p[rt[0]].sh;i;i=r[i].lst)
            {
                if(r[i].twd==rt[1])
                    r[i].twd=0;
            }
            for(int i=p[rt[1]].sh;i;i=r[i].lst)
            {
                if(r[i].twd==rt[0])
                    r[i].twd=0;
            }
        }
        Hash(0,0);
        return p[0].has;
    }
}C[2];
int main()
{
    scanf("%d%d",&nt,&mt);
    if(C[0].solve(nt,mt)==C[1].solve(nt,mt))
    {
        printf("YES\n");
    }else{
        printf("NO\n");
    }
    return 0;
}

大概就是这样了^_^