IOIOI卡片占卜(Atcoder-IOIOI カード占い)（最短路）

题目描述：

K 理事長は占いが好きで，いつも様々な占いをしている．今日は，表の面に ‘I’ が，裏の面に ‘O’ が書か れたカードを使って今年の IOI での日本選手団の出来を占うことにした． 占いの方法は次のようなものである．

1. まず，正の整数 A, B,C, D, E を決める．

2. A + B + C + D + E 枚のカードを横 1 列に並べる．このとき，左から A 枚は表，続く B 枚は裏，続く C 枚は表，続く D 枚は裏，続く E 枚は表にして並べる．このように並べると，左から順に ‘I’ が A 個，‘O’ が B 個，‘I’ が C 個，‘O’ が D 個，‘I’ が E 個並ぶことになる．

3. あらかじめ決められた N 種類の操作の中から 1 つ以上の操作を選び，好きな順番で行う．このとき， 同じ種類の操作を 2 回以上行っても良い．i (1 ≦ i ≦ N) 種類目の操作は「左から Li 枚目から Ri 枚目 までのカードの表裏をすべてひっくり返す」というものである．1 枚のカードをひっくり返すのに 1 秒かかる．したがって，i 種類目の操作を行うには，Ri − Li + 1 秒かかる． 4. 操作が終わった後，すべてのカードが表になっていれば占いは成功となる． K 理事長は必要以上にカードをひっくり返すことを避けるために，カードを実際に使って占う前にまず， 占いを成功させることが可能なのかどうかを求めることにした．さらに，もし占いを成功させることが可 能な場合は，占いを成功させるためにかかる時間の最小値を求めることにした．

課題 カードの並べ方の情報と，あらかじめ決められた操作の情報が与えられる．占いを成功させることが可 能かどうかを求め，可能である場合は占いを成功させるためにかかる時間の最小値を求めるプログラムを 作成せよ．

 

K理事长很喜欢占卜，经常用各种各样的方式进行占卜。今天，他准备使用正面写着”I”，反面写着”O”的卡片为今年IOI的日本代表队占卜最终的成绩。

占卜的方法如下所示：

1.首先，选择5个正整数A,B,C,D,E。

2.将A+B+C+D+E张IOI卡片排成一行，最左侧的A张卡片正面朝上，接下来B张反面朝上，接下来C张卡片正面朝上，接下来D张反面朝上，最后E张正面朝上。如此排列的话，从左侧开始顺次为A张“I”，B张“O”，C张“I”，D张“O”，E张“I”。

3.在预先决定的N种操作中选出至少1种，然后按照任意顺序执行。(注：同种操作执行多次也是可以的。)这里，第i种操作(1<=i<=N)为【将从左数第Li张卡片到第Ri张卡片全部翻转】。翻转一张卡片需要1秒的时间，因此第i种操作耗时Ri-Li+1秒。

4.操作结束后，如果所有卡片都是正面朝上则占卜成功。

K理事长不想翻多余的牌，因此在实际使用卡片占卜之前会先计算出是否存在占卜成功的可能性。进一步，如果占卜可能成功，他会计算出能使占卜成功所消耗的时间的最小值。

现在给出卡片的排列信息和预先决定的操作信息，请你写一个程序，计算出占卜能否成功，如果能成功，输出消耗时间的最小值。

【Input】

第一行5个空格分隔的整数A,B,C,D,E，表示占卜初始时，从最左端开始依次是A枚正面朝上，接下来B枚背面朝上，接下来C枚正面朝上，接下来D枚背面朝上，最后E枚正面朝上。

接下来一行一个正整数N，表示预先决定的操作种类数。

接下来N行，第i行(1<=i<=N)两个空格分隔的正整数Li，Ri，表示第i种操作为【将从左数第Li张卡片到第Ri张卡片全部翻转】。

【Output】

如果占卜能够成功，输出消耗时间的最小值，否则输出-1。

【Sample Input】

1 2 3 4 5

3

2 3

2 6

4 10

 

【Sample Output】

12

 

【HINT】

 

初始的卡片序列为IOOIIIOOOOIIIII。

 

执行第2种操作后得到IIIOOOOOOOIIIII，耗时5秒。

 

接下来执行第3中操作，得到IIIIIIIIIIIIIII，占卜成功，耗时7秒。

 

耗时12秒完成占卜，这是耗时的最小值，故输出12。

 

【Data Constraint】

对于15%的数据，N<=10

对于另外50%的数据，1<=A,B,C,D,E<=50

对于100%的数据：

1<=A,B,C,D,E,N<=10^5

1<=Li<=Ri<=A+B+C+D+E (1<=i<=N)

洛谷题目

乍一看感觉题目没有什么头绪，但仔细思考，好像你只需要让反面朝上的卡牌翻动奇数次，让正面朝上的卡牌翻动偶数次即可。（一句废话）

那么，对于01交界处一定有翻动，因为两侧翻动次数一定不相同。

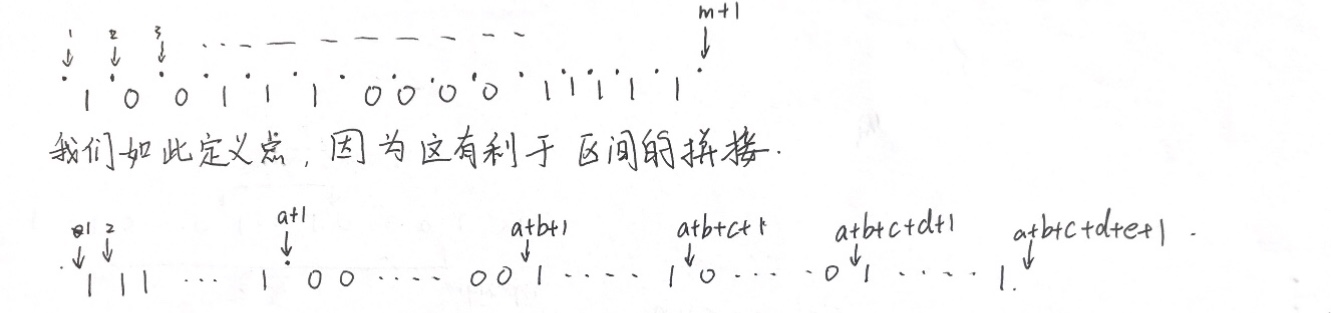
如果一个区间不够长，那么我们考虑接下去：

　　比如说，像这样，一个区间(我们称之区间A)的左端点[i1]正好在[a+1]处而它的右端点小于[a+b]，那么它一定不能完成整个区间(就是从a+1到a+b)的翻转。考虑接下去，如果这时恰好有一个区间(我们称之区间B)的左端点就是A的右端点，那么就是说：它可以这么一直接下去直到到达[a+b+1]。

当然这只是最理想的情况，事实上，这其实给我们提供了一个思路:你看啊，怎么实现区间的拼接呢，有没有想到一个叫做图论的东西：比如说我们把一个区间的两端作为点，而边权就是这个区间反转的长度，正好是这个区间右端点的值减去左端点的。

而翻转奇数次的点一定在起始点区间内

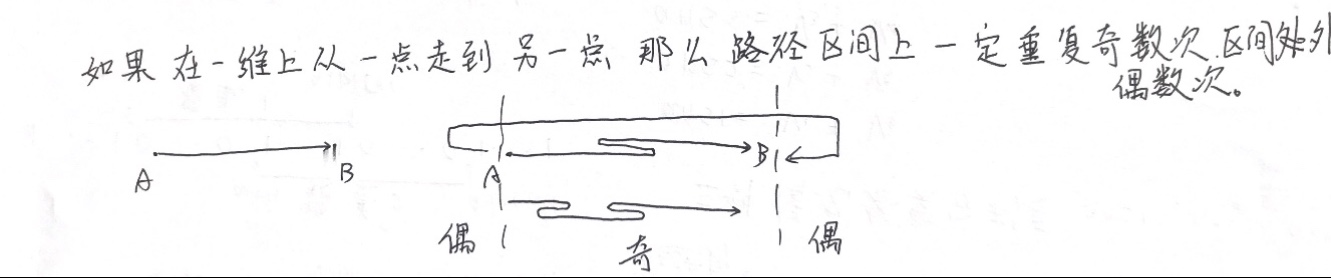
神奇不是吗

那么我们就要考虑一下了，如果已经建好了边，边权还是反转的次数，而题目问的是最少翻转次数，

那这不就是最短路吗

是不是很神奇

好了，那么，怎么构造呢

无非就是这三种情况：

 

嗯，那就是这样了

/代码具体实现如下

#include<queue>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long lnt;
struct pnt{
    int hd;
    int no;
    lnt dis;
    bool vis;
    bool friend operator < (pnt x,pnt y)
    {
        return x.dis>y.dis;
    }
}p[500005];
struct ent{
    int twd;
    int lst;
    lnt vls;
}e[200005];
int a,b,c,d,jdr;
int n,m;
int piq[10000];
int cnt;
lnt ans1,ans2,ans3;
priority_queue<pnt>Q;
void ade(int f,int t,lnt v)
{
    cnt++;
    e[cnt].twd=t;
    e[cnt].vls=v;
    e[cnt].lst=p[f].hd;
    p[f].hd=cnt;
}
int main()
{
    scanf("%d%d%d%d%d%d",&a,&b,&c,&d,&jdr,&n);
    m=a+b+c+d+jdr;
    for(int i=1;i<=n;i++)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        ade(l,r+1,(lnt)(r-l+1));
        ade(r+1,l,(lnt)(r-l+1));
    }
    for(int i=1;i<=m+1;i++)
    {
        p[i].dis=0x3f3f3f3f3f3f3f3fll;
        p[i].vis=0;
        p[i].no=i;
    }
    p[a+1].dis=0;
    Q.push(p[a+1]);
    while(!Q.empty())
    {
        int x=Q.top().no;
        Q.pop();
        if(p[x].vis)continue;
        p[x].vis=1;
        for(int i=p[x].hd;i;i=e[i].lst)
        {
            int to=e[i].twd;
            if(p[to].dis>p[x].dis+e[i].vls)
            {
                p[to].dis=p[x].dis+e[i].vls;
                Q.push(p[to]);
            }
        }
    }
    ans1+=(lnt)p[a+b+1].dis;
    ans2+=(lnt)p[a+b+c+1].dis;
    ans3+=(lnt)p[a+b+c+d+1].dis;
    for(int i=1;i<=m+1;i++)
    {
        p[i].dis=0x3f3f3f3f3f3f3f3fll;
        p[i].vis=0;
        p[i].no=i;
    }
    p[a+b+1].dis=0;
    Q.push(p[a+b+1]);
    while(!Q.empty())
    {
        int x=Q.top().no;
        Q.pop();
        if(p[x].vis)continue;
        p[x].vis=1;
        for(int i=p[x].hd;i;i=e[i].lst)
        {
            int to=e[i].twd;
            if(p[to].dis>p[x].dis+e[i].vls)
            {
                p[to].dis=p[x].dis+e[i].vls;
                Q.push(p[to]);
            }
        }
    }
    ans2+=(lnt)p[a+b+c+d+1].dis;
    ans3+=(lnt)p[a+b+c+1].dis;
    for(int i=1;i<=m+1;i++)
    {
        p[i].dis=0x3f3f3f3f3f3f3f3fll;
        p[i].vis=0;
        p[i].no=i;
    }
    p[a+b+c+1].dis=0;
    Q.push(p[a+b+c+1]);
    while(!Q.empty())
    {
        int x=Q.top().no;
        Q.pop();
        if(p[x].vis)continue;
        p[x].vis=1;
        for(int i=p[x].hd;i;i=e[i].lst)
        {
            int to=e[i].twd;
            if(p[to].dis>p[x].dis+e[i].vls)
            {
                p[to].dis=p[x].dis+e[i].vls;
                Q.push(p[to]);
            }
        }
    }
    ans1+=(lnt)p[a+b+c+d+1].dis;
    lnt ans=min(ans1,min(ans2,ans3));
    if(ans>=0x3f3f3f3f3f3f3f3fll)
        printf("-1\n");
    else
        printf("%lld\n",ans);
    return 0;
}