【DP】Educational Codeforces Round 123 (Rated for Div. 2)

前言

本场链接：Educational Codeforces Round 123 (Rated for Div. 2)

A、B题目本身不难，但是却有很多做法；C题属于DP，是我不熟悉的类型（基本不会），比较难，但好在看了题解后大致明白了。

A-Doors and Keys

题目

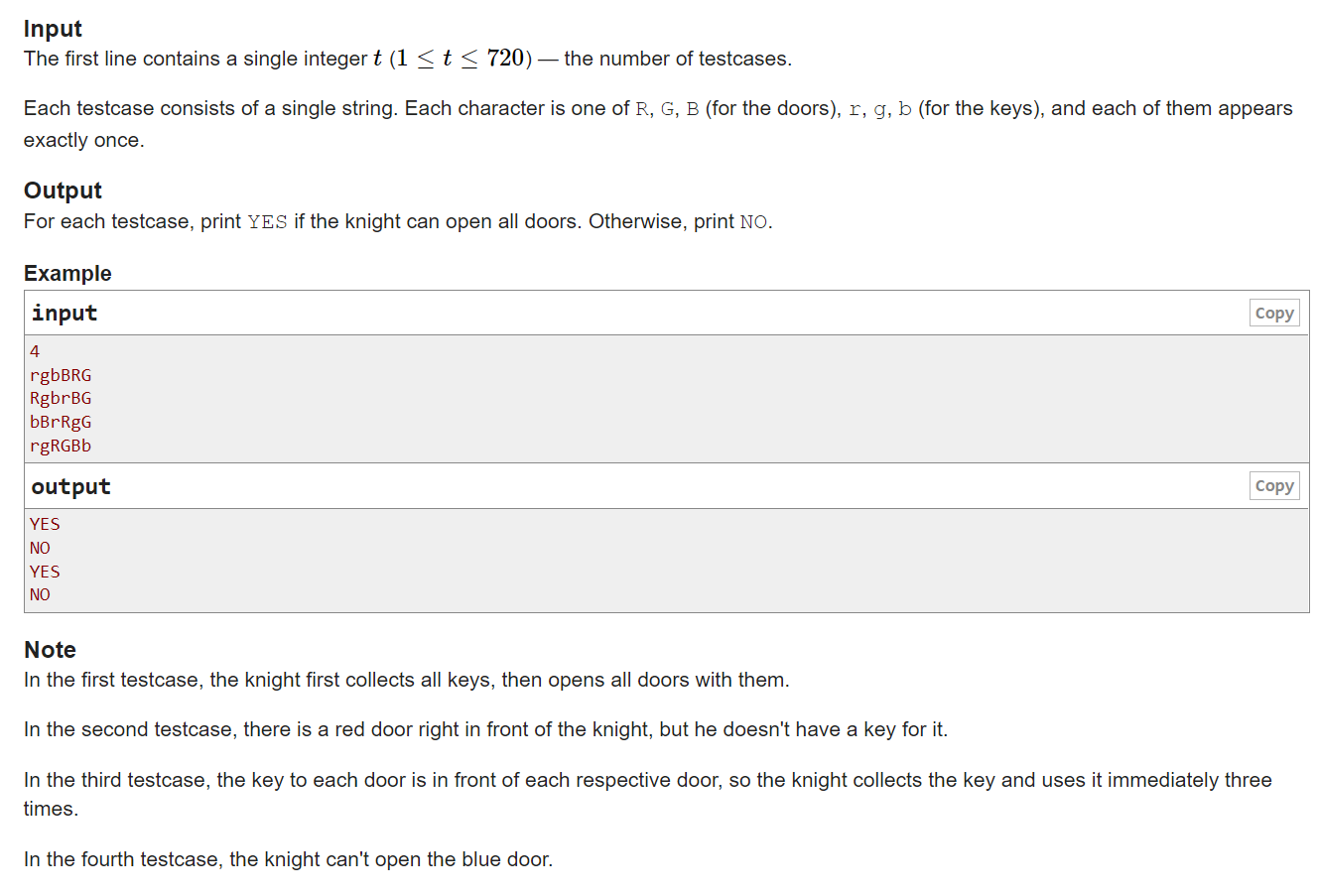
The knight is standing in front of a long and narrow hallway. A princess is waiting at the end of it.

In a hallway there are three doors: a red door, a green door and a blue door. The doors are placed one after another, however, possibly in a different order. To proceed to the next door, the knight must first open the door before.

Each door can be only opened with a key of the corresponding color. So three keys: a red key, a green key and a blue key — are also placed somewhere in the hallway. To open the door, the knight should first pick up the key of its color.

The knight has a map of the hallway. It can be transcribed as a string, consisting of six characters:

• R, G, B — denoting red, green and blue doors, respectively;
• r, g, b — denoting red, green and blue keys, respectively.

Each of these six characters appears in the string exactly once.

The knight is standing at the beginning of the hallway — on the left on the map.

Given a map of the hallway, determine if the knight can open all doors and meet the princess at the end of the hallway.

解法一（SET容器判断存在）

思想

本质上是利用STL的 count(x) 函数，此函数会返回容器中x元素的数量，但因为set中的同一元素只能存在1个，所以当x存在时， count(x) 返回1，否则返回0。

遍历字符串，如果当前门前面出现过该门的钥匙，就可以通过。

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <set>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        string s;
        cin >> s;
        set<int> vis;
        int fl = 1;
        for (auto x : s) {
            if ('a' <= x && x <= 'z') {
                vis.insert(x - 'a');
            } else {
                fl = fl && vis.count(x - 'A');
            }
        }
        if (fl)
            cout << "YES\n";
        else
            cout << "NO\n";
    }
    return 0;
}

解法二（string中的find()函数）

思想

因为每种门和钥匙出现且只会出现一次，所以如果钥匙出现在该门的后面，那就无法开门。

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        string s;
        cin >> s;
        int flag = 1;
        for (int i = 0; i < s.size(); ++i) {
            if (s[i] >= 'A' && s[i] <= 'Z') {
                if (s.find(tolower(s[i])) > i) {
                    flag = 0;
                    break;
                }
            }
        }
        if (flag)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

解法三（纯纯的浪费时间）

思想

没有思想

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        string s;
        cin >> s;
        ll r = 0, g = 0, b = 0;
        int flag = 1;
        for (auto x : s) {
            if (x >= 'a' && x <= 'z') {
                if (x == 'r')
                    r++;
                else if (x == 'g')
                    g++;
                else
                    b++;
            } else {
                if (x == 'R') {
                    if (r > 0)
                        r--;
                    else {
                        flag = 0;
                        break;
                    }
                } else if (x == 'G') {
                    if (g > 0)
                        g--;
                    else {
                        flag = 0;
                        break;
                    }
                } else {
                    if (b > 0)
                        b--;
                    else {
                        flag = 0;
                        break;
                    }
                }
            }
        }
        if (flag)
            cout << "YES" << endl;
        else
            cout << "NO" << endl;
    }
    return 0;
}

B-Anti-Fibonacci Permutation

题目

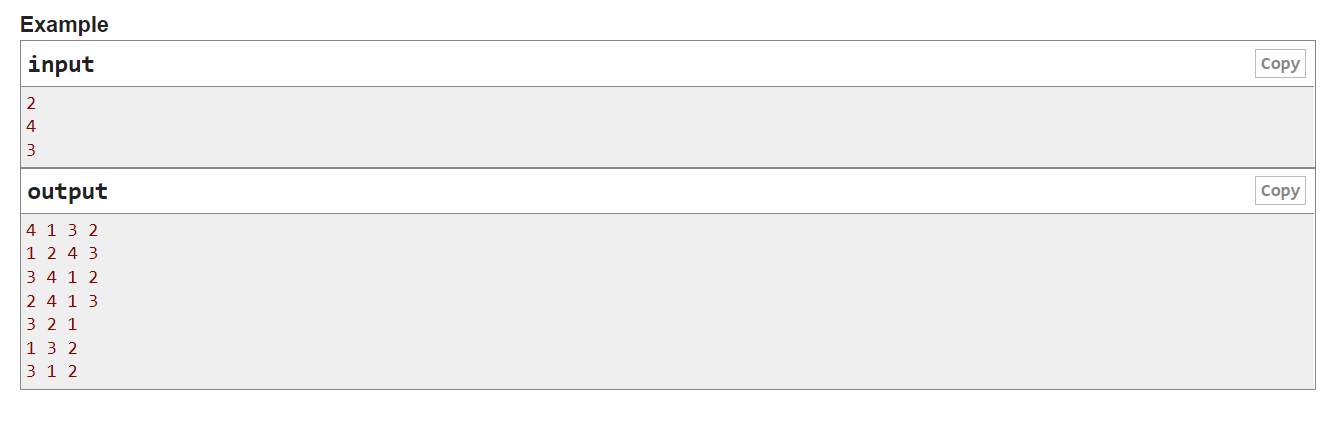
Let's call a permutation pp of length nn anti-Fibonacci if the condition pi−2+pi−1≠pipi−2+pi−1≠pi holds for all ii (3≤i≤n3≤i≤n). Recall that the permutation is the array of length nn which contains each integer from 11 to nn exactly once.

思想

其实只要尽量让这个排列呈递减状态就好了，因为斐波那契数列是递增的。

但我是用全排列加检验的方法。

代码1（简单）

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        for (int i = 1; i <= n; ++i) {
            cout << i;
            for (int j = n; j >= 1; --j) {
                if (i == j) continue;
                cout << " " << j;
            }
            cout << endl;
        }
    }
    return 0;
}

代码2（较复杂）

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        int n;
        cin >> n;
        vector<ll> p(n);
        int t = 0;
        for (auto& x : p) x = ++t;
        int cnt = 0;
        do {
            int flag = 1;
            for (int i = 2; i < n; ++i) {
                if (p[i - 1] + p[i - 2] == p[i]) {
                    swap(p[i], p[i - 1]);
                }
            }
            if (flag) {
                cnt++;
                for (auto x : p) cout << x << " ";
                cout << endl;
            }
            if (cnt == n) break;
        } while (next_permutation(p.begin(), p.end()));
    }
    return 0;
}

C-Increase Subarray Sums

题目

You are given an array a1,a2,…,ana1,a2,…,an, consisting of nn integers. You are also given an integer value xx.

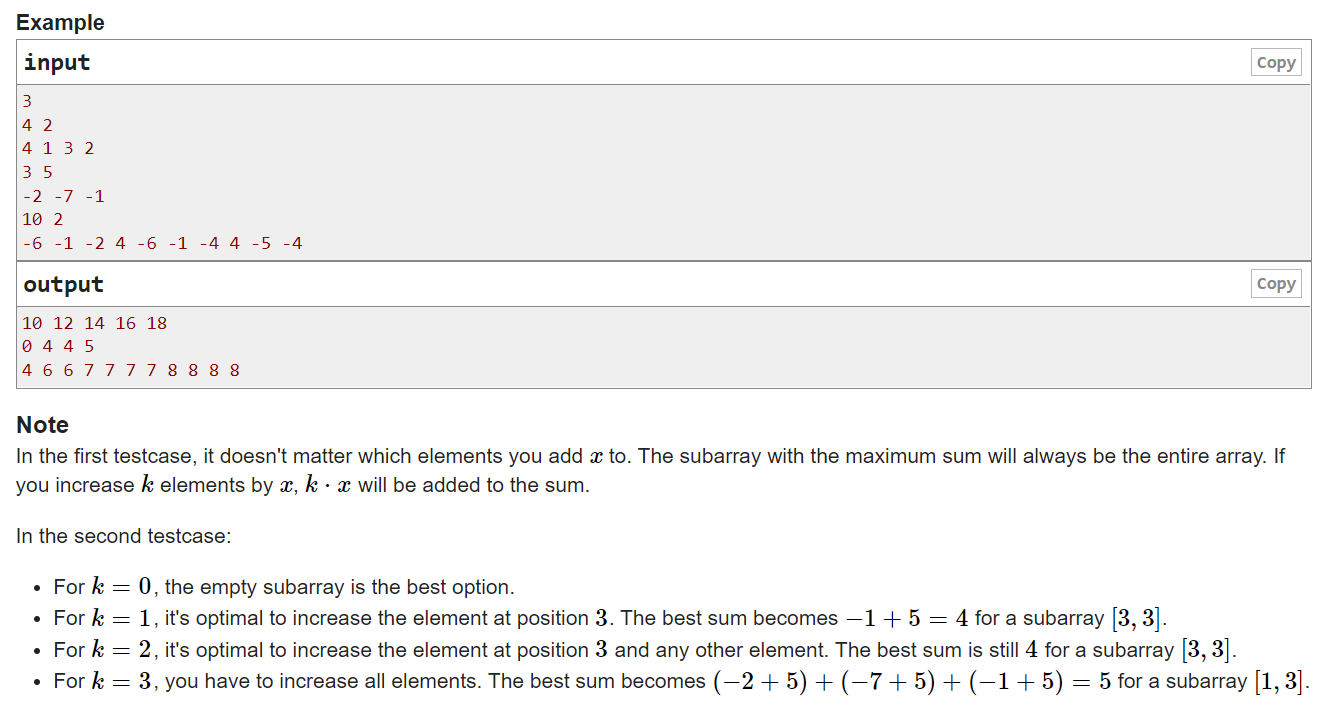
Let f(k)f(k) be the maximum sum of a contiguous subarray of aa after applying the following operation: add xx to the elements on exactly kk distinct positions. An empty subarray should also be considered, it has sum 00.

Note that the subarray doesn't have to include all of the increased elements.

Calculate the maximum value of f(k)f(k) for all kk from 00 to nn independently.

思想

DP的思路。

本质上是用DP求最大子数组和，根据题意稍加修改即可。

注意

1、dp[i]数组表示的是以第 i 位为子数组尾的最大子数组和。

2、dp[] 和 new_dp[] 其实就是一个二维的dp数组，用来滚动的。

3、res[i] 表示的是最多取 i 个数加上 x 后的最大子数组和。

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
    SF;
    int T;
    cin >> T;
    while (T--) {
        int n, x;
        cin >> n >> x;
        vector<ll> a(n + 1);
        for (int i = 1; i <= n; ++i) cin >> a[i];
        vector<ll> dp(n + 1, max(a[1] + x, 0LL)), res;
        dp[0] = max(a[1], 0LL);
        res = dp;
        for (int i = 2; i <= n; ++i) {
            vector<ll> new_dp(n + 1, 0);
            for (int j = 0; j <= n; ++j) {
                new_dp[j] = max(dp[j] + a[i], new_dp[j]);
                if (j > 0) {
                    new_dp[j] = max(dp[j - 1] + a[i] + x, new_dp[j]);
                }
                res[j] = max(new_dp[j], res[j]);
            }
            dp = new_dp;
        }
        for (int i = 0; i <= n; ++i) {
            cout << res[i] << " ";
        }
        cout << endl;
    }
    return 0;
}