2022GDUT寒假专题学习-4 数论

前言

专题链接：2022_GDUT_新生专题训练_数论 - Virtual Judge (vjudge.net)

数论专题算是比较难的专题了，对于刚入门的新手来说，这么多数学公式属实不太好理解，但好在搞懂了之后就不会太难了。

A - k-rounding

题目

For a given positive integer n denote its k-rounding as the minimum positive integer x, such that x ends with k or more zeros in base 10 and is divisible by n.

For example, 4-rounding of 375 is 375·80 = 30000. 30000 is the minimum integer such that it ends with 4 or more zeros and is divisible by 375.

Write a program that will perform the k-rounding of n.

思想

只需要求 n 和 1ek 的最小公倍数就行了

代码

#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
ll gcd(ll a, ll b) {
    if (b == 0) return a;
    return gcd(b, a % b);
}
int main() {
    SF ll n, k;
    cin >> n >> k;
    ll p = pow(10, k);
    ll l = n * p / gcd(n, p);
    cout << l << endl;
    return 0;
}

E - Prime Distance

题目

The branch of mathematics called number theory is about properties of numbers. One of the areas that has captured the interest of number theoreticians for thousands of years is the question of primality. A prime number is a number that is has no proper factors (it is only evenly divisible by 1 and itself). The first prime numbers are 2,3,5,7 but they quickly become less frequent. One of the interesting questions is how dense they are in various ranges. Adjacent primes are two numbers that are both primes, but there are no other prime numbers between the adjacent primes. For example, 2,3 are the only adjacent primes that are also adjacent numbers.
Your program is given 2 numbers: L and U (1<=L< U<=2,147,483,647), and you are to find the two adjacent primes C1 and C2 (L<=C1< C2<=U) that are closest (i.e. C2-C1 is the minimum). If there are other pairs that are the same distance apart, use the first pair. You are also to find the two adjacent primes D1 and D2 (L<=D1< D2<=U) where D1 and D2 are as distant from each other as possible (again choosing the first pair if there is a tie).

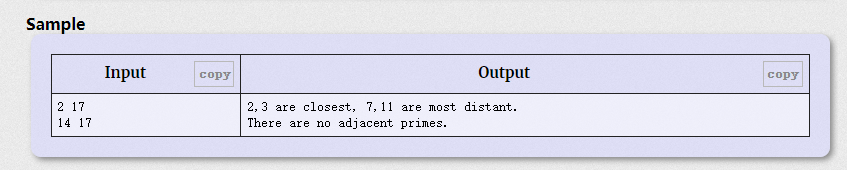
思想

此题主要是考察如何快速查找大数区间内的素数

因为 L，R 范围过大，无法直接用vis桶来标记合数，但又因为 R - L 最大只到1e6，所以我们只需要给这个区间内的数加一个大小为L的左偏移量就可以了！

筛质数的方法还是用埃氏筛就行了

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <set>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const ll inf = 0x3f3f3f3f;
const ll N = 1e6 + 10;
ll zs[N], vis[N];
vector<ll> zsss;
ll zss(ll n) {
    bool flag = 1;
    if (n == 0 || n == 1) return 0;
    for (ll i = 0; i < zsss.size(); ++i) {
        if (zsss[i] * zsss[i] > n) break;
        if (n % zsss[i] == 0) {
            flag = 0;
            break;
        }
    }
    return flag;
}
int main() {
    SF zs[0] = zs[1] = 1;
    for (ll i = 2; i <= 50000; ++i) {
        if (zs[i] == 0) {
            zsss.push_back(i);
            for (ll j = i * i; j <= 50000; j += i) zs[j] = 1;
        }
    }
    ll l, r;
    while (cin >> l >> r) {
        if (l == 1) l = 2;
        ll flag = 0;
        for (int i = 0; i < zsss.size(); ++i) {
            ll a, b;
            a = max(l / zsss[i] - 1, 2LL);
            b = r / zsss[i];
            for (ll j = a; j <= b; ++j) {
                if (j * zsss[i] >= l && j * zsss[i] <= r) {
                    vis[j * zsss[i] - l] = 1;
                }
            }
        }
        ll minl = 0, minr = 0, maxl = 0, maxr = 0, mind = inf, maxd = -1, tl = -1, tr = -1;
        for (ll i = 0; i <= r - l; ++i) {
            if (vis[i] == 0) {
                flag++;
                if (tl == -1)
                    tl = i;
                else {
                    tr = i;
                    if (tr - tl < mind) {
                        mind = tr - tl;
                        minl = tl + l, minr = tr + l;
                    }
                    if (tr - tl > maxd) {
                        maxd = tr - tl;
                        maxl = tl + l, maxr = tr + l;
                    }
                    tl = tr;
                }
            } else
                vis[i] = 0;
        }
        if (flag <= 1) {
            cout << "There are no adjacent primes." << endl;
        } else
            cout << minl << "," << minr << " are closest, " << maxl << "," << maxr << " are most distant." << endl;
    }
    return 0;
}

G - 青蛙的约会

题目

artist 和 小旋 只在网上一起打过比赛，没有见过面。

开学返校了，他们决定出来约个饭 ，他们处于同一条长为L的轴线上，且这条轴线是头尾相连的

artist的初始坐标是X ， 她顺时针走，每秒可以走m米

小旋的初始坐标是Y ， 他也是顺时针走，每秒可以走n米

小旋和artist每秒都在走路。小旋想知道，他到底要走多少秒，才能遇见artist呢？

秒只能是整数秒，遇见的含义是到同一个坐标。

注意：这道题不支持bits/stdc++.h头文件！

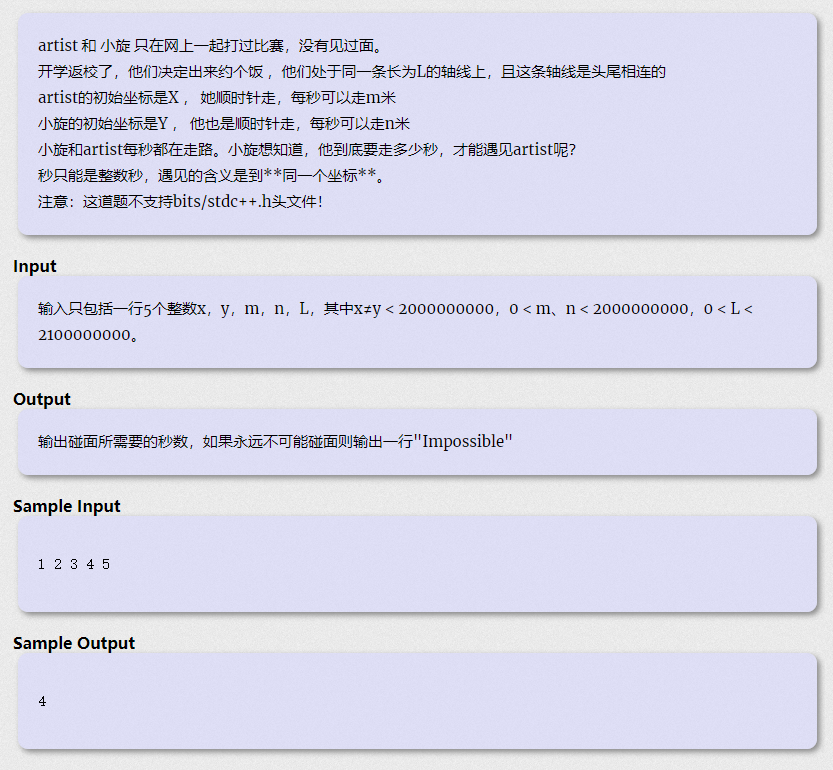
思想

考察扩展欧几里得的使用

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, y, x);
    y -= (a / b) * x;
    return d;
}
int main() {
    SF;
    ll x, y, m, n, l, dist;
    cin >> x >> y >> m >> n >> l;
    ll a = m - n, c = y - x;
    if (a < 0) a = -a, c = -c;
    ll tx, ty, d;
    d = exgcd(a, l, tx, ty);
    tx = (tx * (c / d)) % (l / d);
    tx = (tx + l / d) % (l / d);
    if (c % d == 0)
        cout << tx << endl;
    else
        cout << "Impossible" << endl;
    return 0;
}