【二进制枚举】2022牛客寒假集训5 C-战旗小孩

C - 战棋小孩

题目来源：2022牛客寒假算法基础集训营5

题目链接：C-战棋小孩_2022牛客寒假算法基础集训营5 (nowcoder.com)

题目

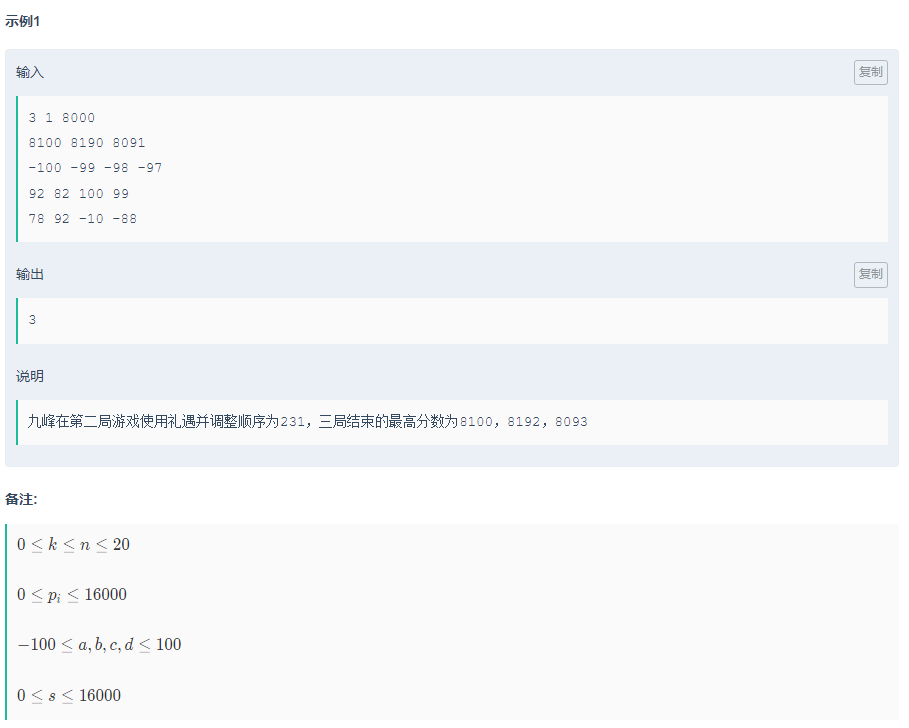
酒馆战棋排行榜记录了全国积分最高的200个账号,上榜是九峰的梦想。
这一天九峰进行了nnn局游戏,每局游戏都可以从两个英雄中选择一位，由于九峰的发挥过于稳定，所以他的游戏结果只与选择英雄的强度相关，并且九峰手中有若干次礼遇的机会，使用后能使得本局游戏能额外多出两个英雄可以选择，但礼遇只能在选择前使用，也就是说九峰不能在看见两个可选英雄后再考虑是否使用礼遇。
每局游戏后九峰都会看一眼排行榜，如果他上榜了就会很开心。
九峰想上榜的欲望过于强烈以至于打动了时空之神，神给与了他自由排列游戏顺序的能力
现在给出每局游戏的选将情况和结束后上榜需要的分数，和每局游戏结束后,排行榜上需要的分数，九峰想知道通过能力合理排列并进行最优选择后，他最多因上榜而开心的次数。

思想

主要算法：贪心 + 二进制枚举

首先不难发现，要想上榜次数最多，肯定是加的分越快越好（快的意思是，优先进行分数最高的场）。

但因为使用礼遇的局次无法确定（总之就是很复杂），所以使用二进制将每一种情况枚举出来，选出上榜次数最多的一种情况就好了！

代码

#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int n, k, s;
int p[50], v[50], w[50], fin[50];
int popcount(ll x) {
    int cnt = 0;
    while (x) {
        if (x & 1) cnt++;
        x >>= 1;
    }
    return cnt;
}
int cal(int x) {
    for (int i = 0; i < n; ++i) {
        if (x >> i & 1)
            fin[i + 1] = w[i + 1];
        else
            fin[i + 1] = v[i + 1];
    }
    sort(fin + 1, fin + 1 + n, greater<int>());
    int res = s, cnt = 0;
    for (int i = 1; i <= n; ++i) {
        res += fin[i];
        if (res >= p[i]) cnt++;
    }
    return cnt;
}
int main() {
    SF;
    cin >> n >> k >> s;
    for (int i = 1; i <= n; ++i) cin >> p[i];
    for (int i = 1, a, b, c, d; i <= n; ++i) {
        cin >> a >> b >> c >> d;
        v[i] = max(a, b);
        w[i] = max(v[i], max(c, d));
    }
    int mx = 1 << n, ans = -inf;
    for (int i = 0; i < mx; ++i) {
        if (popcount(i) == k) ans = max(ans, cal(i));
    }
    cout << ans << endl;
    return 0;
}