2022牛客寒假集训4 J-区间合数的最小公倍数

J-区间合数的最小公倍数

题目来源：2022牛客寒假算法基础集训营4

题目链接：J-区间合数的最小公倍数_2022牛客寒假算法基础集训营4 (nowcoder.com)

题目

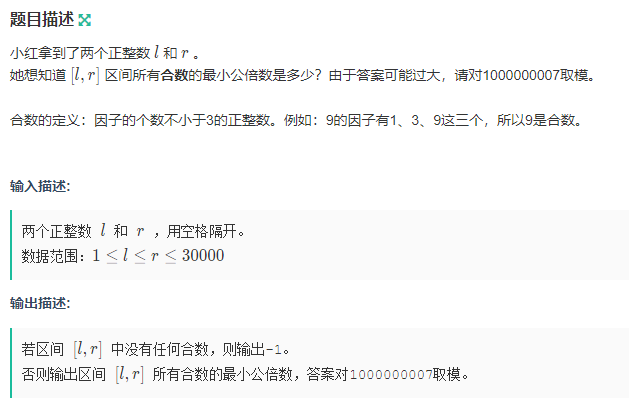
小红拿到了两个正整数 lll 和 rrr 。

她想知道 [l,r][l,r][l,r] 区间所有合数的最小公倍数是多少？由于答案可能过大，请对1000000007取模。

合数的定义：因子的个数不小于3的正整数。例如：9的因子有1、3、9这三个，所以9是合数。

思想

一般求多个数的最小公倍数有两种求法：

1、（较方便常用，但在本题的模意义下不适用）先求两个数的最小公倍数，再接着往后一个个求。

2、（本题适用）对每个数分解质因数，找出每个出现过的质数的最高次幂，将他们乘起来就是最小公倍数了。

接下来细说第二种求法：

例如求 6 8 9 10 的 最小公倍数

6 = 2 * 3

8 = 2 * 2 * 2 = 2^3

9 = 3 * 3 = 3^2

10 = 2 * 5

所以 最小公倍数 = 2^3（来自8）* 3^2（来自9）*5（来自10）

代码

#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <set>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const ll p = 1000000007;
const int inf = 0x3f3f3f3f;
const int N = 3e4 + 10;
ll hs[N], num[N];
set<int> zs;  //存质数
int main() {
    SF;
    ll l, r;
    cin >> l >> r;
    hs[0] = hs[1] = hs[2] = hs[3] = 0;
    for (int i = 2; i <= r; ++i) {
        if (hs[i] == 0) {
            for (int j = i + i; j <= r; j += i) {
                hs[j] = 1;
            }
            zs.insert(i);  //压质数
        }
    }
    bool flag = 1;
    for (int i = l; i <= r; ++i) {
        if (hs[i] == 1) {
            flag = 0;
            ll tot = 0, id;
            for (auto x : zs) {  //分解质因数
                ll t = i, cnt = 0;
                while (t) {
                    if (t % x == 0)
                        cnt++;
                    else
                        break;
                    t /= x;
                }
                if (cnt > num[x]) num[x] = cnt;  //如果当前质数的幂比所存的大，就更新成当前的
            }
        }
    }
    ll ans = 1;
    for (int i = 1; i <= r; ++i) {
        if (num[i] != 0) {
            ll c = 1;
            for (int j = 1; j <= num[i]; ++j) c = c * i % p;
            ans = ans * c % p;
        }
    }
    if (flag)
        cout << -1 << endl;
    else
        cout << ans << endl;
    return 0;
}