2022GDUT寒假专题学习-3 图论

专题链接：专题训练3-图论 - Virtual Judge (vjudge.net)

A - 并查集

题目

这是一道模板题。

维护一个 nn 点的无向图，支持：

• 加入一条连接 uu 和 vv 的无向边
• 查询 uu 和 vv 的连通性

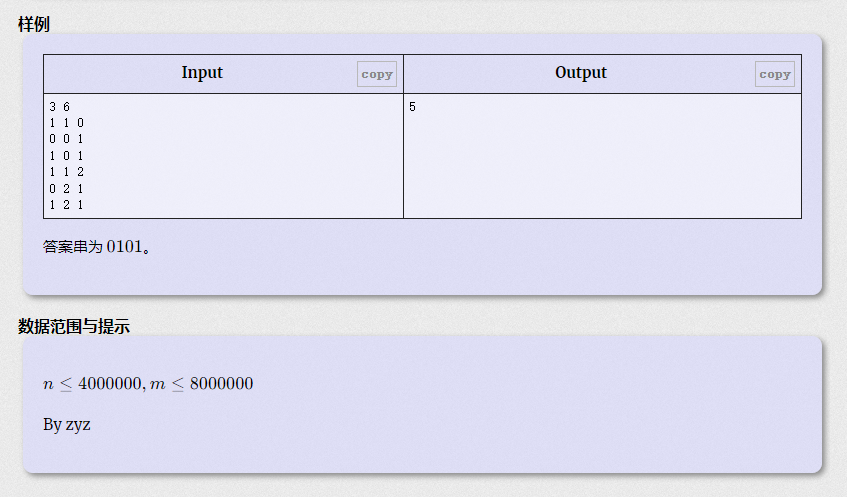
由于本题数据较大，因此输出的时候采用特殊的输出方式：用 00 或 11 代表每个询问的答案，将每个询问的答案依次从左到右排列，把得到的串视为一个二进制数，输出这个二进制数 \text{mod} ~ 998244353mod 998244353 的值。

请务必使用快读。

思想

并查集模板题，此题的特殊点在于二进制数的处理。

对于一个二进制数，在最右边加一个0就相当于 *2，加一个1相当于 *2+1。

代码

#include <iostream>
#include <vector>
#define SF                       \
    ios::sync_with_stdio(false); \
    cin.tie(0);                  \
    cout.tie(0);
using namespace std;
typedef long long ll;
const int inf = 0x7fffffff;
const ll p = 998244353;
int n, m;
vector<int> f;
inline int read() {
    int x = 0, f = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (ch >= '0' && ch <= '9') {
        x = (x << 1) + (x << 3) + (ch ^ 48);
        ch = getchar();
    }
    return x * f;
}
int getf(int u) {
    if (f[u] == u) return u;
    f[u] = getf(f[u]);
    return f[u];
}
void merge(int u, int v) {
    int t1, t2;
    t1 = getf(u), t2 = getf(v);
    if (t1 != t2) f[t2] = t1;
}
int main() {
    SF
        n = read(),
        m = read();
    f.resize(n + 10);
    for (int i = 0; i <= n; ++i) f[i] = i;
    ll ans = 0;
    while (m--) {
        int op, u, v;
        op = read(), u = read(), v = read();
        if (op == 0)
            merge(u, v);
        else {
            int t1, t2;
            t1 = getf(u), t2 = getf(v);
            if (t1 == t2) {
                ans = (ans * 2) % p;
                ans = (ans + 1) % p;
            } else
                ans = (ans * 2) % p;
        }
    }
    cout << ans << endl;
    return 0;
}

---

B - Learning Languages

题目

The "BerCorp" company has got n employees. These employees can use m approved official languages for the formal correspondence. The languages are numbered with integers from 1 to m. For each employee we have the list of languages, which he knows. This list could be empty, i. e. an employee may know no official languages. But the employees are willing to learn any number of official languages, as long as the company pays their lessons. A study course in one language for one employee costs 1 berdollar.

Find the minimum sum of money the company needs to spend so as any employee could correspond to any other one (their correspondence can be indirect, i. e. other employees can help out translating).

思想

其实就是要让所以员工都能联通。

将每种语言的掌握者分别用并查集合并，最后搜索一遍看看有多少个集合，集合的数量-1就是答案。

注意

1、要考虑特殊情况：所有员工一种语言都不会，那答案就是员工数量n。

代码

#include <iostream>
#include <vector>
#define SF                       \
    ios::sync_with_stdio(false); \
    cin.tie(0);                  \
    cout.tie(0);
using namespace std;
typedef long long ll;
const int inf = 0x7fffffff;
vector<int> a[150];
vector<int> f(150);
bool vis[150];
int cnt = 0;
int flag = 0;
int getf(int u) {
    if (f[u] == u) return u;
    f[u] = getf(f[u]);
    return f[u];
}
void merge(int u, int v) {
    int t1, t2;
    t1 = getf(u), t2 = getf(v);
    if (t1 != t2) {
        f[t2] = t1;
    }
}
int main() {
    SF int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) f[i] = i;
    for (int i = 1; i <= n; ++i) {
        int t;
        cin >> t;
        if (t != 0) flag = 1;
        for (int j = 1; j <= t; ++j) {
            int v;
            cin >> v;
            a[v].emplace_back(i);
        }
    }
    for (int i = 1; i <= m; ++i) {
        for (int j = 1; j < a[i].size(); ++j) {
            merge(a[i][j], a[i][j - 1]);
        }
    }
    for (int i = 1; i <= n; ++i) vis[getf(i)] = 1;
    for (int i = 1; i <= n; ++i)
        if (vis[i]) cnt++;
    if (flag == 1)
        cout << cnt - 1 << endl;
    else
        cout << n << endl;
    return 0;
}

---

D - Equals

题目

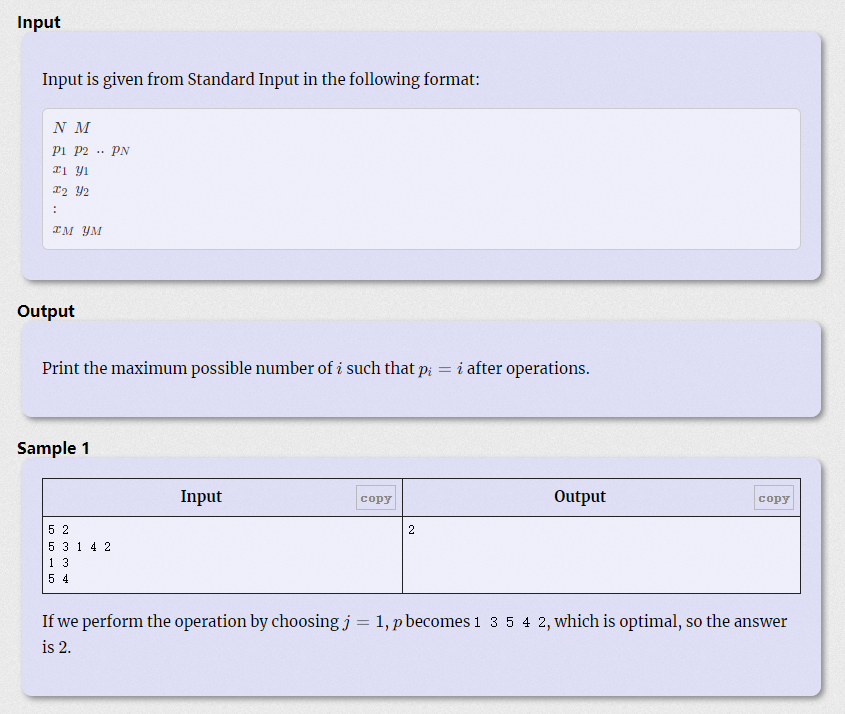
We have a permutation of the integers from 11 through NN, p_1p1, p_2p2, .., p_Np**N. We also have MM pairs of two integers between 11 and NN (inclusive), represented as (x_1,y_1)(x1,y1), (x_2,y_2)(x2,y2), .., (x_M,y_M)(x**M,y**M). AtCoDeer the deer is going to perform the following operation on pp as many times as desired so that the number of ii (11 ≤≤ ii ≤≤ NN) such that p_i = ip**i=i is maximized:

• Choose jj such that 11 ≤≤ jj ≤≤ MM, and swap p_{x_j}pxj and p_{y_j}pyj.

Find the maximum possible number of ii such that p_i = ip**i=i after operations.

思想

题目的意思是找出最终当前数字和下标能匹配上的数量的最大值。

所以就是将可调换位置的数字都用并查集合并到一个集合里，然后依次检查每个位置，如果当前位置的数字和此位置的下标在同一个集合里，说明调换位置后可以成功匹配，cnt++。

代码

#include <iostream>
#define SF                       \
    ios::sync_with_stdio(false); \
    cin.tie(0);                  \
    cout.tie(0);
using namespace std;
typedef long long ll;
const int inf = 0x7fffffff;
const int N = 1e5 + 10;
int a[N], f[N];
int getf(int u) {
    if (f[u] == u) return u;
    return f[u] = getf(f[u]);
}
void merge(int u, int v) {
    u = getf(u), v = getf(v);
    if (u != v) f[v] = u;
}
int main() {
    SF int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) f[i] = i;
    for (int i = 1; i <= n; ++i) cin >> a[i];
    for (int i = 1; i <= m; ++i) {
        int u, v;
        cin >> u >> v;
        merge(u, v);
    }
    ll cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (getf(a[i]) == getf(i)) cnt++;
    }
    cout << cnt << endl;
    return 0;
}

---

F - Built?

题目

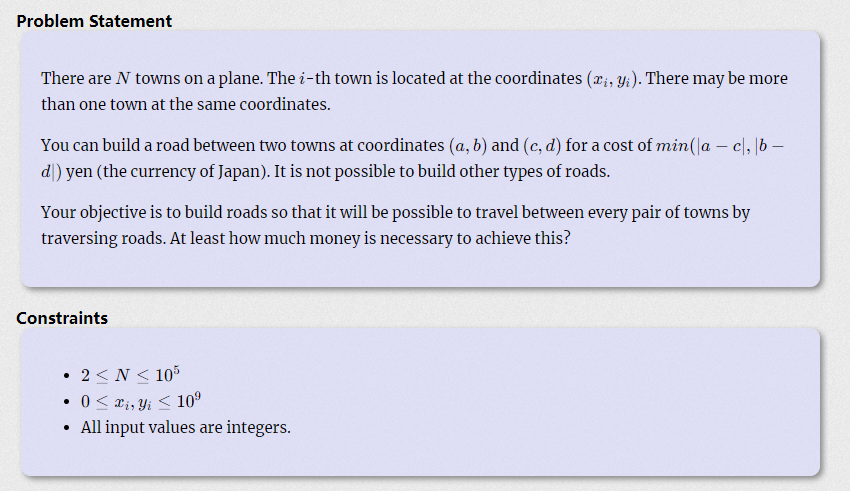
There are NN towns on a plane. The ii-th town is located at the coordinates (x_i,y_i)(x**i,y**i). There may be more than one town at the same coordinates.

You can build a road between two towns at coordinates (a,b)(a,b) and (c,d)(c,d) for a cost of min(|a-c|,|b-d|)min(∣a−c∣,∣b−d∣) yen (the currency of Japan). It is not possible to build other types of roads.

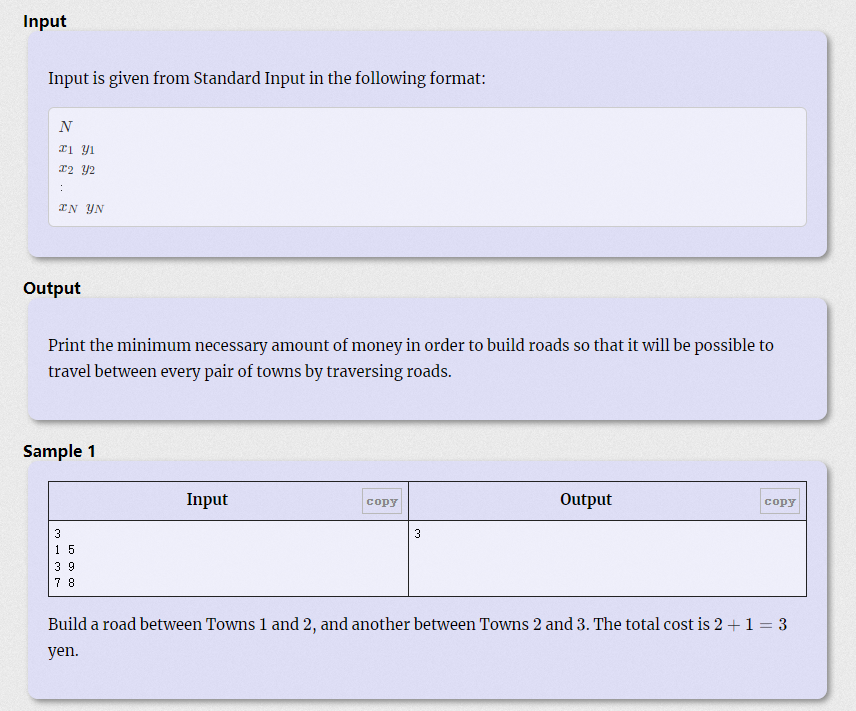
Your objective is to build roads so that it will be possible to travel between every pair of towns by traversing roads. At least how much money is necessary to achieve this?

思想

此题是用kruskal算法找最小生成树。

但由于数据范围较大，需要先优化一下数据。

由题目可知：

两个城市的距离是x轴或者y轴距离的最小值，所以我们可以分别对x轴、y轴排序，将坐标和距离压入新容器，再对新容器进行排序，对排序结果使用kruskal算法。

代码

#include <algorithm>
#include <iostream>
#include <queue>
#include <vector>
#define SF                       \
    ios::sync_with_stdio(false); \
    cin.tie(0);                  \
    cout.tie(0);
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x7fffffff;
const int N = 1e5 + 10;
struct node {
    int x, y, i;
} a[N];
struct node2 {
    int u, v, z;
};
vector<node2> b;
int f[N];
bool cmp(node aa, node bb) {
    return aa.x < bb.x;
}
bool cmp2(node aa, node bb) {
    return aa.y < bb.y;
}
bool cmp3(node2 aa, node2 bb) {
    return aa.z < bb.z;
}
ll getf(ll u) {
    if (f[u] == u) return u;
    return f[u] = getf(f[u]);
}
void merge(int u, int v) {
    u = getf(u), v = getf(v);
    if (u != v) f[v] = u;
}
int main() {
    SF int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) f[i] = i;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i].x >> a[i].y;
        a[i].i = i;
    }
    sort(a + 1, a + 1 + n, cmp);
    for (int i = 1; i < n; ++i) {
        node2 t;
        t.u = a[i].i, t.v = a[i + 1].i, t.z = a[i + 1].x - a[i].x;
        b.emplace_back(t);
    }
    sort(a + 1, a + 1 + n, cmp2);
    for (int i = 1; i < n; ++i) {
        node2 t;
        t.u = a[i].i, t.v = a[i + 1].i, t.z = a[i + 1].y - a[i].y;
        b.emplace_back(t);
    }
    sort(b.begin(), b.end(), cmp3);
    ll ans = 0, cnt = 0;
    for (int i = 0; i < b.size(); ++i) {
        int fu = getf(b[i].u), fv = getf(b[i].v);
        if (fu != fv) {
            merge(fu, fv);
            ans += b[i].z;
            cnt++;
        }
        if (cnt >= n - 1) break;
    }
    cout << ans << endl;
    return 0;
}