2022GDUT寒假专题学习-2
题单链接:专题训练2-DP - Virtual Judge (vjudge.net)
A - 拦截导弹
题目
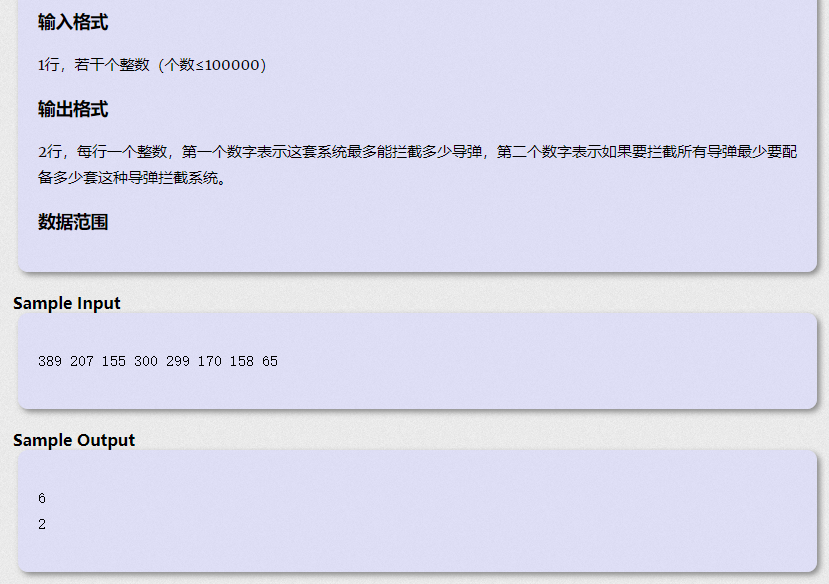
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。输入导弹依次飞来的高度(雷达给出的高度数据是不大于30000的正整数),计算这套系统最多能拦截多少导弹,如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。
思想
关于这道题我其实已经写过一篇随笔了:求最长子序列(非连续)的STL方法 - 洛谷P1020 [NOIP1999 普及组] 导弹拦截
用的是STL二分的方法O(nlogn),虽说此题在dp题单里,但用普通dp做的话,时间复杂度是O(n^2),就过不了了,但可以用树状数组优化,优化后的dp时间复杂度也为O(nlogn)。(明明还是STL二分的方法方便啊)
这里我就先不讲树状数组了,等有空了再补一篇(嘿嘿)
此题需求出最多能拦截多少导弹和要拦截所有导弹最少要配备系统的数量。
可以转换成求最长不上升子序列和最长上升子序列。
注意
1、lower_bound返回的是第一个大于等于x的数的位置,这里用于求最长上升子序列。
2、upper_bound返回的是第一个大于x的数的位置,这里用于求最长不上升子序列。
3、greater
代码
#include <algorithm>
#include <iostream>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int a[N], up[N], nup[N];
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n = 0;
while (cin >> a[++n])
;
n--;
int cnt1 = 1, cnt2 = 1;
nup[1] = up[1] = a[1];
for (int i = 2; i <= n; ++i) {
if (a[i] <= nup[cnt1])
nup[++cnt1] = a[i];
else {
int pos = upper_bound(nup + 1, nup + 1 + cnt1, a[i], greater<int>()) - nup;
nup[pos] = a[i];
}
if (a[i] > up[cnt2])
up[++cnt2] = a[i];
else {
int pos = lower_bound(up + 1, up + 1 + cnt2, a[i]) - up;
up[pos] = a[i];
}
}
cout << cnt1 << " " << cnt2 << endl;
return 0;
}
B - 最长公共子序列
题目
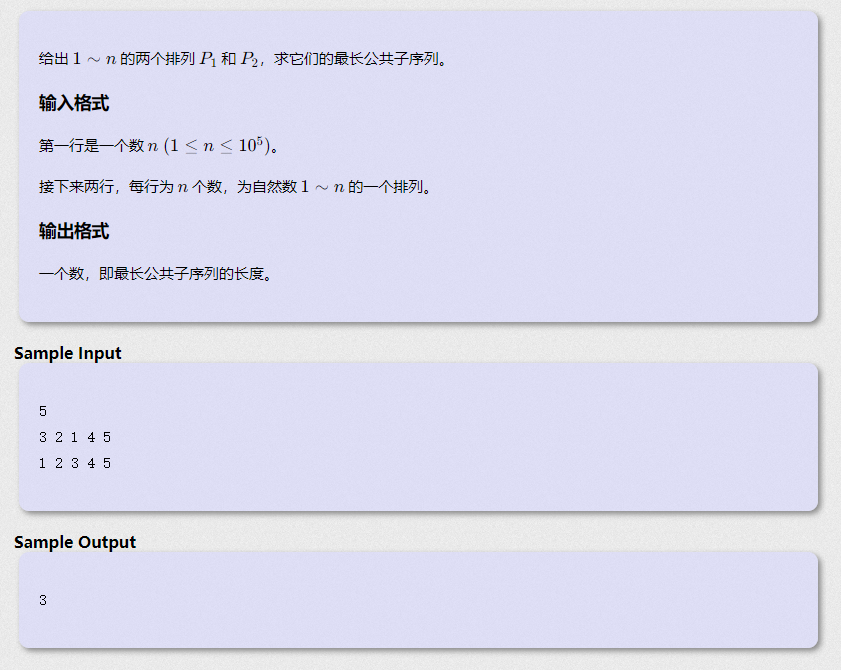
给出 1\sim n1∼n 的两个排列 P_1P1 和 P_2P2,求它们的最长公共子序列。
思想
关于LCS问题,可以通过离散化转换为LIS问题,于是就可以使用STL二分的方法O(nlogn)解决LCS问题!
先将a数组与一个递增的数列1,2,3...n两两对应(t数组),再把b数组中每个数在a数组中的位置表示成c数组,
经过此番操作,a与b的公共子序列在c数组中就是呈递增状态的。
代码
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int a[N], b[N], c[N], r[N], t[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n;
cin >> n;
for (int i = 1; i <= n; ++i)
{
cin >> a[i];
t[a[i]] = i;//a数组与递增数列1,2,3...n对应
}
for (int i = 1; i <= n; ++i)
cin >> b[i];
for (int i = 1; i <= n; ++i)
{
c[i] = t[b[i]];//将b数组中每个元素在a数组中的位置写入c数组
}
int cnt = 0;
for (int i = 1; i <= n; ++i)//使用求解LIS问题的STL二分方法
{
if (c[i] > r[cnt])
r[++cnt] = c[i];
else
{
int pos = lower_bound(r + 1, r + 1 + cnt, c[i]) - r;
r[pos] = c[i];
}
}
cout << cnt << endl;
return 0;
}
C - 开餐馆
题目
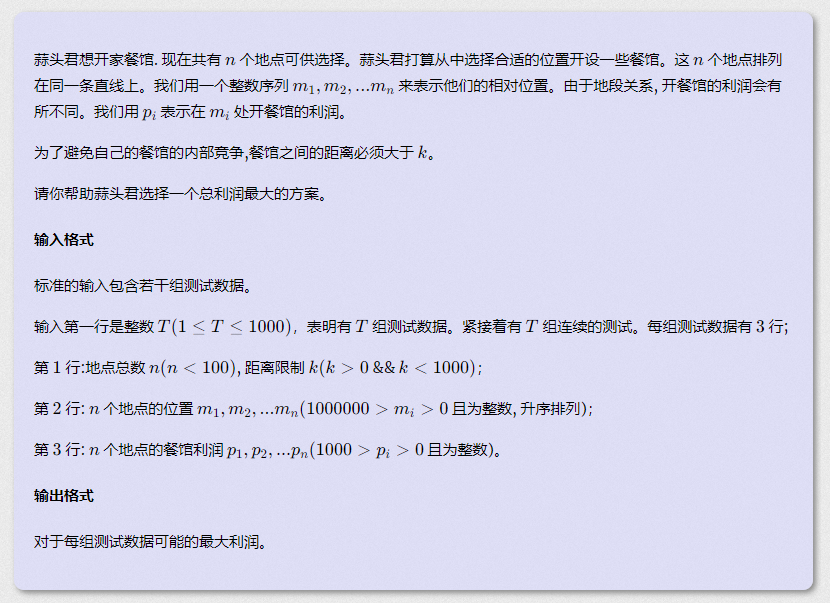
蒜头君想开家餐馆. 现在共有 nn 个地点可供选择。蒜头君打算从中选择合适的位置开设一些餐馆。这 nn 个地点排列在同一条直线上。我们用一个整数序列 m_1, m_2, ... m_nm1,m2,...m**n 来表示他们的相对位置。由于地段关系, 开餐馆的利润会有所不同。我们用 p_ip**i 表示在 m_im**i 处开餐馆的利润。
为了避免自己的餐馆的内部竞争,餐馆之间的距离必须大于 kk。
请你帮助蒜头君选择一个总利润最大的方案。

思想
遍历每一个地点,与在此之前的所有满足条件的餐馆取最大值。
代码
#include <algorithm>
#include <cstring>
#include <iostream>
#include <queue>
#include <vector>
#define SF ios::sync_with_stdio(false), cin.tie(0), cout.tie(0)
using namespace std;
typedef long long ll;
typedef pair<ll, ll> P;
const int inf = 0x3f3f3f3f;
int main() {
SF;
int T;
cin >> T;
while (T--) {
int n, k;
cin >> n >> k;
vector<int> m(n + 1), p(n + 1);
for (int i = 1; i <= n; ++i) cin >> m[i];
for (int i = 1; i <= n; ++i) cin >> p[i];
vector<int> dp(n + 1);
for (int i = 1; i <= n; ++i) {
dp[i] = p[i];
for (int j = 1; j < i; ++j) {
if (m[i] - m[j] > k) dp[i] = max(dp[i], dp[j] + p[i]);
}
}
int ma = -inf;
for (int i = 1; i <= n; ++i) {
ma = max(ma, dp[i]);
}
cout << ma << '\n';
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号