RSA算法是由MIT的Ron Rivest,Adi Shamir和Len Adleman于1977年提出并于1978年发表的算法。自其诞生之日起,该算法就成为被广泛接受并实现的通用公钥加密方法。
算法描述
RSA算法使用乘方模运算,明文以分组为单位进行加密,每个分组的二进制值均小于模n(为两个大素数的乘积),在实际应用中,分组的大小是i位,其中2i < n ≤ 2i+1
对明文分组M和密文分组C,加密和解密过程如下:
C = Me mod n
M = Cd mod n = Med mod n
公钥为PU = {e , n} 私钥位PR = {d , n}
该算法用到下列元素:
两个素数p,q (保密的,选定的)
n = pq (公开的,计算得出的)
e满足gcd(φ(n) , e) = 1; 1 < e < φ(n) (公开的,选定的)
d ≡ e-1 (mod φ(n)) (保密的,计算得出的)
当e和d互为模φ(n)的乘法逆时,Med mod n = M (当e与φ(n)互素时必有乘法逆)
证明: ed mod φ(n) = 1 等效于 ed = kφ(n) + 1 k∈Z
Mkφ(n) + 1 mod n = Mk(p - 1)(q - 1) + 1 mod n n = p × q
首先可证明 Mk(p - 1)(q - 1 ) + 1 mod p = M mod p
若M与p不互素,由于p是素数,则p必可整除M,此时M mod p = 0
Mk(p - 1)(q - 1) + 1 mod p = 0 = M mod p
若M与p互素,由欧拉定理,Mφ(p) mod p = 1
Mk(p - 1)(q - 1) + 1 mod p = [(M)Mk(p - 1)(q - 1) ] mod p
= [(M)(M(p - 1))k(q - 1) ] mod p
= [(M)(Mφ(p))k(q - 1) ] mod p
= (M mod p) × [(Mφ(p)) mod p]k(q - 1)
= M mod p
[Mk(p - 1)(q - 1) + 1 - M] mod p = [Mk(p - 1)(q - 1) + 1 mod p] - [M mod p] = 0
因此p整除[Mk(p - 1)(q - 1) + 1 - M] ,同理q也整除[Mk(p - 1)(q - 1) + 1 - M]。因为p和q是不同的素数,所以必定存在一个整数r满足:
[Mk(p - 1)(q - 1) + 1 - M] = px1 = qx2 = pqr = nr
故n整除[Mk(p - 1)(q - 1) + 1 - M],所以Mkφ(n) + 1 mod n = Mk(p - 1)(q - 1) + 1 mod n = M
RSA的加密、解密过程及实例
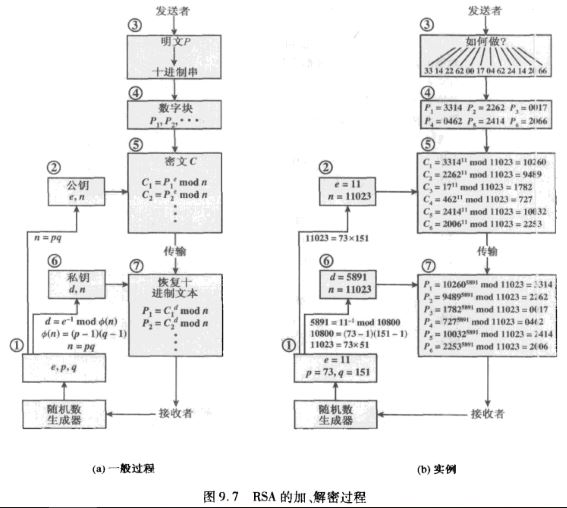
在这个例子中,明文是一串字母,每个字母与一个两位的十进制数字对应(如a=00,A=26),明文的每一分组块由四个十进制数字组成,即两个字母。
计算上的简化
1、模算术里的求幂运算
通过两个技巧进行计算上的简化,
1.应用模算术的以下性质来计算模幂运算,以避免先求幂再求模带来中间值过大的问题
[(a mod n) × (b mod n)] mod n = (a × b) mod n
2.因为RSA中所用指数很大,所以还应考虑幂运算的效率问题。如x16,若直接计算需要15次乘法,如果重复计算每个中间结果的平方,得到x2,x4,x8,x16,那么只需要4次乘法。同理,计算x11 mod n,可以先计算 x mod n,x2 mod n,x4 mod n,x8 mod n,再计算[(x mod n) × (x2 mod n) × (x8 mod n)] mod n
更一般地,假定我们要计算ab,其中a,b∈正整数。若将b表示成二进制数bkbk-1···b0,则更加方便提高幂运算的效率。
2、用公钥进行有效运算
为了加快RSA算法在使用公钥是的运算速度,通常会选择一个特定的e,大多数情况下选为65537(216+1),其它两个常用的选择是3和17。之所以选这些数,是因为这些数里都只有两个有效位(65537 = 1000 0000 0000 0001b, 3 = 11, 17 = 1 0001),所以在求幂运算时需要的乘法次数极小化了。
如果指数太小,如e = 3,RSA甚至会遭受一些简单的攻击,假设有三个不同的RSA用户,他们都使用指数e = 3,但是他们的模数n各不相同,即n1,n2,n3。现有一用户A以加密方式给他们三个发送相同的消息M,则三个密文为:C1 = M3 mod n1,C2 = M3 mod n2,C3 = M3 mod n3。很有可能n1,n2,n3是两两互素的,所以运用中国剩余定理可以计算出M3 mod (n1n2n3)。根据RSA规则,M应该比模数ni小,所以有M3 < n1n2n3,从而攻击者只要计算M3就可以了。解决办法是给每一个待加密的消息分组M填充一个唯一的伪随机位串可以阻止这种攻击。
此外,由于选定了e,为了确保e和φ(n)互素,因为e = 65537 是素数,p,q是大素数,故所选p,q需要满足以下式子
[(p-1)×(q-1)] mod e ≠ 0
[(p-1) mod e × (q-1) mod e] mod e ≠ 0
(p-1) mod e ≠ 0 且 (q-1) mod e ≠ 0
3、用私钥进行有效运算
由于d不像e一样是选定的为简化计算的值,为了加快幂运算,可以运用中国剩余定理。先定义一些中间值:
Vp = Cd mod p Vq = Cd mod q
应用CRT的公式有:
Xp = q × (q-1 mod p) Xq = p × (p-1 mod q)
M = (VpXp + VqXq) mod n
进一步用费马定理简化Vp,Vq的计算,即如果p和a互素,则ap-1 ≡ 1 (mod p),则
Vp = Cd mod p = Ck(p-1)+d mod (p-1) mod p = Ck(p-1) mod p × Cd mod (p-1) mod p
= Cd mod (p-1) mod p
同理 Vq = Cd mod q = Cd mod (q-1) mod q
其中d mod (p-1),d mod (q-1),Xp,Xq(求乘法逆元素可用扩展Euclid算法计算)都可预先计算出来,和直接计算M = Cd mod n相比,上述的计算速度大约快4倍。
4、密钥产生
在应用公钥密码进行通信之前,通信各方都必须产生一对密钥,即
1.确定两个素数p和q
2.选择e,并计算d
首先为避免穷举攻击,p和q必须是大素数,此外要选择有效的算法来产生这样的大素数。目前并没有有效的方法产生任意大素数,因此通常的方法是随机挑选一个期望大小的奇数,然后测试它是否是素数,若不是则挑选下一个随机数直至检测到素数为止。这里用到的各种素性测试方法几乎都是概率测试方法,需要执行多次才能尽可能逼近100%。
由数论中的素数定理可知,在N附近平均每隔lnN个整数就有一个素数,这样在找到一个素数之前,平均要测试大约lnN个整数。由于每隔偶数会被立即拒绝,故实际只需要测试lnN/2个整数。
若先确定e,则需要进一步筛选满足(p-1) mod e ≠ 0 (q-1) mod e ≠ 0 的p和q。
若后确定e,则需选择满足gcd(φ(n) , e) = 1 的e
最后应用扩展Euclid算法计算 d ≡ e-1 (mod φ(n))
RSA的安全性
对RSA算法的攻击可能有如下4种方式:
穷举攻击:试图穷举所有可能的密钥
数学攻击:实质是试图分解两个素数的乘积
计时攻击:依赖于解密算法的运行时间
选择密文攻击:利用了RSA算法的性质
数学攻击
用数学攻击RSA的途径有以下三种:
1、分解n为两个素因子,从而计算出φ(n) = (p-1)(q-1),进而确定d ≡ e-1 (mod φ(n))
2、直接确定φ(n)而不去确定p和q,这样也能计算出d ≡ e-1 (mod φ(n))
3、直接确定d,而不确定φ(n)
对RSA的密码分析的讨论大都集中在第一种攻击方式,即因子分解n。现在已知从e和n确定d的算法至少和因子分解n一样费时,因此,我们可以将因子分解的性能作为基准来评价RSA的安全性。随着计算能力的不断增强,目前密钥大小取1024到2048位是合适的。此外p和q最好还满足以下限制条件:
1、p和q的长度应仅相差几位,对1024位(309个十进制位)的密钥而言,p和q都应约在1075到10100之间。
2、(p-1)和(q-1)都应有一个大的素因子。
3、gcd(p-1,q-1)应该较小
另外已证明,若e<n且d<n1/4,则d很容易被确定
计时攻击
攻击者可以通过记录计算机解密消息所用的时间来确定私钥。由于模乘函数的执行时间只在几种情形中其执行时间比整个模幂运算的平均执行时间要长得多,但在大多数情形下其执行速度相当快,计时攻击从最左位bk开始,一位一位地执行,攻击者根据每次执行时间的长度来推算。
解决办法:
1、不变的幂运算时间:保证所有幂运算在返回结果前执行的时间都相同。这种方法虽然简单,但会降低算法的性能。
2、随机延时:通过在求幂算法中加入随机延时来迷惑攻击者
3、隐蔽:执行幂运算之前先将密文乘上一个随机数,使得攻击者不知道计算机正在处理的是密文的哪些位,以防止攻击者一位一位地进行分析吗,而这种分析正是计时攻击的本质所在。
RSA数据安全公司在它们产品中就使用了隐蔽方法,其具体实现如下
1、产生0只n-1之间的秘密的随机数r
2、计算C’ = Cre mod n
3、计算M’ = (C’)d mod n
4、计算M = M’r-1 mod n 其中r-1是r的模n的乘法逆元。根据red mod n = r mod n可证明结论是正确的,据RSA公司声称应用了该隐蔽方法,运算性能降低了2%-10%
选择密文攻击
基本的RSA算法易受选择密文攻击(CCA)。攻击者可以选择一个明文,运用目标对象的公钥加密,然后再通过某些手段获得目标对象用私钥对密文解密后的明文。看起来好像没什么用处,实则不然,攻击者实际上是将需破解的密文做了一番数学包装后,再发给攻击目标,由于解密后的明文咋看起来不是重要机密,因此就较容易被截获或者盗取。
利用CCA攻击RSA利用了RSA如下的性质
E(PU , M1) × E(PU , M2) = E(PU , [M1 × M2])
进而用如下方式解密C = Me mod n
1、计算 X = (C × 2e) mod n = (Me mod n) × (2e mod n) = (2M)e mod n
2、将X作为选择明文提交,并收到Y = Xd mod n = (2M)ed mod n = 2M
为了防止这种简单攻击,实用的基于RSA的密码体制在加密之前都会对明文进行随机填充。不过简单的随机填充已被证明不足以提高期望的安全性,因此RSA公司推荐了一种称为最优非对称加密填充(OAEP)的程序对明文进行修改。

1、首先将加密参数P通过Hash函数处理并输出到整体数据块DB一侧,明文的值也整体复制到DB的另一侧,DB剩余部分用0进行填充。
2、然后随机选择一个种子,使用一种叫做掩码生成函数MGF,输出的Hash值和DB异或产生maskedDB。
3、该maskedDB同样通过MGF函数,输出Hash值与种子进行异或产生MaskedSeed
4、最后MaskedSeed和maskedDB共同组成EM作为最终的填充结果。
加密公式 DB = H(P) || Padding || M
maskedDB = DB⊕MGF(Seed)
maskedSeed = Seed⊕MGF(maskedDB)
EM = maskedSeed || maskedDB
解密公式 Seed = maskedSeed⊕MGF(maskedDB)
DB = maskedDB⊕MGF(Seed)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号