【算法】滑动窗口三步走
滑动窗口介绍
对于大部分滑动窗口类型的题目,一般是考察字符串的匹配。比较标准的题目,会给出一个模式串B,以及一个目标串A。然后提出问题,找到A中符合对B一些限定规则的子串或者对A一些限定规则的结果,最终再将搜索出的子串完成题意中要求的组合或者其他。
比如:给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。
又或者:给你一个字符串 S、一个字符串 T,请在字符串 S 里面找出:包含 T 所有字母的最小子串。
再如:给定一个字符串 s 和一些长度相同的单词 words。找出 s 中恰好可以由 words 中所有单词串联形成的子串的起始位置。
都是属于这一类的标准题型。而对于这一类题目,我们常用的解题思路,是去维护一个可变长度的滑动窗口。无论是使用双指针,还是使用双端队列,又或者用游标等其他奇技淫巧,目的都是一样的。滑动窗口的原理都是一致的,只不过改变了实现方法而已。
简介
学过计算机网络的同学,都知道滑动窗口协议(Sliding Window Protocol),该协议是 TCP协议 的一种应用,用于网络数据传输时的流量控制,以避免拥塞的发生。该协议允许发送方在停止并等待确认前发送多个数据分组。由于发送方不必每发一个分组就停下来等待确认。因此该协议可以加速数据的传输,提高网络吞吐量。
滑动窗口算法其实和这个是一样的,只是用的地方场景不一样,可以根据需要调整窗口的大小,有时也可以是固定窗口大小。
滑动窗口算法(Sliding Window Algorithm)
Sliding window algorithm is used to perform required operation on specific window size of given large buffer or array.
滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作。
This technique shows how a nested for loop in few problems can be converted to single for loop and hence reducing the time complexity.
该技术可以将一部分问题中的嵌套循环转变为一个单循环,因此它可以减少时间复杂度。
简而言之,滑动窗口算法在一个特定大小的字符串或数组上进行操作,而不在整个字符串和数组上操作,这样就降低了问题的复杂度,从而也达到降低了循环的嵌套深度。其实这里就可以看出来滑动窗口主要应用在数组和字符串上。
基本示例
如下图所示,设定滑动窗口(window)大小为 3,当滑动窗口每次划过数组时,计算当前滑动窗口中元素的和,得到结果 res。
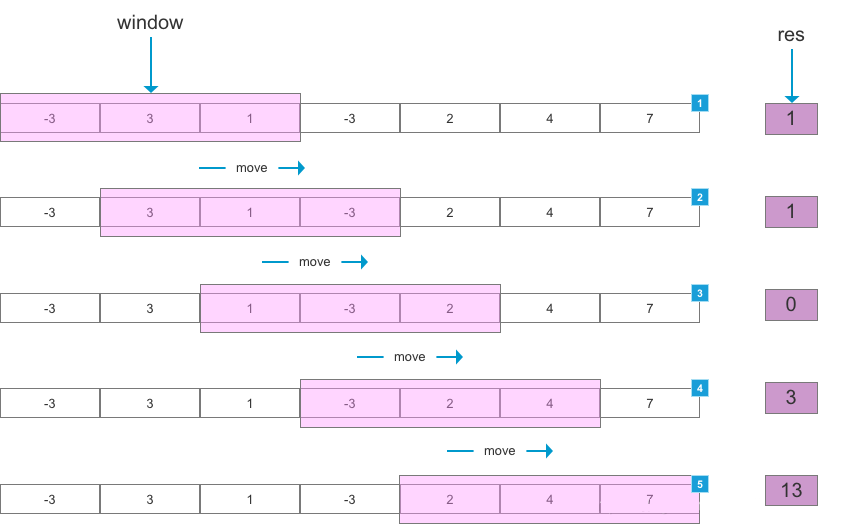
可以用来解决一些查找满足一定条件的连续区间的性质(长度等)的问题。由于区间连续,因此当区间发生变化时,可以通过旧有的计算结果对搜索空间进行剪枝,这样便减少了重复计算,降低了时间复杂度。往往类似于“ 请找到满足 xx 的最 x 的区间(子串、子数组)的 xx ”这类问题都可以使用该方法进行解决。
需要注意的是,滑动窗口算法更多的是一种思想,而非某种数据结构的使用。
什么是滑动窗口
滑动窗口可以看成数组中框起来的一个部分。在一些数组类题目中,我们可以用滑动窗口来观察可能的候选结果。当滑动窗口从数组的左边滑到了右边,我们就可以从所有的候选结果中找到最优的结果。
对于这道题来说,数组就是正整数序列 \([1, 2, 3, \dots, n]\)。我们设滑动窗口的左边界为 i,右边界为 j,则滑动窗口框起来的是一个左闭右开区间 \([i, j)\)。注意,为了编程的方便,滑动窗口一般表示成一个左闭右开区间。在一开始,\(i=1, j=1\),滑动窗口位于序列的最左侧,窗口大小为零。
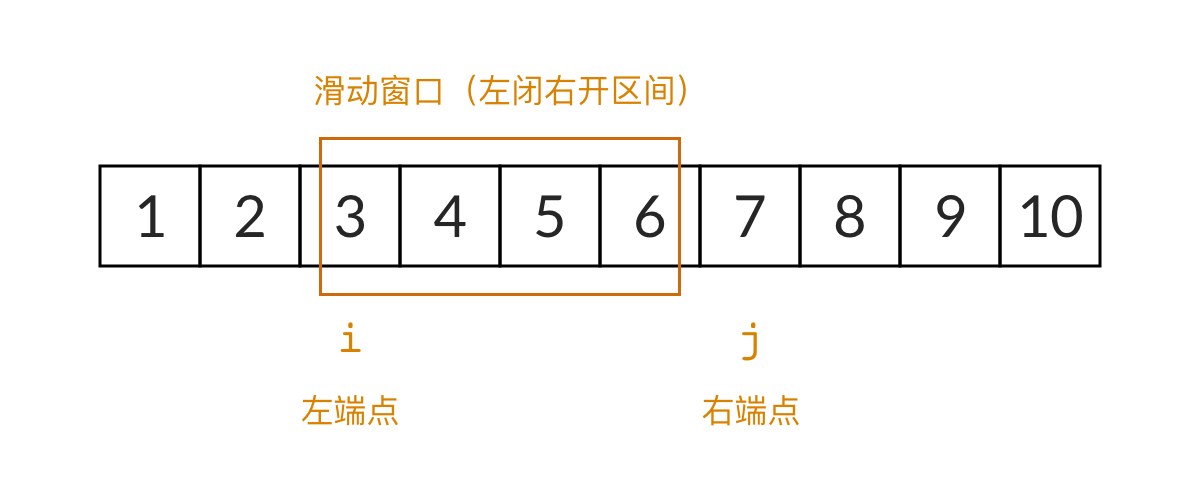
滑动窗口的重要性质是:窗口的左边界和右边界永远只能向右移动,而不能向左移动。这是为了保证滑动窗口的时间复杂度是 \(O(n)\)。如果左右边界向左移动的话,这叫做“回溯”,算法的时间复杂度就可能不止 \(O(n)\)。
在这道题中,我们关注的是滑动窗口中所有数的和。当滑动窗口的右边界向右移动时,也就是 j = j + 1,窗口中多了一个数字 j,窗口的和也就要加上 j。当滑动窗口的左边界向右移动时,也就是 i = i + 1,窗口中少了一个数字 i,窗口的和也就要减去 i。滑动窗口只有 右边界向右移动(扩大窗口) 和 左边界向右移动(缩小窗口) 两个操作,所以实际上非常简单。
如何用滑动窗口解这道题
要用滑动窗口解这道题,我们要回答两个问题:
- 第一个问题,窗口何时扩大,何时缩小?
- 第二个问题,滑动窗口能找到全部的解吗?
对于第一个问题,回答非常简单:
- 当窗口的和小于 target 的时候,窗口的和需要增加,所以要扩大窗口,窗口的右边界向右移动
- 当窗口的和大于 target 的时候,窗口的和需要减少,所以要缩小窗口,窗口的左边界向右移动
- 当窗口的和恰好等于 target 的时候,我们需要记录此时的结果。设此时的窗口为 \([i, j)\),那么我们已经找到了一个 i 开头的序列,也是唯一一个 i 开头的序列,接下来需要找 i+1 开头的序列,所以窗口的左边界要向右移动
对于第二个问题,我们可以稍微简单地证明一下:
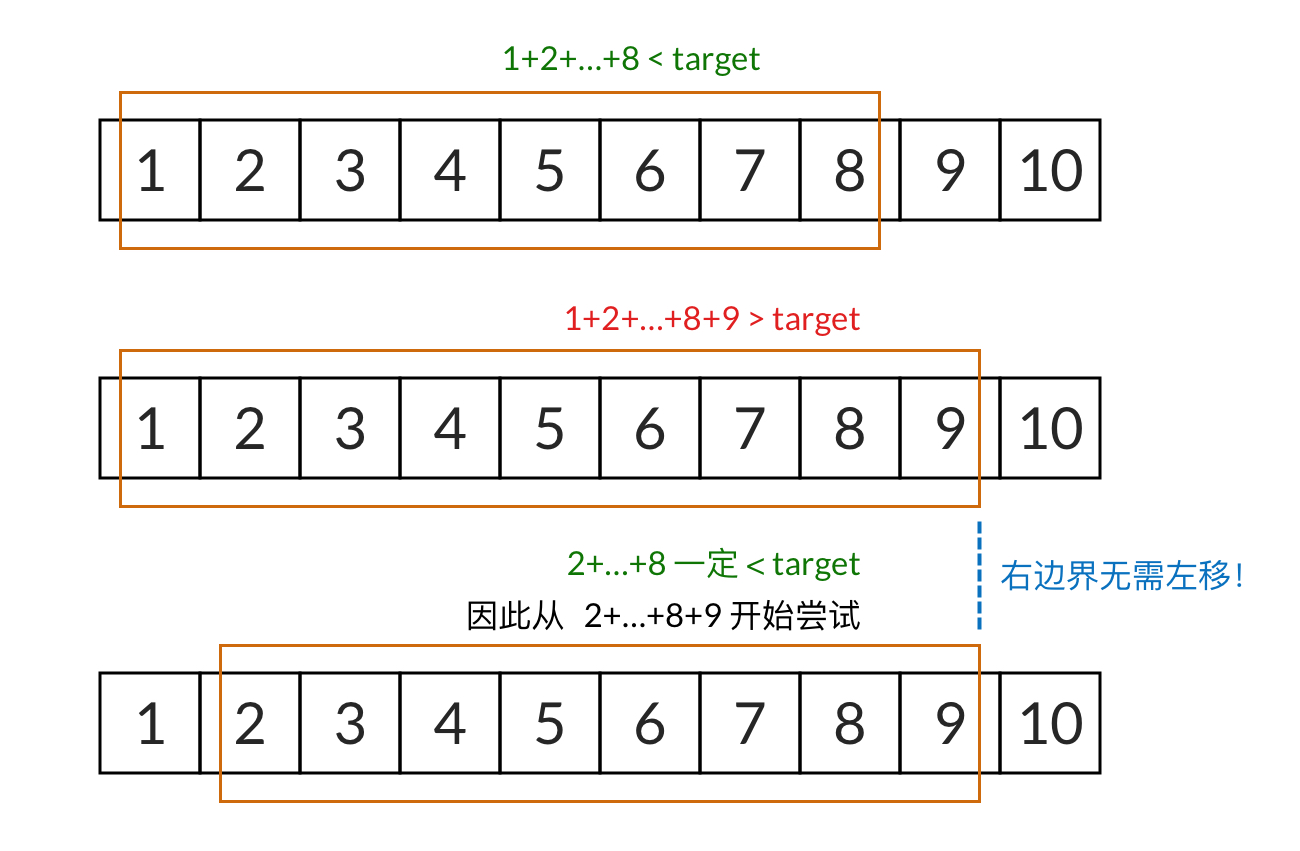
我们一开始要找的是 1 开头的序列,只要窗口的和小于 target,窗口的右边界会一直向右移动。假设 \(1+2+\dots+8\) 小于 target,再加上一个 9 之后, 发现 \(1+2+\dots+8+9\) 又大于 target 了。这说明 1 开头的序列找不到解。此时滑动窗口的最右元素是 9。
接下来,我们需要找 2 开头的序列,我们发现,\(2 + \dots + 8 < 1 + 2 + \dots + 8 < \mathrm{target}\)。这说明 2 开头的序列至少要加到 9。那么,我们只需要把原先 1~9 的滑动窗口的左边界向右移动,变成 2~9 的滑动窗口,然后继续寻找。而右边界完全不需要向左移动。
以此类推,滑动窗口的左右边界都不需要向左移动,所以这道题用滑动窗口一定可以得到所有的解。时间复杂度是 \(O(n)\)。
注:这道题当前可以用等差数列的求和公式来计算滑动窗口的和。不过我这里没有使用求和公式,是为了展示更通用的解题思路。实际上,把题目中的正整数序列换成任意的递增整数序列,这个方法都可以解。
适用场景
适用于需要以某一连续窗口范围的元素遍历数组,而不是单个遍历每个元素。
适用场景:
- 连续(可以通过排序使数组连续)
- 窗口大小
滑动窗口的适用条件(充分条件):滑动窗口一定要有限制
- 限制窗口内元素:窗口内元素有明确的目的性,比如 窗口内元素和为target,窗口内元素不重复等;
- 限制窗口大小:窗口大小固定,比如 窗口大小为k。
两者满足其一,即可使用滑动窗口法。
也就是说,窗口要满足某一个确定的条件,要么窗口大小确定,要么窗口内元素确定。
关键词:窗口、连续、范围
它可以解决如下问题:
- 最小覆盖子串(LeetCode76)
- 字符串排列(LeetCode567)
- 统计字母异位词(LeetCode438)
- 最长无重复子串(LeetCode3)
那么我们下面来看两题:
面试题 16.17. 连续数列
给定一个整数数组,找出总和最大的连续数列,并返回总和。
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
这两题怎么用滑动窗口来做?
各位发现了吗?根本找不到扩缩条件!
所以,我们的滑动窗口一定要有限制。
这两题我们窗口内元素都没有明确的目的性,我们不知道最大值是多少,不知道什么时候该扩缩,所以我们得考虑其他方法,这里可以看到是最优解问题,我们可以划分为多个滑动窗口阶段,可以考虑用动态规划来做。
暴力破解
固定一个边界(左边界或右边界),向前或向后连续遍历(窗口大小),遇到这种情况就可以使用滑动窗口来解决。
即 遍历每个元素,从每个元素开始遍历每个窗口。
滑动窗口数据
使用滑动窗口算法能够获取到的数据:
- 窗口大小
- 窗口内元素集合值(之和、乘积等)
技巧:做题之前如果发现数据杂乱无章,思考是否可以通过排序来使得数据可以利用。
滑动窗口三步走
设滑动窗口的左边界为 left,右边界为 right,则滑动窗口框起来的是一个左闭右开区间 \(\[left, right)\)。
滑动窗口前闭后开,也没想象的那么复杂,其实就是一个队列啦!我们写滑动窗口,其实就是手动实现一个队列啦!!!
详情请看:【数据结构】栈与队列
注意,为了编程的方便,滑动窗口一般表示成一个左闭右开区间。在一开始,\(left = 0, right = 0\),滑动窗口位于序列的最左侧,窗口大小为零。
滑动窗口只有 右边界向右移动(扩大窗口) 和 左边界向右移动(缩小窗口) 两个操作,所以实际上非常简单。
滑动窗口的适用条件:
- 限制窗口内元素:窗口内元素有明确的目的性,比如 窗口内元素和为target,窗口内元素不重复等;
- 限制窗口大小:窗口大小固定,比如 窗口大小为k。
两者满足其一,即可使用滑动窗口法。
也就是说,窗口要满足某一个确定的条件,要么窗口大小确定,要么窗口内元素确定。
窗口条件:(满足其一即可)
- 窗口大小确定
- 窗口内元素确定
特征:
- 前闭后开,left 元素包含在滑动窗口内,right 元素不包含在滑动窗口内
- 使用 right 来进行遍历元素,满足条件就
right++,加入滑动窗口 - 滑动窗口 left、right 只能前进,不能后退,所以一般循环范围只用比较最大值right是否超出边界即可
初始化:
- 固定窗口大小:
left = 0, right = 窗口大小,(窗口大小固定)注意:初始化固定窗口大小的时候,需要在最开始遍历从left到right的窗口内元素(
for (int i = left; i < right; i++)),然后再开始让窗口遍历前进while (right < nums.length)。 - 动态窗口大小:
left = 0, right = 0,(窗口内元素有明确的目的性,窗口内元素确定)
操作:
- 判断窗口大小:(前闭后开)
right - left或者(前闭后闭)right - left + 1 - 右边界向右移动(扩大窗口、入队):(双指针)
right++;或者 (双端队列)linkedList.addFirst(right); - 左边界向右移动(缩小窗口、出队):(双指针)
left++;或者 (双端队列)linkedList.removeLast();
注意:
滑动窗口一般用于判断字符串与子字符串,所以它常常与哈希表混合使用,使用两个哈希表,第一个来记录窗口中的元素出现次数,第二个来记录目标子字符串中的元素出现次数,然后两个哈希表元素出现次数进行比较。
滑动窗口可以看作一种队列,使用滑动窗口算法能够获取到的数据:
- 窗口大小
- 窗口内元素集合值(之和、乘积等)
sum = 0; // 队列内集合值
while (right < nums.length) {
if (满足条件) {
right++; // 入队
} else {
// 当不满足条件时先让左边界走,过滤掉不满足条件的元素
// left可能大于right,right <= left时,窗口都为空
left++; // 出队
}
}
滑动窗口三步走:
1. 明确限制条件
1.明确限制条件:
- 限制窗口内元素:窗口内元素有明确的目的性,比如 窗口内元素和为target,窗口内元素不重复等;
- 限制窗口大小:窗口大小固定,比如 窗口大小为k。
这两种限制条件分别对应了不同的循环条件
- 限制窗口内元素:
right < s.length(),由于只是限制了窗口内的元素,所以需要right右指针去进行探索遍历,符合条件才能加入窗口中。主角是right右指针,用右指针遍历整个数组,关注它是否满足条件即可。
- 限制窗口大小:
right <= s.length(),此时的right右指针只是充当窗口的前闭后开边界,而不是用于探索遍历了。主角是整个窗口,窗口内所有的元素,用整个窗口取遍历整个数组(所以right需要等于s.length(),因为right是开区间),关注它们组合是否满足条件。
明确循环条件:right 如何遍历数组?什么时候保持循环,什么时候结束循环?
注意:由于滑动窗口是利用队列的原理实现的,前闭后开,所以你得思考一下循环的条件是
right < s.length()还是right <= s.length()?
- 限制窗口内元素:有时候使用 right 来一个一个遍历访问元素时,我们
right < s.length()即可遍历完所有元素,如果right = s.length()那就数组元素越界了;- 限制窗口大小:如果我们有时候不使用 right 来一个一个遍历访问元素的话,即 right 只充当边界使用(前闭后开),那我们就需要
right <= s.length()才能通过窗口拿到窗口内所有元素
这里需要特别注意了!!!切勿生搬硬套!
2. 寻找扩缩条件
2.寻找扩缩条件:窗口何时扩大,何时缩小?
注意:这个扩大与缩小的时机得根据题意来具体情况具体分析,并没有一个详细的标准。
有时候题目限制滑动窗口的大小,所以我们得时刻关注窗口大小,并对窗口大小进行控制,小了增大,大了减小。
一般思路:rightIndex不断前进进行扩容,当窗口内元素不满足条件后,leftIndex不断收缩使当前窗口内元素满足条件。
int slidingWindow() {
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
while(right < s.size()) {
window.add(s[right]);
right++;
// 如果符合要求,说明窗口构造完成,移动 left 缩小窗口
while (window 符合要求) {
// 如果这个窗口的子串更短,则更新 res
res = minLen(res, window);
window.remove(s[left]);
left++;
}
}
return res;
}
3. 完成目标功能
3.完成目标功能:当滑动窗口满足条件时,完成目标功能。
注意:这个条件也有可能是对窗口大小的限制等。
滑动窗口法的大体框架
其实,滑动窗口就是通过不断调整子序列的 left 和 right 位置,从而获取满足要求的解。
在介绍滑动窗口的框架时候,大家先从字面理解下:
-
滑动:说明这个窗口是移动的,也就是移动是按照一定方向来的。
-
窗口:窗口大小并不是固定的,可以不断扩容直到满足一定的条件;也可以不断缩小,直到找到一个满足条件的最小窗口;当然也可以是固定大小。
为了便于理解,这里采用的是字符串来讲解。但是对于数组其实也是一样的。滑动窗口算法的思路是这样:
-
我们在字符串 S 中使用双指针中的左右指针技巧,初始化 left = right = 0,把索引闭区间 [left, right] 称为一个「窗口」。
-
我们先不断地增加 right 指针扩大窗口 [left, right],直到窗口中的字符串符合要求(包含了 T 中的所有字符)。
-
此时,我们停止增加 right,转而不断增加 left 指针缩小窗口 [left, right],直到窗口中的字符串不再符合要求(不包含 T 中的所有字符了)。同时,每次增加 left,我们都要更新一轮结果。
-
重复第 2 和第 3 步,直到 right 到达字符串 S 的尽头。
这个思路其实也不难,第 2 步相当于在寻找一个「可行解」,然后第 3 步在优化这个「可行解」,最终找到最优解。左右指针轮流前进,窗口大小增增减减,窗口不断向右滑动。
下面画图理解一下,needs 和 window 相当于计数器,分别记录 T 中字符出现次数和窗口中的相应字符的出现次数。
初始状态:
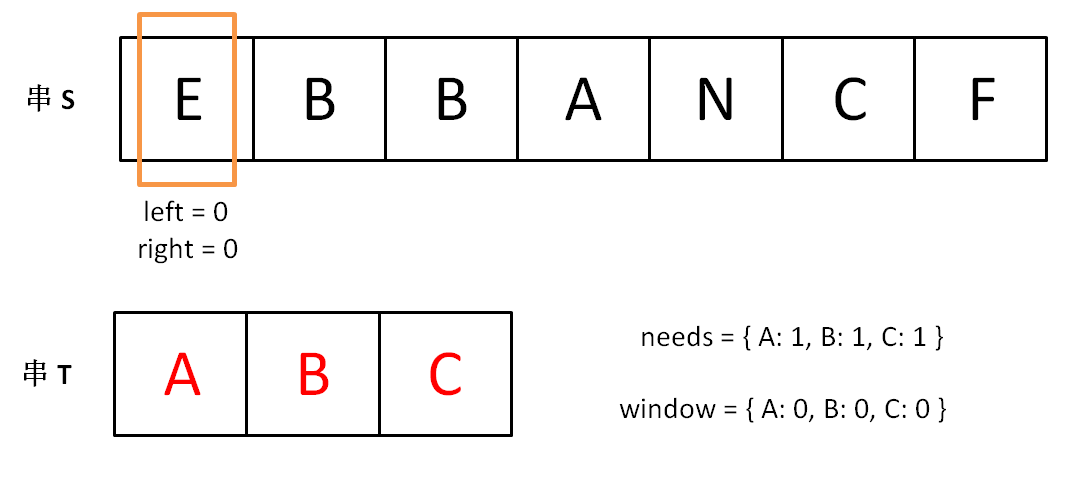
增加 right,直到窗口 [left, right] 包含了 T 中所有字符:

现在开始增加 left,缩小窗口 [left, right]。
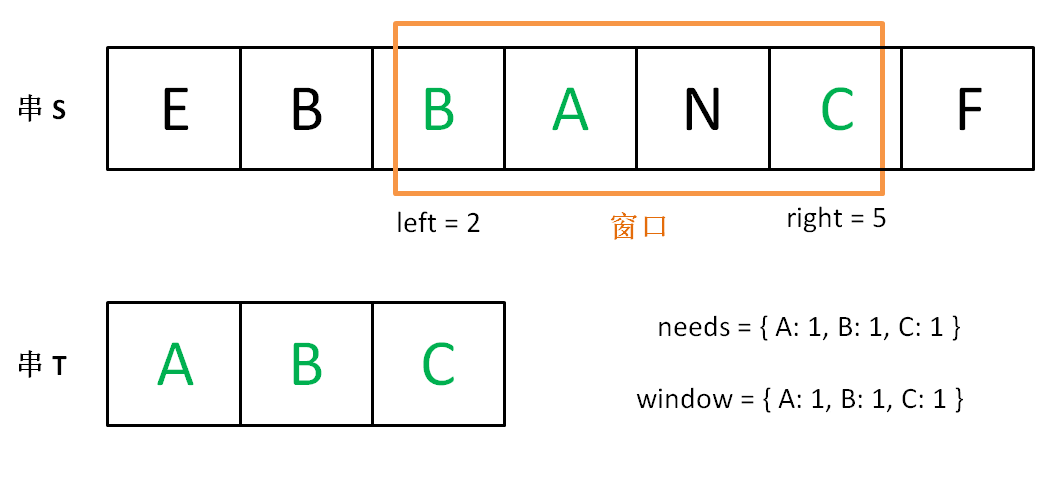
直到窗口中的字符串不再符合要求,left 不再继续移动。

之后重复上述过程,先移动 right,再移动 left…… 直到 right 指针到达字符串 S 的末端,算法结束。
如果你能够理解上述过程,恭喜,你已经完全掌握了滑动窗口算法思想。至于如何具体到问题,如何得出此题的答案,都是编程问题,等会提供一套模板,理解一下就会了。
上述过程对于非固定大小的滑动窗口,可以简单地写出如下伪码框架:
int slidingWindow() {
string s, t;
// 在 s 中寻找 t 的「最小覆盖子串」
int left = 0, right = 0;
string res = s;
while(right < s.size()) {
window.add(s[right]);
right++;
// 如果符合要求,说明窗口构造完成,移动 left 缩小窗口
while (window 符合要求) {
// 如果这个窗口的子串更短,则更新 res
res = minLen(res, window);
window.remove(s[left]);
left++;
}
}
return res;
}
但是,对于固定窗口大小,可以总结如下:
int slidingWindow() {
// 固定窗口大小为 k
string s;
// 在 s 中寻找窗口大小为 k 时的所包含最大元音字母个数
int left = 0, right = k;
// 初始化固定窗口大小k
for (int i = left; i < right; i++) {
window.add(s[i]);
}
// 初始化完成后,这时已经是一个窗口了,根据条件对窗口做一些事情
// ... 可以计算窗口最大值等
// 使用固定窗口进行遍历
while(right < s.size()) {
window.add(s[right]);
right++;
window.remove(s[left]);
left++;
// 这是已经是一个窗口了,根据条件做一些事情
// ... 可以计算窗口最大值等
}
return res;
}
优化,去除left:
int slidingWindow() {
// 固定窗口大小为 k
string s;
// 在 s 中寻找窗口大小为 k 时的所包含最大元音字母个数
int right = 0;
while(right < s.size()) {
window.add(s[right]);
right++;
// 如果符合要求,说明窗口构造完成,
if (right>=k) {
// 这是已经是一个窗口了,根据条件做一些事情
// ... 可以计算窗口最大值等
// 最后不要忘记把 right -k 位置元素从窗口里面移除
}
}
return res;
}
可以发现此时不需要依赖 left 指针了。因为窗口固定所以其实就没必要使用left,right 双指针来控制窗口的大小。
其次是对于窗口是固定的,可以轻易获取到 left 的位置,此处 left = right - k;
实际上,对于窗口的构造是很重要的。具体可以看下面的实例。
实例1
1208. 尽可能使字符串相等
给你两个长度相同的字符串,s 和 t。
将 s 中的第 i 个字符变到 t 中的第 i 个字符需要 |s[i] - t[i]| 的开销(开销可能为 0),也就是两个字符的 ASCII 码值的差的绝对值。
用于变更字符串的最大预算是 maxCost。在转化字符串时,总开销应当小于等于该预算,这也意味着字符串的转化可能是不完全的。
如果你可以将 s 的子字符串转化为它在 t 中对应的子字符串,则返回可以转化的最大长度。
如果 s 中没有子字符串可以转化成 t 中对应的子字符串,则返回 0。
示例 1:
输入:s = "abcd", t = "bcdf", cost = 3
输出:3
解释:s 中的 "abc" 可以变为 "bcd"。开销为 3,所以最大长度为 3。
示例 2:
输入:s = "abcd", t = "cdef", cost = 3
输出:1
解释:s 中的任一字符要想变成 t 中对应的字符,其开销都是 2。因此,最大长度为 1。
示例 3:
输入:s = "abcd", t = "acde", cost = 0
输出:1
解释:你无法作出任何改动,所以最大长度为 1。
我的
class Solution {
public int equalSubstring(String s, String t, int maxCost) {
char[] sChar = s.toCharArray(), tChar = t.toCharArray();
int left = 0, right = 0;
int maxLength = 0;
while (right < sChar.length) {
// 花费代价
int cost = Math.abs(sChar[right] - tChar[right]);
if (maxCost >= cost) {
maxCost -= cost;
right++;
} else {
maxCost += Math.abs(sChar[left] - tChar[left]);
left++;
}
// 记录最大长度
maxLength = Math.max(maxLength, right - left);
}
return maxLength;
}
}
答案
class Solution {
public int equalSubstring(String s, String t, int maxCost) {
int left = 0, right =0;
int sum = 0;
int res = 0;
// 构造窗口
while (right < s.length()) {
sum += Math.abs(s.charAt(right) - t.charAt(right));
right++;
// 窗口构造完成,这时候要根据条件当前的窗口调整窗口大小
while (sum > maxCost) {
sum -= Math.abs(s.charAt(left) - t.charAt(left));
left++;
}
// 记录此时窗口的大小
res = Math.max(res, right -left);
}
return res;
}
}
这里跟前面总结的框架不一样的一个点就是,前面的框架是求最小窗口大小,这里是求最大窗口大小,大家要学会灵活变通。
239. 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
我的
使用单调队列,队列元素从队头到队尾依次递减,队头元素为当前队列中的最大值
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 辅助队列
LinkedList<Integer> maxQueue = new LinkedList<>();
int left = 0, right = k;
int[] result = new int[nums.length - k + 1];
maxQueue.offer(nums[left]);
for (int i = left + 1; i < right; i++) {
// 入队
while (maxQueue.peekLast() != null && nums[i] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[i]);
}
while (right < nums.length) {
// 右入队,左出队
// 每次出队都获取当前窗口的最大值
result[left] = maxQueue.peekFirst();
if (nums[left] == result[left]) {
maxQueue.poll();
}
while (maxQueue.peekLast() != null && nums[right] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[right]);
right++;
left++;
}
// 将最后一次入队的最大值提出来
result[left] = maxQueue.peekFirst();
return result;
}
}
解答:
前言
对于每个滑动窗口,我们可以使用 \(O(k)\) 的时间遍历其中的每一个元素,找出其中的最大值。对于长度为 n 的数组 \(\textit{nums}\) 而言,窗口的数量为 \(n-k+1\),因此该算法的时间复杂度为 \(O((n-k+1)k)=O(nk)\),会超出时间限制,因此我们需要进行一些优化。
我们可以想到,对于两个相邻(只差了一个位置)的滑动窗口,它们共用着 \(k−1\) 个元素,而只有 1 个元素是变化的。我们可以根据这个特点进行优化。
方法一:优先队列
思路与算法
对于「最大值」,我们可以想到一种非常合适的数据结构,那就是优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
对于本题而言,初始时,我们将数组 \(\textit{nums}\) 的前 k 个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 \(\textit{nums}\) 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 \((\textit{num}, \textit{index})\),表示元素 \(\textit{num}\) 在数组中的下标为 \(\textit{index}\)。
代码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] pair1, int[] pair2) {
return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
for (int i = 0; i < k; ++i) {
pq.offer(new int[]{nums[i], i});
}
int[] ans = new int[n - k + 1];
ans[0] = pq.peek()[0];
for (int i = k; i < n; ++i) {
pq.offer(new int[]{nums[i], i});
while (pq.peek()[1] <= i - k) {
pq.poll();
}
ans[i - k + 1] = pq.peek()[0];
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n \log n)\),其中 n 是数组 \(\textit{nums}\) 的长度。在最坏情况下,数组 \(\textit{nums}\) 中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 \(O(\log n)\),因此总时间复杂度为 \(O(n \log n)\)。
-
空间复杂度:\(O(n)\),即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 \(O(n)\) 空间,只计算额外的空间使用。
方法二:单调队列
思路与算法
我们可以顺着方法一的思路继续进行优化。
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标 i 和 j,其中 i 在 j 的左侧(i < j),并且 i 对应的元素不大于 j 对应的元素(\(\textit{nums}[i] \leq \textit{nums}[j]\)),那么会发生什么呢?
当滑动窗口向右移动时,只要 i 还在窗口中,那么 j 一定也还在窗口中,这是 i 在 j 的左侧所保证的。因此,由于 \(\textit{nums}[j]\) 的存在,\(\textit{nums}[i]\) 一定不会是滑动窗口中的最大值了,我们可以将 \(\textit{nums}[i]\) 永久地移除。
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 \(\textit{nums}\) 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标,它们对应的值相等或者递增,那么令前者为 i,后者为 j,就对应了上面所说的情况,即 \(\textit{nums}[i]\) 会被移除,这就产生了矛盾。
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
由于队列中下标对应的元素是严格单调递减的,因此此时队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是,此时的最大值可能在滑动窗口左边界的左侧,并且随着窗口向右移动,它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素,直到队首元素在窗口中为止。
为了可以同时弹出队首和队尾的元素,我们需要使用双端队列。满足这种单调性的双端队列一般称作「单调队列」。
代码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
Deque`<Integer>` deque = new LinkedList`<Integer>`();
for (int i = 0; i < k; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
}
int[] ans = new int[n - k + 1];
ans[0] = nums[deque.peekFirst()];
for (int i = k; i < n; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
while (deque.peekFirst() <= i - k) {
deque.pollFirst();
}
ans[i - k + 1] = nums[deque.peekFirst()];
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{nums}\) 的长度。每一个下标恰好被放入队列一次,并且最多被弹出队列一次,因此时间复杂度为 \(O(n)\)。
-
空间复杂度:\(O(k)\)。与方法一不同的是,在方法二中我们使用的数据结构是双向的,因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素,因此队列使用的空间为 \(O(k)\)。
这道题难度是困难。当然我们也会发现,这道题目和前面的非固定大小滑动窗口还是不一样的。
看了一道困难的题目后,接下来看一道中等难度的就会发现是小菜一碟。
1456. 定长子串中元音的最大数目
给你字符串 s 和整数 k 。
请返回字符串 s 中长度为 k 的单个子字符串中可能包含的最大元音字母数。
英文中的 元音字母 为(a, e, i, o, u)。
示例 1:
输入:s = "abciiidef", k = 3
输出:3
解释:子字符串 "iii" 包含 3 个元音字母。
示例 2:
输入:s = "aeiou", k = 2
输出:2
解释:任意长度为 2 的子字符串都包含 2 个元音字母。
示例 3:
输入:s = "leetcode", k = 3
输出:2
解释:"lee"、"eet" 和 "ode" 都包含 2 个元音字母。
示例 4:
输入:s = "rhythms", k = 4
输出:0
解释:字符串 s 中不含任何元音字母。
示例 5:
输入:s = "tryhard", k = 4
输出:1
提示:
1 <= s.length <= 10^5
s 由小写英文字母组成
1 <= k <= s.length
我的
class Solution {
public int maxVowels(String s, int k) {
int left = 0, right = k;
int result = 0, max = 0;;
char[] sChar = s.toCharArray();
// 首先遍历固定窗口内的元素
for (int i = left; i < k; i++) {
if (isYuan(sChar[i])) {
result++;
}
max = Math.max(max, result);
}
// 然后移动窗口进行遍历
while (right < s.length()) {
if (isYuan(sChar[right])) {
result++;
}
if (isYuan(sChar[left])) {
result--;
}
max = Math.max(max, result);
right++;
left++;
}
return max;
}
public boolean isYuan(char c) {
return c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u';
}
}
解答
class Solution {
public int maxVowels(String s, int k) {
int right =0;
int sum = 0;
int max = 0;
while (right < s.length()) {
sum += isYuan(s.charAt(right)) ;
right++;
if (right >=k) {
max = Math.max(max, sum);
sum -= isYuan(s.charAt(right-k));
}
}
return max;
}
public int isYuan(char s) {
return s=='a' || s=='e' ||s=='i' ||s=='o' ||s=='u' ? 1:0;
}
}
实例2
剑指 Offer 57 - II. 和为s的连续正数序列(简单)
题目:输入一个正整数 target ,输出所有和为 target 的连续正整数序列(至少含有两个数)。序列内的数字由小到大排列,不同序列按照首个数字从小到大排列。
示例 1:
输入:target = 9
输出:[[2,3,4],[4,5]]
示例 2:
输入:target = 15
输出:[[1,2,3,4,5],[4,5,6],[7,8]]
答案
这个题目比较简单,典型的一道滑动窗口的题目。
假若我们输入的 target 为 9,大脑中应该有下面这么个玩意:

然后我们通过左右指针来维护一个滑动窗口,同时计算窗口内的值是否是目标值:

如果窗口的值过小,我们就移动右边界。

如果窗口的值过大,我们就移动左边界。
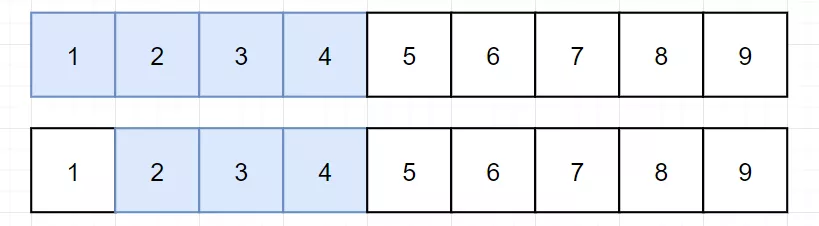
剩下的就是反复上面的操作就可以了。到这里分析过程看似结束了。但是我们可以观察出一丢丢规律,用来优化我们的算法。对于任意一个正整数,总是小于它的中值与中值+1的和。为了让大家直观,用下图举例:

比如这里的100,就一定小于50+51,换成其他数也一样。换句话说,一旦窗口左边界超过中值,窗口内的和一定会大于 target。
根据分析,得到题解:
同时也给一个java版本的:
//java
class Solution {
public int[][] findContinuousSequence(int target) {
List<int[]> res = new ArrayList<>();
int i = 1;
int j = 1;
int win = 0;
while (i <= target / 2) {
if (win < target) {
win += j;
j++;
} else if (win > target) {
win -= i;
i++;
} else {
int[] arr = new int[j-i];
for (int k = i; k < j; k++) {
arr[k-i] = k;
}
res.add(arr);
win -= i;
i++;
}
}
return res.toArray(new int[res.size()][]);
}
}
答案2
什么是滑动窗口
滑动窗口可以看成数组中框起来的一个部分。在一些数组类题目中,我们可以用滑动窗口来观察可能的候选结果。当滑动窗口从数组的左边滑到了右边,我们就可以从所有的候选结果中找到最优的结果。
对于这道题来说,数组就是正整数序列 \([1, 2, 3, \dots, n]\)。我们设滑动窗口的左边界为 i,右边界为 j,则滑动窗口框起来的是一个左闭右开区间 \([i, j)\)。注意,为了编程的方便,滑动窗口一般表示成一个左闭右开区间。在一开始,\(i=1, j=1\),滑动窗口位于序列的最左侧,窗口大小为零。

滑动窗口的重要性质是:窗口的左边界和右边界永远只能向右移动,而不能向左移动。这是为了保证滑动窗口的时间复杂度是 \(O(n)\)。如果左右边界向左移动的话,这叫做“回溯”,算法的时间复杂度就可能不止 \(O(n)\)。
在这道题中,我们关注的是滑动窗口中所有数的和。当滑动窗口的右边界向右移动时,也就是 j = j + 1,窗口中多了一个数字 j,窗口的和也就要加上 j。当滑动窗口的左边界向右移动时,也就是 i = i + 1,窗口中少了一个数字 i,窗口的和也就要减去 i。滑动窗口只有 右边界向右移动(扩大窗口) 和 左边界向右移动(缩小窗口) 两个操作,所以实际上非常简单。
如何用滑动窗口解这道题
要用滑动窗口解这道题,我们要回答两个问题:
- 第一个问题,窗口何时扩大,何时缩小?
- 第二个问题,滑动窗口能找到全部的解吗?
对于第一个问题,回答非常简单:
- 当窗口的和小于 target 的时候,窗口的和需要增加,所以要扩大窗口,窗口的右边界向右移动
- 当窗口的和大于 target 的时候,窗口的和需要减少,所以要缩小窗口,窗口的左边界向右移动
- 当窗口的和恰好等于 target 的时候,我们需要记录此时的结果。设此时的窗口为 \([i, j)\),那么我们已经找到了一个 i 开头的序列,也是唯一一个 i 开头的序列,接下来需要找 i+1 开头的序列,所以窗口的左边界要向右移动
对于第二个问题,我们可以稍微简单地证明一下:

我们一开始要找的是 1 开头的序列,只要窗口的和小于 target,窗口的右边界会一直向右移动。假设 \(1+2+\dots+8\) 小于 target,再加上一个 9 之后, 发现 \(1+2+\dots+8+9\) 又大于 target 了。这说明 1 开头的序列找不到解。此时滑动窗口的最右元素是 9。
接下来,我们需要找 2 开头的序列,我们发现,\(2 + \dots + 8 < 1 + 2 + \dots + 8 < \mathrm{target}\)。这说明 2 开头的序列至少要加到 9。那么,我们只需要把原先 1~9 的滑动窗口的左边界向右移动,变成 2~9 的滑动窗口,然后继续寻找。而右边界完全不需要向左移动。
以此类推,滑动窗口的左右边界都不需要向左移动,所以这道题用滑动窗口一定可以得到所有的解。时间复杂度是 \(O(n)\)。
注:这道题当前可以用等差数列的求和公式来计算滑动窗口的和。不过我这里没有使用求和公式,是为了展示更通用的解题思路。实际上,把题目中的正整数序列换成任意的递增整数序列,这个方法都可以解。
本题题解:
class Solution {
public int[][] findContinuousSequence(int target) {
// 这得从1开始看起
// 如果 滑动窗口的数字和sum == target 那么就可以加入列表,算一个
// 如果大于,那就前进 left,
// 如果小于,前进 right
int left = 1;
int right = 1;
int sum = 0;
List<int[]> list = new ArrayList<>();
// while (right <= target) {
while (left <= target / 2) {
if (sum == target) {
int[] arr = new int[right - left];
for (int i = left; i < right; i++) {
arr[i - left] = i;
}
list.add(arr);
// 通过了就左边界前进,继续遍历
sum -= left;
left++;
} else if (sum < target) {
sum += right;
right++;
} else if (sum > target) {
sum -= left;
left++;
}
}
// return list.toArray(); // 这样是不行的,不然返回的是Object[]数组,得指明数组类型
return list.toArray(new int[list.size()][]);
}
}
3. 无重复字符的最长子串
在上一题中,我们使用双端队列完成了滑动窗口的一道颇为困难的题目,以此展示了什么是滑动窗口。在本节中我们将继续深入分析,探索滑动窗口题型一些具有模式性的解法。
第3题:给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
答案
直接分析题目,假设我们的输入为“abcabcbb”,我们只需要维护一个窗口在输入字符串中进行移动。如下图:
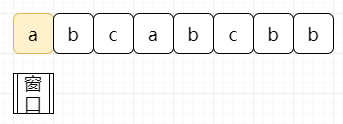
当下一个元素在窗口没有出现过时,我们扩大窗口。
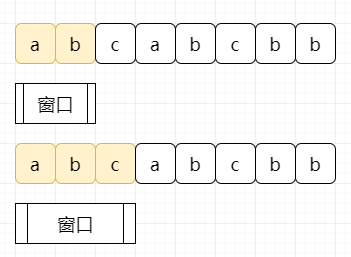
当下一个元素在窗口中出现过时,我们缩小窗口,将出现过的元素以及其左边的元素统统移出:
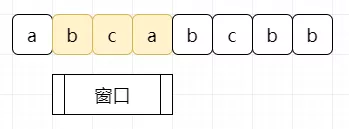
在整个过程中,我们记录下窗口出现过的最大值即可。而我们唯一要做的,只需要尽可能扩大窗口。
那我们代码中通过什么来维护这样的一个窗口呢?anyway~ 不管是队列,双指针,甚至通过map来做,都可以。
我们演示一个双指针的做法:
//java
public class Solution {
public static int lengthOfLongestSubstring(String s) {
int n = s.length();
Set<Character> set = new HashSet<>();
int result = 0, left = 0, right = 0;
while (left < n && right < n) {
//charAt:返回指定位置处的字符
if (!set.contains(s.charAt(right))) {
set.add(s.charAt(right));
right++;
result = Math.max(result, right - left);
} else {
set.remove(s.charAt(left));
left++;
}
}
return result;
}
}

当然,不使用集合,使用哈希表做也是可以的:这里的哈希表键值对是(字符,出现频数)
class Solution {
public int lengthOfLongestSubstring(String s) {
int left = 0;
int right = 0; // 使用右边界来遍历数组
int result = 0; // 用来存放最长子串的长度
char c = 0; // 用来遍历字符串中每个字符
Map<Character, Integer> map = new HashMap<>();
// 前闭后开,滑动窗口
// 每次遍历都添加频度
// 如果不重复就加入哈希表,右边界前进,比较最大长度
// 如果重复,删除哈希表,左边界前进
while (right < s.length()) {
// 使用右边界来遍历数组,后面再判断是否加入哈希表中
c = s.charAt(right);
int count = map.getOrDefault(c, 0) + 1;
if (count > 1) { // 重复,左边界前进,哈希表删除
map.put(s.charAt(left), map.get(s.charAt(left)) - 1);
left++;
} else { // 右边界前进,哈希表增加
map.put(c, count);
right++;
result = result > (right - left)? result : (right - left);
}
}
return result;
}
}
通过观察,我们能看出来。如果是最坏情况的话,我们每一个字符都可能会访问两次,left一次,right一次,时间复杂度达到了O(2N),这是不可饶恕的。不理解的话看下图:
假设我们的字符串为“abcdc”,对于abc我们都访问了2次。
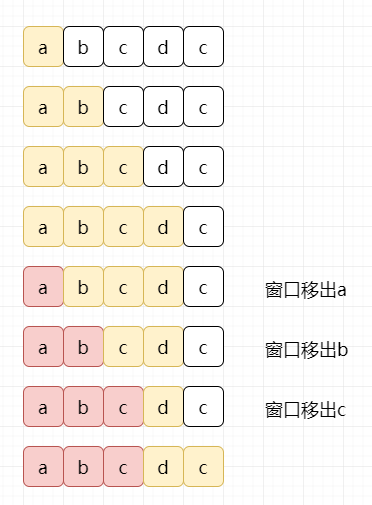
那如何来进一步优化呢?
其实我们可以定义字符到索引的映射,而不是简单通过一个集合来判断字符是否存在。这样的话,当我们找到重复的字符时,我们可以立即跳过该窗口,而不需要对之前的元素进行再次访问。
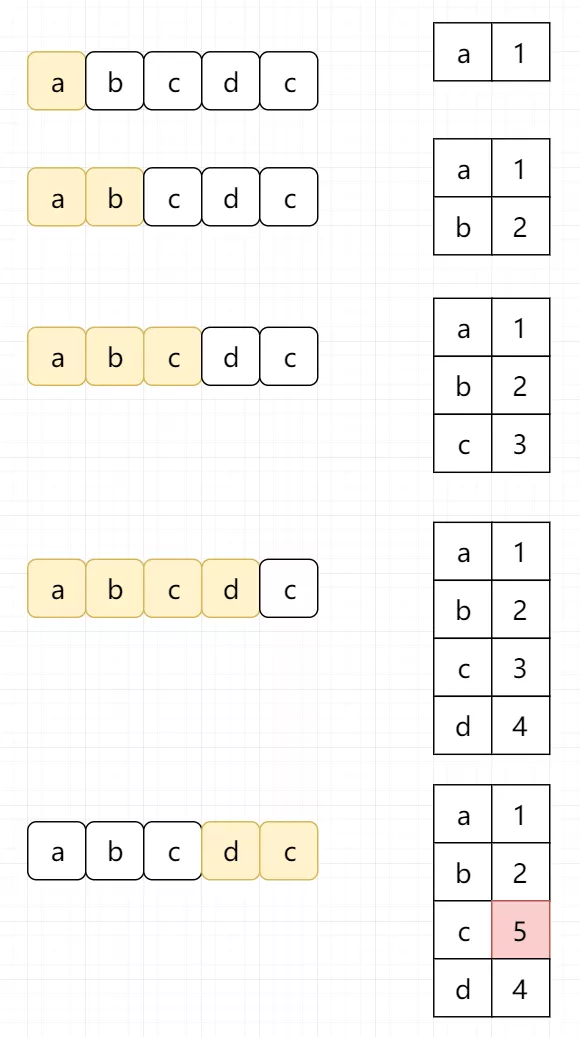
而这里的哈希表的键值对是(字符,字符出现的索引+1)
//java
public class Solution {
public static int lengthOfLongestSubstring(String s) {
int n = s.length(), result = 0;
Map<Character, Integer> map = new HashMap<>();
for (int right = 0, left = 0; right < n; right++) {
if (map.containsKey(s.charAt(right))) {
left = Math.max(map.get(s.charAt(right)), left);
}
result = Math.max(result, right - left + 1);
map.put(s.charAt(right), right + 1);
}
return result;
}
}

我的:
//java
// 上面的哈希表记录的是(字符,频数)
// 这里的哈希表记录的是(字符,出现索引+1)
public class Solution {
public static int lengthOfLongestSubstring(String s) {
int n = s.length(), result = 0;
Map<Character, Integer> map = new HashMap<>();
int left = 0;
int right = 0; // 使用右边界来遍历数组
char c = 0;
while (right < s.length()) {
c = s.charAt(right);
int count = map.getOrDefault(c, -1); // -1代表没有出现过
if (count == -1) { // 没有出现过
map.put(c, right + 1);
right++;
result = Math.max(result, right - left);
} else { // 出现过
left = Math.max(count, left); // 这里需要着重注意,因为滑动窗口left只能前进,不能倒退回去,只能取最大的
map.put(c, right + 1);
right++;
result = Math.max(result, right - left);
}
}
// for (int right = 0, left = 0; right < n; right++) {
// if (map.containsKey(s.charAt(right))) {
// left = Math.max(map.get(s.charAt(right)), left);
// }
// result = Math.max(result, right - left + 1);
// map.put(s.charAt(right), right + 1);
// }
return result;
}
}
修改之后,我们发现虽然时间复杂度有了一定提高,但是还是比较慢!如何更进一步的优化呢?我们可以使用一个256位的数组来替代hashmap,以进行优化。(因为ASCII码表里的字符总共有128个。ASCII码的长度是一个字节,8位,理论上可以表示256个字符,但是许多时候只谈128个。具体原因可以下去自行学习~)
//java
class Solution {
public int lengthOfLongestSubstring(String s) {
int len = s.length();
int result = 0;
int[] charIndex = new int[256];
for (int left = 0, right = 0; right < len; right++) {
char c = s.charAt(right);
left = Math.max(charIndex[c], left);
result = Math.max(result, right - left + 1);
charIndex[c] = right + 1;
}
return result;
}
}

我们发现优化后时间复杂度有了极大的改善!这里简单说一下原因,对于数组和hashmap访问时,两个谁快谁慢不是一定的,需要思考hashmap的底层实现,以及数据量大小。但是在这里,因为已知了待访问数据的下标,可以直接寻址,所以极大的缩短了查询时间。
啰啰嗦嗦
本题基本就到这里。最后要说的,一般建议如果要分析一道题,我们要压缩压缩再压缩,抽茧剥丝一样走到最后,尽可能的完成对题目的优化。不一定非要自己想到最优解,但绝对不要局限于单纯的完成题目,那样将毫无意义!
438. 找到字符串中所有字母异位词
之前的两节讲解了滑动窗口类问题的模式解法,相信大家对该类题型已不陌生。今天将继续完成一道题目,来进行巩固学习。
第438题:给定一个字符串 s 和一个非空字符串 p,找到 s 中所有是 p 的字母异位词的子串,返回这些子串的起始索引。
字符串只包含小写英文字母,并且字符串 s 和 p 的长度都不超过 20100。
说明:
-
字母异位词指字母相同,但排列不同的字符串。
-
不考虑答案输出的顺序。
示例 1:
输入:
s: "cbaebabacd" p: "abc"
输出:
[0, 6]
解释:
起始索引等于 0 的子串是 "cba", 它是 "abc" 的字母异位词。
起始索引等于 6 的子串是 "bac", 它是 "abc" 的字母异位词。
示例 2:
输入:
s: "abab" p: "ab"
输出:
[0, 1, 2]
解释:
起始索引等于 0 的子串是 "ab", 它是 "ab" 的字母异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的字母异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的字母异位词。
答案
直接套用之前的模式,使用双指针来模拟一个滑动窗口进行解题。分析过程如下:
假设我们有字符串为“cbaebabacd”,目标串为“abc”
我们通过双指针维护一个窗口,由于我们只需要判断字母异位词,我们可以将窗口初始化大小和目标串保持一致。(当然,你也可以初始化窗口为1,逐步扩大)
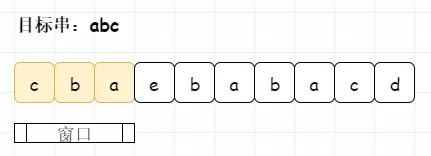
而判断字母异位词,我们需要保证窗口中的字母出现次数与目标串中的字母出现次数一致。这里因为字母只有26个,直接使用数组来替代map进行存储(和上一讲中的ASCII使用256数组存储思想一致)。
pArr为目标串数组,sArr为窗口数组。我们发现初始化数组,本身就满足,记录下来。(这里图示用map模拟数组,便于理解)
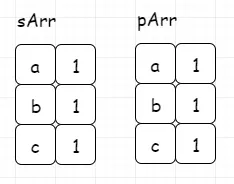
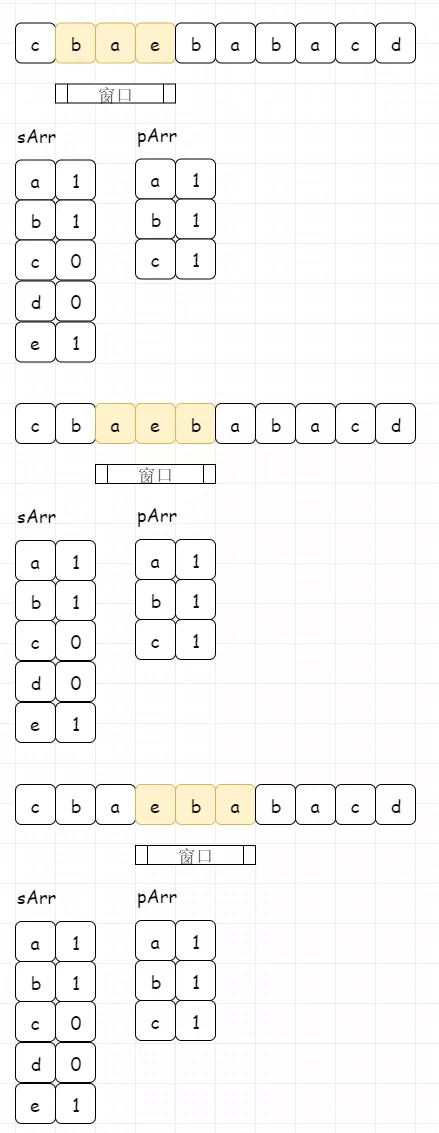
然后我们通过移动窗口,来更新窗口数组,进而和目标数组匹配,匹配成功进行记录。每一次窗口移动,左指针前移,原来左指针位置处的数值减1,表示字母移出;同时右指针前移,右指针位置处的数值加1,表示字母移入。详细过程如下:
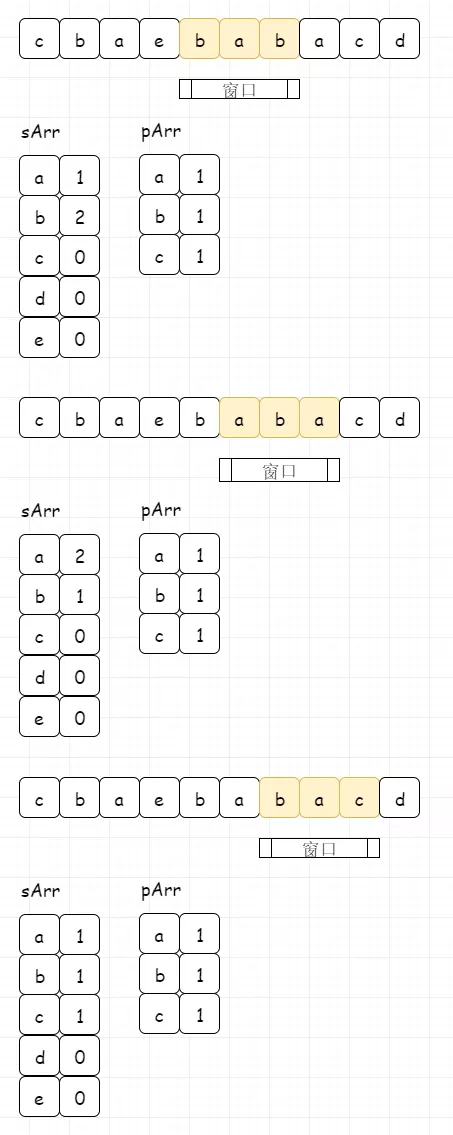
最终,当右指针到达边界,意味着匹配完成。
代码展示
根据分析,完成代码:(下面pSize相关的忽略,调试忘删了)
class Solution {
public List<Integer> findAnagrams(String s, String p) {
if (s == null || p == null || s.length() < p.length()) return new ArrayList<>();
List<Integer> list = new ArrayList<>();
int[] pArr = new int[26];
int pSize = p.length();
int[] sArr = new int[26];
for (int i = 0; i < p.length(); i++) {
sArr[s.charAt(i) - 'a']++;
pArr[p.charAt(i) - 'a']++;
}
for (int i = 0; i < p.length(); i++) {
int index = p.charAt(i) - 'a';
if (pArr[index] == sArr[index])
pSize--;
}
int i = 0;
int j = p.length();
// 窗口大小固定为p的长度
while (j < s.length()) {
if (isSame(pArr, sArr))
list.add(i);
//sArr[s.charAt(i) - 'a']-- 左指针位置处字母减1
sArr[s.charAt(i) - 'a']--;
i++;
//sArr[s.charAt(j) - 'a']++ 右指针位置处字母加1
sArr[s.charAt(j) - 'a']++;
j++;
}
if (isSame( pArr, sArr))
list.add(i);
return list;
}
public boolean isSame(int[] arr1, int[] arr2) {
for (int i = 0; i < arr1.length; ++i)
if (arr1[i] != arr2[i])
return false;
return true;
}
}

我的:
答案一:使用map,超时
class Solution {
public List<Integer> findAnagrams(String s, String p) {
// 固定窗口大小为p.length()
int left = 0;
int right = p.length();
List<Integer> list = new ArrayList<>();
Map<Character, Integer> mapP = new HashMap<>();
Map<Character, Integer> mapS = new HashMap<>();
// 将p的所有字符放入哈希表
for (int i = 0; i < p.length(); i++) {
char c = p.charAt(i);
int count = mapP.getOrDefault(c, 0) + 1;
mapP.put(c, count);
}
while (right <= s.length()) {
// 从left到right,遍历窗口
for (int i = left; i < right; i++) {
char c = s.charAt(i);
int count = mapS.getOrDefault(c, 0) + 1;
mapS.put(c, count);
}
if (mapP.equals(mapS)) {
list.add(left);
}
// 无论如何都要前进
left++;
right++;
// 清理一下mapS,便于下个窗口存入
mapS.clear();
}
return list;
}
}
答案二:上面的算法面对超长超大的字符串会超时,所以我们把哈希表换成了自己写的
// 上面的算法面对超长超大的字符串会超时,所以我们把哈希表换成了自己写的
class Solution {
public List<Integer> findAnagrams(String s, String p) {
int left = 0;
int right = p.length();
int[] mapP = new int[26]; // p的哈希表
int[] mapS = new int[26]; // s的哈希表
List<Integer> list = new ArrayList<>();
// 将p的所有字符放入哈希表
for (int i = 0; i < p.length(); i++) {
mapP[p.charAt(i) - 'a']++;
}
// 由于前闭后开,所以right得等于s.length()才算遍历完了所有
while (right <= s.length()) {
mapS = new int[26];
for (int i = left; i < right; i++) {
mapS[s.charAt(i) - 'a']++;
}
if (isSame(mapP, mapS)) {
list.add(left);
}
left++;
right++;
}
return list;
}
public boolean isSame(int[] mapP, int[] mapS) {
for (int i = 0; i < mapP.length; i++) {
if (mapP[i] != mapS[i]) {
return false;
}
}
return true;
}
}
239. 滑动窗口最大值(困难可不做)
第239题:给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值。
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值所构成的数组。
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
题目分析
本题对于题目没有太多需要额外说明的,应该都能理解,直接进行分析。我们很容易想到,可以通过遍历所有的滑动窗口,找到每一个窗口的最大值,来进行暴力求解。那一共有多少个滑动窗口呢,小学题目,可以得到共有 L-k+1 个窗口。
假设 nums = [1,3,-1,-3,5,3,6,7],和 k = 3,窗口数为6
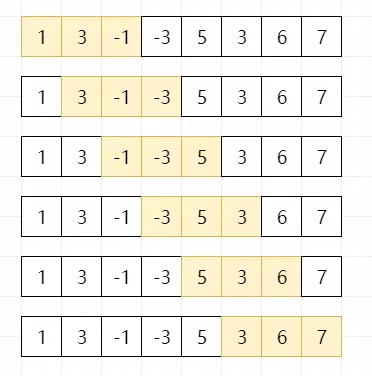
根据分析,直接完成代码:
//java
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int len = nums.length;
if (len * k == 0) return new int[0];
int [] win = new int[len - k + 1];
//遍历所有的滑动窗口
for (int i = 0; i < len - k + 1; i++) {
int max = Integer.MIN_VALUE;
//找到每一个滑动窗口的最大值
for(int j = i; j < i + k; j++) {
max = Math.max(max, nums[j]);
}
win[i] = max;
}
return win;
}
}

It's Bullshit!结果令我们很不满意,时间复杂度达到了O(LK),如果面试问到这道题,基本上只写出这样的代码,一定就挂掉了。那我们怎么样优化时间复杂度呢?有没有可以O(L)的实现呢?=_=
线性题解
这里不卖关子,其实这道题比较经典,我们可以采用队列,DP,堆等方式进行求解,所有思路的主要源头应该都是在窗口滑动的过程中,如何更快的完成查找最大值的过程。但是最典型的解法还是使用双端队列。具体怎么来求解,一起看一下。
首先,我们了解一下,什么是双端队列:是一种具有队列和栈的性质的数据结构。双端队列中的元素可以从两端弹出或者插入。

我们可以利用双端队列来实现一个窗口,目的是让该窗口可以做到张弛有度(汉语博大精深,也就是长度动态变化。其实用游标或者其他解法的目的都是一样的,就是去维护一个可变长的窗口)
然后我们再做一件事,只要遍历该数组,同时在双端队列的头去维护当前窗口的最大值(在遍历过程中,发现当前元素比队列中的元素大,就将原来队列中的元素祭天),在整个遍历的过程中我们再记录下每一个窗口的最大值到结果数组中。最终结果数组就是我们想要的,整体图解如下。
假设 nums = [1,3,-1,-3,5,3,6,7],和 k = 3
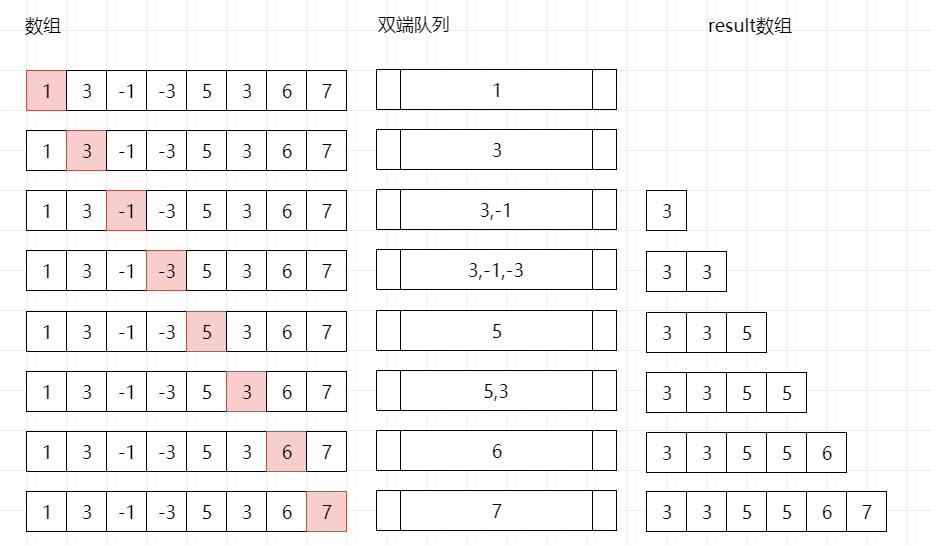
(个人认为我画的这个图是目前全网对于双端队列本题解法比较清晰的一个...所以我觉得如果不点个赞的话...晤..)
根据分析,得出代码:
//go
func maxSlidingWindow(nums []int, k int) []int {
if len(nums) == 0 {
return []int{}
}
//用切片模拟一个双端队列
queue := []int{}
result := []int{}
for i := range nums {
for i > 0 && (len(queue) > 0) && nums[i] > queue[len(queue)-1] {
//将比当前元素小的元素祭天
queue = queue[:len(queue)-1]
}
//将当前元素放入queue中
queue = append(queue, nums[i])
if i >= k && nums[i-k] == queue[0] {
//维护队列,保证其头元素为当前窗口最大值
queue = queue[1:]
}
if i >= k-1 {
//放入结果数组
result = append(result, queue[0])
}
}
return result
}

Perfact题目完成!看着一下子超越百分之99的用户,是不是感觉很爽呢
//Java
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums == null || nums.length < 2) return nums;
// 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数值按从大到小排序
LinkedList<Integer> queue = new LinkedList();
// 结果数组
int[] result = new int[nums.length-k+1];
// 遍历nums数组
for(int i = 0;i < nums.length;i++){
// 保证从大到小 如果前面数小则需要依次弹出,直至满足要求
while(!queue.isEmpty() && nums[queue.peekLast()] <= nums[i]){
queue.pollLast();
}
// 添加当前值对应的数组下标
queue.addLast(i);
// 判断当前队列中队首的值是否有效
if(queue.peek() <= i-k){
queue.poll();
}
// 当窗口长度为k时 保存当前窗口中最大值
if(i+1 >= k){
result[i+1-k] = nums[queue.peek()];
}
}
return result;
}
}
76. 最小覆盖子串
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:
对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
如果 s 中存在这样的子串,我们保证它是唯一的答案。
示例 1:
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
示例 2:
输入:s = "a", t = "a"
输出:"a"
示例 3:
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中,
因此没有符合条件的子字符串,返回空字符串。
提示:
1 <= s.length, t.length <= 105
s 和 t 由英文字母组成
进阶:你能设计一个在 o(n) 时间内解决此问题的算法吗?
我的
这题不愧是困难题,有点意思,右指针不仅作为遍历指针,还要作为边界
class Solution {
public String minWindow(String s, String t) {
Map<Character, Integer> tMap = new HashMap<>();
Map<Character, Integer> winMap = new HashMap<>();
int left = 0, right = 0, minLength = Integer.MAX_VALUE;
char[] sChar = s.toCharArray();
String result = "";
for (char c : t.toCharArray()) {
tMap.put(c, tMap.getOrDefault(c, 0) + 1);
}
// 这题很奇妙,又需要右指针去遍历,又需要窗口去判断去遍历
while (right <= sChar.length) {
// winMap不能覆盖tMap
if (!canOver(winMap, tMap)) {
if (right >= sChar.length) {
break;
}
winMap.put(sChar[right], winMap.getOrDefault(sChar[right], 0) + 1);
right++;
} else {
// 记录最小子串
if (right - left < minLength) {
minLength = right - left;
result = s.substring(left, right);
}
winMap.put(sChar[left], winMap.getOrDefault(sChar[left], 0) - 1);
left++;
}
}
return result;
}
public boolean canOver(Map<Character, Integer> winMap, Map<Character, Integer> tMap) {
for (Map.Entry<Character, Integer> entry : tMap.entrySet()) {
Character key = entry.getKey();
Integer value = entry.getValue();
if (value > winMap.getOrDefault(key, 0)) {
return false;
}
}
return true;
}
}
567. 字符串的排列
给你两个字符串 s1 和 s2 ,写一个函数来判断 s2 是否包含 s1 的排列。如果是,返回 true ;否则,返回 false 。
换句话说,s1 的排列之一是 s2 的 子串 。
示例 1:
输入:s1 = "ab" s2 = "eidbaooo"
输出:true
解释:s2 包含 s1 的排列之一 ("ba").
示例 2:
输入:s1= "ab" s2 = "eidboaoo"
输出:false
提示:
1 <= s1.length, s2.length <= 104
s1 和 s2 仅包含小写字母
我的
比较两个数组是否相同:Arrays.equals(s1Map, winMap)
class Solution {
public boolean checkInclusion(String s1, String s2) {
int[] s1Map = new int[26]; // s1的哈希表
int[] winMap = new int[26]; // 窗口的哈希表
int left = 0, right = s1.length();
char[] s2Char = s2.toCharArray();
// 记录s1的哈希表
for (char c : s1.toCharArray()) {
s1Map[c - 'a']++;
}
while (right <= s2Char.length) {
winMap = new int[26];
for (int i = left; i < right; i++) {
winMap[s2Char[i] - 'a']++;
}
// 窗口的哈希表与s1的哈希表进行对比
if (Arrays.equals(s1Map, winMap)) {
return true;
} else {
left++;
right++;
}
}
return false;
}
}
支配数
给定一个数组与区间,如果在此区间内某个数出现次数不少于k次,那么这个数就是该区间的支配数。
输入:
整数n代表n个元素,整数k代表出现次数
n个元素的数组nums
输出:
拥有支配数的区间的个数
输入:
6 2
1 2 1 2 3 3
输出:
10
// [1,2,1], [1,2,1,2], [1,2,1,2,3], [1,2,1,2,3,3]
// [2,1,2], [2,1,2,3], [2,1,2,3,3]
// [1,2,3,3], [2,3,3], [3,3]
答案
可以看到如果找到了某个支配数,那么包含该区间的后面区间均可算作拥有支配数。
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
int[] nums = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = in.nextInt();
}
int leftIndex = 0, rightIndex = 0;
Map<Integer, Integer> map = new HashMap<>();
int res = 0;
while (rightIndex < n) {
map.put(nums[rightIndex], map.getOrDefault(nums[rightIndex], 0) + 1);
while (map.getOrDefault(nums[rightIndex], 0) >= k) {
res += n - rightIndex;
map.put(nums[leftIndex], map.getOrDefault(nums[leftIndex], 0) - 1);
leftIndex++;
}
rightIndex++;
}
System.out.println(res);
}
}
笔者将不定期更新【考研或就业】的专业相关知识以及自身理解,希望大家能【关注】我。
如果觉得对您有用,请点击左下角的【点赞】按钮,给我一些鼓励,谢谢!
如果有更好的理解或建议,请在【评论】中写出,我会及时修改,谢谢啦!
本文来自博客园,作者:Nemo&
转载请注明原文链接:https://www.cnblogs.com/blknemo/p/14474027.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号