【算法】哈希表法四部曲
哈希表
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
关键码值与地址一一映射
适用场景
适用于关键字与某一值一一对应,即 可使用键值对map,而hashmap是键值对中较好的实现类
适合计数
- 记录一个元素的出现次数
- 记录一个元素的位置
关键词:一一对应
遍历哈希表的四种方式
注意区分下面的方法:
-
map.entrySet() -
map.keySet -
map.values:需要注意这里是values,而不是valueSet,毕竟value值是可以重复的,不是一个集合set -
map.containsKey() -
map.containsValue()
public static void main(String[] args) {
Map<String,String> map=new HashMap<String,String>();
map.put("1", "value1");
map.put("2", "value2");
map.put("3", "value3");
map.put("4", "value4");
// 第一种:普通使用,二次取值
// 遍历键,取出值
System.out.println("\n通过Map.keySet遍历key和value:");
for (String key:map.keySet()) {
System.out.println("Key: "+key+" Value: "+map.get(key));
}
// 第二种
// 遍历value
System.out.println("\n通过Map.values()遍历所有的value,但不能遍历key");
// 需要注意这里是values,而不是valueSet,毕竟value值是可以重复的,不是一个集合set
for (String v:map.values()) {
System.out.println("The value is "+v);
}
// 第三种:推荐,尤其是容量大时
// foreach
System.out.println("\n通过Map.entrySet遍历key和value");
// Set<Map.Entry<Character, Integer>> map.entrySet()
for (Map.Entry<String, String> entry: map.entrySet()) {
System.out.println("Key: "+ entry.getKey()+ " Value: "+entry.getValue());
}
// 第四种,只有单列集合Collection才有迭代器,所以Map可以转化为Set再迭代
// 使用Map.entrySet()的迭代器
System.out.println("\n通过Map.entrySet使用iterator遍历key和value: ");
Iterator map1it=map.entrySet().iterator();
while (map1it.hasNext()) {
Map.Entry<String, String> entry=(Entry<String, String>) map1it.next();
System.out.println("Key: "+entry.getKey()+" Value: "+entry.getValue());
}
}
输出结果:
通过Map.keySet遍历key和value:
Key: 1 Value: value1
Key: 2 Value: value2
Key: 3 Value: value3
Key: 4 Value: value4
通过Map.values()遍历所有的value,但不能遍历key
The value is value1
The value is value2
The value is value3
The value is value4
通过Map.entrySet使用iterator遍历key和value:
Key: 1 Value: value1
Key: 2 Value: value2
Key: 3 Value: value3
Key: 4 Value: value4
通过Map.entrySet遍历key和value
Key: 1 Value: value1
Key: 2 Value: value2
Key: 3 Value: value3
Key: 4 Value: value4
【推荐】使用entrySet()遍历Map类集合KV,而不是keySet方式进行遍历。
说明:keySet 其实是遍历了2次,一次是转为Iterator对象,另一次是从hashMap中取出key所对应的value。而entrySet只是遍历了一次就把key和value都放到了entry中,效率更高。如果是JDK8,使用Map.foreach方法。
正例:values()返回的是V值集合,是一个list集合对象; keySet()返回的是K值集合,是一个Set集合对象; entrySet()返回的是K-V值组合集合。
记录数组中元素出现频数
遍历nums1,使用哈希表存储关键字,以及他们出现的次数
方法一:遇到空的就赋初值,非空就+1
// 1. 遍历nums1,使用哈希表存储关键字,以及他们出现的次数
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums1.length; i++) {
if (map.get(nums1[i]) != null) {
map.put(nums1[i], map.get(nums1[i])+1);
} else {
map.put(nums1[i], 1);
}
}
方法二:使用getOrDefault()
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for (int num : nums1) {
int count = map.getOrDefault(num, 0) + 1;
map.put(num, count);
}
方法三:如果元素固定,那么我们可以就使用一个一维数组new int[128]来存储他们出现的频数。这也是哈希表法。
遍历字符串 s,记录字符频数
元素固定为字母
int[] map = new int[26]; // 26个字母时
for (int i = 0; i < s.length(); i++) {
map[s.charAt(i) - 'a']++;
}
// 或者
for (char c : s.toCharArray()) {
map[c - 'a']++;
}
元素固定为字符,ASCII码128个字符
int[] map = new int[128]; // 所有ASCII码字符128个
for (int i = 0; i < s.length(); i++) {
map[s.charAt(i)]++;
}
// 或者
for (char c : s.toCharArray()) {
map[c]++;
}
方法四:如果要求元素只出现一次 或者判断是否有重复元素,那就可以用哈希集合
Set<Integer, Integer> set = new HashSet<Integer>();
for (int num : nums1) {
// 添加此元素至 Set,加入失败那就代表有重复
if(!set.add(num)) {
return false;
}
}
哈希表 + 列表
哈希表 = <String, ArrayList>,键值对为<字符串, 列表>
for (int i = 0; i < p.length(); i++) {
if (!map.containsKey(keyStr)) { // 如果不存在此键
map.put(keyStr, new ArrayList<>()); // 创建一个列表
}
map.get(keyStr).add(s); // 获取此键对应的列表,添加列表元素
}
面试题 10.02. 变位词组
编写一种方法,对字符串数组进行排序,将所有变位词组合在一起。变位词是指字母相同,但排列不同的字符串。
注意:本题相对原题稍作修改
示例:
输入: ["eat", "tea", "tan", "ate", "nat", "bat"],
输出:
[
["ate","eat","tea"],
["nat","tan"],
["bat"]
]
我的
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<>();
for (int i = 0; i < strs.length; i++) {
int[] set = new int[26];
for (char c : strs[i].toCharArray()) {
set[c - 'a']++;
}
StringBuilder sb = new StringBuilder();
for (int s = 0; s < set.length; s++) {
sb.append('a' + s);
sb.append(set[s]);
}
String key = sb.toString();
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(strs[i]);
map.put(key, list);
}
List<List<String>> result = new ArrayList<>();
for (Map.Entry<String, List<String>> entry : map.entrySet()) {
result.add(entry.getValue());
}
return result;
}
}
答案
用哈希表来存储列表,使字符串与列表一一对应。
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String, List<String>> map = new HashMap<String, List<String>>();
for (String str : strs) {
int[] counts = new int[26];
int length = str.length();
for (int i = 0; i < length; i++) {
counts[str.charAt(i) - 'a']++;
}
// 将每个出现次数大于 0 的字母和出现次数按顺序拼接成字符串,作为哈希表的键
StringBuffer sb = new StringBuffer();
for (int i = 0; i < 26; i++) {
if (counts[i] != 0) {
sb.append((char) ('a' + i));
sb.append(counts[i]);
}
}
String key = sb.toString();
List<String> list = map.getOrDefault(key, new ArrayList<String>());
list.add(str);
map.put(key, list);
}
return new ArrayList<List<String>>(map.values());
}
}
实例
383. 赎金信
给你两个字符串:ransomNote 和 magazine ,判断 ransomNote 能不能由 magazine 里面的字符构成。
如果可以,返回 true ;否则返回 false 。
magazine 中的每个字符只能在 ransomNote 中使用一次。
示例 1:
输入:ransomNote = "a", magazine = "b"
输出:false
示例 2:
输入:ransomNote = "aa", magazine = "ab"
输出:false
示例 3:
输入:ransomNote = "aa", magazine = "aab"
输出:true
答案
class Solution {
public boolean canConstruct(String ransomNote, String magazine) {
if (ransomNote.length() > magazine.length()) {
return false;
}
int[] cnt = new int[26];
for (char c : magazine.toCharArray()) {
cnt[c - 'a']++;
}
for (char c : ransomNote.toCharArray()) {
cnt[c - 'a']--;
if(cnt[c - 'a'] < 0) {
return false;
}
}
return true;
}
}
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
答案
class Solution {
public int[] twoSum(int[] nums, int target) {
// 哈希表用来存放(关键字,下标)
Map<Integer, Integer> map = new HashMap<>();
// 遍历数组,每次遇到一个元素判断哈希表里面有没有与其对应的target - nums[i]元素
// 如果有就返回下标,如果没有就把它的关键字和下标放进去,
for (int i = 0; i < nums.length; i++) {
Integer index = map.get(target - nums[i]);
if (index != null) {
return new int[]{index, i};
} else {
map.put(nums[i], i);
}
}
return null;
}
}
面试题 16.24. 数对和
设计一个算法,找出数组中两数之和为指定值的所有整数对。一个数只能属于一个数对。
示例 1:
输入: nums = [5,6,5], target = 11
输出: [[5,6]]
示例 2:
输入: nums = [5,6,5,6], target = 11
输出: [[5,6],[5,6]]
答案一:两次遍历
遇到这题的第一反应就是,先哈希表确定每个元素的出现次数,再来找匹配的元素。
class Solution {
public List<List<Integer>> pairSums(int[] nums, int target) {
//key:数组的元素;value:该元素出现的次数
Map<Integer, Integer> map = new HashMap<>();
List<List<Integer>> res = new ArrayList<>();
for (int i = 0; i < nums.length; i++) {
int count = map.getOrDefault(nums[i], 0) + 1;
map.put(nums[i], count);
}
for (int i = 0; i < nums.length; i++) {
int count1 = map.getOrDefault(nums[i], 0);
map.put(nums[i], count1 - 1);
int count2 = map.getOrDefault(target - nums[i], 0);
map.put(target - nums[i], count2 - 1);
if (count1 > 0 && count2 > 0) {
List<Integer> temp = new ArrayList<>();
temp.add(nums[i]);
temp.add(target - nums[i]);
res.add(temp);
}
}
return res;
}
}
答案二:一次遍历
后来我们开始思考,能不能边遍历边寻找匹配的元素呢?
其实我们可以在遍历的时候,直接看有没有匹配的
- 如果有,那就匹配的那个元素-1,当前元素就不+1了,+1-1抵消了
- 如果没有,那就当前元素+1
class Solution {
public List<List<Integer>> pairSums(int[] nums, int target) {
//key:数组的元素;value:该元素出现的次数
Map<Integer, Integer> map = new HashMap<>();
List<List<Integer>> res = new ArrayList<>();
for (int num : nums) {
// 在遍历的时候,直接看有没有匹配的
// 如果有,那就匹配的那个元素-1
// 如果没有,那就当前元素+1
int count = map.getOrDefault(target - num, 0);
if (count > 0) {
res.add(Arrays.asList(num, target - num));
map.put(target - num, --count);
} else {
map.put(num, map.getOrDefault(num, 0) + 1);
}
}
return res;
}
}
有效的字母异位词
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
示例 1:
输入: s = "anagram", t = "nagaram"
输出: true
示例 2:
输入: s = "rat", t = "car"
输出: false
说明:
你可以假设字符串只包含小写字母。
进阶:
如果输入字符串包含 unicode 字符怎么办?你能否调整你的解法来应对这种情况?
方法一:排序
t 是 s 的异位词等价于「两个字符串排序后相等」。因此我们可以对字符串 s 和 t 分别排序,看排序后的字符串是否相等即可判断。此外,如果 s 和 t 的长度不同,t 必然不是 s 的异位词。
Java
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
char[] str1 = s.toCharArray();
char[] str2 = t.toCharArray();
Arrays.sort(str1);
Arrays.sort(str2);
return Arrays.equals(str1, str2);
}
}
复杂度分析
-
时间复杂度:\(O(n \log n)\),其中 n 为 s 的长度。排序的时间复杂度为 \(O(n\log n)\),比较两个字符串是否相等时间复杂度为 \(O(n)\),因此总体时间复杂度为 \(O(n \log n+n)=O(n\log n)\)。
-
空间复杂度:\(O(\log n)\)。排序需要 \(O(\log n)\) 的空间复杂度。注意,在某些语言(比如 Java & JavaScript)中字符串是不可变的,因此我们需要额外的 \(O(n)\) 的空间来拷贝字符串。但是我们忽略这一复杂度分析,因为:
这依赖于语言的细节;
这取决于函数的设计方式,例如,可以将函数参数类型更改为 char[]。
方法二:哈希表
前面我们说过了关键码值与地址一一映射,就可以称为哈希表(即 散列表),所以此处的方法也可以称为哈希表法。
从另一个角度考虑,t 是 s 的异位词等价于「两个字符串中字符出现的种类和次数均相等」。由于字符串只包含 26 个小写字母,因此我们可以维护一个长度为 26 的频次数组 \(\textit{table}\),先遍历记录字符串 s 中字符出现的频次,然后遍历字符串 t,减去 \(\textit{table}\) 中对应的频次,如果出现 \(\textit{table}[i]<0\),则说明 t 包含一个不在 s 中的额外字符,返回 \(\text{false}\) 即可。
Java
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
int[] table = new int[26];
for (int i = 0; i < s.length(); i++) {
table[s.charAt(i) - 'a']++;
}
for (int i = 0; i < t.length(); i++) {
table[t.charAt(i) - 'a']--;
if (table[t.charAt(i) - 'a'] < 0) {
return false;
}
}
return true;
}
}
对于进阶问题,\(\text{Unicode}\) 是为了解决传统字符编码的局限性而产生的方案,它为每个语言中的字符规定了一个唯一的二进制编码。而 \(\text{Unicode}\) 中可能存在一个字符对应多个字节的问题,为了让计算机知道多少字节表示一个字符,面向传输的编码方式的 \(\text{UTF}-8\) 和 \(\text{UTF}-16\) 也随之诞生逐渐广泛使用,具体相关的知识读者可以继续查阅相关资料拓展视野,这里不再展开。
回到本题,进阶问题的核心点在于「字符是离散未知的」,因此我们用哈希表维护对应字符的频次即可。同时读者需要注意 \(\text{Unicode}\) 一个字符可能对应多个字节的问题,不同语言对于字符串读取处理的方式是不同的。
Java
class Solution {
public boolean isAnagram(String s, String t) {
if (s.length() != t.length()) {
return false;
}
Map<Character, Integer> table = new HashMap<Character, Integer>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
table.put(ch, table.getOrDefault(ch, 0) + 1);
}
for (int i = 0; i < t.length(); i++) {
char ch = t.charAt(i);
table.put(ch, table.getOrDefault(ch, 0) - 1);
if (table.get(ch) < 0) {
return false;
}
}
return true;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 为 s 的长度。
-
空间复杂度:\(O(S)\),其中 S 为字符集大小,此处 \(S=26\)。
剑指 Offer 61. 扑克牌中的顺子
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2~10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为 0 ,可以看成任意数字。A 不能视为 14。
示例 1:
输入: [1,2,3,4,5]
输出: True
示例 2:
输入: [0,0,1,2,5]
输出: True
我的
class Solution {
public boolean isStraight(int[] nums) {
int[] map = new int[14];
int min = 14, max = -1;
for (int num : nums) {
if (num == 0) {
continue;
}
if (map[num] > 0) {
return false;
}
map[num]++;
min = min < num ? min : num;
max = max > num ? max : num;
}
return max - min + 1 <= 5;
}
}
答案
class Solution {
public boolean isStraight(int[] nums) {
Set<Integer> repeat = new HashSet<>();
int max = 0, min = 14;
for(int num : nums) {
if(num == 0) continue; // 跳过大小王
max = Math.max(max, num); // 最大牌
min = Math.min(min, num); // 最小牌
// 添加此牌至 Set,加入失败那就代表有重复
if(!repeat.add(num)) return false; // 若有重复,提前返回 false
}
return max - min + 1 <= 5; // 最大牌 - 最小牌 + 1 <= 5 则可构成顺子,因为包含有0、0、0、9、11的情况
}
}
面试题 01.04. 回文排列
给定一个字符串,编写一个函数判定其是否为某个回文串的排列之一。
回文串是指正反两个方向都一样的单词或短语。排列是指字母的重新排列。
回文串不一定是字典当中的单词。
示例1:
输入:"tactcoa"
输出:true(排列有"tacocat"、"atcocta",等等)
答案
主要利用函数统计出s中所有重复次数为奇数次元素的个数,如果个数为1或0,则该字符串是一个回文串,否则就不是
class Solution {
public boolean canPermutePalindrome(String s) {
char[] map = new char[128]; // 这里需要存储整个ASCII字符,所以128
int ans = 0;
// for (int i = 0; i < s.length(); i++) {
// map[s.charAt(i)]++;
// }
for (char c : s.toCharArray()) {
map[c]++;
}
for (int i = 0; i < map.length; i++) {
if (map[i] % 2 == 1) {
ans++;
}
}
return ans <= 1;
}
}
剑指 Offer 48. 最长不含重复字符的子字符串
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
哈希表记录元素位置
class Solution {
public int lengthOfLongestSubstring(String s) {
int res = 0;
int leftIndex = 0, rightIndex = 0;
Map<Character, Integer> map = new HashMap<>();
while (rightIndex < s.length()) {
char chr = s.charAt(rightIndex);
Integer index = map.get(chr);
if (index == null) {
map.put(chr, rightIndex);
} else {
if (index >= leftIndex) {
leftIndex = index + 1;
}
map.put(chr, rightIndex);
}
rightIndex++;
res = Math.max(res, rightIndex - leftIndex);
}
return res;
}
}
class Solution {
public int lengthOfLongestSubstring(String s) {
char[] chars = s.toCharArray();
// 存放元素和其对应下标
Map<Character, Integer> map = new HashMap<>();
int left = 0, right = 0, res = 0;
while (right < chars.length) {
Integer index = map.get(chars[right]);
if (index == null) {
map.put(chars[right], right);
right++;
} else {
if (index >= left) {
left = index + 1;
}
map.remove(chars[index]);
}
res = Math.max(res, right - left);
}
return res;
}
}
128. 最长连续序列
给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素在原数组中连续)的长度。
请你设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入:nums = [100,4,200,1,3,2]
输出:4
解释:最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。
示例 2:
输入:nums = [0,3,7,2,5,8,4,6,0,1]
输出:9
哈希表
我们考虑枚举数组中的每个数 x,考虑以其为起点,不断尝试匹配 x+1,x+2,⋯ 是否存在,假设最长匹配到了 x+y,那么以 x 为起点的最长连续序列即为 x,x+1,x+2,⋯,x+y,其长度为 y+1,我们不断枚举并更新答案即可。
对于匹配的过程,暴力的方法是 \(O(n)\) 遍历数组去看是否存在这个数,但其实更高效的方法是用一个哈希表存储数组中的数,这样查看一个数是否存在即能优化至 \(O(1)\) 的时间复杂度。
仅仅是这样我们的算法时间复杂度最坏情况下还是会达到 \(O(n^2)\)(即外层需要枚举 \(O(n)\) 个数,内层需要暴力匹配 \(O(n)\) 次),无法满足题目的要求。但仔细分析这个过程,我们会发现其中执行了很多不必要的枚举,如果已知有一个 x,x+1,x+2,⋯,x+y 的连续序列,而我们却重新从 x+1,x+2 或者是 x+y 处开始尝试匹配,那么得到的结果肯定不会优于枚举 x 为起点的答案,因此我们在外层循环的时候碰到这种情况跳过即可。
那么怎么判断是否跳过呢?由于我们要枚举的数 x 一定是在数组中不存在前驱数 x-1 的,不然按照上面的分析我们会从 x-1 开始尝试匹配,因此我们每次在哈希表中检查是否存在 x-1 即能判断是否需要跳过了。
增加了判断跳过的逻辑之后,时间复杂度是多少呢?外层循环需要 \(O(n)\) 的时间复杂度,只有当一个数是连续序列的第一个数的情况下才会进入内层循环,然后在内层循环中匹配连续序列中的数,因此数组中的每个数只会进入内层循环一次。根据上述分析可知,总时间复杂度为 \(O(n)\),符合题目要求。
class Solution {
public int longestConsecutive(int[] nums) {
Set<Integer> set = new HashSet<>();
// 遍历一遍加入集合
for (int num : nums) {
set.add(num);
}
int res = 0;
// 重新遍历一遍
// 找到序列最开头的数字num(没有前驱num - 1的那个数字)后
// 继续 num + 1看序列最长有多长
for (int num : nums) {
if (set.contains(num - 1)) {
continue;
}
int tempRes = 0;
while (set.contains(num++)) {
tempRes++;
}
res = Math.max(res, tempRes);
}
return res;
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 为数组的长度。具体分析已在上面正文中给出。
- 空间复杂度:\(O(n)\)。哈希表存储数组中所有的数需要 \(O(n)\) 的空间。
146. LRU 缓存
请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以 正整数 作为容量capacity初始化 LRU 缓存int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回 -1 。void put(int key, int value)如果关键字key已经存在,则变更其数据值value;如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
示例:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
自带容器
实现本题的两种操作,需要用到一个哈希表和一个双向链表。在面试中,面试官一般会期望读者能够自己实现一个简单的双向链表,而不是使用语言自带的、封装好的数据结构。在 Python 语言中,有一种结合了哈希表与双向链表的数据结构 OrderedDict,只需要短短的几行代码就可以完成本题。在 Java 语言中,同样有类似的数据结构 LinkedHashMap。这些做法都不会符合面试官的要求,因此下面只给出使用封装好的数据结构实现的代码,而不多做任何阐述。
class LRUCache extends LinkedHashMap<Integer, Integer>{
private int capacity;
public LRUCache(int capacity) {
super(capacity, 0.75F, true);
this.capacity = capacity;
}
public int get(int key) {
return super.getOrDefault(key, -1);
}
public void put(int key, int value) {
super.put(key, value);
}
@Override
protected boolean removeEldestEntry(Map.Entry<Integer, Integer> eldest) {
return size() > capacity;
}
}
哈希表 + 双向链表
算法
LRU 缓存机制可以通过哈希表辅以双向链表实现,我们用一个哈希表和一个双向链表维护所有在缓存中的键值对。
- 双向链表按照被使用的顺序存储了这些键值对,靠近头部的键值对是最近使用的,而靠近尾部的键值对是最久未使用的。
- 哈希表即为普通的哈希映射(HashMap),通过缓存数据的键映射到其在双向链表中的位置。
这样以来,我们首先使用哈希表进行定位,找出缓存项在双向链表中的位置,随后将其移动到双向链表的头部,即可在 \(O(1)\) 的时间内完成 get 或者 put 操作。具体的方法如下:
-
对于 get 操作,首先判断 key 是否存在:
- 如果 key 不存在,则返回 -1;
- 如果 key 存在,则 key 对应的节点是最近被使用的节点。通过哈希表定位到该节点在双向链表中的位置,并将其移动到双向链表的头部,最后返回该节点的值。
-
对于 put 操作,首先判断 key 是否存在:
- 如果 key 不存在,使用 key 和 value 创建一个新的节点,在双向链表的头部添加该节点,并将 key 和该节点添加进哈希表中。然后判断双向链表的节点数是否超出容量,如果超出容量,则删除双向链表的尾部节点,并删除哈希表中对应的项;
- 如果 key 存在,则与 get 操作类似,先通过哈希表定位,再将对应的节点的值更新为 value,并将该节点移到双向链表的头部。
上述各项操作中,访问哈希表的时间复杂度为 \(O(1)\),在双向链表的头部添加节点、在双向链表的尾部删除节点的复杂度也为 \(O(1)\)。而将一个节点移到双向链表的头部,可以分成「删除该节点」和「在双向链表的头部添加节点」两步操作,都可以在 \(O(1)\) 时间内完成。
小贴士:在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
- FAQ:双向链表的节点只存value不就可以了吗?为什么要存一组key-value,感觉key只在HashMap中就可以了吧?
因为在超出capacity要删除hashmap里key-value时,必须要通过Node里的key来删除,hashmap无法直接通过value来删除。- 为什么要单独实现双向链表呢?为什么不直接使用LinkedList呢?
因为LinkedList容器无法对哈希表所映射的某个具体的节点进行操作,还得从容器中从头到尾遍历一遍,才能找到那个节点,这样时间复杂度就不为\(O(1)\)了。
public class LRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() {}
public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
}
private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();
private int size;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if (node == null) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到头部
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode newNode = new DLinkedNode(key, value);
// 添加进哈希表
cache.put(key, newNode);
// 添加至双向链表的头部
addToHead(newNode);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的尾部节点
DLinkedNode tail = removeTail();
// 删除哈希表中对应的项
cache.remove(tail.key);
--size;
}
} else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到头部
node.value = value;
moveToHead(node);
}
}
private void addToHead(DLinkedNode node) {
node.prev = head;
node.next = head.next;
head.next.prev = node;
head.next = node;
}
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void moveToHead(DLinkedNode node) {
removeNode(node);
addToHead(node);
}
private DLinkedNode removeTail() {
DLinkedNode res = tail.prev;
removeNode(res);
return res;
}
}
复杂度分析
- 时间复杂度:对于 put 和 get 都是 \(O(1)\)。
- 空间复杂度:\(O(\text{capacity})\),因为哈希表和双向链表最多存储 \(\text{capacity} + 1\) 个元素。
我的
小贴士:在双向链表的实现中,使用一个伪头部(dummy head)和伪尾部(dummy tail)标记界限,这样在添加节点和删除节点的时候就不需要检查相邻的节点是否存在。
FAQ:
- 为什么使用双向链表而不是单向链表?
双向链表的作用主要是,在get操作如果访问的是一个处于链表中间位置的节点时,可以获取其前一个节点和后一个节点,从而省略了迭代去查找的时间。- 双向链表的节点只存value不就可以了吗?为什么要存一组key-value,感觉key只在HashMap中就可以了吧?
因为在超出capacity要删除hashmap里key-value时,必须要通过Node里的key来删除,hashmap无法直接通过value来删除。- 为什么要单独实现双向链表呢?为什么不直接使用LinkedList呢?
因为LinkedList容器无法对哈希表所映射的某个具体的节点进行操作,还得从容器中从头到尾遍历一遍,才能找到那个节点,这样时间复杂度就不为\(O(1)\)了。
我这里是按照队列来写的,双向链表的队头代表旧节点,队尾代表新入队的节点。
public class LRUCache {
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
public DLinkedNode() {}
public DLinkedNode(int _key, int _value) {key = _key; value = _value;}
}
private Map<Integer, DLinkedNode> map;
private DLinkedNode head, tail;
private int size;
private int capacity;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
map = new HashMap<Integer, DLinkedNode>();
// 双向链表使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = map.get(key);
if (node == null) {
return -1;
}
// 如果 key 存在,先通过哈希表定位,再移到尾部
moveToTail(node);
return node.value;
}
public void put(int key, int value) {
// 先找哈希表确定节点
DLinkedNode node = map.get(key);
if (node == null) {
// 如果 key 不存在,创建一个新的节点
DLinkedNode newNode = new DLinkedNode(key, value);
// 添加进哈希表
map.put(key, newNode);
// 添加至双向链表的尾部
addToTail(newNode);
++size;
if (size > capacity) {
// 如果超出容量,删除双向链表的头部节点
// 这里如果超出容量,我们需要借助双向链表中的节点的key来找到对应的哈希表项
DLinkedNode head = removeHead();
// 删除哈希表中对应的项
map.remove(head.key);
--size;
}
} else {
// 如果 key 存在,先通过哈希表定位,再修改 value,并移到尾部
node.value = value;
moveToTail(node);
}
}
private void addToTail(DLinkedNode node) {
node.next = tail;
node.prev = tail.prev;
node.next.prev = node;
node.prev.next = node;
}
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
}
private void moveToTail(DLinkedNode node) {
removeNode(node);
addToTail(node);
}
private DLinkedNode removeHead() {
DLinkedNode res = head.next;
removeNode(res);
return res;
}
}
41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
示例 2:
输入:nums = [3,4,-1,1]
输出:2
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
哈希表(空间复杂度不符合要求)
- 按照刚才我们读例子的思路,其实我们只需从最小的正整数 1 开始,依次判断 2、3、4 直到数组的长度 N 是否在数组中;
- 如果当前考虑的数不在这个数组中,我们就找到了这个缺失的最小正整数;
- 由于我们需要依次判断某一个正整数是否在这个数组里,我们可以先把这个数组中所有的元素放进哈希表。接下来再遍历的时候,就可以以 \(O(1)\) 的时间复杂度判断某个正整数是否在这个数组;
- 由于题目要求我们只能使用常数级别的空间,而哈希表的大小与数组的长度是线性相关的,因此空间复杂度不符合题目要求。
public class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
Set<Integer> hashSet = new HashSet<>();
for (int num : nums) {
hashSet.add(num);
}
for (int i = 1; i <= len ; i++) {
if (!hashSet.contains(i)){
return i;
}
}
return len + 1;
}
}
复杂度分析:
- 时间复杂度:\(O(N)\),这里 N 表示数组的长度。第 1 次遍历了数组,第 2 次遍历了区间 [1, len] 里的元素。
- 空间复杂度:\(O(N)\),把 N 个数存在哈希表里面,使用了 N 个空间。
原地哈希(将数组视为哈希表)
原地哈希就相当于,让每个数字n都回到下标为n-1的家里。
而那些没有回到家里的就成了孤魂野鬼流浪在外,他们要么是根本就没有自己的家(数字小于等于0或者大于nums.size()),要么是自己的家被别人占领了(出现了重复)。
这些流浪汉被临时安置在下标为i的空房子里,之所以有空房子是因为房子i的主人i+1失踪了(数字i+1缺失)。
因此通过原地构建哈希让各个数字回家,我们就可以找到原始数组中重复的数字还有消失的数字。
最早知道这个思路是在《剑指 Offe》这本书上看到的,感兴趣的朋友不妨做一下这道问题:剑指 Offer 03. 数组中重复的数字。下面简要叙述:
- 由于题目要求我们「只能使用常数级别的空间」,而要找的数一定在 [1, N + 1] 左闭右闭(这里 N 是数组的长度)这个区间里。因此,我们可以就把原始的数组当做哈希表来使用。事实上,哈希表其实本身也是一个数组;
- 我们要找的数就在 [1, N + 1] 里,最后 N + 1 这个元素我们不用找。因为在前面的 N 个元素都找不到的情况下,我们才返回 N + 1;
- 所以我们需要将 [0, N]的数组下标 与 [1, N + 1]的数哈希算法应该为
- 那么,我们可以采取这样的思路:就把 1 这个数放到下标为 0 的位置,2 这个数放到下标为 1 的位置,按照这种思路整理一遍数组。然后我们再遍历一次数组,第 1 个遇到的它的值不等于下标的那个数,就是我们要找的缺失的第一个正数。
- 这个思想就相当于我们自己编写哈希函数,这个哈希函数的规则特别简单,那就是数值为 i 的数映射到下标为 i - 1 的位置。
注意下面的nums[nums[i] - 1] != nums[i],很关键
public class Solution {
public int firstMissingPositive(int[] nums) {
int len = nums.length;
for (int i = 0; i < len; i++) {
// 注意理解这里的 nums[nums[i] - 1] != nums[i]
// 如果不加最外层的nums[],而采用 nums[i] - 1 != i 可能会陷入死循环
// 如果要使用nums[i] - 1 != i,也可以在里面加一层if,判断nums[nums[i] - 1] == nums[i]就跳出循环
while (nums[i] > 0 && nums[i] <= len && nums[nums[i] - 1] != nums[i]) {
// 满足在指定范围内、并且没有放在正确的位置上,才交换
// 例如:数值 3 应该放在索引 2 的位置上
swap(nums, nums[i] - 1, i);
}
}
// [1, -1, 3, 4]
for (int i = 0; i < len; i++) {
if (nums[i] != i + 1) {
return i + 1;
}
}
// 都正确则返回数组长度 + 1
return len + 1;
}
private void swap(int[] nums, int index1, int index2) {
int temp = nums[index1];
nums[index1] = nums[index2];
nums[index2] = temp;
}
}
需要特别注意:这里赋值有先后顺序,写成 swap(nums, i, nums[i] - 1); 就会出错。
复杂度分析:
- 时间复杂度:\(O(N)\),这里 N 是数组的长度。
- 空间复杂度:\(O(1)\)。
说明:while 循环不会每一次都把数组里面的所有元素都看一遍。如果有一些元素在这一次的循环中被交换到了它们应该在的位置,那么在后续的遍历中,由于它们已经在正确的位置上了,代码再执行到它们的时候,就会被跳过。
最极端的一种情况是,在第 1 个位置经过这个 while 就把所有的元素都看了一遍,这个所有的元素都被放置在它们应该在的位置,那么 for 循环后面的部分的 while 的循环体都不会被执行。
平均下来,每个数只需要看一次就可以了,while 循环体被执行很多次的情况不会每次都发生。这样的复杂度分析的方法叫做均摊复杂度分析。
最后再遍历了一次数组,最坏情况下要把数组里的所有的数都看一遍,因此时间复杂度是 \(O(N)\)。
554. 砖墙
你的面前有一堵矩形的、由 n 行砖块组成的砖墙。这些砖块高度相同(也就是一个单位高)但是宽度不同。每一行砖块的宽度之和相等。
你现在要画一条 自顶向下 的、穿过 最少 砖块的垂线。如果你画的线只是从砖块的边缘经过,就不算穿过这块砖。你不能沿着墙的两个垂直边缘之一画线,这样显然是没有穿过一块砖的。
给你一个二维数组 wall ,该数组包含这堵墙的相关信息。其中,wall[i] 是一个代表从左至右每块砖的宽度的数组。你需要找出怎样画才能使这条线 穿过的砖块数量最少 ,并且返回 穿过的砖块数量 。
示例 1:

输入:wall = [[1,2,2,1],[3,1,2],[1,3,2],[2,4],[3,1,2],[1,3,1,1]]
输出:2
示例 2:
输入:wall = [[1],[1],[1]]
输出:3
答案
方法一:哈希表
思路及算法
由于砖墙是一面矩形,所以对于任意一条垂线,其穿过的砖块数量加上从边缘经过的砖块数量之和是一个定值,即砖墙的高度。
因此,问题可以转换成求「垂线穿过的砖块边缘数量的最大值」,用砖墙的高度减去该最大值即为答案。
虽然垂线在每行至多只能通过一个砖块边缘,但是每行的砖块边缘也各不相同,因此我们需要用哈希表统计所有符合要求的砖块边缘的数量。
注意到题目要求垂线不能通过砖墙的两个垂直边缘,所以砖墙两侧的边缘不应当被统计。因此,我们只需要统计每行砖块中除了最右侧的砖块以外的其他砖块的右边缘即可。
具体地,我们遍历砖墙的每一行,对于当前行,我们从左到右地扫描每一块砖,使用一个累加器记录当前砖的右侧边缘到砖墙的左边缘的距离,将除了最右侧的砖块以外的其他砖块的右边缘到砖墙的左边缘的距离加入到哈希表中。最后我们遍历该哈希表,找到出现次数最多的砖块边缘,这就是垂线经过的砖块边缘,而该垂线经过的砖块数量即为砖墙的高度减去该垂线经过的砖块边缘的数量。
其实就是求每块砖的前缀和,然后记录在哈希表(前缀和, 出现次数)中,找到出现次数最多的砖块边缘,这就是垂线经过的砖块边缘,而该垂线经过的砖块数量即为砖墙的高度减去该垂线经过的砖块边缘的数量。
代码
class Solution {
public int leastBricks(List<List<Integer>> wall) {
Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
for (List<Integer> widths : wall) {
int n = widths.size();
int sum = 0;
for (int i = 0; i < n - 1; i++) {
sum += widths.get(i);
cnt.put(sum, cnt.getOrDefault(sum, 0) + 1);
}
}
int maxCnt = 0;
for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
maxCnt = Math.max(maxCnt, entry.getValue());
}
return wall.size() - maxCnt;
}
}
复杂度分析
-
时间复杂度:\(O(nm)\),其中 n 是砖墙的高度,m 是每行砖墙的砖的平均数量。我们需要遍历每行砖块中除了最右侧的砖块以外的每一块砖,将其右侧边缘到砖墙的左边缘的距离加入到哈希表中。
-
空间复杂度:\(O(nm)\),其中 n 是砖墙的高度,m 是每行砖墙的砖的平均数量。我们需要将每行砖块中除了最右侧的砖块以外的每一块砖的右侧边缘到砖墙的左边缘的距离加入到哈希表中。
621. 任务调度器
给你一个用字符数组 tasks 表示的 CPU 需要执行的任务列表。其中每个字母表示一种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。在任何一个单位时间,CPU 可以完成一个任务,或者处于待命状态。
然而,两个 相同种类 的任务之间必须有长度为整数 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
你需要计算完成所有任务所需要的 最短时间 。
示例 1:
输入:tasks = ["A","A","A","B","B","B"], n = 2
输出:8
解释:A -> B -> (待命) -> A -> B -> (待命) -> A -> B
在本示例中,两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间,而执行一个任务只需要一个单位时间,所以中间出现了(待命)状态。
示例 2:
输入:tasks = ["A","A","A","B","B","B"], n = 0
输出:6
解释:在这种情况下,任何大小为 6 的排列都可以满足要求,因为 n = 0
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
诸如此类
示例 3:
输入:tasks = ["A","A","A","A","A","A","B","C","D","E","F","G"], n = 2
输出:16
解释:一种可能的解决方案是:
A -> B -> C -> A -> D -> E -> A -> F -> G -> A -> (待命) -> (待命) -> A -> (待命) -> (待命) -> A
哈希表记录出现次数
思路与算法
我们首先考虑所有任务种类中执行次数最多的那一种,记它为 A,的执行次数为 maxExec。
我们使用一个宽为 n+1 的矩阵可视化地展现执行 A 的时间点。其中任务以行优先的顺序执行,没有任务的格子对应 CPU 的待命状态。由于冷却时间为 n,因此我们将所有的 A 排布在矩阵的第一列,可以保证满足题目要求,并且容易看出这是可以使得总时间最小的排布方法,对应的总时间为:
同理,如果还有其它也需要执行 maxExec 次的任务,我们也需要将它们依次排布成列。例如,当还有任务 B 和 C 时,我们需要将它们排布在矩阵的第二、三列。
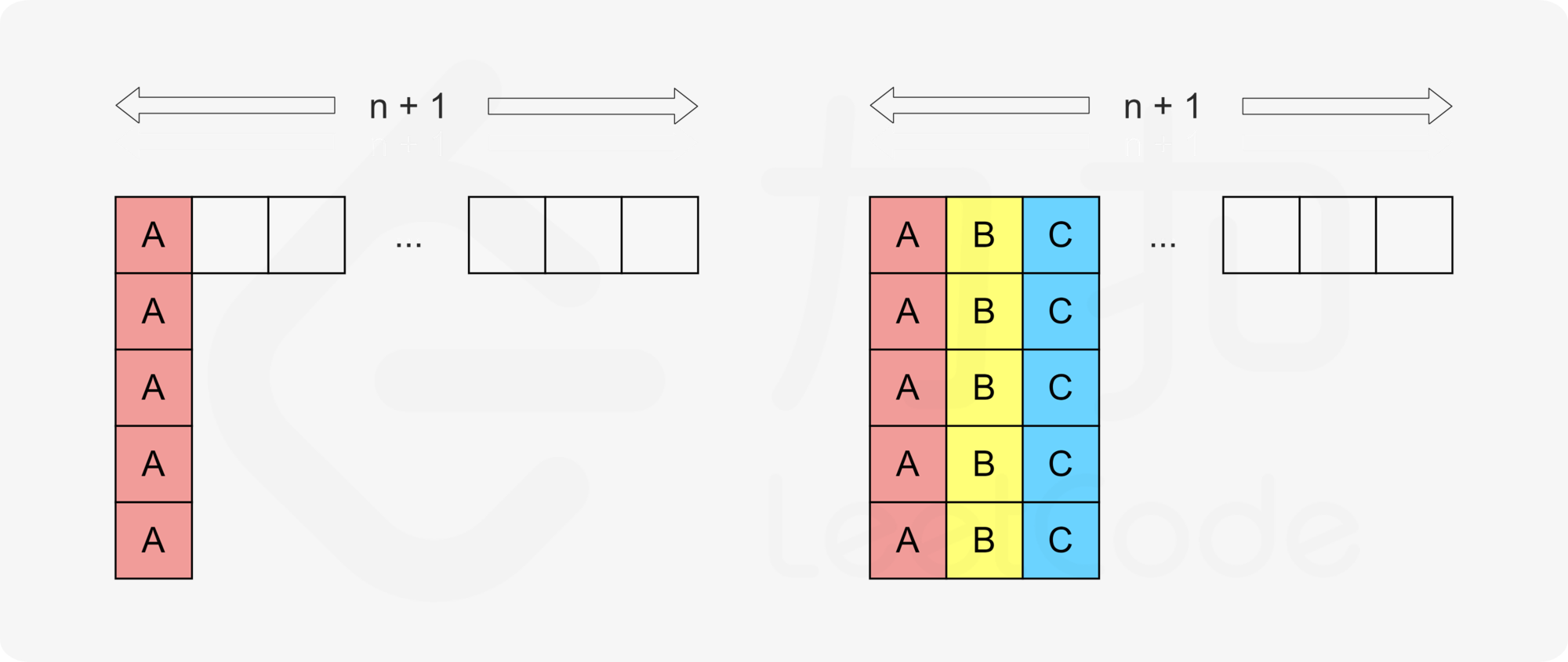
如果需要执行 maxExec 次的任务的数量为 maxCount,那么类似地可以得到对应的总时间为:
读者可能会对这个总时间产生疑问:如果 \(\textit{maxCount} > n+1\),那么多出的任务会无法排布进矩阵的某一列中,上面计算总时间的方法就不对了。我们把这个疑问放在这里,先「假设」一定有 \(\textit{maxCount} \leq n+1\)。
处理完执行次数为 maxExec 次的任务,剩余任务的执行次数一定都小于 maxExec,那么我们应当如何将它们放入矩阵中呢?一种构造的方法是,我们从倒数第二行开始,按照反向列优先的顺序(即先放入靠左侧的列,同一列中先放入下方的行),依次放入每一种任务,并且同一种任务需要连续地填入。例如还有任务 D,E 和 F 时,我们会按照下图的方式依次放入这些任务。
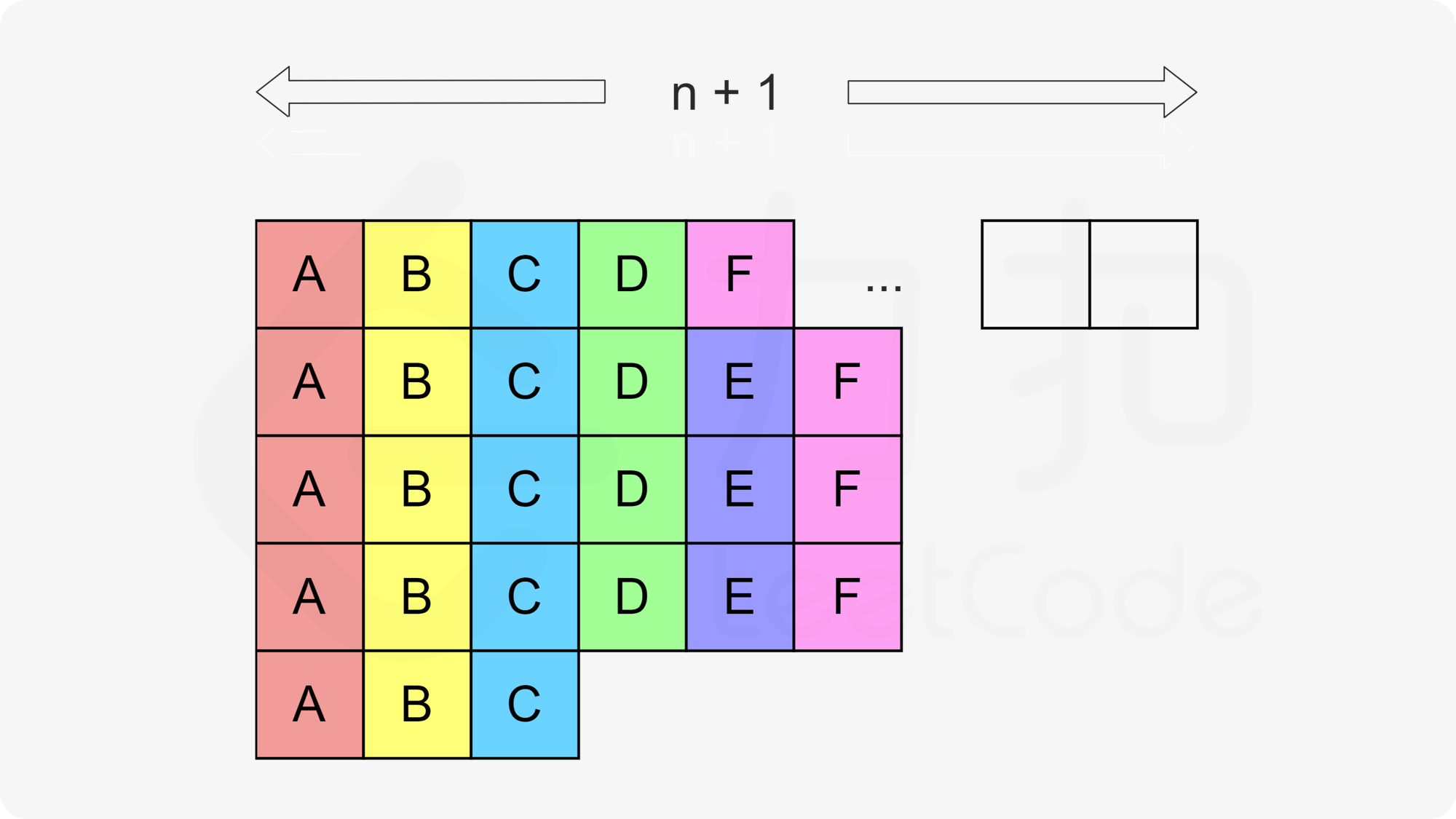
对于任意一种任务而言,一定不会被放入同一行两次(否则说明该任务的执行次数大于等于 maxExec),并且由于我们是按照列优先的顺序放入这些任务,因此任意两个相邻的任务之间要么间隔 n(例如上图中位于同一列的相同任务),要么间隔 n+1(例如上图中第一列和第二列的 F),都是满足题目要求的。因此如果我们按照这样的方法填入所有的任务,那么就可以保证总时间不变,仍然为:
当然,这些都建立在我们的「假设」之上,即我们不会填「超出」n+1 列。但读者可以想一想,如果我们真的填「超出」了 n+1 列,会发生什么呢?
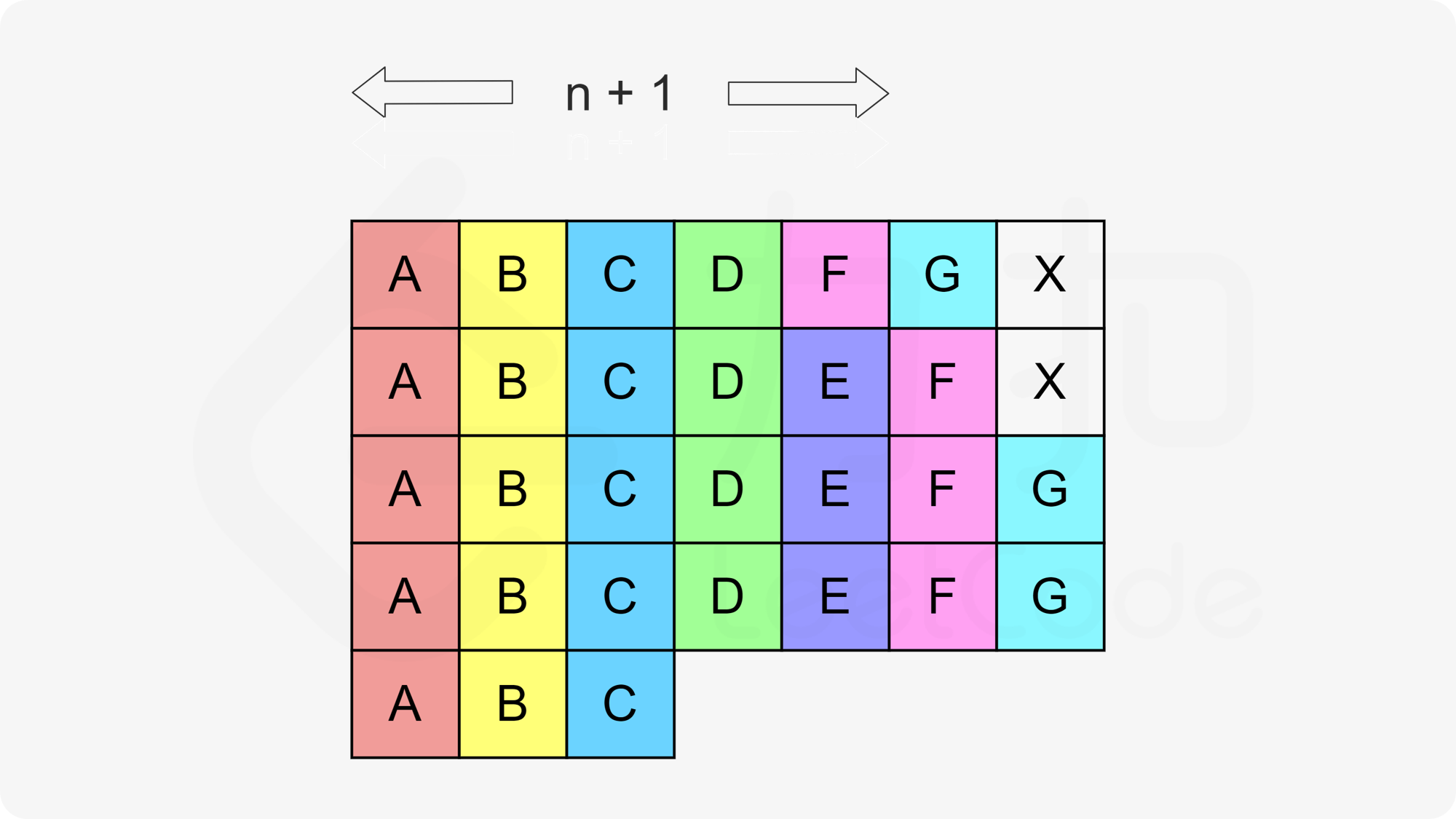
上图给出了一个例子,此时 n+1=5 但我们填了 7 列。标记为 X 的格子表示 CPU 的待命状态。看上去我们需要 (5−1)×7+4=32 的时间来执行所有任务,但实际上如果我们填「超出」了 n+1 列,那么所有的 CPU 待命状态都是可以省去的。这是因为 CPU 待命状态本身只是为了规定任意两个相邻任务的执行间隔至少为 n,但如果列数超过了 n+1,那么就算没有这些待命状态,任意两个相邻任务的执行间隔肯定也会至少为 n。此时,总执行时间就是任务的总数 \(∣task∣\)。
同时我们可以发现:
- 如果我们没有填「超出」了 n+1 列,那么图中存在 0 个或多个位置没有放入任务,由于位置数量为 \((\textit{maxExec} - 1)(n + 1) + \textit{maxCount}\),因此有:
- 如果我们填「超出」了 n+1 列,那么同理有:
因此,在任意的情况下,需要的最少时间就是 \((\textit{maxExec} - 1)(n + 1) + \textit{maxCount}\) 和 \(|\textit{task}|\) 中的较大值。
代码
class Solution {
public int leastInterval(char[] tasks, int n) {
Map<Character, Integer> freq = new HashMap<Character, Integer>();
// 最多的执行次数
int maxExec = 0;
for (char ch : tasks) {
int exec = freq.getOrDefault(ch, 0) + 1;
freq.put(ch, exec);
maxExec = Math.max(maxExec, exec);
}
// 具有最多执行次数的任务数量
int maxCount = 0;
for (Map.Entry<Character, Integer> entry : freq.entrySet()) {
int value = entry.getValue();
if (value == maxExec) {
++maxCount;
}
}
return Math.max((maxExec - 1) * (n + 1) + maxCount, tasks.length);
}
}
复杂度分析
-
时间复杂度:\(O(|\textit{task}| + |\Sigma|)\),其中 \(|\Sigma|\) 是数组 task 中出现任务的种类,在本题中任务用大写字母表示,因此 \(|\Sigma|\) 不会超过 26。
-
空间复杂度:\(O(|\Sigma|)\)。
笔者将不定期更新【考研或就业】的专业相关知识以及自身理解,希望大家能【关注】我。
如果觉得对您有用,请点击左下角的【点赞】按钮,给我一些鼓励,谢谢!
如果有更好的理解或建议,请在【评论】中写出,我会及时修改,谢谢啦!
本文来自博客园,作者:Nemo&
转载请注明原文链接:https://www.cnblogs.com/blknemo/p/14473441.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号