【算法】分治法四步走

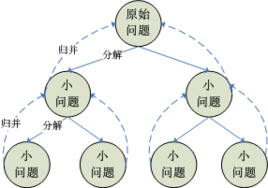
分治法在每一层递归上都有三个步骤：

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题
2. 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题
3. 合并：将各个子问题的解合并为原问题的解。

适用场景

适用于我们的问题是一个能被分解成多个小问题的大问题的时候

• 原问题 = 子类问题 + 当前问题
• 树：有关于树的问题都可以使用分治法，根左右
• 二分算法面对中间分叉，不能确定是往左走，还是往右走的时候，我们就可以使用分治算法，递归，给他左右都走一遍。

分治四步走

由于分治法一般采用递归方法实现，所以大家可以结合【算法】递归三步走来进行理解。

采取的数学思想为数学归纳法，由1递推到n。
数学归纳法是一种证明方法，而我们此处需要证明的是我们的算法函数（分治函数）可以解决我们的当前问题n，并由着这种证明的递推思路向下进行编程。

1. 明确分解策略

对应数学归纳法中需要被证明的原问题n。
我们需要证明我们的这个函数可以解决原问题n

1.明确分解策略：明确大问题通过怎样的分解策略一步步分解为最终的小问题，之后我们需要根据分解策略明确函数的功能。

特别注意：无论如何，明确函数功能都是我们最开始必须要做的事情！！！

一般情况下有两种分解策略：

• 前缀分解：函数需要有计数f(index)，来确定前缀分解范围\([0, index]\)。问题规模n = 问题规模n-1 + 当前问题
• 范围分解：函数就需要有范围域f(leftIndex, rightIndex)来确定分解范围\([leftIndex, rightIndex]\)；左子树 + 根 + 右子树

如果是前缀分解，那么我们的函数需要有计数(index)，来记录前缀分解的范围\([0, index]\)。

比如说，快速排序的大的问题可以分解为就是将n个元素摆到正确位置，汉诺塔的大的问题就是将n个圆盘由下而上摆到正确位置。

如果我们的分解策略如果是折半分解，那么我们的函数就需要有范围域(leftIndex, rightIndex)来确定分解范围\([leftIndex, rightIndex]\)；

注意：如果有多个分解域，我们就需要判断一下是不是每个域都要进行分解，每需要分解一次，就需要一个范围域(leftIndex, rightIndex)。
最简单的例子：树的先序遍历，分解策略：根左右（根节点、左子树、右子树）

2. 寻找最小问题（初始条件）

对应数学归纳法中的最小问题n=1。
我们需要证明我们的这个函数，当这个最小问题n=1的时候是成立的

2.寻找最小问题：最小问题也就是大问题的最简化版本，问题的起始状态，最小子问题即是出口。
（其他问题都是由最小问题初始条件递推过来的）

最简单的例子：树的先序遍历，最小问题：根节点为空，返回return

比如说，快速排序没有元素或者只有一个元素（leftIndex >= rightIndex）的时候。

3. 划分子类问题（未来）

对于数学归纳法中的子类问题n=k。
我们假设我们的函数n=k的时候是成立的，是可以解决子类问题的

子类问题：子类问题与原问题有相同的结构，是一样的，只不过规模小一些。\(原问题 ∽ 子类问题\)，如 （\(原树 ∽ 左右子树\)）
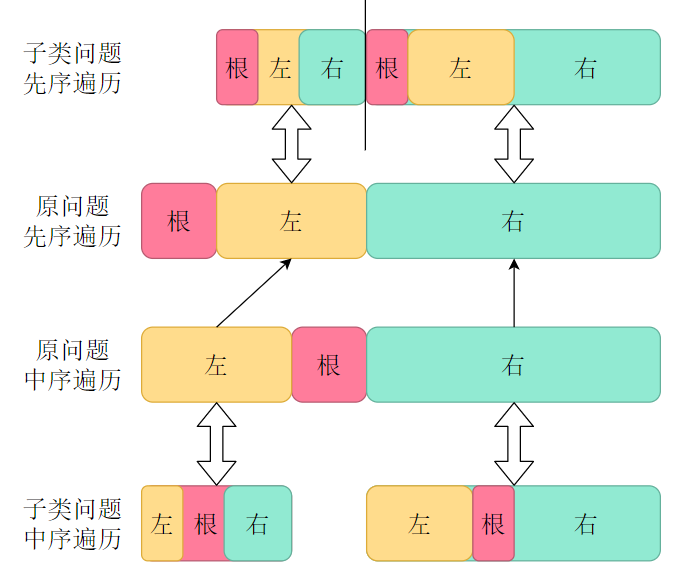
例子：比如树的中序遍历序列，按根节点划分之后，左右还是中序遍历序列。

类比：类似于数学里面的相似三角形。

3.划分子类问题：使用分解策略将大问题分解为 当前问题 + 子类问题（即 原问题 = 子类问题 + 当前问题，我们当前只能解决当前问题（现在），子类问题只起到划分的作用，属于未来，我们无法解决未来）。子类问题也就是介于最小问题与大问题之间的问题，与大问题有相同的结构，比大问题稍稍小那么一点，这使得子类问题具有解决大问题的通用性，即 可以通过子类问题找到大问题的通解。由子类问题得到解决方法。

特别注意：分治算法只去操作解决当前的问题，即 当前元素（如 根节点），对其他划分出来的子类问题（如 左右子树）均不操作解决，只起到划分的作用。

---

子类问题划分技巧：（找相似法）
由于原问题与子类问题相似，所以我们可以按照原问题提供的已知条件来寻找相似的子类问题所需要提供的条件。

例子：
问题：已知树的先序遍历、中序遍历，求出后序遍历。

• 原问题：提供大树的先序遍历序列，大树的中序遍历序列
• 子类问题：提供左右子树的中序遍历序列，根据左右子树数量来找出左右子树的先序遍历序列

你看看，上面的原问题与子类问题是不是一样的结构，相似！

---

最简单的例子：树的先序遍历，

• 当前问题：根，
• 子类问题：根左右（根节点、左子树、右子树），
• 访问根节点（因为只有当前节点根节点能够给我们操作，其他的左右子树都是起到划分的作用）

比如说，快速排序的当前问题就是将一个元素摆到正确位置，汉诺塔的当前问题就是将一个最下面的圆盘摆到正确位置。

4. 解决当前问题（现在）

对应数学归纳法中的当前问题n=k+1。
最后，通过我们的递推关系式推出函数在n=k+1的时候也成立，也可以解决问题。进而我们就可以知道当函数为n的时候，可以解决原问题。

4.解决当前问题：这个按照问题的逻辑进行处理，分治算法只去操作解决当前的问题，即 当前元素（如 根节点），对其他划分出来的子类问题（如 左右子树）均不操作解决，只起到划分的作用。

注意：在我们上一步划分子类问题之后，我们应该解决当前问题，但是这个当前问题的解决应该位于子类问题划分的之前、中间还是之后，这个就要具体题目具体分析了。
例如：

• 先序遍历：****当前问题（根）、子类问题（左子树）、子类问题（右子树）
• 中序遍历：子类问题（左子树）、当前问题（根）、子类问题（右子树）
• 后序遍历：子类问题（左子树）、子类问题（右子树）、当前问题（根）

在解决当前问题的时候，我们可能会需要结合之前划分子类问题的结果返回值（不一定），也可能不需要，作为单机问题去解决。

例如，我们在上一步中划分出了左右子树，这一步中我们可以将根节点与左右子树的根节点相连，形成一个完整的树。

折半分解

分治算法其实是二分算法的递归形式，他代表了并行执行，也就是说，如果我们的二分算法面对中间分叉，并不能确定是往左走，还是往右走，我们就可以使用分治算法，递归，左右都给他走一遍。

相当于二分算法是串行的一种迭代算法，而分治算法是一种并行的递归算法。

折半分解是我们在分治法中最常用的，所以这里提出来特别介绍。
此算法常用于递归操作树，划分树的左右子树。

1. 明确分解策略：折半分解，左右边界(leftIndex, rightIndex)，分解线midIndex = leftIndex + (rightIndex - leftIndex) / 2

2. 寻找最小问题：leftIndex > rightIndex或者leftIndex >= rightIndex

3. 划分子类问题：f(leftIndex, midIndex - 1)和f(midIndex + 1, rightIndex)

4. 解决当前问题：root.leftIndex = f(leftIndex, midIndex - 1)和root.rightIndex = f(midIndex + 1, rightIndex)

大家可以看看面试题 08.03. 魔术索引这道题，有序，如果使用二分算法，我们不能确定面对分叉是应该往左走，还是往右走，所以我们得使用分治算法，左右都走一遍。

四步走实例

1. 明确分解策略

第一步，明确怎么把大的问题一步步分解为最终的小问题；并明确这个函数的功能是什么，它要完成什么样的一件事。
分解策略：大问题 = n * 小问题。如果大问题是一个数组，那么小问题就是数组中的一个元素。
如果我们的分解策略如果是折半分解，那么我们的函数就需要有范围域(leftIndex, rightIndex)来确定分解范围；
如果是递减分解，那么我们的函数需要有计数(num)，来记录递减分解结果。

比如说，快速排序的大的问题可以分解为就是将n个元素摆到正确位置，汉诺塔的大的问题就是将n个圆盘由下而上摆到正确位置。

比如说，快速排序算法的大问题就是将数组中的n个元素进行排序摆放到正确的位置，那么分解而成的小问题就是将数组中的一个元素摆放到正确的位置。
而汉诺塔的大问题就是将A柱子上的n个盘子借用B柱子由大到小放在C柱子上，那么分解而成的小问题就是将A柱子上的最底下的最大盘子借用B放在C柱子上。

而这个功能，是完全由你自己来定义的。也就是说，我们先不管函数里面的代码是什么、怎么写，而首先要明白，你这个函数是要用来干什么的。

例如：面试题 04.02. 最小高度树
给定一个有序整数数组，元素各不相同且按升序排列，编写一个算法，创建一棵高度最小的二叉搜索树。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

          0 
         / \ 
       -3   9 
       /   / 
     -10  5 

要做出这个题，
第一步，要明确我们的分解策略，这里因为是二叉树，所以采用的方法一般是通过根节点划分左右子树，我的分解策略是折半分解；
既然分解策略是折半分解，那么我们即将要写出的这个函数必须指明分解范围，不然没有办法进行折半分解。

明确分解策略：
原问题=创建一棵高度最小的二叉搜索树，折半分解；
子类问题=通过根节点划分左右子树创建左右高度最小的左右子树；
当前问题=创建一个根左右3个节点的二叉树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode leftIndex;
 *     TreeNode rightIndex;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {

        return f(nums, 0, nums.length - 1);
    }

    // 分治法递归需要重新构造函数
	// 按(leftIndex, rightIndex)区域进行划分子树
	// 明确分解策略：大问题=创建一棵高度最小的二叉搜索树，折半分解，小问题=通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
    public TreeNode f(int[] nums, int leftIndex, int rightIndex) {
        
    }
}

2. 寻找最小问题（初始条件）

分治就是在函数实现的内部代码中，将大问题不断的分解为子类问题，再将小问题进一步分解为更小的问题。所以，我们必须要找出分治的结束条件，即 给定一个分解的阈值，不然的话，它会一直分解自己，无穷无尽。

必须有一个明确的结束条件。因为分治就是有“分”有“并”，所以必须又有一个明确的点，到了这个点，就不用“分解下去”，而是开始“合并”。

第二步，我们需要找出当参数为何值、分解到何种程度时，分治结束，之后直接把结果返回。
（一般为初始条件，然后从初始条件一步一步扩充到最终结果）

注意：这个时候我们必须能根据这个参数的值，能够直接知道函数的结果是什么。

让我们继续完善上面那个创建树。
第二步，寻找最小问题：
当leftIndex>rightIndex时，即 分解为空了，没有根节点，返回null；
那么递归出口就是leftIndex>rightIndex时函数返回null。

当leftIndex=rightIndex时，即 分解到只剩一个元素了，我们能够直接知道这最后一个元素就是根节点，返回最后一个元素；
leftIndex=rightIndex时函数返回new TreeNode(nums[leftIndex])（这种情况我们折半分解获取mid创建根节点的时候包含了，所以不写了）
并且这个不是最小的问题。

如下：

    // 分治法递归需要重新构造函数
	// 按(leftIndex, rightIndex)区域进行划分子树
	// 明确分解策略：大问题=创建一棵高度最小的二叉搜索树，折半分解，小问题=通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
    public TreeNode f(int[] nums, int leftIndex, int rightIndex) {
        if (leftIndex > rightIndex) {
            return null;
        }
    }

当然，当l=r时，我们也是知道f(r)等于多少的，f(r)也可以作为递归出口。分治出口可能并不唯一的。

3. 划分子类问题

特别注意：分治算法只去操作解决当前的问题，即 当前元素（如 根节点），对其他划分出来的子类问题（如 左右子树）均不操作解决，只起到划分的作用。

第三步，之前我们明确了分解策略，现在正是使用的时候了，我们需要使用这个分解策略，将大问题分解为子类问题。这样就能一步步分解到最小问题，然后作为函数出口。

• 最小问题：分解至空时，l>r，f(l)即为null
• 分解策略：折半分解，f(nums, l, r) → f(nums, l, (l+r)/2 - 1) , f(nums, (l+r)/2 + 1, r)
• 当前问题：根节点，mid
• 子类问题：左右子树数组，(leftIndex, midIndex-1)和(midIndex+1, rightIndex)。

分治：

• 分：将f(nums, l, r) → f(nums, l, (l+r)/2) , f(nums, (l+r)/2+1, r)了。这样，问题就由n缩小为了n/2，我们只需要找到这n/2个元素的最大值即可。就这样慢慢从f(n),f(n/2)“分”到f(1)。
• 并：这样就可以从1，一步一步“并”到n/2,n...

    // 分治法递归需要重新构造函数
	// 按(leftIndex, rightIndex)区域进行划分子树
	// 明确分解策略：大问题=创建一棵高度最小的二叉搜索树，折半分解，小问题=通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
    public TreeNode f(int[] nums, int leftIndex, int rightIndex) {
		// 寻找最小问题
        if (leftIndex > rightIndex) {
            return null;
        }
		
		// 划分子类问题：通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
		int midIndex = leftIndex + (rightIndex - leftIndex) / 2;
        TreeNode root = new TreeNode(nums[midIndex]);
		
        f(nums, leftIndex, midIndex - 1);
        f(nums, midIndex + 1, rightIndex);

        return root;
    }

4. 解决当前问题

第四步：解决当前问题。
上一步我们将大问题分解为了当前问题+子类问题，那么这个当前问题怎么解决呢，解决这个当前问题，也是为我们接下来的分解提供问题的解决方案，所以不能大意。
解决当前问题的方法，就是比较两个当前问题的大小，得出最大的一个值，问题即可解决。

特别注意：分治算法只去操作解决当前的当前问题（如 根节点），对其他划分出来的子类问题（如 左右子树）均不操作解决，只起到划分的作用。

这里的解决合并就是将子类问题合并为一个完整的大问题，方便我们求出大问题的答案，即 创建一个根左右3个节点的二叉树。

    // 分治法递归需要重新构造函数
	// 按(leftIndex, rightIndex)区域进行划分子树
	// 明确分解策略：大问题=创建一棵高度最小的二叉搜索树，折半分解，小问题=通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
    public TreeNode f(int[] nums, int leftIndex, int rightIndex) {
		// 寻找最小问题
        if (leftIndex > rightIndex) {
            return null;
        }
		
		// 划分子类问题：通过根节点划分左右子树，创建一个根左右3个节点的二叉树。
		int midIndex = leftIndex + (rightIndex - leftIndex) / 2;
        TreeNode root = new TreeNode(nums[midIndex]);
		
		// 解决当前问题：创建一个根左右3个节点的二叉树
        root.leftIndex = f(nums, leftIndex, midIndex - 1);
        root.rightIndex = f(nums, midIndex + 1, rightIndex);

        return root;
    }

---

到这里，分治四步走就完成了，那么这个分治函数的功能我们也就实现了。
可能初学的读者会感觉很奇妙，这就能得到最大值了？
那么，我们来一步一步推一下。

假设n为数组中元素的个数，f(n)则为函数
f(1)只有一个元素，可以得到一个确定的值
f(2)根据f(1)的值，也能确定了
f(4)根据f(2)的值，也能确定下来了
...
f(n/2)
f(n)根据f(n/2)也能确定下来了

你看看是不是解决了，n都能分治得到结果！

---

当前问题解决技巧

记录第一次满足条件的元素

初始化结果集：

res == null;

增加递归出口：

// 结果集：res
if (res != null) {
	return;
}

当前节点操作：只记录第一次res，只覆盖一次

// 结果集：res
if (条件 && res == null) {
	res = node;
	return;
}

记录最后一次满足条件的元素

当前节点操作：与记录第一次满足条件的元素的区别在于没有判断res == null，每次都会覆盖当前结果集，最后会得到最后一次满足条件的结果集

// 结果集：res
if (条件) {
	res = node;
}

记录当前问题节点的前驱节点

遍历完当前问题节点node后，使用pre记录当前节点，然后使用node去继续前进遍历。

dfs(node.leftIndex);

visit(node);
pre = node;	// 记录当前节点，下一步当前节点就会移到其他位置，所以pre会记录当前节点的前驱结点

dfs(node.rightIndex);	//node的下一次递归

返回每个递归节点的结果值

当解决当前问题需要用到每个递归节点的返回值时，每个递归节点的结果都返回，每个递归节点的结果状态都关注，而不是返回void像上面标志位一样只关注叶子节点的结果状态。

如返回值boolean，找到了结果之后我们的方法就返回true，只要有一个true那就代表找到了，所以我们返回使用逻辑或recur(a) || recur(b)；
当然，还有一种情况就是，不符合条件我们就返回false，只要有一个false就代表不符合了，所以我们返回使用逻辑与recur(a) && recur(b)。

boolean res = dfs(board, word, i + 1, j, k + 1)
           || dfs(board, word, i - 1, j, k + 1)
           || dfs(board, word, i, j + 1, k + 1)
           || dfs(board, word, i , j - 1, k + 1);
return res;

具体剪枝实例可以看下面的《剑指 Offer 12. 矩阵中的路径》

注意：这里可以看到，和我们上面明确函数功能所说的“返回数据”，即 返回数据应该是我们遇到递归出口之后，需要告诉给前一步递归的信息数据！对应上了。
我们需要把这一步找到了或者没找到的boolean信息传递给前一步递归，所以返回类型为boolean。

记忆化深搜

dfs，深度优先搜索，其实就是一种分治法，搜索当前节点 = 搜索当前节点的左子树 + 搜索当前节点的右子树。

由于只是深度优先搜索，而不是回溯法，只需要进行搜索，而不需要还原现场。

每个递归节点的结果都返回，每个递归节点的结果状态都关注，而不是返回void像上面标志位一样只关注叶子节点的结果状态。

每次递归前进都记录下当前的状态结果，剪掉之前记录过的枝叶，避免重复计算。

记忆化深搜，其实就是对递归dfs暴力的一种优化，将计算过的记录下来，避免重复计算。记忆化深搜也属于DP的一种！

类比：类似于redis的cache缓存，缓存下方法的参数和当前状态结果，分别作为缓存的key和value，下次可以直接取出使用。

如返回值boolean，找到了结果之后我们的方法就返回true，只要有一个true那就代表找到了，所以我们返回使用逻辑或recur(a) || recur(b)；
当然，还有一种情况就是，不符合条件我们就返回false，只要有一个false就代表不符合了，所以我们返回使用逻辑与recur(a) && recur(b)。

boolean res = dfs(board, word, i + 1, j, k + 1)
           || dfs(board, word, i - 1, j, k + 1)
           || dfs(board, word, i, j + 1, k + 1)
           || dfs(board, word, i , j - 1, k + 1);`
return res;

---

例如走迷宫，遇到陷阱花费时间为3，要求求出花费时间最短的最优值。
我们就可以在每次递归都记录下当前的状态结果，存在dp[][]数组中；如果当前递归路径递归到该节点所花费时间大于之前记录的状态结果，则剪枝，不必向下继续递归了。

斐波那契数列

给定一个 n，求 斐波那契数列的第 n 项的值，要求用递归实现。

递归

那么，我们只需要套用上面的递归函数，并且处理好递归出口，就能把它写成递归的形式，代码实现如下：

int f(int n) {
    if(n <= 1) {
        return 1;
    }
    return f(n-1) + f(n-2);
}

递归求解的过程如下：

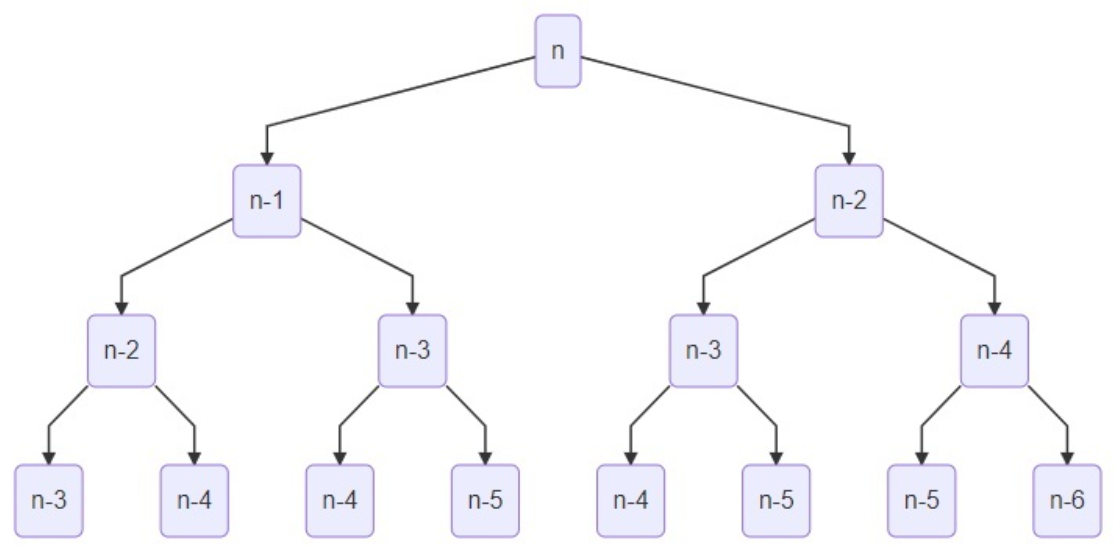
这是一棵二叉树，树的高度为 n，所以粗看递归访问时结点数为 \(2^n\)，但是仔细看，对于任何一棵子树而言，左子树的高度一定比右子树的高度大，所以不是一棵严格的完全二叉树。为了探究它实际的时间复杂度，我们改下代码：

int f(int n) {
    ++c[n]; // count记录每一层递归的次数
    if(n <= 1) {
        return 1;
    }
    return f(n-1) + f(n-2);
}

加了一句代码 ++c[n];，引入一个计数器，来看下在 n 为 16 的情况下，不同的 n 的 f(n) 这个函数的调用次数，如图所示：

n	c[n]
0	610
1	987
2	610
3	377
4	233
5	144
6	89
7	55
8	34
9	21
10	13
11	8
12	5
13	3
14	2
15	1
16	1

这是一个指数级的算法，随着 的不断增大，时间消耗呈指数级增长，我们在写代码的时候肯定是要避免这样的写法的，尤其是在服务器开发过程中，CPU 是一种极其宝贵的资源，任何的浪费都是可耻的。

记忆化搜索

递归求解斐波那契数列其实是一个深度优先搜索的过程，它是毫无优化的暴力枚举，对于 f(5) 的求解，我们发现，计算过程中其实有很多重叠子问题，例如 f(3) 被计算了 2 次，f(2) 被计算了 3 次，如图所示：

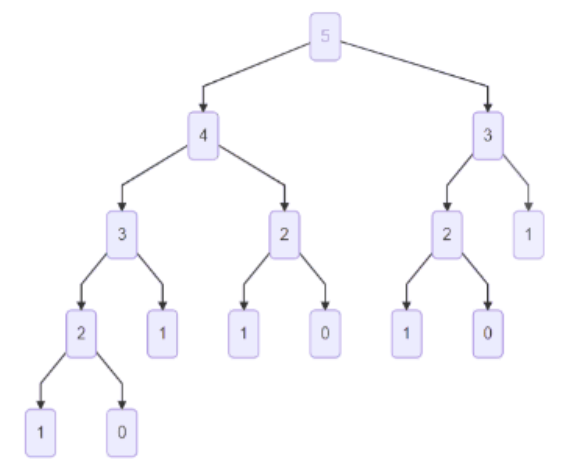
所以如果我们能够确保每个 f(i) 只被计算一次，问题就迎刃而解了。

可以考虑将 f(i) 计算出来的值存储到哈希数组 dp[i] 中，当第二次要访问 f(i) 时，直接取 dp[i] 的值即可，这样每次计算 f(i) 的时间复杂度变成了 \(O(1)\)，总共需要计算 f(2),f(3),...,f(n) ，总的时间复杂度就变成了 \(O(n)\) 。

这种用哈希数组来记录运算结果，避免重复运算的方法就是记忆化搜索。

public static int f(int n) {
    ++c[n];
	
	// 使用缓存记录
    if (dp[n] != 0) {
        return dp[n];
    }
	// 递归出口，也是最小问题
    if(n <= 1) {
        dp[0] = 1;
        dp[1] = 1;
        return 1;
    }
    dp[n] = f(n-1) + f(n-2);
    return dp[n];
}

来看下在 n 为 16 的情况下，不同的 n 的 f(n) 这个函数的调用次数，如图所示：

n	c[n]
0	1
1	2
2	2
3	2
4	2
5	2
6	2
7	2
8	2
9	2
10	2
11	2
12	2
13	2
14	2
15	1
16	1

可以看到算法由递归的指数级变为了多项式级，每个值只需计算一次即可，第二次访问无需重复计算，直接取出缓存即可。

https://zhuanlan.zhihu.com/p/438406757
https://blog.csdn.net/qq_54773252/article/details/122800467

多种分治法解法

面试题 04.06. 后继者

设计一个算法，找出二叉搜索树中指定节点的“下一个”节点（也即中序后继）。

如果指定节点没有对应的“下一个”节点，则返回null。

示例 1:

输入: root = [2,1,3], p = 1

  2
 / \
1   3

输出: 2

示例 2:

输入: root = [5,3,6,2,4,null,null,1], p = 6

      5
     / \
    3   6
   / \
  2   4
 /   
1

输出: null

按题意写函数功能

inorderSuccessor(root, p)方法就是在树root中找p节点的后继节点。

二叉搜索树，中序遍历，左根右

• 如果p大于等于根：后继节点在右边
• 如果p小于根：后继节点在左边或者在根

利用 BST 的特性，我们可以根据当前节点 root 与 p 的值大小关系来确定搜索方向：

• 若有 root.val <= p.val : 根据 BST 特性可知当前节点 root 及其左子树子节点均满足「值小于等于 p.val」，因此不可能是 p 点的后继，我们直接到 root 的右子树搜索 p 的后继（递归处理）；
• 若有 root.val > p.val : 当第一次搜索到满足此条件的节点时，在以 root 为根节点的子树中「位于最左下方」的值为 p 的后继，但也有可能 root 没有左子树，因此 p 的后继要么在 root 的左子树中（若有），要么是 root 本身，此时我们可以直接到 root 的左子树搜索，若搜索结果为空返回 root，否则返回搜索结果。

class Solution {

    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        if (root == null) {
            return null;
        }

        if (p.val >= root.val) {
            return inorderSuccessor(root.rightIndex, p);
        } else {
            TreeNode leftRet = inorderSuccessor(root.leftIndex, p);
            if (leftRet == null) {
                return root;
            } else {
                return leftRet;
            }
        }
    }
}

记录第一次满足条件的元素

如果找到p节点，那就置flag为true，中序遍历到后一个节点时设置结果res。

class Solution {
    boolean flag;	// 如果找到p节点，那就置为true，遍历到后一个节点时设置结果
    TreeNode res;

    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        dfs(root, p);
        return res;
    }

    public void dfs(TreeNode root, TreeNode p) {
        if (root == null) {
            return;
        }

        dfs(root.leftIndex, p);

        // 要求答案只改一次，不能被覆盖，就只要第一次成功的
        if (flag == true && res == null) {	// 不能放在最前面作为递归出口，因为需要中序遍历的后一个节点，此处是当前问题（当前节点）
            res = root;
            return;
        }
        if (root == p) {
            flag = true;
        }
		
        dfs(root.rightIndex, p);
    }
}

记录最后一次满足条件的元素

这个题目只要第一次满足条件，所以下面这种解法不成立，但是可以给大家一个样例看看。

class Solution {
    boolean flag;	// 如果找到p节点，那就置为true，遍历到后一个节点时设置结果
    TreeNode res;

    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        dfs(root, p);
        return res;
    }

    public void dfs(TreeNode root, TreeNode p) {
        if (root == null) {
            return;
        }

        dfs(root.leftIndex, p);
		
		// 区别在这里！！！！！！！！！！！！！！！！！！！！！！
        // 要求答案次次修改，能被覆盖，就只要最后一次成功的
        if (flag == true) {	// 不能放在最前面作为递归出口，因为需要中序遍历的后一个节点，此处是当前问题（当前节点）
            res = root;
            return;
        }
        if (root == p) {
            flag = true;
        }
		
        dfs(root.rightIndex, p);
    }
}

记录当前问题节点的前驱节点

我们使用pre节点来记录当前问题节点的前驱结点，每次遍历都需要前进（pre = root）。

class Solution {
    TreeNode res;
    TreeNode pre;

    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        dfs(root, p);
        return res;
    }

    public void dfs(TreeNode root, TreeNode p) {
        if (root == null || res != null) {
            return;
        }

        dfs(root.leftIndex, p);

        // 要求答案只改一次，不能被覆盖，就只要第一次成功的
        if (pre == p && res == null) {
            res = root;
            return;
        }
        pre = root;	// 前进
        dfs(root.rightIndex, p);
    }
}

这个故事告诉我们，前后只是相对概念，通过寻找前驱节点，也能解决后继节点的问题。

剑指 Offer 26. 树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。(约定空树不是任意一个树的子结构)

B是A的子结构， 即 A中有出现和B相同的结构和节点值。

例如:
给定的树 A:

     3
    / \
   4   5
  / \
 1   2

给定的树 B：

   4 
  /
 1

返回 true，因为 B 与 A 的一个子树拥有相同的结构和节点值。

示例 1：

输入：A = [1,2,3], B = [3,1]
输出：false

示例 2：

输入：A = [3,4,5,1,2], B = [4,1]
输出：true

我的

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

	// 是否是子结构
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if (A == null || B == null) return false;
		// 当前节点为根是否子结构，其他节点是否子结构
        return f(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

	// 是否从根节点开始就是子结构
    public boolean f(TreeNode A, TreeNode B) {
        if (B == null) return true;
        if (A == null) return false;
        // 原问题 = 当前问题 + 子类问题
		// 当前节点相等，左右子树都是子结构
        return A.val == B.val && f(A.left, B.left) && f(A.right, B.right);
    }
}

答案

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {

        if (A == null || B == null) {
            return false;
        }

        //先从根节点判断B是不是A的子结构，如果不是在分别从左右两个子树判断，
        //只要有一个为true，就说明B是A的子结构
        return recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }

    // 同步遍历，不相同就返回false
    public boolean recur(TreeNode A, TreeNode B) {
        //这里如果B为空，说明B已经访问完了，确定是A的子结构
        if (B == null)
            return true;

        //如果B不为空A为空，或者这两个节点值不同，说明B树不是
        //A的子结构，直接返回false
        if (A == null || A.val != B.val)
            return false;

        //当前节点比较完之后还要继续判断左右子节点
        return recur(A.left, B.left) && recur(A.right, B.right);

    }
}

疑似二分算法

面试题 08.03. 魔术索引

魔术索引。 在数组A[0...n-1]中，有所谓的魔术索引，满足条件A[i] = i。给定一个有序整数数组，编写一种方法找出魔术索引，若有的话，在数组A中找出一个魔术索引，如果没有，则返回-1。若有多个魔术索引，返回索引值最小的一个。

示例1:

 输入：nums = [0, 2, 3, 4, 5]
 输出：0
 说明: 0下标的元素为0

示例2:

 输入：nums = [1, 1, 1]
 输出：1

答案

这题我一看，有序，二分查找！结果根本就没办法确定是往左走还是往右走，直接给我没辙了。

就试了试分治算法，递归的二分算法，问题迎刃而解。

// 很遗憾，二分查找并不行，因为无论找到了什么满足条件的元素，其左右都可能出现满足条件的元素
// 只能分治算法
class Solution {
    public int findMagicIndex(int[] nums) {

        return f(nums, 0, nums.length - 1);
    }

    public int f(int[] nums, int leftIndex, int rightIndex) {
        if (leftIndex > rightIndex) {
            return -1;
        }

        int midIndex = leftIndex + (rightIndex - leftIndex) / 2;

        // 左边
        int leftAns = f(nums, leftIndex, midIndex - 1);

        // 中间
        if (leftAns != -1) {
            return leftAns;
        } else if (midIndex == nums[midIndex]) {
            return midIndex;
        }

        // 右边
        return f(nums, midIndex + 1, rightIndex);
    }
}

面试题 10.05. 稀疏数组搜索

稀疏数组搜索。有个排好序的字符串数组，其中散布着一些空字符串，编写一种方法，找出给定字符串的位置。

示例1:

 输入: words = ["at", "", "", "", "ball", "", "", "car", "", "","dad", "", ""], s = "ta"
 输出：-1
 说明: 不存在返回-1。

示例2:

 输入：words = ["at", "", "", "", "ball", "", "", "car", "", "","dad", "", ""], s = "ball"
 输出：4

答案

很明显，虽然有序，但是无法判断中间分叉该向左走还是向右走，所以采用分治算法。

class Solution {
    public int findString(String[] words, String s) {
        // 有序，二分，可是无法判断中间分叉该左走还是右走
        // 分治，递归
        return f(words, s, 0, words.length - 1);
    }

    public int f(String[] words, String s, int leftIndex, int rightIndex) {
        if (leftIndex > rightIndex) {
            return -1;
        }

        int midIndex = leftIndex + (rightIndex - leftIndex) / 2;

        if (s.equals(words[midIndex])) {
            return midIndex;
        }

        int leftAns = f(words, s, leftIndex, midIndex - 1);
        if (leftAns != -1) {
            return leftAns;
        }

        int rightAns = f(words, s, midIndex + 1, rightIndex);
        if (rightAns != -1) {
            return rightAns;
        }

        return -1;
    }
}

实例

最大数

在一个数组中找最大的数字。

分解策略：对半分

从l到r中找到最大的一个元素。

// 明确分解策略：大问题=从n个元素中找到最大的数字并返回，折半分解，小问题=从2个元素比较大小找到最大数字并返回。
int f(int[] nums, int l, int r) {

      // 寻找最小问题：最小问题即是只有一个元素的时候
      if (l >= r) {
            return nums[l];
      }

      // 使用分解策略
      int lMax = f(nums, l, (l+r)/2);
      int rMax = f(nums, (l+r)/2+1, r);

      // 解决次小问题：比较两个元素得到最大的数字

      return lMax > rMax ? lMax : rMax;
}

汉诺塔

汉诺塔的传说

汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

假如每秒钟一次，共需多长时间呢？移完这些金片需要 5845. 54 亿年以上，太阳系的预期寿命据说也就是数百亿年。真的过了 5845. 54 亿年，地球上的一切生命，连同梵塔、庙宇等，都早已经灰飞烟灭。

汉诺塔游戏的演示和思路分析:

1 ) 如果是有一个盘，A->C

如果我们有 n>= 2 情况，我们总是可以看做是两个盘 1 .最下边的盘 2. 上面的盘
2 ) 先把 最上面的盘A->B
3 ) 把最下边的盘A->C
4 ) 把B塔的所有盘 从 B->C

汉诺塔游戏的代码实现:

看老师代码演示:

package com.atguigu.dac;

public class Hanoitower {

	public static void main(String[] args) {
		hanoiTower(10, 'A', 'B', 'C');
	}
	
	//汉诺塔的移动的方法
	//使用分治算法
	// 明确分解策略：我们的问题是有n个盘子，可是如果是n个盘子的话我们不会分，不知道结果；如果盘子数量为1、2、3就好了，所以我们按盘子数依次减一分解
	public static void hanoiTower(int num, char a, char b, char c) {
		// 寻找最小问题：只有一个盘
		//如果只有一个盘
		if(num == 1) {
			System.out.println("第1个盘从 " + a + "->" + c);
		} else {
			// 解决次小问题：由于我们是按盘子数-1来进行分解的，所以次小问题是一个盘子和n-1个盘子的汉诺塔，将一个最下面的盘子摆放到正确的位置
			//如果我们有 n >= 2 情况，我们总是可以看做是两个盘 1.最下边的一个盘 2. 上面的所有盘
			//1. 先把 最上面的所有盘 A->B， 移动过程会使用到 c
			hanoiTower(num - 1, a, c, b);
			//2. 把最下边的盘 A->C
			System.out.println("第" + num + "个盘从 " + a + "->" + c);
			//3. 把B塔的所有盘 从 B->C , 移动过程使用到 a塔  
			hanoiTower(num - 1, b, a, c);
		}
	}
}

面试题 08.06. 汉诺塔问题

在经典汉诺塔问题中，有 3 根柱子及 N 个不同大小的穿孔圆盘，盘子可以滑入任意一根柱子。一开始，所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。

请编写程序，用栈将所有盘子从第一根柱子移到最后一根柱子。

你需要原地修改栈。

示例1:

 输入：A = [2, 1, 0], B = [], C = []
 输出：C = [2, 1, 0]

示例2:

 输入：A = [1, 0], B = [], C = []
 输出：C = [1, 0]

答案

• 当前问题：把最底下的第n块移过去
• 子类问题：把n-1块移过去

class Solution {
    /**
     * 将 A 上的所有盘子，借助 B，移动到C 上
     * @param A 原柱子
     * @param B 辅助柱子
     * @param C 目标柱子
     */
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        movePlate(A.size(), A, B, C);
    }

    private void movePlate(int num, List<Integer> A, List<Integer> B, List<Integer> C) {
        if (num == 1) {    // 只剩一个盘子时，直接移动即可
            C.add(A.remove(A.size() - 1));
            return;
        }

        movePlate(num - 1, A, C, B);   // 将 size-1 个盘子，从 A 移动到 B
        movePlate(1, A, B, C);
        // C.add(A.remove(A.size() - 1));   // 将 第size个盘子，从 A 移动到 C
        movePlate(num - 1, B, A, C);   // 将 size-1 个盘子，从 B 移动到 C
    }
}

206. 反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

输入：head = [1,2,3,4,5]
输出：[5,4,3,2,1]

示例 2：

输入：head = [1,2]
输出：[2,1]

示例 3：

输入：head = []
输出：[]

分治法

当然，头插法也可以做，但是这里为了体验分治法，我们使用分治法

• 分解策略：递减分解
• 函数功能：反转链表
• 最小问题：头节点为null，结果为null；只有一个节点时候，结果为头节点
• 划分子类问题：反转head.next的链表
• 解决当前问题：head.next.next = head。

  1 -> (2 <- 3 <- 4 <- ... <- n)

class Solution {
    public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }
        ListNode newHead = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return newHead;
    }
}

复杂度分析

• 时间复杂度：\(O(n)\)，其中 n 是链表的长度。需要对链表的每个节点进行反转操作。
• 空间复杂度：\(O(n)\)，其中 n 是链表的长度。空间复杂度主要取决于递归调用的栈空间，最多为 n 层。

912. 排序数组

给你一个整数数组 nums，请你将该数组升序排列。

示例 1：

输入：nums = [5,2,3,1]
输出：[1,2,3,5]

示例 2：

输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]

快速排序

class Solution {
    public int[] sortArray(int[] nums) {

        if (nums == null) {
            return null;
        }

        QuickSort(nums, 0, nums.length - 1);
        return nums;
    }

    public void QuickSort(int A[], int low, int high) {
        if(low >= high) {   //不能划分了，递归出口
            return;
        }
        int pivotpos = Partition(A, low, high);     //划分
        QuickSort(A, low, pivotpos-1);      //依次对两个子表进行递归排序划分
        QuickSort(A, pivotpos+1, high);
    }

    // 划分算法（一趟排序过程）
    public int Partition(int[] nums, int leftIndex, int rightIndex) {

        int temp = nums[leftIndex];

        while (leftIndex < rightIndex) {
            while (leftIndex < rightIndex && nums[rightIndex] >= temp) rightIndex--;
            nums[leftIndex] = nums[rightIndex];

            while (leftIndex < rightIndex && nums[leftIndex] <= temp) leftIndex++;
            nums[rightIndex] = nums[leftIndex];
        }

        nums[leftIndex] = temp;
        return leftIndex;
    }
}

面试题 04.02. 最小高度树

给定一个有序整数数组，元素各不相同且按升序排列，编写一个算法，创建一棵高度最小的二叉搜索树。

示例:

给定有序数组: [-10,-3,0,5,9],

一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

          0 
         / \ 
       -3   9 
       /   / 
     -10  5 

答案

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode leftIndex;
 *     TreeNode rightIndex;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {

        return f(nums, 0, nums.length - 1);
    }

    // 二分法需要重新构造函数
    public TreeNode f(int[] nums, int leftIndex, int rightIndex) {
        if (leftIndex > rightIndex) {
            return null;
        }
        int midIndex = leftIndex + (rightIndex - leftIndex) / 2;
        TreeNode root = new TreeNode(nums[midIndex]);
        root.leftIndex = f(nums, leftIndex, midIndex - 1);
        root.rightIndex = f(nums, midIndex + 1, rightIndex);

        return root;
    }

}

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

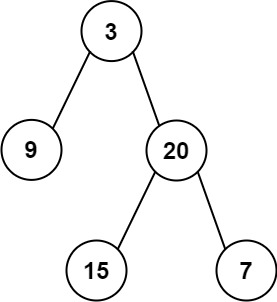
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

我的

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode leftIndex;
 *     TreeNode rightIndex;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode leftIndex, TreeNode rightIndex) {
 *         this.val = val;
 *         this.leftIndex = leftIndex;
 *         this.rightIndex = rightIndex;
 *     }
 * }
 */
class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {

        return f(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
    }

	// 分治法
    public TreeNode f(int[] preorder, int left1, int right1, int[] inorder, int left2, int right2) {
        if (left1 > right1 || left2 > right2) {
            return null;
        }

        int root = preorder[left1];
        int i = 0;
        for (i = 0; i < inorder.length; i++) {
            if (preorder[left1] == inorder[i]) {
                break;
            }
        }
        int leftLength = i - left2, rightLength = right2 - i;

        TreeNode leftIndex = f(preorder, left1 + 1, left1 + leftLength, inorder, left2, i - 1);
        TreeNode rightIndex = f(preorder, right1 - rightLength + 1, right1, inorder, i + 1, right2);
        return new TreeNode(preorder[left1], leftIndex, rightIndex);
    }
}

通过先序和中序数组生成后序数组

给出一棵二叉树的先序和中序数组，通过这两个数组直接生成正确的后序数组。

示例1
输入

[1,2,3],[2,1,3]

输出

[2,3,1]

我的

• 先序遍历边界：left1, right1
• 中序遍历边界：left2, right2
• 后序遍历边界：left0, right0

public class Solution {
    /**
     *
     * @param preOrder int整型一维数组 the array1
     * @param inOrder int整型一维数组 the array2
     * @return int整型一维数组
     */
    public static int[] postOrder;
    public static int[] findOrder (int[] preOrder, int[] inOrder) {
        // write code here
        // 先序：根左右
        // 中序：左根右
        // 后序：左右根
        postOrder = new int[preOrder.length];
        f(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1, 0, preOrder.length - 1);
        return postOrder;
    }
    // 从先序里面找到第一个元素，就是根节点，
    // 然后带着根节点去中序里面划分出左右子树的个数
    // 再带着左右子树的个数去划分先序数组
    // 函数功能：从先序找出第一个root，划分中序的左右
    // root仅与先序遍历中的根节点索引有关
    // left和right仅与中序遍历中的左右指针划分有关
    public static void f(int[] preOrder, int left1, int right1, int[] inOrder, int left2, int right2, int left0, int right0) {
        if (left1 > right1 || left2 > right2) {
            return;
        }

        // 在中序中找到根节点位置i
        int i = 0;
        for (i = left2; i < right2 && inOrder[i] != preOrder[left1]; i++);

        int leftLength = i - left2;
        int rightLength = right2 - i;

        // 左
        f(preOrder, left1 + 1, left1 + leftLength, inOrder, left2, i - 1, left0, left0 + leftLength - 1);
        // 右
        f(preOrder, right2 - rightLength + 1, right2, inOrder, i + 1, right2, right0 - rightLength,right0 - 1);
        // 根，后序遍历边界的右边界即是根
        postOrder[right0] = preOrder[left1];
    }
}

答案

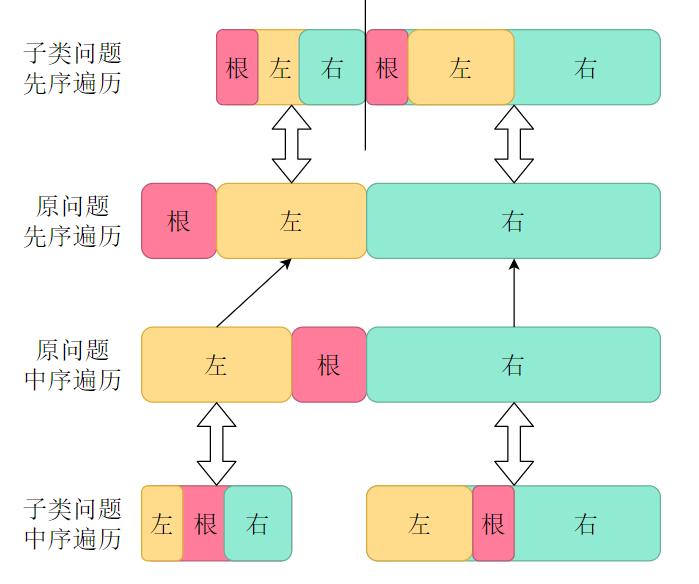
常规做法：先序遍历划分，中序遍历划分，public void f(int[] preOrder, int left1, int right1, int[] inOrder, int left2, int right2) {

1. 先序遍历的第一个元素作为根节点
2. 然后拿着根节点去中序遍历寻找可以得知其左右子树分别的数量
3. 拿着这个数量，我们就可以再去先序遍历里面进行划分左右子树
4. 这样就能递归得到后序遍历（左右根）了

import java.util.*;

public class Solution {
    /**
     * 
     * @param preOrder int整型一维数组 the array1
     * @param inOrder int整型一维数组 the array2
     * @return int整型一维数组
     */
    public int[] postOrder;
    public int num;
    public int[] findOrder (int[] preOrder, int[] inOrder) {
        // write code here
        // 先序：根左右
        // 中序：左根右
        // 后序：左右根
        postOrder = new int[preOrder.length];
        f(preOrder, 0, preOrder.length - 1, inOrder, 0, preOrder.length - 1);
        return postOrder;
    }
    // 从先序里面找到第一个元素，就是根节点，
    // 然后带着根节点去中序里面划分出左右子树的个数
    // 再带着左右子树的个数去划分先序数组
    // 函数功能：从先序找出第一个root，划分中序的左右
	// root仅与先序遍历中的根节点索引有关
	// left和right仅与中序遍历中的左右指针划分有关
    public void f(int[] preOrder, int left1, int right1, int[] inOrder, int left2, int right2) {
        if (left1 > right1 || left2 > right2) {
            return;
        }
        
        // 在中序中找到根节点位置i
        int i = 0;
        for (i = left2; i < right2 && inOrder[i] != preOrder[left1]; i++);
		
		int leftLength = i - left2;
		int rightLength = right2 - i;

        // 左
        f(preOrder, left1 + 1, left1 + leftLength, inOrder, left2, i - 1);
        // 右
        f(preOrder, right2 - rightLength + 1, right2, inOrder, i + 1, right2);
        // 根
        postOrder[num++] = preOrder[left1];
    }
}

答案二

简化做法：先序遍历找根，中序遍历划分，public void f(int[] preOrder, int root, int[] inOrder, int leftIndex, int rightIndex) {

1. 在先序遍历中找出根节点
2. 在中序遍历中进行左右划分
3. 在中序遍历中划分后，利用划分的左右子树数量，重新在先序遍历中找到根节点。

原问题 = 当前问题 + 子类问题

• 当前问题：找到根节点进行划分，然后按后序遍历（左右根）去存储
• 子类问题：依据根节点将中序遍历划分为左右子树中序遍历，用左右子树数量去先序遍历中找到左右子树根节点。（即 组成了与原问题相同结构的子类问题，左右子树中序遍历+左右子树先序遍历根节点）

import java.util.*;

public class Solution {
    /**
     * 
     * @param preOrder int整型一维数组 the array1
     * @param inOrder int整型一维数组 the array2
     * @return int整型一维数组
     */
    public int[] postOrder;
    public int num;
    public int[] findOrder (int[] preOrder, int[] inOrder) {
        // write code here
        // 先序：根左右
        // 中序：左根右
        // 后序：左右根
        postOrder = new int[preOrder.length];
        f(preOrder, 0, inOrder, 0, preOrder.length - 1);
        return postOrder;
    }
    // 从先序里面找到第一个元素，就是根节点，
    // 然后带着根节点去中序里面划分出左右子树的个数
    // 再带着左右子树的个数去划分先序数组
    // 函数功能：从先序找出第一个root，划分中序的左右
	// root仅与先序遍历中的根节点索引有关
	// left和right仅与中序遍历中的左右指针划分有关
    public void f(int[] preOrder, int root, int[] inOrder, int leftIndex, int rightIndex) {
        if (leftIndex > rightIndex) {
            return;
        }
        
        // 在中序中找到根节点位置i
        int i = 0;
        for (i = leftIndex; i < rightIndex && inOrder[i] != preOrder[root]; i++);
        // 左
        f(preOrder, root + 1, inOrder, leftIndex, i - 1);
        // 右
        f(preOrder, root + i - leftIndex + 1, inOrder, i + 1, rightIndex);
        // 根
        postOrder[num++] = preOrder[root];
    }
}

面试题 17.12. BiNode

二叉树数据结构TreeNode可用来表示单向链表（其中left置空，right为下一个链表节点）。实现一个方法，把二叉搜索树转换为单向链表，要求依然符合二叉搜索树的性质，转换操作应是原址的，也就是在原始的二叉搜索树上直接修改。

返回转换后的单向链表的头节点。

注意：本题相对原题稍作改动

示例：

输入： [4,2,5,1,3,null,6,0]
输出： [0,null,1,null,2,null,3,null,4,null,5,null,6]

只能操作当前元素

下面一定要注意了，只能操作当前元素，左右子树只起到划分的作用。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode leftIndex;
 *     TreeNode rightIndex;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {

    TreeNode pre;   // 链表的上一个元素

    // 二叉搜索树中序遍历有序
    public TreeNode convertBiNode(TreeNode root) {

        TreeNode head = new TreeNode(0);    // 单链表的伪头节点
        pre = head;
        f(root);
        return head.rightIndex;
    }

    // 二叉搜索树中序遍历有序
    public void f(TreeNode root) {

        if (root == null) {
            return;
        }

        // 划分左子树
        f(root.leftIndex);

        // 只能操作当前元素，让pre、root构成一条向右延伸的单链表
        pre.rightIndex = root;
        root.leftIndex = null;
        pre = root;
        
        // 划分右子树
        f(root.rightIndex);
    }
}

剑指 Offer 40. 最小的k个数

最小的k个数：输入整数数组 arr ，找出其中最小的 k 个数。例如，输入4、5、1、6、2、7、3、8这8个数字，则最小的4个数字是1、2、3、4。

示例 1：
输入：arr = [3,2,1], k = 2
输出：[1,2] 或者 [2,1]

示例 2：
输入：arr = [0,1,2,1], k = 1
输出：[0]

限制：
0 <= k <= arr.length <= 10000
0 <= arr[i] <= 10000

我的

快速排序

class Solution {

    boolean flag = false;
    int[] res;
    int k;

    public int[] getLeastNumbers(int[] arr, int k) {
        if (arr == null || k <= 0) {
            return new int[0];
        }
        // 这里需要注意，是k个数，第1个数是下标为0，所以要-1
        this.k = k - 1;

        quickSearch(arr, 0, arr.length - 1);
        return res;
    }

    public int partition(int[] arr, int leftIndex, int rightIndex) {

        int temp = arr[leftIndex];
        while (leftIndex < rightIndex) {
            while (leftIndex < rightIndex && arr[rightIndex] >= temp) rightIndex--;
            arr[leftIndex] = arr[rightIndex];

            while (leftIndex < rightIndex && arr[leftIndex] <= temp) leftIndex++;
            arr[rightIndex] = arr[leftIndex];
        }

        arr[leftIndex] = temp;
        return leftIndex;
    }

    public void quickSearch(int[] arr, int leftIndex, int rightIndex) {
        
        if (flag) {
            return;
        }

        int midIndex = partition(arr, leftIndex, rightIndex);

        if (midIndex == k) {
            flag = true;
            res = Arrays.copyOfRange(arr, 0, midIndex + 1);
            return;
        } else if (midIndex < k) {
            quickSearch(arr, midIndex + 1, rightIndex);
        } else {
            quickSearch(arr, leftIndex, midIndex - 1);
        }
    }
}

堆和大小顶堆

这道题出自《剑指offer》，是一道非常高频的题目。可以通过排序等多种方法求解。但是这里，我们使用较为经典的大顶堆（大根堆）解法进行求解。因为我知道有很多人可能一脸懵逼，所以，我们先复习一下大顶堆。

首先复习一下堆，堆(Heap)是计算机科学中一类特殊的数据结构的统称，我们通常是指一个可以被看做一棵完全二叉树的数组对象。

堆的特性是父节点的值总是比其两个子节点的值大或小。如果父节点比它的两个子节点的值都要大，我们叫做大顶堆。如果父节点比它的两个子节点的值都要小，我们叫做小顶堆。

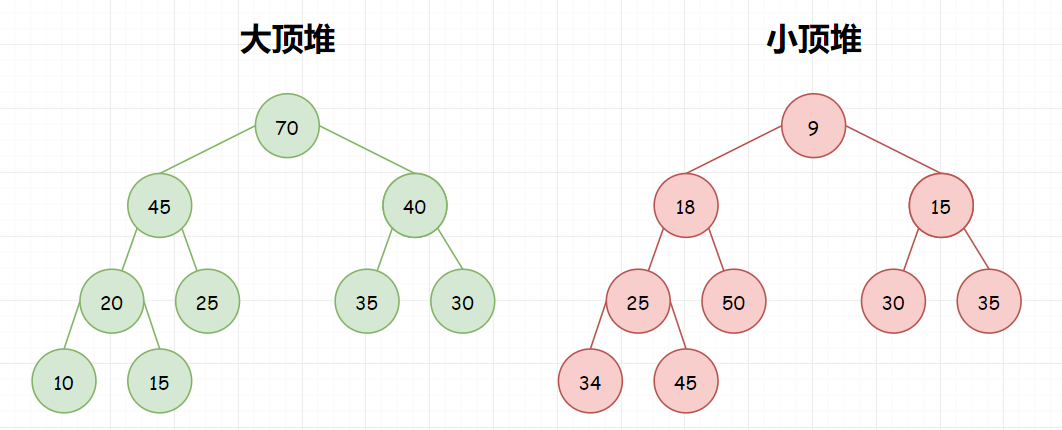
我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子。

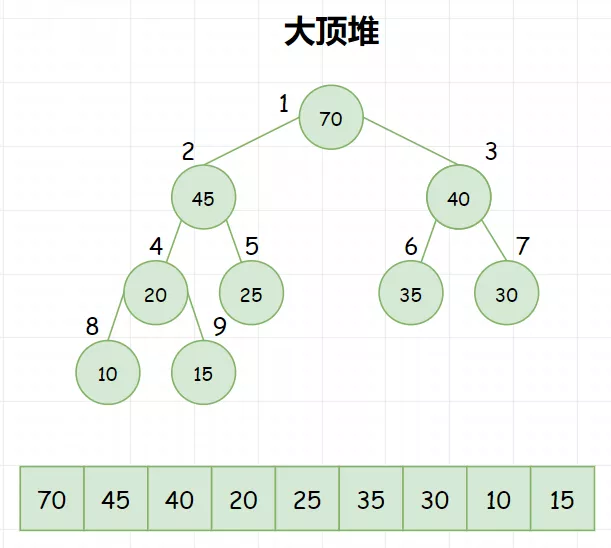
大顶堆，满足以下公式

\[arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2] \]

小顶堆也一样：

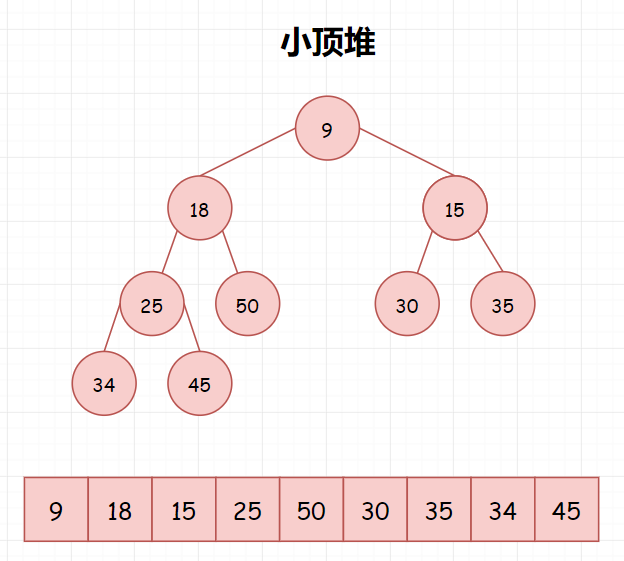
小顶堆，满足以下公式

\[arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2] \]

答案

上面我们学习了大顶堆，现在考虑如何用大根堆进行求解。

首先，我们创建一个大小为k的大顶堆。假如数组为[4,5,1,6,2,7,3,8]，k=4。大概是下面这样：

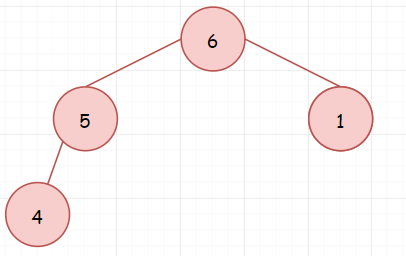
我想肯定这里有不知道如何建堆的同学。记住：对于一个没有维护过的堆（完全二叉树），我们可以从其最后一个节点的父节点开始进行调整。这个不需要死记硬背，其实就是一个层层调节的过程。

（从最后一个节点的父节点调整）

（继续向上调整）

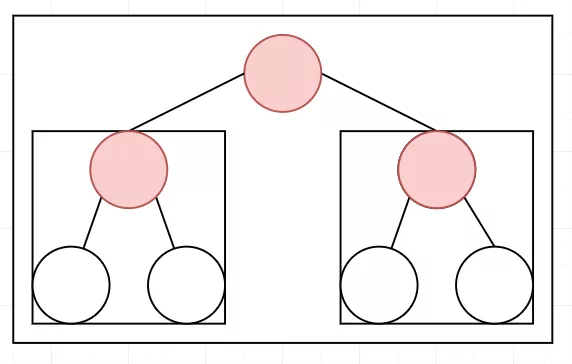
（继续向上调整）

建堆+调整的代码大概就是这样：（翻Java牌子）

   //建堆。对于一个还没维护过的堆，从他的最后一个节点的父节点开始进行调整。
    private void buildHeap(int[] nums) {
        //最后一个节点
        int lastNode = nums.length - 1;
        //记住：父节点 = (i - 1) / 2  左节点 = 2 * i + 1  右节点 = 2 * i + 2;
        //最后一个节点的父节点
        int startHeapify = (lastNode - 1) / 2;
        while (startHeapify >= 0) {
            //不断调整建堆的过程
            heapify(nums, startHeapify--);
        }
    }

    //调整大顶堆的过程
    private void heapify(int[] nums, int i) {
        //和当前节点的左右节点比较，如果节点中有更大的数，那么交换，并继续对交换后的节点进行维护
        int len = nums.length;
        if (i >= len)
            return;
        //左右子节点
        int c1 = ((i << 1) + 1), c2 = ((i << 1) + 2);
        //假定当前节点最大
        int max = i;
        //如果左子节点比较大，更新max = c1;
        if (c1 < len && nums[c1] > nums[max]) max = c1;
        //如果右子节点比较大，更新max = c2;
        if (c2 < len && nums[c2] > nums[max]) max = c2;
        //如果最大的数不是节点i的话，那么heapify(nums, max)，即调整节点i的子树。
        if (max != i) {
            swap(nums, max, i);
            //递归处理
            heapify(nums, max);
        }
    }

    private void swap(int[] nums, int i, int j) {
        nums[i] = nums[i] + nums[j] - (nums[j] = nums[i]);
    }

然后我们从下标 k 继续开始依次遍历数组的剩余元素。如果元素小于堆顶元素，那么取出堆顶元素，将当前元素入堆。在上面的示例中 ，因为2小于堆顶元素6，所以将2入堆。我们发现现在的完全二叉树不满足大顶堆，所以对其进行调整。

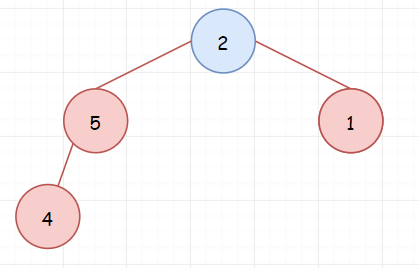
（调整前）

（调整后）

继续重复上述步骤，依次将7,3,8入堆。这里因为7和8都大于堆顶元素5，所以只有3会入堆。

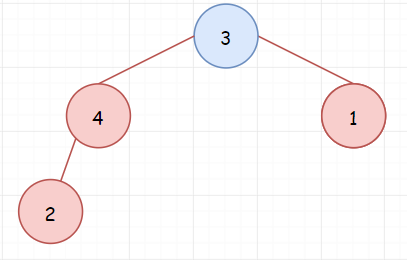
（调整前）

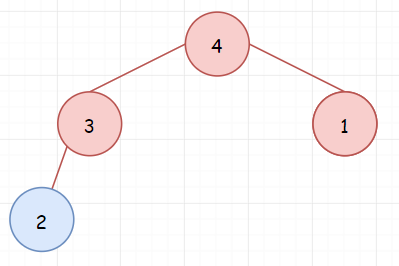
（调整后）

最后得到的堆，就是我们想要的结果。由于堆的大小是 K，所以这里空间复杂度是O(K)，时间复杂度是O(NlogK)。

根据分析，完成代码：

//java
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0)
            return new int[0];
        int len = arr.length;
        if (k == len)
            return arr;

        //对arr数组的前k个数建堆
        int[] heap = new int[k];
        System.arraycopy(arr, 0, heap, 0, k);
        buildHeap(heap);

        //对后面较小的树建堆
        for (int i = k; i < len; i++) {
            if (arr[i] < heap[0]) {
                heap[0] = arr[i];
                heapify(heap, 0);
            }
        }
        //返回这个堆
        return heap;
    }

    private void buildHeap(int[] nums) {
        int lastNode = nums.length - 1;
        int startHeapify = (lastNode - 1) / 2;
        while (startHeapify >= 0) {
            heapify(nums, startHeapify--);
        }
    }

    private void heapify(int[] nums, int i) {
        int len = nums.length;
        if (i >= len)
            return;
        int c1 = ((i << 1) + 1), c2 = ((i << 1) + 2);
        int max = i;
        if (c1 < len && nums[c1] > nums[max]) max = c1;
        if (c2 < len && nums[c2] > nums[max]) max = c2;
        if (max != i) {
            swap(nums, max, i);
            heapify(nums, max);
        }
    }

    private void swap(int[] nums, int i, int j) {
        nums[i] = nums[i] + nums[j] - (nums[j] = nums[i]);
    }
}

大根堆(前 K 小) / 小根堆（前 K 大),Java中有现成的 PriorityQueue，实现起来最简单：\(O(NlogK)\)
本题是求前 K 小，因此用一个容量为 K 的大根堆，每次 poll 出最大的数，那堆中保留的就是前 K 小啦（注意不是小根堆！小根堆的话需要把全部的元素都入堆，那是 \(O(NlogN\))😂，就不是 \(O(NlogK)\)啦～～）
这个方法比快排慢，但是因为 Java 中提供了现成的 PriorityQueue（默认小根堆），所以实现起来最简单，没几行代码～

上面自己实现堆可能有点麻烦，所以我们使用Java自带的PriorityQueue优先队列，它是使用堆来实现的，默认为小顶堆，我们改一下比较器即可。
使用API：

// 保持堆的大小为K，然后遍历数组中的数字，遍历的时候做如下判断：
// 1. 若目前堆的大小小于K，将当前数字放入堆中。
// 2. 否则判断当前数字与大根堆堆顶元素的大小关系，如果当前数字比大根堆堆顶还大，这个数就直接跳过；
//    反之如果当前数字比大根堆堆顶小，先poll掉堆顶，再将该数字放入堆中。
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {

        if (k == 0 || arr.length == 0) {
            return new int[0];  // 返回长度为0的空数组
        }

        // 默认是小根堆，实现大根堆需要重写一下比较器。
        // 我们需要一个容量为k的大顶堆，后面的数字来和顶进行比较，比它小就替换，调整堆
        Queue<Integer> heap = new PriorityQueue<>((v1, v2) -> v2 - v1);

        // 建立一个容量为k的大顶堆
        for (int i = 0; i < k; i++) {
            heap.add(arr[i]);
        }

        // 后面的数字和顶进行比较，比他小就替换，调整堆
        for (int i = k; i < arr.length; i++) {
            if (arr[i] < heap.peek()) {

                heap.remove();
                heap.add(arr[i]);
            }
        }

        // 将队列转化为int[]数组
        return heap.stream().mapToInt(Integer::valueOf).toArray();
    }
}

大佬解法

大佬解法：更多解法

解题思路：
对于经典TopK问题，本文给出 4 种通用解决方案。

一、用快排最最最高效解决 TopK 问题：O(N)

注意找前 K 大/前 K 小问题不需要对整个数组进行 O(NlogN) 的排序！
例如本题，直接通过快排切分排好第 K 小的数（下标为 K-1），那么它左边的数就是比它小的另外 K-1 个数啦～
下面代码给出了详细的注释，没啥好啰嗦的，就是快排模版要记牢哈～

Java

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // 最后一个参数表示我们要找的是下标为k-1的数
        return quickSearch(arr, 0, arr.length - 1, k - 1);
    }

    private int[] quickSearch(int[] nums, int lo, int hi, int k) {
        // 每快排切分1次，找到排序后下标为j的元素，如果j恰好等于k就返回j以及j左边所有的数；
        int j = partition(nums, lo, hi);
        if (j == k) {
            return Arrays.copyOf(nums, j + 1);
        }
        // 否则根据下标j与k的大小关系来决定继续切分左段还是右段。
        return j > k? quickSearch(nums, lo, j - 1, k): quickSearch(nums, j + 1, hi, k);
    }

    // 快排切分，返回下标j，使得比nums[j]小的数都在j的左边，比nums[j]大的数都在j的右边。
    private int partition(int[] nums, int lo, int hi) {
        int v = nums[lo];
        int i = lo, j = hi + 1;
        while (true) {
            while (++i <= hi && nums[i] < v);
            while (--j >= lo && nums[j] > v);
            if (i >= j) {
                break;
            }
            int t = nums[j];
            nums[j] = nums[i];
            nums[i] = t;
        }
        nums[lo] = nums[j];
        nums[j] = v;
        return j;
    }
}

快排切分时间复杂度分析： 因为我们是要找下标为k的元素，第一次切分的时候需要遍历整个数组 (0 ~ n) 找到了下标是 j 的元素，假如 k 比 j 小的话，那么我们下次切分只要遍历数组 (0~k-1)的元素就行啦，反之如果 k 比 j 大的话，那下次切分只要遍历数组 (k+1～n) 的元素就行啦，总之可以看作每次调用 partition 遍历的元素数目都是上一次遍历的 1/2，因此时间复杂度是 N + N/2 + N/4 + ... + N/N = 2N, 因此时间复杂度是 O(N)。

二、大根堆(前 K 小) / 小根堆（前 K 大),Java中有现成的 PriorityQueue，实现起来最简单：O(NlogK)

本题是求前 K 小，因此用一个容量为 K 的大根堆，每次 poll 出最大的数，那堆中保留的就是前 K 小啦（注意不是小根堆！小根堆的话需要把全部的元素都入堆，那是 O(NlogN)😂，就不是 O(NlogK)啦～～）
这个方法比快排慢，但是因为 Java 中提供了现成的 PriorityQueue（默认小根堆），所以实现起来最简单，没几行代码～

Java

// 保持堆的大小为K，然后遍历数组中的数字，遍历的时候做如下判断：
// 1. 若目前堆的大小小于K，将当前数字放入堆中。
// 2. 否则判断当前数字与大根堆堆顶元素的大小关系，如果当前数字比大根堆堆顶还大，这个数就直接跳过；
//    反之如果当前数字比大根堆堆顶小，先poll掉堆顶，再将该数字放入堆中。
class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // 默认是小根堆，实现大根堆需要重写一下比较器。
        Queue<Integer> pq = new PriorityQueue<>((v1, v2) -> v2 - v1);
        for (int num: arr) {
            if (pq.size() < k) {
                pq.offer(num);
            } else if (num < pq.peek()) {
                pq.poll();
                pq.offer(num);
            }
        }
        
        // 返回堆中的元素
        int[] res = new int[pq.size()];
        int idx = 0;
        for(int num: pq) {
            res[idx++] = num;
        }
        return res;
    }
}

三、二叉搜索树也可以 O(NlogK)解决 TopK 问题哦

BST 相对于前两种方法没那么常见，但是也很简单，和大根堆的思路差不多～
要提的是，与前两种方法相比，BST 有一个好处是求得的前K大的数字是有序的。

因为有重复的数字，所以用的是 TreeMap 而不是 TreeSet（有的语言的标准库自带 TreeMultiset，也是可以的）。

TreeMap的key 是数字，value 是该数字的个数。
我们遍历数组中的数字，维护一个数字总个数为 K 的 TreeMap：
1.若目前 map 中数字个数小于 K，则将 map 中当前数字对应的个数 +1；
2.否则，判断当前数字与 map 中最大的数字的大小关系：若当前数字大于等于 map 中的最大数字，就直接跳过该数字；若当前数字小于 map 中的最大数字，则将 map 中当前数字对应的个数 +1，并将 map 中最大数字对应的个数减 1。

Java

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // TreeMap的key是数字, value是该数字的个数。
        // cnt表示当前map总共存了多少个数字。
        TreeMap<Integer, Integer> map = new TreeMap<>();
        int cnt = 0;
        for (int num: arr) {
            // 1. 遍历数组，若当前map中的数字个数小于k，则map中当前数字对应个数+1
            if (cnt < k) {
                map.put(num, map.getOrDefault(num, 0) + 1);
                cnt++;
                continue;
            } 
            // 2. 否则，取出map中最大的Key（即最大的数字), 判断当前数字与map中最大数字的大小关系：
            //    若当前数字比map中最大的数字还大，就直接忽略；
            //    若当前数字比map中最大的数字小，则将当前数字加入map中，并将map中的最大数字的个数-1。
            Map.Entry<Integer, Integer> entry = map.lastEntry();
            if (entry.getKey() > num) {
                map.put(num, map.getOrDefault(num, 0) + 1);
                if (entry.getValue() == 1) {
                    map.pollLastEntry();
                } else {
                    map.put(entry.getKey(), entry.getValue() - 1);
                }
            }
            
        }

        // 最后返回map中的元素
        int[] res = new int[k];
        int idx = 0;
        for (Map.Entry<Integer, Integer> entry: map.entrySet()) {
            int freq = entry.getValue();
            while (freq-- > 0) {
                res[idx++] = entry.getKey();
            }
        }
        return res;
    }
}

四、数据范围有限时直接计数排序就行了：O(N)

Java

class Solution {
    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0 || arr.length == 0) {
            return new int[0];
        }
        // 统计每个数字出现的次数
        int[] counter = new int[10001];
        for (int num: arr) {
            counter[num]++;
        }
        // 根据counter数组从头找出k个数作为返回结果
        int[] res = new int[k];
        int idx = 0;
        for (int num = 0; num < counter.length; num++) {
            while (counter[num]-- > 0 && idx < k) {
                res[idx++] = num;
            }
            if (idx == k) {
                break;
            }
        }
        return res;
    }
}

最后
雷同题目 215. 数组中的第K个最大元素 常考哦～

---

因为分治算法一般都应用于操作树，所以大家可以看看：【数据结构】树

329. 矩阵中的最长递增路径

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

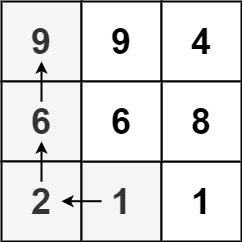
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

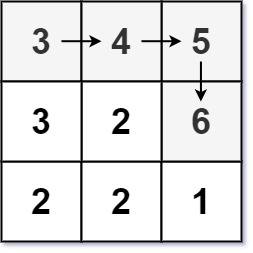
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

深度优先搜索dfs

可以试试加上记忆化搜索来优化。

public class Main {

    public static void main(String[] args) {
        Main main = new Main();
        System.out.println(main.longestIncreasingPath(new int[][]{{9, 9, 4}, {6, 6, 8}, {2, 1, 1}}));
    }

    int[][] matrix;
    public int longestIncreasingPath (int[][] matrix) {
        // write code here
        this.matrix = matrix;
        int max = 0;

        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[i].length; j++) {
                max = Math.max(max, dfs(i, j));
            }
        }
        return max;
    }

    public int dfs(int x, int y) {
        if (check(x, y)) {
            return 0;
        }

        int right = 0, down = 0, left = 0, up = 0, max = 0;
        if (!check(x, y + 1) && matrix[x][y] < matrix[x][y + 1]) {
            right = dfs(x, y + 1);
            max = Math.max(max, right);
        }
        if (!check(x + 1, y) && matrix[x][y] < matrix[x + 1][y]) {
            down = dfs(x + 1, y);
            max = Math.max(max, down);
        }
        if (!check(x, y - 1) && matrix[x][y] < matrix[x][y - 1]) {
            left = dfs(x, y - 1);
            max = Math.max(max, left);
        }
        if (!check(x - 1, y) && matrix[x][y] < matrix[x - 1][y]) {
            up = dfs(x - 1, y);
            max = Math.max(max, up);
        }

        return max + 1;
    }

    public boolean check(int x, int y) {
        return x < 0 || x >= matrix.length || y < 0 || y >= matrix[0].length || matrix[x][y] == -1;
    }
}

记忆化搜索

class Solution {
    int[][] matrix;
    int[][] dp;

    public int longestIncreasingPath (int[][] matrix) {
        // write code here
        this.matrix = matrix;
        this.dp = new int[matrix.length][matrix[0].length];

        int max = 0;
 
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[i].length; j++) {
                max = Math.max(max, dfs(i, j));
            }
        }
        return max;
    }
 
    public int dfs(int x, int y) {
        if (check(x, y)) {
            return 0;
        }
        if (dp[x][y] != 0) {
            return dp[x][y];
        }
 
        int right = 0, down = 0, left = 0, up = 0, max = 0;
        if (!check(x, y + 1) && matrix[x][y] < matrix[x][y + 1]) {
            right = dfs(x, y + 1);
            max = Math.max(max, right);
        }
        if (!check(x + 1, y) && matrix[x][y] < matrix[x + 1][y]) {
            down = dfs(x + 1, y);
            max = Math.max(max, down);
        }
        if (!check(x, y - 1) && matrix[x][y] < matrix[x][y - 1]) {
            left = dfs(x, y - 1);
            max = Math.max(max, left);
        }
        if (!check(x - 1, y) && matrix[x][y] < matrix[x - 1][y]) {
            up = dfs(x - 1, y);
            max = Math.max(max, up);
        }
        dp[x][y] = max + 1;
        return dp[x][y];
    }
 
    public boolean check(int x, int y) {
        return x < 0 || x >= matrix.length || y < 0 || y >= matrix[0].length || matrix[x][y] == -1;
    }
}