【算法】回溯法四步走
回溯法
回溯法:自顶向下、由大及小
动态规划:自底向上、由小及大
对于回溯法,网上有很多种解释,这里我依照自己的(死宅)观点做了以下三种通俗易懂的解释:
-
正经版解释:其实人生就像一颗充满了分支的n叉树,你的每一个选择都会使你走向不同的路线,获得不同的结局。如果能重来,我要选李白~呸!说错了,如果能重来,我们就能回溯到以前,选择到最美好的结局。
-
游戏版解释:玩过互动电影游戏(如 行尸走肉)的都知道,你的每个选择都会影响游戏的结局,掌控他人的生死。每次选择错误导致主角或配角死亡,我们是不是回溯读档,希望得到一个更好的结局。
PS:克莱曼婷天下无敌!
- 动漫版解释:看过主角拥有死亡回归(疯狂暗示486)的都知道,主角的每个选择都能影响大局,可是486直接能回溯重选,这与我们今天要讲的回溯法极其相似。
PS:爱蜜莉雅、雷姆我都要!
- 电影版解释:《大话西游》里有这样的情节,至尊宝要对着「月光宝盒」喊一声「波若菠萝蜜」,时间就可以回到回去(所有的人物、事物都得一样,才能叫「回到过去」),他才能救人。这个道理其实和这里的「撤销选择」是一模一样的。
只有撤销上一次的选择,重置现场,才能够回到 完全一样 的过去,再开始新的尝试才会是有效的。
理解回溯比较困难的是理解「回到过去」,现实世界里我们无法回到过去,但是在算法的世界里可以。
- 总结版解释:从众多分支的路径中,找到符合结果的路径或路径集。
专业名词
- 解空间:即 所有的可能情况
概念
回溯算法:是类似于枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。
它是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术称为回溯法,而满足回溯条件的某个状态的点称为“回溯点”(你也可以理解为存档点)。
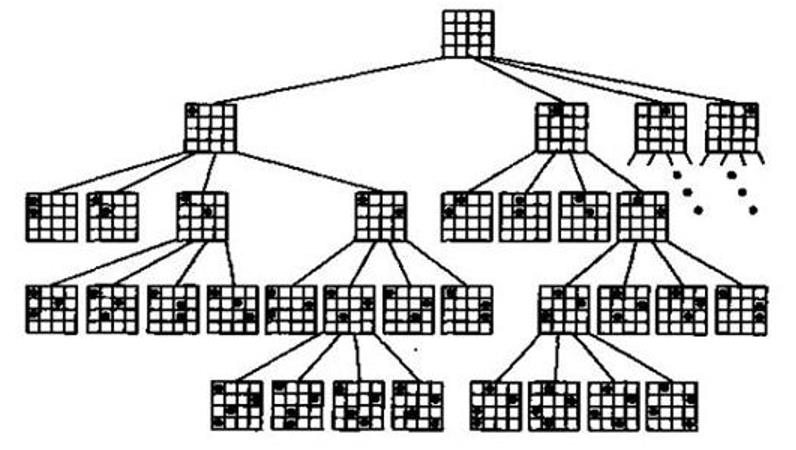
上图为八皇后的解空间树,如果当前点不符合要求就退回再走。
许多复杂的,规模较大的问题都可以使用回溯法,有“通用解题方法”的美称。
基本思想
在包含问题的所有解的解空间树中,按照深度优先搜索的策略,从根结点出发深度探索解空间树。
当探索到某一结点时,要先判断该结点是否包含问题的解:
- 如果包含,就从该结点出发继续探索下去;
- 如果该结点不包含问题的解,则逐层向其祖先结点回溯。(其实回溯法就是对隐式图的深度优先搜索算法)
结束条件:
- 若用回溯法求问题的所有解时,要回溯到根,且根结点的所有可行的子树都要已被搜索遍才结束。
- 若使用回溯法求任一个解时,只要搜索到问题的一个解就可以结束。
网上的一般步骤
虽然我觉得网上的一般步骤太抽象了,但是还是摆在这里供大家参考吧。。
-
针对所给问题,确定问题的解空间:
首先应明确定义问题的解空间,问题的解空间应至少包含问题的一个(最优)解。 -
确定结点的扩展搜索规则:
及时确定规则,并不是每个解空间都要走完才能发现是死路的,有时候走到一半就发现不满足条件了。 -
以深度优先方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索:
不满足条件的路径及时剪掉(即 剪枝),避免继续走下去浪费时间。
类比:比如说削苹果,
我们规定:苹果皮必须不断,要完整地削完整个苹果。
那么,如果我们削到一半苹果皮断掉了,我们就可以直接退回去(即 回溯)换个苹果削了,如果继续削下去,只会浪费时间。
算法框架
问题框架:
设问题的解是一个n维向量(a1,a2,…,an),约束条件是ai(i=1,2,3,…,n)之间满足某种条件,记为 f(ai)。
非递归回溯框架
其中,a[n]为解空间,i为搜索的深度,框架如下:
int a[n],i; //a[n]为解空间,i为深度
初始化数组 a[];
i = 1;
while (i>0(有路可走) and (未达到目标)) { //还未回溯到头
if(i > n) { //搜索到叶结点
搜索到一个解,输出;
} else { //处理第 i 个元素
a[i]第一个可能的值;
while(a[i]在不满足约束条件且在搜索空间内) {
a[i]下一个可能的值;
}//while
if(a[i]在搜索空间内) {
标识占用的资源;
i = i+1; //扩展下一个结点
} else {
清理所占的状态空间; //回溯
i = i – 1;
}//else
}//else
}//while
递归回溯框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单。
其中,a[n]为解空间,i为搜索的深度,框架如下:
int a[n]; //a[n]为解空间
BackTrace(int i) { //尝试函数,i为深度
if(i>n) {
输出结果;
}
for(j = 下界; j <= 上界; j=j+1) { //枚举 i 所有可能的路径
if(check(j)) { //检查满足限界函数和约束条件
a[i] = j;
... //其他操作
BackTrace(i+1);
回溯前的清理工作(如 a[i]置空值等);
}//if
}//for
}//BackTrace
回溯算法与深度优先遍历
以下是维基百科中「回溯算法」和「深度优先遍历」的定义。
回溯法 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案;
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
深度优先搜索 算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会 尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过,搜索将 回溯 到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点,则选择其中一个作为源结点并重复以上过程,整个进程反复进行直到所有结点都被访问为止。
我刚开始学习「回溯算法」的时候觉得很抽象,一直不能理解为什么递归之后需要做和递归之前相同的逆向操作,在做了很多相关的问题以后,我发现其实「回溯算法」与「 深度优先遍历 」有着千丝万缕的联系。
为什么不是广度优先遍历
-
首先是正确性,只有遍历状态空间,才能得到所有符合条件的解,这一点 BFS 和 DFS 其实都可以;
-
在深度优先遍历的时候,不同状态之间的切换很容易 ,可以再看一下上面有很多箭头的那张图,每两个状态之间的差别只有 1 处,因此回退非常方便,这样全局才能使用一份状态变量完成搜索;
-
如果使用广度优先遍历,从浅层转到深层,状态的变化就很大,此时我们不得不在每一个状态都新建变量去保存它,从性能来说是不划算的;
-
如果使用广度优先遍历就得使用队列,然后编写结点类。队列中需要存储每一步的状态信息,需要存储的数据很大,真正能用到的很少 。
-
使用深度优先遍历,直接使用了系统栈,系统栈帮助我们保存了每一个结点的状态信息。我们不用编写结点类,不必手动编写栈完成深度优先遍历。
个人理解
「回溯算法」与「深度优先遍历」都有「不撞南墙不回头」的意思。我个人的理解是:「回溯算法」强调了「深度优先遍历」思想的用途,用一个 不断变化 的变量,在尝试各种可能的过程中,搜索需要的结果。强调了 回退 操作对于搜索的合理性。而「深度优先遍历」强调一种遍历的思想,与之对应的遍历思想是「广度优先遍历」。至于广度优先遍历为什么没有成为强大的搜索算法,我们在题解后面会提。
在「力扣」第 51 题的题解《回溯算法(第 46 题 + 剪枝)》 中,展示了如何使用回溯算法搜索 4 皇后问题的一个解,相信对大家直观地理解「回溯算法」是有帮助。
搜索与遍历
我们每天使用的搜索引擎帮助我们在庞大的互联网上搜索信息。搜索引擎的「搜索」和「回溯搜索」算法里「搜索」的意思是一样的。
搜索问题的解,可以通过 遍历 实现。所以很多教程把「回溯算法」称为爆搜(暴力解法)。因此回溯算法用于 搜索一个问题的所有的解 ,通过深度优先遍历的思想实现。
与动态规划的区别
共同点
用于求解多阶段决策问题。多阶段决策问题即:
- 求解一个问题分为很多步骤(阶段);
- 每一个步骤(阶段)可以有多种选择。
不同点
- 动态规划只需要求我们评估最优值是多少,最优值对应的具体解是什么并不要求。因此很适合应用于评估一个方案的效果;
- 回溯算法可以搜索得到所有的方案(当然包括最优解),但是本质上它是一种遍历算法,时间复杂度很高。
适用场景
回溯法一般使用在问题可以树形化表示时的场景。
这样说明的话可能有点抽象,那么我们来换个方法说明。
当你发现,你的问题需要用到多重循环,具体几重循环你又没办法确定,那么就可以使用我们的回溯算法来将循环一层一层的进行嵌套。
就像这样:
void f(int depth) {
if (depth == max) {
return;
}
for (...) {
f(depth + 1);
}
}
这样套起来的话,无论多少重循环我们都可以满足。
关键词:深度优先遍历、迷宫
回溯四步走
由于上述网上的步骤太抽象了,所以在这里我自己总结了回溯四步走:
由于回溯法一般采用递归方法实现,所以大家可以结合【算法】递归三步走来进行理解。
编写检测函数(非必须)
编写检测函数:检测函数用来检测此路径是否满足题目条件,是否能通过。
这步不做硬性要求。。不一定需要
1. 明确函数功能
1.明确函数功能:要清楚你写这个函数是想要做什么?它的参数是什么?它的全局变量是什么?从何处开始出发?
递归的时候要按照题目的要求来设置函数功能,再根据函数功能来设置函数的参数。
其实我们按照题目要求来设置函数功能,最后总是莫名其妙就把问题给解决了,可能很多人都觉得这也太奇妙了吧。
理解:其实递归的理论基础其实就是制定查找规则,按照这个规则找答案,一定能找到答案。例如,这个题:面试题 04.06. 后继者,做出来之后觉得莫名其妙就找到答案了。
问题:可是如果完全按照题目要求来设置函数功能的话,那根据先序遍历和中序遍历来确定后序遍历函数的方法参数真的能返回一个数组吗?
技巧:
- 全局变量和方法参数:(当前节点状态)这个方法的参数最好由递归时的当前阶段的状态决定!最好这个方法的参数能够记录我们当前阶段(当前节点)的状态!
全局变量:一般为引用类型变量,用于记录结果集,并且时刻记录着当前的状态,需要手动还原现场;
方法参数:一般为基本类型变量,用于记录递归深度、位置坐标、遍历方向等,在方法参数中的递归深度状态可以无需手动还原现场,因为这是调用栈,用完了自己会弹出,还原现场。
注意:我们的递归方法的方法参数,都是为了表明我们所绘树形图的当前节点的状态。
当然,不仅仅是递归方法的方法参数,也包括全局成员变量也可以表示当前节点状态。
(这个当前阶段的状态一般指递归深度depth,而不是第几个分支i,分支选择是由for (int i = 0; i < length; i++)中的i来决定的,不需要我们写入函数参数中。(只是有时候depth和i恰好相等而已)
比如,如果我们这个方法需要实现阶乘,那么我们的方法参数需要记录当前阶乘的数字(即 当前阶段的状态)
基础状态:只是为了递归能够出去,而有的基础状态,是必须的(如果需要其他状态得另外附加)
-
一维状态:递归深度
depth或index,到达一定递归深度就出去- 递归深度
depth,初始值 1,深度范围 1~n,递归出口if (depth > n) - 选择索引
index,初始值 0,索引范围 0~n-1,递归出口if (index >= n)
- 递归深度
-
二维状态:当前位置
(x, y),到达指定位置就出去 -
返回数据:返回数据应该是我们遇到递归出口之后,需要告诉给前一步递归的信息数据!
比如,计算阶乘我们就需要在遇到递归出口之后,告诉我们前一步递归我们现在的结果数据,方便整合。
特别注意:递归函数的返回值最好设置为单个元素,比如说一个节点或者一个数值,告诉前一步递归我们现在的结果数据即可。
如果返回值是数组的话,我们将无法从中提取到任何有效信息来进行操作;
如果结果需要数组的话,我们可以将数组作为公共变量,返回值为void,我们在方法体里面操作数组即可。注意:因为回溯法我们一般只关心叶子结点的结果,中间的过程函数一般没什么返回的作用,所以函数返回值类型一般为void或者boolean,boolean可以为函数返回查找结果。
- 当然,也不排除中间节点返回的结果有作用的情况。不过这种情况也可以用递归函数的方法参数来存放以及利用所有返回的结果。
操作:方法参数 depth,递归出口if (depth > n)
注意:递归深度depth,根节点深度为 0,一般根节点代表的解都为空解,所以深度为 0,之后的解深度为 1 才代表我们的第 1 次分支路径选择。
拿全排列来举例:
设计状态变量
-
首先这棵树除了根结点和叶子结点以外,每一个结点做的事情其实是一样的,即:在已经选择了一些数的前提下,在剩下的还没有选择的数中,依次选择一个数,这显然是一个 递归 结构;
-
递归的终止条件是: 一个排列中的数字已经选够了 ,因此我们需要一个变量来表示当前程序递归到第几层,我们把这个变量叫做 depth,或者命名为 index ,表示当前要确定的是某个全排列中下标为 index 的那个数是多少;
-
布尔数组 used,初始化的时候都为 false 表示这些数还没有被选择,当我们选定一个数的时候,就将这个数组的相应位置设置为 true ,这样在考虑下一个位置的时候,就能够以 \(O(1)\) 的时间复杂度判断这个数是否被选择过,这是一种「以空间换时间」的思想。
这些变量称为「状态变量」,它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。
2. 寻找递归出口
2.寻找递归出口:一般为递归深度,或叶子节点,或非叶子节点(包括根节点)、所有节点等。决定递归出去时要执行的操作。
(递归出口的递归深度如果不确定,那么可以从递归初始深度开始算,到结束的递归深度,深度有多少,即可心中有数)
技巧:递归深度一般起始调用为 1,代表当前操作选择第 1 个元素进行填入。当超过填入元素的限制时,则是递归出口 return;
特别注意:每次提交数组的集合(即
List<List<>>)的时候,都要记得创建一个新的数组来存放结果数组元素(即new List<>(list)),不然后面操作的都是加入集合后的那个数组。
这里需要注意的是,由于我们的节点状态可能需要多个参数来表示,所以我们的递归出口可能也并不唯一,我们有可能需要为每个状态参数来安排一个递归出口,确保我们的递归能够确实有效的出去。
例如:
我们需要注意这里的递归出口:
- 当我们操作一棵树root的时候,我们的递归出口可能是
if (root == null),- 而我们在操作两颗树t1,t2的时候,我们的递归出口应该包括这两棵树所有为null的情况,如
if (t1 == null && t2 == null)和if (t1 == null || t2 == null)这样才能概况完所有为null的出口情况。
技巧:
- 找到结果集并返回的出口先写,因为找到结果集并返回的出口往往更加苛刻,范围更小,先将访问小的出口放前面出去,如
a == true && b == true和a == true,很明显应该先判断前面的。 - 再写因不满足条件而出去的出口
并且值得注意的是,我们的递归出口并不一定都是在最开头的位置,我们一般在最开头设置递归出口是希望递归能以最快的速度出去;
但是有时候我们在对当前节点进行一些相关处理操作之后我们就希望判断一下能不能递归出口,所以递归出口有可能是在代码中间的,大家需要灵活应用。
在这一步,我们需要思考题目需要的解在哪里?是在某一具体的深度、还是在叶子结点、还是在非叶子结点(包括根节点)、还是在每个节点、还是在从跟结点到叶子结点的路径?
-
在某一具体的深度:
if (depth > n) -
在每个节点:
if (true)
面试题 08.04. 幂集
3. 明确所有路径
3.明确所有路径(选择):这个构思路径最好用树形图表示。
而分支路径的选择由 for (int i; i < length; i++)中的 i 来决定的,list.add(i),即 选择第 i 条分支路径。
例如:走迷宫有上下左右四个方向,也就是说我们站在一个点处有四种选择,我们可以画成无限向下延伸的四叉树。
直到向下延伸到叶子节点,那里便是出口;
从根节点到叶子节点沿途所经过的节点就是我们满足题目条件的选择。
操作:f(depth)
- 递归深度:方法参数
depth,递归出口if (depth >= n),递归深度增加f(depth + 1)
注意:递归深度depth,根节点深度为 0,一般根节点代表的解都为空解,所以深度为 0,之后的解深度为 1 才代表我们的第 1 次分支路径选择。
-
所有路径:
for (int i; i < length; i++)即 枚举 i 所有可能的路径 -
路径分支选择:非方法参数,选择 for 循环中的分支路径
i,如list.add(i);
如果不选那就不写list. add(i)就行了,没有i,不用整些花里胡哨的。
注意:****在选择完路径分支之后,一般都伴随着 递归深度 + 1,
f(depth + 1),即 在选择完路径分支之后,我们从根节点向下移了一个深度。特别注意:
depth和i是两个不一样的概念,有时候我们做题把它当成了一个概念,其实只是有时候depth和i恰好相等而已
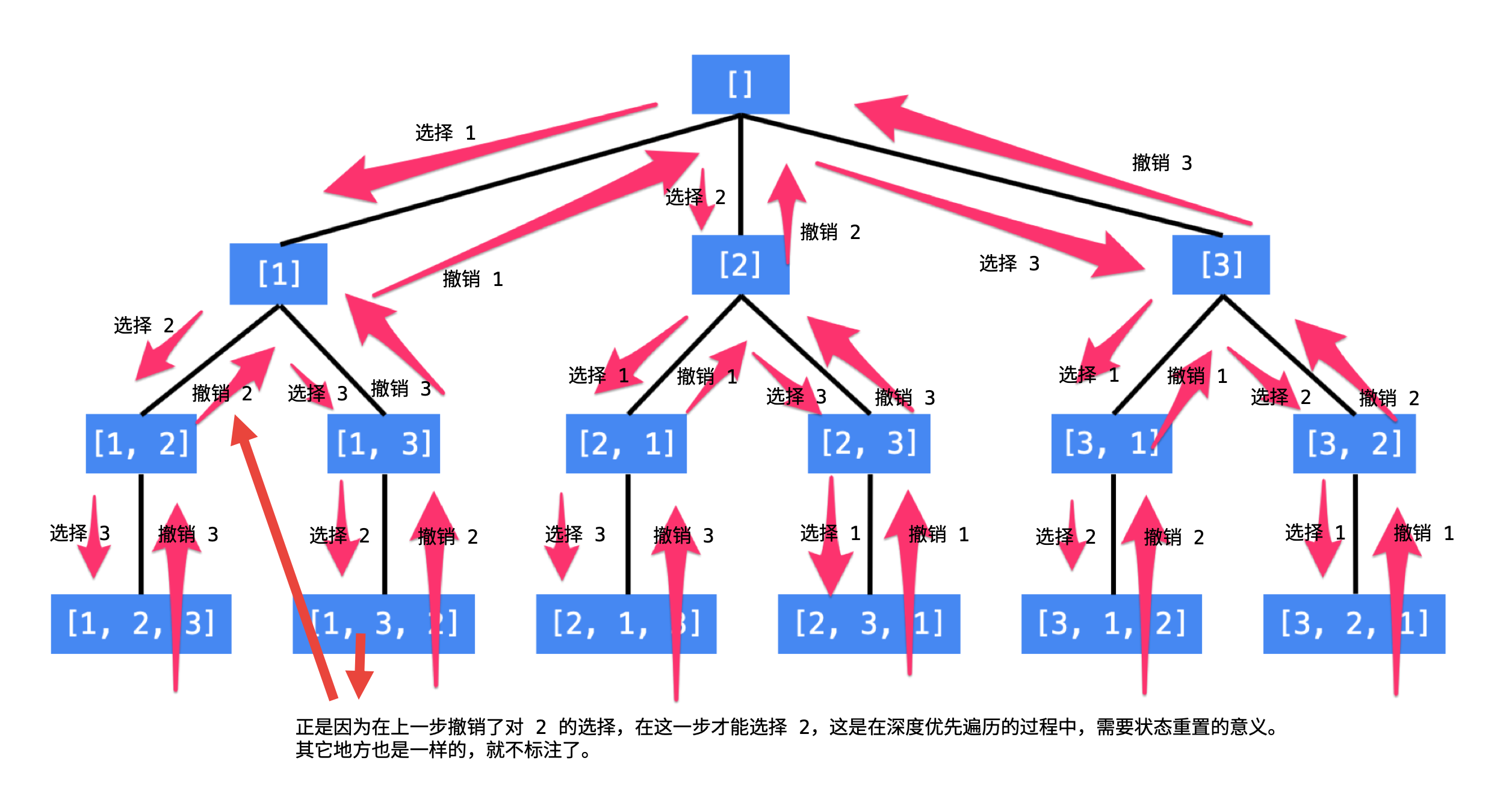
做题的时候,建议 先画树形图 ,画图能帮助我们想清楚递归结构,想清楚如何剪枝。拿题目中的示例,想一想人是怎么做的,一般这样下来,这棵递归树都不难画出。
在画图的过程中思考清楚:
- 分支如何产生;
- 题目需要的解在哪里?是在叶子结点、还是在非叶子结点、还是在从跟结点到叶子结点的路径?
- 哪些搜索会产生不需要的解的?例如:产生重复是什么原因,如果在浅层就知道这个分支不能产生需要的结果,应该提前剪枝,剪枝的条件是什么,代码怎么写?
4. 回溯还原现场
4.回溯还原现场:若该节点所有选择已做完却仍然没有找到出口,那么我们需要回溯还原现场,将该节点重置为初始状态,回溯到一切都没有发生的时候,再退回去。(与递归函数之前的操作对称)
特别注意:这意味着我们使用递归函数那行的前后操作是对称的!
注意:回溯还原现场是必要的,如果不还原现场,那你的回溯有什么意义呢。。类比:大雄出意外了,哆啦A梦坐时空机回到过去想要改变这一切,结果过去的一切都没有被重置到初始状态,回到过去大雄还是现在这种受伤的样子没有改变,那么回到过去有什么意义呢。
补充说明,这里的回溯还原现场对于方法栈内的方法参数或局部变量来说并不一定是必要的,因为我们回溯的时候可以把当前方法栈帧弹出,不会影响到回溯,弹出之后就是还原的现场。
也就是说,我们的方法内使用的是方法参数这种与栈相关的局部变量,我们是不需要回溯还原现场的,因为我们当回溯的时候自动将当前栈帧弹出了,这样就相当于还原现场了。
如 求解一棵树内从根节点出发到任意节点的目标节点和有几个满足目标节点和?
public void f(TreeNode root, int sum) {
if (root == null) {
return;
}
sum -= root.val; // 这是方法参数,局部变量,存在虚拟机栈中,不需要还原现场,因为调用完会自动弹出栈帧。
if (sum == 0) {
res++;
}
f(root.left, sum);
f(root.right, sum);
}
四步走举例
例如:凑算式
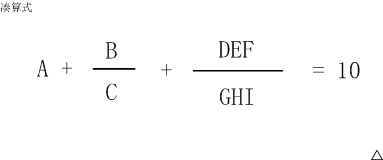
这个算式中AI代表19的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
编写检测函数(非必须)
第一步,写出检测函数,来检测这个路径是否满足条件,是否能通过。
这个函数依据题目要求来编写,当然,如果要求不止一个,可能需要编写多个检测函数。
要做出这个题,
第一步,要写出检测函数
public static int sum = 0; // 用来存放总共的解法数
public static double[] a = new double[10];
// 判断数组里前j个元素是否与t相同
/**
* @param a 传入一个数组a
* @param j 判断前j个元素
* @param t 是否与t相同
* @return
*/
public static boolean same(double[] a, int j, int t) {
for (int i = 1; i < j; i++) {
if (a[i] == t) {
return true;
}
}
return false;
}
/**
* @param a 判断a数组是否满足表达式
* @return 如果满足就true,不满足就false
*/
public static boolean expression(double[] a) {
if ((a[1] + a[2] / a[3] + (a[4] * 100 + a[5] * 10 + a[6]) / (a[7] * 100 + a[8] * 10 + a[9]) == 10))
return true;
else
return false;
}
明确函数功能
由于此题要填数字,所以我们定义 choose(i) 的含义为:在算式中自动填入数字 i 。
寻找递归出口
第二步,要寻找递归出口,当1~9均已填入后,判断表达式是否成立,若成立,则输出。
// 如果选择的数字大于9,则代表1~9均已选完,判断是否满足表达式,输出选择的表达式
if (i > 9) {
if (expression(a)) {
for (int x = 1; x < 10; x++) {
System.out.print(a[x] + " ");
}
System.out.println();
sum++;
}
return;
}
明确所有路径
第三步,要知道这个递归是几个选择,即 几叉树。
此题为1~9九个选择,九条路,九叉树。
for (int j = 1; j <= 9; j++) {
// 如果将要填入的数与前面不冲突,则填入
if (!same(a, i, j)) {
a[i] = j; // 选择分支 j
choose(i + 1); // 递归深度+1
}
}
回溯还原现场
第四步,若该节点没有找到出口,则将当前位置回溯,还原现场,重新选择
在本题中,还原现场即 重置为0(表示还未填入1~9的数字)
for (int j = 1; j <= 9; j++) {
// 如果将要填入的数与前面不冲突,则填入
if (!same(a, i, j)) {
a[i] = j;
choose(i + 1); //递归函数的前后操作对称
//若没有找到出口,则将当前位置重置为0,回溯,还原现场
a[i] = 0; //你看看是不是与a[i]=j是对称的操作
}
}
节点状态参数定义技巧
注意:我们的递归方法的方法参数,都是为了表明我们所绘树形图的当前节点的状态,当然,不仅仅是递归方法的方法参数,也包括全局成员变量也可以表示当前节点状态。
以 depth 表示递归深度(f(depth) 表示第 depth 次选择)
适用场景:一般我们使用这种方法来表示本次 n 叉树的深度,而本次 n 叉树的分支选择是由for ()循环中的 i 来决定的,list.add(i),即 选第 i 条分支。
操作:
- 递归出口:
if (depth >= n) - 分支选择:
list.add(i) - 递归深度增加:
f(depth + 1)
以 start 表示范围区间(f(start) 表示从 start 开始向右选择[start, nums.length - 1])
一般我们使用这种方法来表示不断前进的选择,即 本次选择不会考虑左边之前的选择,从start右边开始选。
适用场景:用于去重,按序选择,避免结果集重复
相当于我们使用start把数组划分为了两个部分,第一个部分就是我们已经选择好的元素,第二部分就是我们还未选择的元素,我们需要做的就是从start开始将还未选择的元素放入左边已选择的元素中(start + 1)。
好处:这样我们可以省去用于存储数组访问情况的
used[]数组,因为我们已选择和未选择已经分开了。
操作:
\([start, nums.length - 1]\):f(start)
- 递归出口:
if (start >= length) - 分支选择:
for (int i = start; i < length; i++)、list.add(i) - 递归深度增加:
f(i + 1)特别注意:这里深度增加的参数为当前选择
i + 1,而不是start + 1。
以 [x][y] 表示完整的当前节点状态(f(x, y) 当前节点状态由 [x, y] 来表示)
适用场景:一般我们使用这种方法来表示树形图上的当前节点的状态,比如说 地图上的索引位置,如 横纵坐标。
操作:
- 递归出口:
if (x < 0 || y < 0 || x >= m || y >= n || used[x][y])越界 - 分支选择:
list. add(nums[x][y]) - 下:
f(x, y + 1) - 右:
f(x + 1, y) - 上:
f(x, y - 1) - 左:
f(x - 1, y)
多种回溯法解法
面试题 08.04. 幂集
幂集。编写一种方法,返回某集合的所有子集。集合中不包含重复的元素。
说明:解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
这里推荐一个大佬的解法:幂集解答
以 depth 表示递归深度
方法一:本题所有节点均为可行解,所以不需要记录深度。
class Solution {
Set<List<Integer>> res = new HashSet<>(); // 结果集合
Set<Integer> set = new TreeSet<>(); // 使用TreeSet来保证集合内元素有序,放入结果集合时方便去重
public List<List<Integer>> subsets(int[] nums) {
f(nums);
return new ArrayList<>(res);
}
// 回溯法
public void f(int[] nums) {
res.add(new ArrayList<>(set));
Integer temp = 0;
for (int i = 0; i < nums.length; i++) {
if (nums[i] != Integer.MAX_VALUE) { // 用过就置为无穷大
temp = nums[i];
set.add(nums[i]);
nums[i] = Integer.MAX_VALUE;
f(nums);
set.remove(temp);
nums[i] = temp;
}
}
}
}
方法二:我们也可以使用二叉树,来用上我们的递归深度:
生成一个\(2^n\)长的数组,数组的值从\(0\)到\(2^{n}-1\)。我们可以把它想象成为一颗二叉树,每个节点的子树都是一个不选0、一个选1
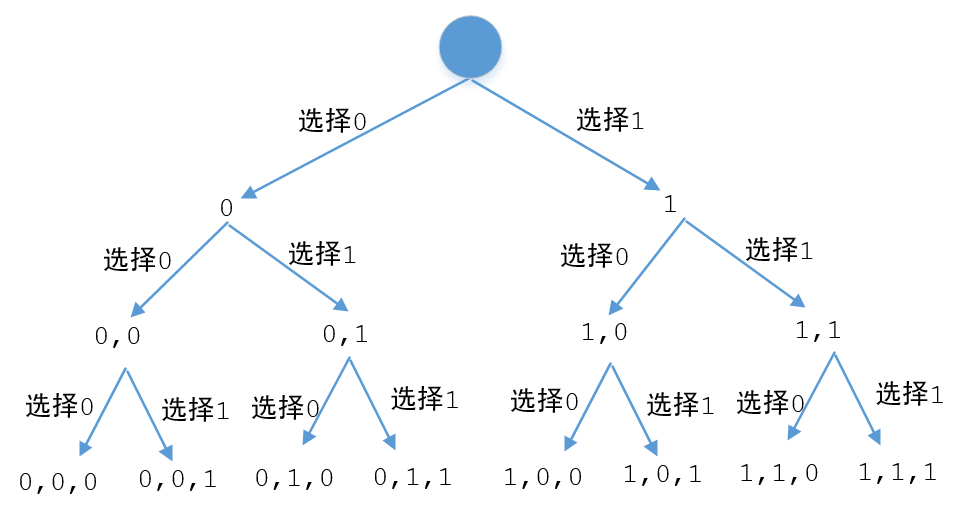
注意:我这里说的是 先不选
0、再选1(即 01,先0后1),这样做的好处就是,我们不需要选了之后还原现场到不选的时候。
所以我们也可以参照这种方式来写,代码如下
List<List<Integer>> res = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
helper(res, nums, new ArrayList<>(), 0);
return res;
}
private void helper(int[] nums, int index) {
// 终止条件判断
if (index == nums.length) {
res.add(new ArrayList<>(list));
return;
}
// 每一个节点都有两个分支,一个选一个不选
// 走不选这个分支,下一个
helper(nums, index + 1); // 不选,直接下一个
// 走选择这个分支
list.add(nums[index]); // 选择
helper(nums, index + 1); // 下一个
// 撤销选择
list.remove(list.size() - 1);
}
以 start 表示范围区间
一般我们使用这种方法来表示不断前进的选择,即 本次选择不会考虑左边之前的选择,从start右边开始选。
相当于我们使用start把数组划分为了两个部分,第一个部分就是我们已经选择好的元素,第二部分就是我们还未选择的元素,我们需要做的就是从start开始将还未选择的元素放入左边已选择的元素中(start + 1)。
好处:这样我们可以省去用于存储数组访问情况的
used[]数组,因为我们已选择和未选择已经分开了。
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> list = new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {
f(nums, 0);
return res;
}
// 回溯法,从start开始选择
public void f(int[] nums, int start) {
res.add(new ArrayList<>(list));
// 从start开始选择
for (int i = start; i < nums.length; i++) {
list.add(nums[i]);
f(nums, i + 1); // 这里需要注意,是i + 1,而不是start + 1
list.remove(list.size() - 1);
}
}
}
以 [x][y] 表示完整的当前状态
本题完整的当前状态不需要参数即可。
如果小伙伴们想看此种情况的示例,可以看看剑指 Offer 13. 机器人的运动范围
优化思路
优化逻辑其实归根结底都是剪枝。
标识遍历过的元素
我们有两种方法可以来标识遍历过的元素,避免重复遍历。
-
修改元素数据为特定值(如
-1、Integer.MAX_VALUE、'\0'),代表已经遍历过;注意:char的
'\0'和0是一样的ASCII值,而不是'0'。(char c = 0等价于char c = '\0') -
可以额外使用
boolean[][] used;来存储遍历过的元素,遍历过就置为true。
剪枝
标志位flag
1.回溯算法可以设置标志位代表找到了,找到了就返回,避免继续回溯浪费时间;
if (flag) {
return;
}
this.flag = true;
方法返回boolean
每个递归节点的结果都返回,每个递归节点的结果状态都关注,而不是返回void像上面标志位一样只关注叶子节点的结果状态。
2.或者说找到了之后我们的方法就返回true,只要有一个true那就代表找到了,所以我们返回使用逻辑或recur(a) || recur(b);
当然,还有一种情况就是,不符合条件我们就返回false,只要有一个false就代表不符合了,所以我们返回使用逻辑与recur(a) && recur(b)。
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);`
return res;
具体剪枝实例可以看下面的《剑指 Offer 12. 矩阵中的路径》
注意:这里可以看到,和我们上面明确函数功能所说的“返回数据”,即 返回数据应该是我们遇到递归出口之后,需要告诉给前一步递归的信息数据!对应上了。
我们需要把这一步找到了或者没找到的boolean信息传递给前一步递归,所以返回类型为boolean。
去重
我们要根据题目的性质,思考如何去除重复的结果,以及如何将去重实现为决策树上的剪枝。
- 有重复元素的子集问题
- 有重复元素的全排列问题
有关上面的去重问题,一般思路都是通过排序来使相等的两个元素紧贴在一起,方便剪枝。
我们的剪枝方法一般为面对重复元素时,从左到右依次选取,若左边的元素没有被选取,那么右边的元素也不能被选取,不能越级。
if (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1]) {
continue;
}
这个判断条件保证了对于重复数的集合,一定是从左往右逐个填入的。
假设我们有 3 个重复数排完序后相邻,那么我们一定保证每次都是拿从左往右第一个未被填过的数字,即整个数组的状态其实是保证了 \([未填入,未填入,未填入]\) 到 \([填入,未填入,未填入]\),再到 \([填入,填入,未填入]\),最后到 \([填入,填入,填入]\) 的过程的,因此可以达到去重的目标。
我们一般也会判断一下当前元素是否被访问过,以免出错
if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
continue;
}
有重复元素的子集问题
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列。
示例 1:
输入:nums = [1,2,2]
输出:[[],[1],[1,2],[1,2,2],[2],[2,2]]
示例 2:
输入:nums = [0]
输出:[[],[0]]
我的方法一:
class Solution {
List<Integer> t = new ArrayList<Integer>();
List<List<Integer>> ans = new ArrayList<List<Integer>>();
int[] nums;
boolean[] visited;
public List<List<Integer>> subsetsWithDup(int[] nums) {
Arrays.sort(nums);
this.nums = nums;
this.visited = new boolean[nums.length];
dfs(0);
return ans;
}
public void dfs(int cur) {
if (cur == nums.length) {
ans.add(new ArrayList<Integer>(t));
return;
}
dfs(cur + 1);
if (cur > 0 && nums[cur - 1] == nums[cur] && !visited[cur - 1]) {
return;
}
t.add(nums[cur]);
visited[cur] = true;
dfs(cur + 1);
visited[cur] = false;
t.remove(t.size() - 1);
}
}
方法二:
class Solution {
List<List<Integer>> result = new ArrayList<>();// 存放符合条件结果的集合
LinkedList<Integer> path = new LinkedList<>();// 用来存放符合条件结果
boolean[] used;
public List<List<Integer>> subsetsWithDup(int[] nums) {
if (nums.length == 0){
result.add(path);
return result;
}
Arrays.sort(nums);
used = new boolean[nums.length];
subsetsWithDupHelper(nums, 0);
return result;
}
private void subsetsWithDupHelper(int[] nums, int startIndex){
result.add(new ArrayList<>(path));
if (startIndex >= nums.length){
return;
}
for (int i = startIndex; i < nums.length; i++){
if (i > 0 && nums[i] == nums[i - 1] && !used[i - 1]){
continue;
}
path.add(nums[i]);
used[i] = true;
subsetsWithDupHelper(nums, i + 1); // 注意递归参数是i + 1,而不是startIndex + 1
path.removeLast();
used[i] = false;
}
}
}
有重复元素的全排列问题
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
答案:
class Solution {
boolean[] vis;
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> ans = new ArrayList<List<Integer>>();
List<Integer> perm = new ArrayList<Integer>();
vis = new boolean[nums.length];
Arrays.sort(nums);
backtrack(nums, ans, 0, perm);
return ans;
}
public void backtrack(int[] nums, List<List<Integer>> ans, int idx, List<Integer> perm) {
if (idx == nums.length) {
ans.add(new ArrayList<Integer>(perm));
return;
}
for (int i = 0; i < nums.length; ++i) {
if (vis[i] || (i > 0 && nums[i] == nums[i - 1] && !vis[i - 1])) {
continue;
}
perm.add(nums[i]);
vis[i] = true;
backtrack(nums, ans, idx + 1, perm);
vis[i] = false;
perm.remove(idx);
}
}
}
记忆化搜索(返回每个递归节点的结果值)
每个递归节点的结果都返回,每个递归节点的结果状态都关注,而不是返回void像上面标志位一样只关注叶子节点的结果状态。
每次递归前进都记录下当前的状态结果,剪掉之前记录过的枝叶,避免重复计算。
记忆化深搜,其实就是对递归dfs暴力的一种优化,将计算过的记录下来,避免重复计算。记忆化深搜也属于DP的一种!
类比:类似于redis的cache缓存,缓存下方法的参数和当前状态结果,分别作为缓存的key和value,下次可以直接取出使用。
如返回值boolean,找到了结果之后我们的方法就返回true,只要有一个true那就代表找到了,所以我们返回使用逻辑或recur(a) || recur(b);
当然,还有一种情况就是,不符合条件我们就返回false,只要有一个false就代表不符合了,所以我们返回使用逻辑与recur(a) && recur(b)。
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) || dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);`
return res;
例如走迷宫,遇到陷阱花费时间为3,要求求出花费时间最短的最优值。
我们就可以在每次递归都记录下当前的状态结果,存在dp[][]数组中;如果当前递归路径递归到该节点所花费时间大于之前记录的状态结果,则剪枝,不必向下继续递归了。
斐波那契数列
给定一个 n,求 斐波那契数列的第 n 项的值,要求用递归实现。
递归
那么,我们只需要套用上面的递归函数,并且处理好递归出口,就能把它写成递归的形式,代码实现如下:
int f(int n) {
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
递归求解的过程如下:
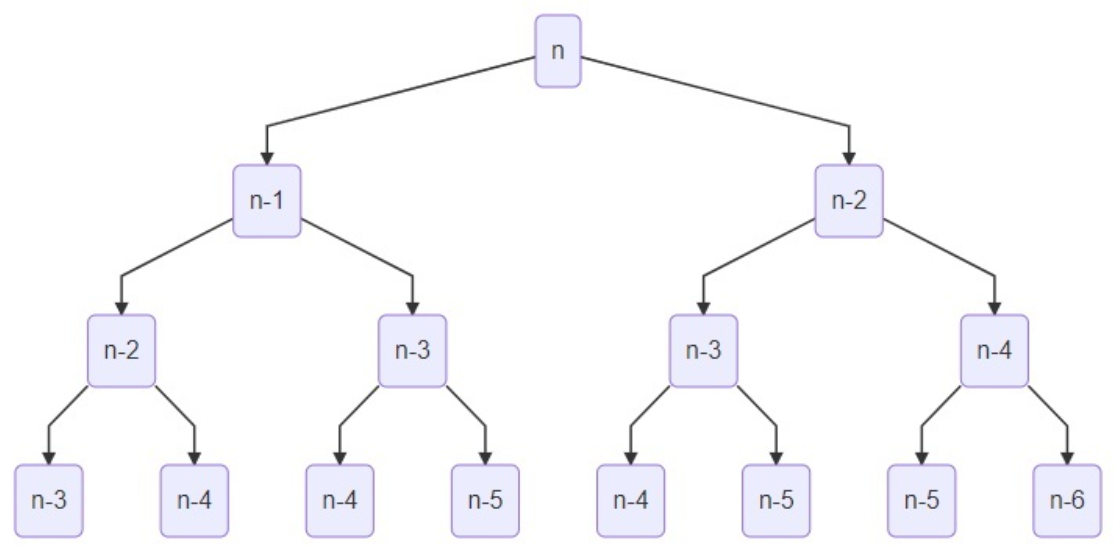
这是一棵二叉树,树的高度为 n,所以粗看递归访问时结点数为 \(2^n\),但是仔细看,对于任何一棵子树而言,左子树的高度一定比右子树的高度大,所以不是一棵严格的完全二叉树。为了探究它实际的时间复杂度,我们改下代码:
int f(int n) {
++c[n]; // count记录每一层递归的次数
if(n <= 1) {
return 1;
}
return f(n-1) + f(n-2);
}
加了一句代码 ++c[n];,引入一个计数器,来看下在 n 为 16 的情况下,不同的 n 的 f(n) 这个函数的调用次数,如图所示:
| n | c[n] |
|---|---|
| 0 | 610 |
| 1 | 987 |
| 2 | 610 |
| 3 | 377 |
| 4 | 233 |
| 5 | 144 |
| 6 | 89 |
| 7 | 55 |
| 8 | 34 |
| 9 | 21 |
| 10 | 13 |
| 11 | 8 |
| 12 | 5 |
| 13 | 3 |
| 14 | 2 |
| 15 | 1 |
| 16 | 1 |
这是一个指数级的算法,随着 的不断增大,时间消耗呈指数级增长,我们在写代码的时候肯定是要避免这样的写法的,尤其是在服务器开发过程中,CPU 是一种极其宝贵的资源,任何的浪费都是可耻的。
记忆化搜索
递归求解斐波那契数列其实是一个深度优先搜索的过程,它是毫无优化的暴力枚举,对于 f(5) 的求解,我们发现,计算过程中其实有很多重叠子问题,例如 f(3) 被计算了 2 次,f(2) 被计算了 3 次,如图所示:
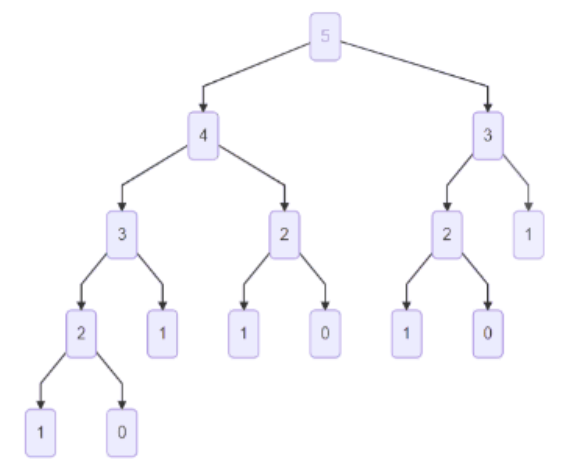
所以如果我们能够确保每个 f(i) 只被计算一次,问题就迎刃而解了。
可以考虑将 f(i) 计算出来的值存储到哈希数组 dp[i] 中,当第二次要访问 f(i) 时,直接取 dp[i] 的值即可,这样每次计算 f(i) 的时间复杂度变成了 \(O(1)\),总共需要计算 f(2),f(3),...,f(n) ,总的时间复杂度就变成了 \(O(n)\) 。
这种用哈希数组来记录运算结果,避免重复运算的方法就是记忆化搜索。
public static int f(int n) {
++c[n];
// 使用缓存记录
if (dp[n] != 0) {
return dp[n];
}
// 递归出口,也是最小问题
if(n <= 1) {
dp[0] = 1;
dp[1] = 1;
return 1;
}
dp[n] = f(n-1) + f(n-2);
return dp[n];
}
来看下在 n 为 16 的情况下,不同的 n 的 f(n) 这个函数的调用次数,如图所示:
| n | c[n] |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 2 |
| 3 | 2 |
| 4 | 2 |
| 5 | 2 |
| 6 | 2 |
| 7 | 2 |
| 8 | 2 |
| 9 | 2 |
| 10 | 2 |
| 11 | 2 |
| 12 | 2 |
| 13 | 2 |
| 14 | 2 |
| 15 | 1 |
| 16 | 1 |
可以看到算法由递归的指数级变为了多项式级,每个值只需计算一次即可,第二次访问无需重复计算,直接取出缓存即可。
https://zhuanlan.zhihu.com/p/438406757
https://blog.csdn.net/qq_54773252/article/details/122800467
练习
下面提供一些我做过的「回溯」算法的问题,以便大家学习和理解「回溯」算法。
题型一:排列、组合、子集相关问题
提示:这部分练习可以帮助我们熟悉「回溯算法」的一些概念和通用的解题思路。解题的步骤是:先画图,再编码。去思考可以剪枝的条件,为什么有的时候用 used 数组,有的时候设置搜索起点 begin 变量,理解状态变量设计的想法。
46. 全排列(中等)
47. 全排列 II(中等):思考为什么造成了重复,如何在搜索之前就判断这一支会产生重复;
39. 组合总和(中等)
40. 组合总和 II(中等)
77. 组合(中等)
78. 子集(中等)
90. 子集 II(中等):剪枝技巧同 47 题、39 题、40 题;
60. 第 k 个排列(中等):利用了剪枝的思想,减去了大量枝叶,直接来到需要的叶子结点;
93. 复原 IP 地址(中等)
题型二:Flood Fill
提示:Flood 是「洪水」的意思,Flood Fill 直译是「泛洪填充」的意思,体现了洪水能够从一点开始,迅速填满当前位置附近的地势低的区域。类似的应用还有:PS 软件中的「点一下把这一片区域的颜色都替换掉」,扫雷游戏「点一下打开一大片没有雷的区域」。
下面这几个问题,思想不难,但是初学的时候代码很不容易写对,并且也很难调试。我们的建议是多写几遍,忘记了就再写一次,参考规范的编写实现(设置 visited 数组,设置方向数组,抽取私有方法),把代码写对。
说明:以下问题都不建议修改输入数据,设置 visited 数组是标准的做法。可能会遇到参数很多,是不是都可以写成成员变量的问题,面试中拿不准的记得问一下面试官
733. 图像渲染(Flood Fill,中等)
200. 岛屿数量(中等)
给你一个由 '1'(陆地)和 '0'(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1
示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:3
我的
class Solution {
char[][] grid;
public int numIslands(char[][] grid) {
this.grid = grid;
int res = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == '1') {
res++;
dfs(i, j);
}
}
}
return res;
}
public void dfs(int x, int y) {
if (x < 0 || x > grid.length - 1 || y < 0 || y > grid[x].length - 1 || grid[x][y] != '1') {
return;
}
grid[x][y] = 0;
dfs(x, y + 1);
dfs(x + 1, y);
dfs(x, y - 1);
dfs(x - 1, y);
}
}
130. 被围绕的区域(中等)
79. 单词搜索(中等)
题型三:字符串中的回溯问题
提示:字符串的问题的特殊之处在于,字符串的拼接生成新对象,因此在这一类问题上没有显示「回溯」的过程,但是如果使用 StringBuilder 拼接字符串就另当别论。
在这里把它们单独作为一个题型,是希望朋友们能够注意到这个非常细节的地方。
17. 电话号码的字母组合(中等),题解;
784. 字母大小写全排列(中等);
22. 括号生成(中等):这道题广度优先遍历也很好写,可以通过这个问题理解一下为什么回溯算法都是深度优先遍历,并且都用递归来写。
题型四:游戏问题
回溯算法是早期简单的人工智能,有些教程把回溯叫做暴力搜索,但回溯没有那么暴力,回溯是有方向地搜索。「力扣」上有一些简单的游戏类问题,解决它们有一定的难度,大家可以尝试一下。
(欢迎大家补充。)
51. N 皇后(困难):其实就是全排列问题,注意设计清楚状态变量,在遍历的时候需要记住一些信息,空间换时间;
37. 解数独(困难):思路同「N 皇后问题」;
488. 祖玛游戏(困难)
529. 扫雷游戏(困难)
回溯嵌套
有时候我们可能需要嵌套循环遍历一棵树,对每一个节点都做一遍前序遍历。所以这也是一种我们需要灵活应用的技巧。
面试题 04.12. 求和路径
给定一棵二叉树,其中每个节点都含有一个整数数值(该值或正或负)。设计一个算法,打印节点数值总和等于某个给定值的所有路径的数量。注意,路径不一定非得从二叉树的根节点或叶节点开始或结束,但是其方向必须向下(只能从父节点指向子节点方向)。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ / \
7 2 5 1
返回:
3
解释:和为 22 的路径有:[5,4,11,2], [5,8,4,5], [4,11,7]
答案一
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int res = 0;
// 一重遍历
public int pathSum(TreeNode root, int sum) {
if (root == null) {
return 0;
}
f(root, sum);
pathSum(root.left, sum);
pathSum(root.right, sum);
return res;
}
// 二重遍历
public void f(TreeNode root, int sum) {
if (root == null) {
return;
}
sum -= root.val;
if (sum == 0) {
res++;
}
f(root.left, sum);
f(root.right, sum);
}
}
答案二
class Solution {
public int pathSum(TreeNode root, int sum) {
if (root == null) {
return 0;
}
return f(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
}
private int f(TreeNode root, int sum) {
if (root == null) {
return 0;
}
int res = sum == root.val ? 1 : 0; // 判断当前节点值是不是目标和
sum -= root.val;
return res + f(root.left, sum) + f(root.right, sum);
}
}
实例
凑算式

这个算式中AI代表19的数字,不同的字母代表不同的数字。
比如:
6+8/3+952/714 就是一种解法,
5+3/1+972/486 是另一种解法。
这个算式一共有多少种解法?
答案:
// 凑算式
public class Sy1 {
public static void main(String[] args) {
// TODO Auto-generated method stub
choose(1);
System.out.println("一共"+sum+"种解法");
}
public static int sum = 0; // 用来存放总共的解法数
public static double[] a = new double[10];
// 判断数组里前j个元素是否与t相同
/**
* @param a 传入一个数组a
* @param j 判断前j个元素
* @param t 是否与t相同
* @return
*/
public static boolean same(double[] a, int j, int t) {
for (int i = 1; i < j; i++) {
if (a[i] == t) {
return true;
}
}
return false;
}
/**
* @param a 判断a数组是否满足表达式
* @return 如果满足就true,不满足就false
*/
public static boolean expression(double[] a) {
if ((a[1] + a[2] / a[3] + (a[4] * 100 + a[5] * 10 + a[6]) / (a[7] * 100 + a[8] * 10 + a[9]) == 10))
return true;
else
return false;
}
/**
* @param i 选择第i个数字 递归
*/
public static void choose(int i) {
// 如果选择的数字大于9,则代表1~9均已选完,输出选择的表达式
if (i > 9) {
if (expression(a)) {
for (int x = 1; x < 10; x++) {
System.out.print(a[x] + " ");
}
System.out.println();
sum++;
}
return;
}
for (int j = 1; j <= 9; j++) { // 明确所有路径
// 如果将要填入的数与前面不冲突,则填入
if (!same(a, i, j)) {
a[i] = j; // 选择分支路径 j
choose(i + 1); // 递归深度+1
//若没有找到出口,则将当前位置重置为0,回溯,还原现场
a[i] = 0;
}
}
}
}
程序运行结果:
3.0 5.0 1.0 9.0 7.0 2.0 4.0 8.0 6.0
4.0 9.0 3.0 5.0 2.0 8.0 1.0 7.0 6.0
5.0 3.0 1.0 9.0 7.0 2.0 4.0 8.0 6.0
5.0 4.0 3.0 7.0 2.0 6.0 1.0 9.0 8.0
5.0 4.0 9.0 7.0 3.0 8.0 1.0 6.0 2.0
5.0 8.0 6.0 4.0 7.0 3.0 1.0 2.0 9.0
6.0 4.0 2.0 3.0 5.0 8.0 1.0 7.0 9.0
6.0 4.0 2.0 7.0 1.0 8.0 3.0 5.0 9.0
6.0 7.0 3.0 4.0 8.0 5.0 2.0 9.0 1.0
6.0 8.0 3.0 9.0 5.0 2.0 7.0 1.0 4.0
6.0 9.0 8.0 4.0 3.0 7.0 1.0 5.0 2.0
7.0 1.0 4.0 9.0 6.0 8.0 3.0 5.0 2.0
7.0 3.0 2.0 8.0 1.0 9.0 5.0 4.0 6.0
7.0 3.0 2.0 9.0 8.0 1.0 6.0 5.0 4.0
7.0 5.0 3.0 2.0 6.0 4.0 1.0 9.0 8.0
7.0 5.0 3.0 9.0 1.0 2.0 6.0 8.0 4.0
7.0 9.0 6.0 3.0 8.0 1.0 2.0 5.0 4.0
7.0 9.0 6.0 8.0 1.0 3.0 5.0 4.0 2.0
8.0 1.0 3.0 4.0 6.0 5.0 2.0 7.0 9.0
8.0 6.0 9.0 7.0 1.0 2.0 5.0 3.0 4.0
8.0 7.0 6.0 1.0 9.0 5.0 2.0 3.0 4.0
9.0 1.0 3.0 4.0 5.0 2.0 6.0 7.0 8.0
9.0 1.0 3.0 5.0 2.0 4.0 7.0 8.0 6.0
9.0 2.0 4.0 1.0 7.0 8.0 3.0 5.0 6.0
9.0 2.0 4.0 3.0 5.0 8.0 7.0 1.0 6.0
9.0 3.0 4.0 1.0 5.0 7.0 6.0 2.0 8.0
9.0 4.0 8.0 1.0 7.0 6.0 3.0 5.0 2.0
9.0 4.0 8.0 3.0 5.0 6.0 7.0 1.0 2.0
9.0 6.0 8.0 1.0 4.0 3.0 5.0 7.0 2.0
一共29种解法
方格填数
如下的10个格子填入0~9的数字。
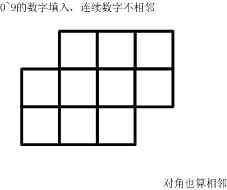
- 要求:连续的两个数字不能相邻。(左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
答案:
// 方格填数
public class Sy2 {
public static void main(String[] args) {
// TODO Auto-generated method stub
Block bk = new Block();
bk.init();
bk.addNum(0);// , 0, 0);
System.out.println("一共"+Block.sum+"种方案");
}
}
class Block {
public int[][] b = new int[3][4];
public static int sum;
/**
* 初始化整个数组
*/
public void init() {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
b[i][j] = -2;
}
}
}
/**
* @param y y行
* @param x x列
* @param n 填数n
* @return 返回此方格是否能填数
*/
public boolean isAble(int y, int x, int n) {
// y行 x列 填数n
if (b[y][x] != -2)
return false;
for (int j = y - 1; j <= y + 1; j++) {
for (int i = x - 1; i <= x + 1; i++) {
if (j < 3 && j >= 0 && i < 4 && i >= 0) {
if (b[j][i] == n - 1 || b[j][i] == n + 1) {
return false;
}
}
}
}
return true;
}
/**
* @param n 填入数字n
*/
public void addNum(int n) {
if (n > 9) {
sum++;
return;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
if ((i == 0 && j == 0) || (i == 2 && j == 3))
continue;
// 如果此方格能填数,则填入数字
if (this.isAble(i, j, n)) {
b[i][j] = n;
this.addNum(n + 1);// , y, x+1);
b[i][j] = -2; // 当加入下一个不行返回后,还原现在方块,继续循环
}
}
}
}
}
程序运行结果:
一共1580种方案
蛙跳河
在一个 5*5 的地图上,一只蛙欲从起点跳到目的地。中间有一条河(如图),但这只蛙不会游泳,并且每次跳只能横着跳一格或者竖着跳一格。(聪明的蛙不会跳已经跳过的路)
- 总共有多少种跳法。
- 给出路径最短的跳法。

答案:
- 明确函数功能:jump(m, n)为跳到(m, n)位置。
- 寻找递归出口:不在边界之内 或 已走过。
- 明确所有路径:右跳、左跳、下跳、上跳
- 回溯还原现场:
path--; // 回溯法关键步骤
a[m][n] = 0;
//青蛙跳
public class Sy1 {
static int count = 0; // 跳法种类计数
static int x = 4, y = 4; // 目的坐标
static int step = 0; // 记录步数
// 地图,0代表没有走过,1 代表已经走过
static int[][] map = { { 0, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0 }, { 1, 1, 0, 1, 1 }, { 0, 0, 0, 0, 0 }, { 0, 0, 0, 0, 0 } };
static int min = 25; // 用来记录最小步数
static int sx[] = new int[25], sy[] = new int[25]; // 记录坐标
// 求解总共跳法,并求出最短步数,方便下面列出路径
static void jump(int m, int n) {
// 该点在地图边界之外或者走过
if (m < 0 || m >= 5 || n < 0 || n >= 5 || map[m][n] != 0) {
return;
}
map[m][n] = 1; // 走到此节点
step++;
if (m == x && n == y) { // 如果到达目的地
if (step < min)// 更新最短步数
min = step;
count++;
}
// 所有路径
jump(m + 1, n); // 右跳
jump(m - 1, n); // 左跳
jump(m, n + 1); // 下跳
jump(m, n - 1); // 上跳
step--; // 回溯法关键步骤
map[m][n] = 0;
}
// 列出最短步数的路径
static void find(int m, int n) {
// 该点在地图边界之外或者走过
if (m < 0 || m >= 5 || n < 0 || n >= 5 || map[m][n] != 0) {
return;
}
// 记录坐标
sx[step] = m;
sy[step] = n;
// 走到此节点
map[m][n] = 1;
step++;
if (m == x && n == y && step == min) { // 到达目的且为最短路径
int p = min - 1;
System.out.print("最短 path:" + p + "步");
for (int i = 0; i < min; i++)
System.out.print("(" + sx[i] + "," + sy[i] + ")");
System.out.println();
}
find(m + 1, n);
find(m - 1, n);
find(m, n + 1);
find(m, n - 1);
step--;
map[m][n] = 0;
}
public static void main(String[] args) {
jump(0, 0);
step = 0;
System.out.println("总共" + count + "种解法");
find(0, 0);
}
}
程序运行结果:

走迷宫
以一个 M×N 的长方阵表示迷宫,0 和 1 分别表示迷宫中的通路和障碍。
设计一个程序,对任意输入的迷宫,输出一条从入口到出口的通路,或得出没有通路的结论。
例:
输入:
请输入迷宫的行数 9
请输入迷宫的列数 8
请输入 9 行 8 列的迷宫
0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0
0 0 1 0 1 1 0 1
0 1 1 1 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 1 0 1
0 1 1 1 1 0 0 1
1 1 0 0 0 1 0 1
1 1 0 0 0 0 0 0
为了方便大家观看,我换成了矩阵:
输出:
有路径
路径如下:
# # 1 0 0 0 1 0
0 # 1 0 0 0 1 0
# # 1 0 1 1 0 1
# 1 1 1 0 0 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
为了方便大家观看,我换成了矩阵:
答案:这里用栈来实现的递归,算是一个新思路。
//迷宫
/*位置类*/
class Position {
int row;
int col;
public Position() {
}
public Position(int row, int col) {
this.col = col;
this.row = row;
}
public String toString() {
return "(" + row + " ," + col + ")";
}
}
/*地图类*/
class Maze {
int maze[][];
private int row = 9;
private int col = 8;
Stack<Position> stack;
boolean p[][] = null;
public Maze() {
maze = new int[15][15];
stack = new Stack<Position>();
p = new boolean[15][15];
}
/*
* 构造迷宫
*/
public void init() {
Scanner scanner = new Scanner(System.in);
System.out.println("请输入迷宫的行数");
row = scanner.nextInt();
System.out.println("请输入迷宫的列数");
col = scanner.nextInt();
System.out.println("请输入" + row + "行" + col + "列的迷宫");
int temp = 0;
for(int i = 0; i < row; ++i) {
for(int j = 0; j < col; ++j) {
temp = scanner.nextInt();
maze[i][j] = temp;
p[i][j] = false;
}
}
}
/*
* 回溯迷宫,查看是否有出路
*/
public void findPath() {
// 给原始迷宫的周围加一圈围墙
int temp[][] = new int[row + 2][col + 2];
for(int i = 0; i < row + 2; ++i) {
for(int j = 0; j < col + 2; ++j) {
temp[0][j] = 1;
temp[row + 1][j] = 1;
temp[i][0] = temp[i][col + 1] = 1;
}
}
// 将原始迷宫复制到新的迷宫中
for(int i = 0; i < row; ++i) {
for(int j = 0; j < col; ++j) {
temp[i + 1][j + 1] = maze[i][j];
}
}
// 从左上角开始按照顺时针开始查询
int i = 1;
int j = 1;
p[i][j] = true;
stack.push(new Position(i, j));
while (!stack.empty() && (!(i == (row) && (j == col)))) {
if ((temp[i][j + 1] == 0) && (p[i][j + 1] == false)) {
p[i][j + 1] = true;
stack.push(new Position(i, j + 1));
j++;
} else if ((temp[i + 1][j] == 0) && (p[i + 1][j] == false)) {
p[i + 1][j] = true;
stack.push(new Position(i + 1, j));
i++;
} else if ((temp[i][j - 1] == 0) && (p[i][j - 1] == false)) {
p[i][j - 1] = true;
stack.push(new Position(i, j - 1));
j--;
} else if ((temp[i - 1][j] == 0) && (p[i - 1][j] == false)) {
p[i - 1][j] = true;
stack.push(new Position(i - 1, j));
i--;
} else {
stack.pop();
if(stack.empty()) {
break;
}
i = stack.peek().row;
j = stack.peek().col;
}
}
Stack<Position> newPos = new Stack<Position>();
if (stack.empty()) {
System.out.println("没有路径");
} else {
System.out.println("有路径");
System.out.println("路径如下:");
while (!stack.empty()) {
Position pos = new Position();
pos = stack.pop();
newPos.push(pos);
}
}
/*
* 图形化输出路径
* */
String resault[][]=new String[row+1][col+1];
for(int k=0; k<row; ++k) {
for(int t=0; t<col; ++t) {
resault[k][t]=(maze[k][t])+"";
}
}
while (!newPos.empty()) {
Position p1=newPos.pop();
resault[p1.row-1][p1.col-1]="#";
}
for(int k=0; k<row; ++k) {
for(int t=0; t<col; ++t) {
System.out.print(resault[k][t]+"\t");
}
System.out.println();
}
}
}
/*主类*/
class Sy4 {
public static void main(String[] args) {
Maze demo = new Maze();
demo.init();
demo.findPath();
}
}
程序运行结果:
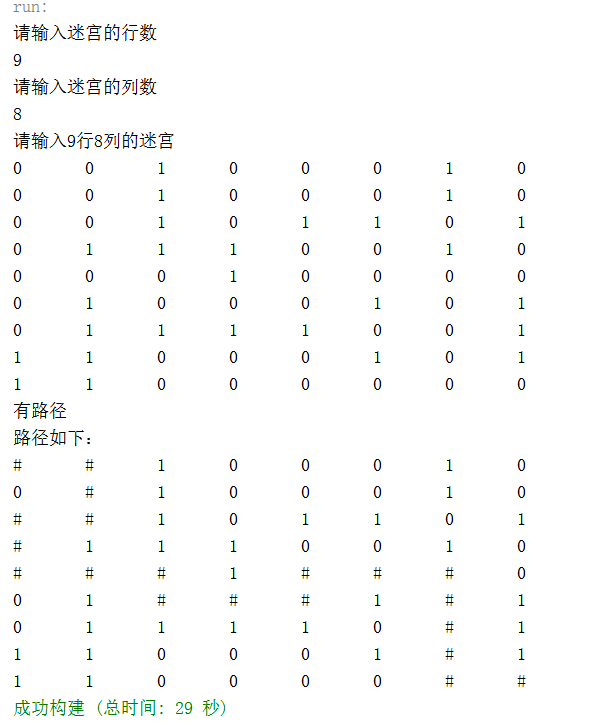
嘿嘿,上面的那种用栈来实现递归的方法是不是看完了呢!把它放在第一个就是为了让大家以为没有递归回溯的答案,好认认真真的看完。。。(别打我)
贴心的我当然准备了用递归回溯方法的代码:
// 迷宫
class Sy4 {
public static void main(String[] args) {
Demo demo = new Demo();
demo.init();
demo.find(0, 0);
}
}
class Demo {
int m, n;
// 类在实例化时分配空间,但是只是逻辑上连续的空间,而不一定是物理上,毕竟有静态变量,不可能完全连续。
String[][] maze; //不能用char,扫描器Scanner不能扫描。
//这里只是声明,后面输入m、n时才能确定分配空间的大小
//初始化迷宫
public void init() {
Scanner scanner = new Scanner(System.in);
System.out.println("请输入迷宫的行数");
m = scanner.nextInt();
System.out.println("请输入迷宫的列数");
n = scanner.nextInt();
maze = new String[m][n];
System.out.println("请输入" + m + "行" + n + "列的迷宫");
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
maze[i][j] = scanner.next();
}
}
System.out.println("--------------------------------------------------------");
System.out.println("迷宫如下:");
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
System.out.print(maze[i][j] + " ");
}
System.out.println();
}
System.out.println("--------------------------------------------------------");
}
//走到(x, y)点,找找路径
public void find(int x, int y) {
if (x < 0 || y < 0 || x >= m || y >= n || !maze[x][y].equals("0")) { // 注意字符串要用equals
return;
}
maze[x][y] = "#"; // 走到此节点
if (x == m - 1 && y == n - 1) {
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
System.out.print(maze[i][j] + " ");
}
System.out.println();
}
System.out.println("--------------------------------------------------------");
}
find(x + 1, y); //下移
find(x - 1, y); //上移
find(x, y + 1); //右移
find(x, y - 1); //左移
maze[x][y] = "0";
}
}
程序运行结果:
--------------------------------------------------------
迷宫如下:
0 0 1 0 0 0 1 0
0 0 1 0 0 0 1 0
0 0 1 0 1 1 0 1
0 1 1 1 0 0 1 0
0 0 0 1 0 0 0 0
0 1 0 0 0 1 0 1
0 1 1 1 1 0 0 1
1 1 0 0 0 1 0 1
1 1 0 0 0 0 0 0
--------------------------------------------------------
# 0 1 0 0 0 1 0
# 0 1 0 0 0 1 0
# 0 1 0 1 1 0 1
# 1 1 1 # # 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# 0 1 0 0 0 1 0
# 0 1 0 0 0 1 0
# 0 1 0 1 1 0 1
# 1 1 1 0 0 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# 0 1 0 0 0 1 0
# # 1 0 0 0 1 0
# # 1 0 1 1 0 1
# 1 1 1 # # 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# 0 1 0 0 0 1 0
# # 1 0 0 0 1 0
# # 1 0 1 1 0 1
# 1 1 1 0 0 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# # 1 0 0 0 1 0
0 # 1 0 0 0 1 0
# # 1 0 1 1 0 1
# 1 1 1 # # 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# # 1 0 0 0 1 0
0 # 1 0 0 0 1 0
# # 1 0 1 1 0 1
# 1 1 1 0 0 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# # 1 0 0 0 1 0
# # 1 0 0 0 1 0
# 0 1 0 1 1 0 1
# 1 1 1 # # 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
# # 1 0 0 0 1 0
# # 1 0 0 0 1 0
# 0 1 0 1 1 0 1
# 1 1 1 0 0 1 0
# # # 1 # # # 0
0 1 # # # 1 # 1
0 1 1 1 1 0 # 1
1 1 0 0 0 1 # 1
1 1 0 0 0 0 # #
--------------------------------------------------------
马走日
假设国际象棋棋盘有 5*5 共 25 个格子。
设计一个程序,使棋子从初始位置(棋盘编号为 1 的位)开始跳马,能够把棋盘的格子全部都走一遍,每个格子只允许走一次。
- 输出一个如图 2 的解,左上角为第一步起点。
- 总共有多少解。
PS:国际象棋的棋子是在格子中间的。国际象棋中的“马走日”,如下图所示,第一步为[1,1],
第二步为[2,8]或[2,12],第三步可以是[3,5]或[3,21]等,以此类推。
答案:
- 明确函数功能:jump(m, n)为跳到(m, n)位置。
- 寻找递归出口:不在边界之内 或 已走过。
- 明确所有路径:8个方位,
技巧:这里可以用一个数组存入八个方位的变化,再用循环依次取出,比写八个方位要聪明许多。
- 回溯还原现场:
path--; // 回溯法关键步骤
a[m][n] = 0;
//马走日
class Sy2 {
private static int[][] next = { { 1, 2 }, { 1, -2 }, { -1, 2 }, { -1, -2 }, { 2, 1 }, { 2, -1 }, { -2, 1 }, { -2, -1 } }; // 马的跳跃路径(技巧)
private static int[][] map; // 地图
private static int m, n;
private static int count = 0;// 统计有多少种走法
private static int step = 0;
public static void main(String[] args) {
m = 5;
n = 5;
int x = 0;
int y = 0;
map = new int[m][n];
jump(x, y);
System.out.println("---------");
System.out.println(count);
}
private static void jump(int x, int y) {
// 如果超出界限,那就继续下一轮
if (x < 0 || x >= m || y < 0 || y >= n || map[x][y] != 0) {
return;
}
// 立足此节点
step++;
map[x][y] = step;
if (step == m * n) {
if (count == 0) // 如果是第一次,那就输出一个
show(map);
count++;
}
// 写出所有路径(技巧)
int tx = 0, ty = 0;
for (int i = 0; i < 8; i++) {
tx = x + next[i][0]; // 技巧
ty = y + next[i][1];
jump(tx, ty);
}
// 还原
step--;
map[x][y] = 0;
}
// 显示数组
private static void show(int[][] arr) {
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
System.out.print(arr[i][j] + " \t");
}
System.out.println();
}
}
}
程序运行结果:
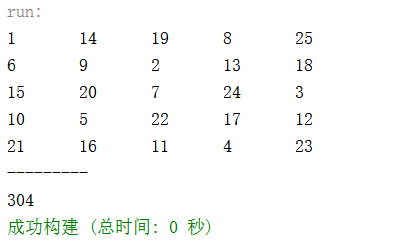
八皇后
编程解决“八皇后问题”:即 在一个 8*8 的矩形格子中排放 8 个皇后。
要满足的条件包括:任意两个皇后不能在同一行,同一列,也不能在同一条对角线上。
要求编程给出解的个数。
答案:
算法原理:回溯法
首先,可归纳问题的条件为,8 皇后之间需满足:
- 不在同一行上
- 不在同一列上
- 不在同一斜线上
- 不在同一反斜线上
这为我们提供一种遍历的思路,我们可以逐行或者逐列来进行可行摆放方案的遍历,每一行(列)遍历出一个符合条件的位置,接着就到下一行(列)遍历下一个棋子的合适位置,这种遍历思路可以保证我们遍历过程中有一个条件是绝对符合的——就是下一个棋子的摆放位置与前面的棋子不在同一行(列)。
这里我们逐列摆放,数组下标代表列号,用数组元素存放行号。
把当前列 N 的前面的某一列设为 m,则 m 的所有取值为{m>=0,m<N}的集合,故又可在上面式子的基础,归纳为如下:
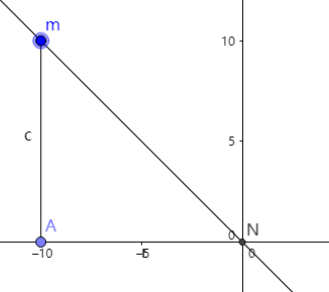
从这个图可以看出,m和N若在同一斜线上,那么行差Am和列差AN应该相等。

所以,在点m存在的情况下,与点m列差为d的点,若行差也为±d,那么就在一条斜线上,不合法。
- cols[N] != cols[m](与第 m 列的棋子不在同一行)
- cols[N] != cols[m] - (N-m) (>=0 ,与第 m 列的棋子不在同一斜线上)
- cols[N] != cols[m] + (N-m) (<=8-1,与第 m 列的棋子不在同一反斜线上)
我们规定当 row[i]=true 时,表示该列第 i 行不能放棋子。
总结:
- 编写检测函数:正如上面的分析,每摆一个,将不合法的位置用数组标识,就不涉足了。当然,也可以写成函数,不过没有数组快。
- 明确函数功能:put(n)为摆第n个皇后。
- 寻找递归出口:当摆完第八个皇后;不同行、不同斜线、不同反斜线。
- 明确所有路径:八行。
- 回溯还原现场:不需要还原,没有破坏现场,因为检测的时候提前用数组标识了,所以不合法的现场都没涉足。
这样我们就能写成下列程序段了:
// 八皇后
class Sy6 {
public static int num = 0; // 累计方案总数
public static final int MAXQUEEN = 8;// 皇后个数,同时也是棋盘行列总数
public static int[] cols = new int[MAXQUEEN]; // 定义cols数组,表示8列棋子摆放情况,数组元素存放行号
public Sy6() {
// 核心函数
put(0);
System.out.println(MAXQUEEN + "皇后问题有" + num + "种摆放方法。");
}
public void put(int n) {
// 当摆完第八个皇后,摆第九个时
if (n > MAXQUEEN - 1) {
// 累计方案个数
num++;
return;
}
// 遍历该列所有不合法的行,并用 rows 数组记录,不合法即 rows[i]=true
boolean[] rows = new boolean[MAXQUEEN];
for (int i = 0; i < n; i++) {
rows[cols[i]] = true; // 同行不合法
int d = n - i; // 列差
if (cols[i] - d >= 0) // 判断是否超界
// 行差为-d的斜线点,不合法
rows[cols[i] - d] = true;
if (cols[i] + d <= MAXQUEEN - 1)// 判断是否超界
// 行差为d的斜线点,不合法
rows[cols[i] + d] = true;
}
// 所有路径:八行都能摆
for (int i = 0; i < MAXQUEEN; i++) {
// 判断该行是否合法,如果不合法,那就继续下一轮
if (rows[i])
continue;
// 设置当前列合法棋子所在行数
cols[n] = i;
// 摆放下一个
put(n + 1);
}
}
public static void main(String args[]) {
Sy6 queen = new Sy6();
}
}
程序运行结果:

二维数组回溯
import java.util.Scanner;
public class 八皇后 {
static int nnn=8;
static int sum=0;
static int x[][]=new int[nnn][nnn];
public static void main(String args[]){
Scanner sc=new Scanner(System.in);
backtrace(0);
System.out.println(sum);
}
static void backtrace(int t){
if(t>=nnn){
sum++;
for(int i=0;i<nnn;i++){
for(int j=0;j<nnn;j++)
System.out.print(x[i][j]+" ");
System.out.println();
}
}
else{
for(int j=0;j<nnn;j++)
if(check(t,j)){
x[t][j]=1;
backtrace(t+1);
x[t][j]=0;
}
}
}
static boolean check(int m,int n){
for(int i=0;i<m;i++){
if(x[i][n]==1)
return false;
}
for(int i=0;i<n;i++){
if(x[m][i]==1)
return false;
}
for(int i=0;i<m;i++)
for(int j=0;j<n;j++){
if(x[i][j]==1&&Math.abs(m-i)==Math.abs(n-j))
return false;
}
for(int i=0;i<m;i++)
for(int j=nnn-1;j>n;j--){
if(x[i][j]==1&&Math.abs(m-i)==Math.abs(n-j))
return false;
}
return true;
}
}
54. 螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:
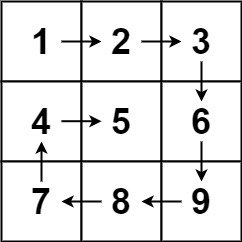
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
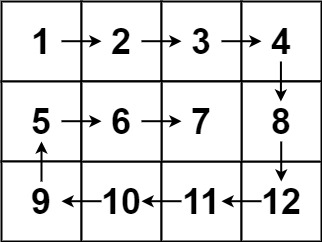
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
答案
一看到这道题,就感觉和遍历二叉树一样,所以直接想到了递归方法,只需要记录数组的当前元素位置以及方向即可。
-
明确函数功能:我们需要用这个函数来前进,并且记录我们经过的元素。
当前状态:当前的行列位置、当前的行进方向。
方法参数有:需要遍历的数组、当前的行列位置、当前的行进方向、用来存放记录我们经过的元素的列表。
返回类型:遇到递归出口之后,需要告诉给前一步递归的信息数据为更改之后的行进方向 -
寻找递归出口:当到达边界,或者已经遍历过了,就出去。
-
明确所有路径:逆时针路径,右、下、左、上,只有到达边界才能变换方向
-
回溯还原现场:这里现场破坏就破坏了,没必要还原。
class Solution {
List<Integer> list = new ArrayList<>();
public List<Integer> spiralOrder(int[][] matrix) {
f(matrix, 0, 0, 0);
return list;
}
// 试试递归,参数有 数组,开始位置x,y,方向,存储的List,返回方向
/**
*
* @param matrix:数组
* @param x:当前行位置
* @param y:当前列位置
* @param direction:0右,1下,2左,3上
* @param list:用来存放记录我们经过的元素,结果数据
* @return:返回方向,用来给下一次遍历指明方向
*/
public int f(int[][] matrix, int x, int y, int direction) {
if (x >= matrix.length || x < 0 || y >= matrix[x].length || y < 0 || matrix[x][y] == Integer.MAX_VALUE) { //碰壁,或者为0遍历过了
return (direction + 1) % 4;
}
// System.out.print(matrix[x][y]);
list.add(matrix[x][y]);
matrix[x][y] = Integer.MAX_VALUE;
// 特别注意:这里需要遍历两次
// 第一次遍历是为了确定一直前进的方向
// 第二次遍历是为了及时修改方向继续前进
// 比如说向上的时候遇到了遍历过的元素,然后回溯回退,结果到了最后return了,所以我们得在它回溯回退回来的时候,加一层前进方向,看看有没有遍历完,能不能继续前进
for (int i = 0; i < 2; i++) {
switch (direction) {
case 0:
direction = f(matrix, x, y + 1, direction);
break;
case 1:
direction = f(matrix, x + 1, y, direction);
break;
case 2:
direction = f(matrix, x, y - 1, direction);
break;
case 3:
direction = f(matrix, x - 1, y, direction);
break;
}
}
return direction;
}
}
迭代答案:
大佬写的
// 试试迭代
class Solution {
public List<Integer> spiralOrder(int[][] matrix) {
List<Integer> result = new ArrayList<Integer>();
if (matrix.length == 0) {
return result;
}
// 设置上下左右边界
int left = 0, right = matrix[0].length - 1, up = 0, down = matrix.length - 1;
// 当前位置
int x = 0, y = 0;
while (left <= right && up <= down) {
for (y = left; y <= right && avoid(left,right,up,down); y++) {
result.add(matrix[x][y]);
}
y--;
up++;
for (x = up; x <= down && avoid(left,right,up,down); x++) {
result.add(matrix[x][y]);
}
x--;
right--;
for (y = right; y >= left && avoid(left,right,up,down); y--) {
result.add(matrix[x][y]);
}
y++;
down--;
for (x = down; x >= up && avoid(left,right,up,down); x--) {
result.add(matrix[x][y]);
}
x++;
left++;
}
return result;
}
// up <= down && left <= right,这是避免碰壁的条件
public boolean avoid(int left, int right, int up, int down) {
return up <= down && left <= right;
}
}
剑指 Offer 13. 机器人的运动范围
地上有一个m行n列的方格,从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动,它每次可以向左、右、上、下移动一格(不能移动到方格外),也不能进入行坐标和列坐标的数位之和大于k的格子。例如,当k为18时,机器人能够进入方格 [35, 37] ,因为3+5+3+7=18。但它不能进入方格 [35, 38],因为3+5+3+8=19。请问该机器人能够到达多少个格子?
示例 1:
输入:m = 2, n = 3, k = 1
输出:3
示例 2:
输入:m = 3, n = 1, k = 0
输出:1
答案
class Solution {
public int m;
public int n;
public int k;
public int res = 0;
public boolean[][] used;
public int movingCount(int m, int n, int k) {
this.m = m;
this.n = n;
this.k = k;
used = new boolean[m][n];
dfs(0, 0);
return res;
}
public void dfs(int x, int y) {
if (x >= m || y >= n || sum(x) + sum(y) > k || used[x][y]) {
return;
}
used[x][y] = true;
res++;
dfs(x, y + 1);
dfs(x + 1, y);
// 只用向右、向下走即可遍历完所有,不需要向左、向上
// dfs(x, y - 1);
// dfs(x - 1, y);
}
public int sum(int x) {
int sum = 0;
while (x != 0) {
sum += x % 10;
x /= 10;
}
return sum;
}
}
剑指 Offer 38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]
答案
class Solution {
public Set<String> set = new HashSet<>();
public StringBuilder sb = new StringBuilder();
public int[] used = null; // 记录遍历过的字符索引,遍历过为1,没遍历过为0
public String[] permutation(String s) {
if (s == null) {
return new String[0];
}
used = new int[s.length()];
f(s, 0);
return new ArrayList<String>(set).toArray(new String[set.size()]);
}
// 递归回溯
// 状态参数:当前在字符串哪一个位置index,当前字符串
public void f(String s, int index) {
if (index > s.length() - 1) {
set.add(sb.toString());
return;
}
// 明确所有路径
// 遍历字符串中所有字符,一个一个放入该index位置
for (int i = 0; i < s.length(); i++) {
if (used[i] > 0) {
continue;
}
// 加入字符
sb.append(s.charAt(i));
used[i]++;
f(s, index + 1);
// 还原现场
used[i]--;
sb.deleteCharAt(sb.length() - 1);
}
}
}
剑指 Offer 12. 矩阵中的路径
请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一格开始,每一步可以在矩阵中向左、右、上、下移动一格。如果一条路径经过了矩阵的某一格,那么该路径不能再次进入该格子。例如,在下面的3×4的矩阵中包含一条字符串“bfce”的路径(路径中的字母用加粗标出)。
[["a","b","c","e"],
["s","f","c","s"],
["a","d","e","e"]]
但矩阵中不包含字符串“abfb”的路径,因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后,路径不能再次进入这个格子。
示例 1:
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
示例 2:
输入:board = [["a","b"],["c","d"]], word = "abcd"
输出:false
答案(flag)
我们使用flag代表已找到,剪枝;并且使用used数组指明访问过的元素。
class Solution {
public char[][] board;
public String word;
public char[] chars;
public boolean[][] used;
public boolean flag; // 找到了,就不用递归了
public boolean exist(char[][] board, String word) {
this.board = board;
this.word = word;
this.chars = word.toCharArray();
used = new boolean[board.length][board[0].length];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
dfs(0, i, j);
}
}
return flag;
}
// 走迷宫,递归回溯法
// 状态:当前位置x、y,当前字符在字符串中的索引index
public void dfs(int index, int x, int y) {
if (index > word.length() - 1) {
this.flag = true;
return;
}
if (x < 0 || x > board.length - 1 || y < 0 || y > board[0].length - 1 || used[x][y] || flag || board[x][y] != chars[index] ) {
return;
}
used[x][y] = true;
index++;
// 开始右下左上
dfs(index, x, y + 1); // 右
dfs(index, x + 1, y); // 下
dfs(index, x, y - 1); // 左
dfs(index, x - 1, y); // 上
used[x][y] = false;
}
}
答案(返回true)
// 之前的算法(不是上面的,上面我加了flag进行优化),我与别人的差距在于,别人找到了就直接跳出递归了,而我还要一直找下去,直到遍历完
// 现在是第二种优化方案!
class Solution {
public char[][] board;
public String word;
public char[] chars;
public boolean[][] used;
public boolean exist(char[][] board, String word) {
this.board = board;
this.word = word;
this.chars = word.toCharArray();
used = new boolean[board.length][board[0].length];
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (dfs(0, i, j)) {
return true;
}
}
}
return false;
}
// 走迷宫,递归回溯法
// 状态:当前位置x、y,当前字符在字符串中的索引index
public boolean dfs(int index, int x, int y) {
if (index > word.length() - 1) {
return true;
}
if (x < 0 || x > board.length - 1 || y < 0 || y > board[0].length - 1 || used[x][y] || board[x][y] != chars[index] ) {
return false;
}
used[x][y] = true;
index++;
// 开始右下左上
boolean res = dfs(index, x, y + 1) || dfs(index, x + 1, y) || dfs(index, x, y - 1) || dfs(index, x - 1, y);
used[x][y] = false;
return res;
}
}
使用'\0'代表已访问
我们使用返回值true代表已找到,剪枝;并且使用'\0'指明访问过的元素。
class Solution {
public boolean exist(char[][] board, String word) {
char[] words = word.toCharArray();
for(int i = 0; i < board.length; i++) {
for(int j = 0; j < board[0].length; j++) {
if(dfs(board, words, i, j, 0)) return true;
}
}
return false;
}
boolean dfs(char[][] board, char[] word, int i, int j, int k) {
if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != word[k]) return false;
if(k == word.length - 1) return true;
board[i][j] = '\0';
boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i , j - 1, k + 1);
board[i][j] = word[k];
return res;
}
}
46. 全排列
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
我的答案
这个答案应该是一般人的第一个思路。
将元素一个一个填入排列结果中,如果元素填过了,那就做个记号,下次不填了,填其他的。
递归函数功能为:选择第n个数字填入,直到将所有数字填入完。
class Solution {
/*
本题采用回溯法
*/
int[] nums;
// 使用list来存放一次排列的结果
List<Integer> list = new ArrayList<>();
// 使用lists来存放全排列结果
List<List<Integer>> lists = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
this.nums = nums;
function(1);
return lists;
}
/*
count为排列中的数字个数,已选数字的个数
*/
public void function(int count) {
int temp = 0; // 临时变量,用来记录初始数据,方便还原现场
// 递归出口,当排列中的数字个数大于所有数字个数时,即 排列完成
if (count > nums.length) {
lists.add(new ArrayList<Integer>(list));
return;
}
// 分支路径
for (int i = 0; i < nums.length; i++) {
if (nums[i] == Integer.MAX_VALUE) {
continue;
}
// 加入排列
list.add(nums[i]);
// 存放原始数据,方便还原现场
temp = nums[i];
// 已经排过的元素标为Integer.MAX_VALUE
nums[i] = Integer.MAX_VALUE;
// 递归函数,其前后操作对称
function(count + 1);
// 还原现场
nums[i] = temp; // 与标为Integer.MAX_VALUE对称
list.remove(list.size() - 1); // 与add加入排列对称
}
}
}
答案
从索引0开始交换,包括自己和自己交换。
从全排列问题开始理解回溯算法
我们尝试在纸上写 3 个数字、4 个数字、5 个数字的全排列,相信不难找到这样的方法。以数组 [1, 2, 3] 的全排列为例。
- 先写以 1 开头的全排列,它们是:[1, 2, 3], [1, 3, 2],即 1 + [2, 3] 的全排列(注意:递归结构体现在这里);
- 再写以 2 开头的全排列,它们是:[2, 1, 3], [2, 3, 1],即 2 + [1, 3] 的全排列;
- 最后写以 3 开头的全排列,它们是:[3, 1, 2], [3, 2, 1],即 3 + [1, 2] 的全排列。
总结搜索的方法:按顺序枚举每一位可能出现的情况,已经选择的数字在 当前 要选择的数字中不能出现。按照这种策略搜索就能够做到 不重不漏。这样的思路,可以用一个树形结构表示。
看到这里的朋友,建议先尝试自己画出「全排列」问题的树形结构。
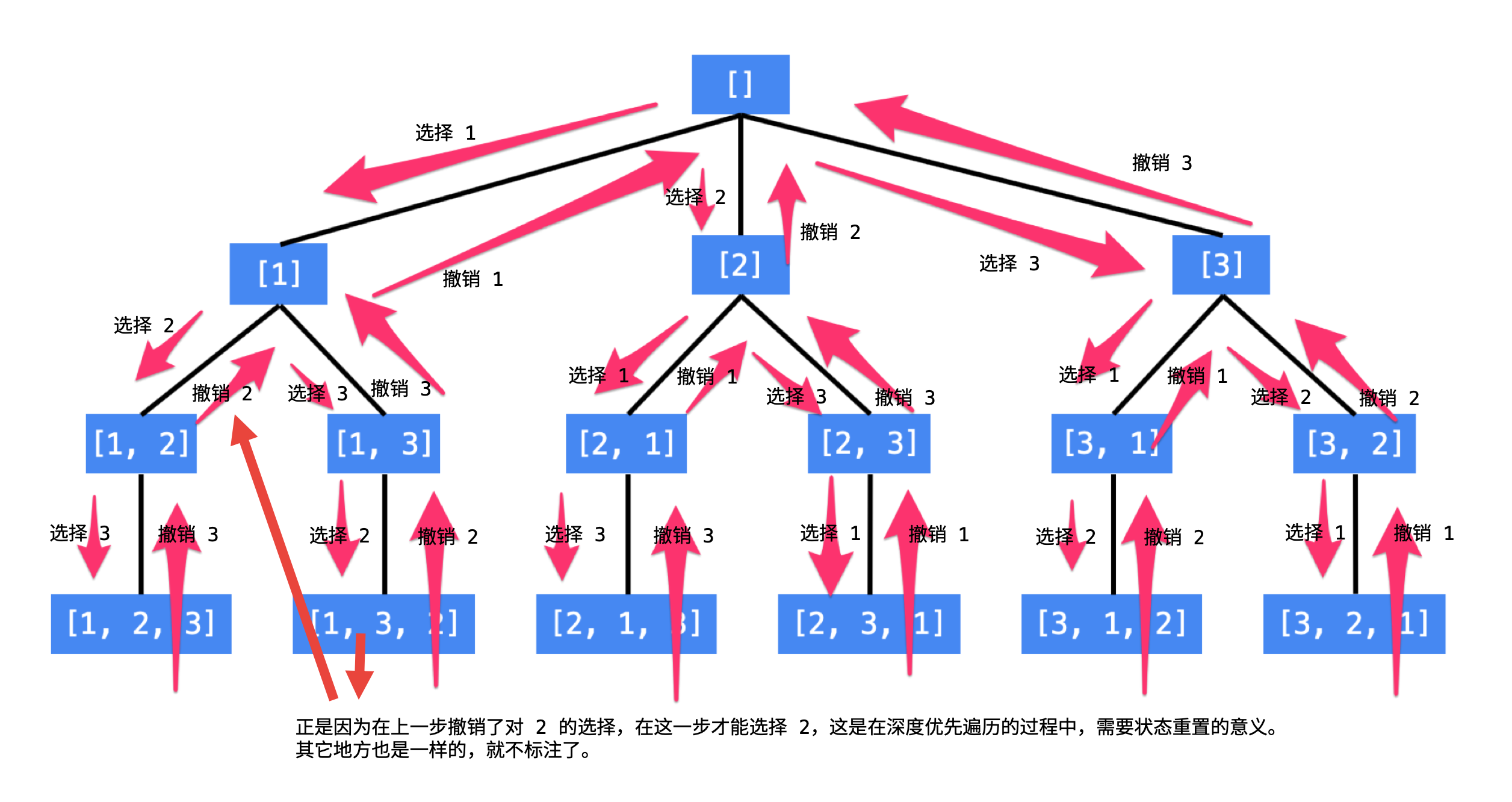
说明:
- 每一个结点表示了求解全排列问题的不同的阶段,这些阶段通过变量的「不同的值」体现,这些变量的不同的值,称之为「状态」;
- 使用深度优先遍历有「回头」的过程,在「回头」以后, 状态变量需要设置成为和先前一样 ,因此在回到上一层结点的过程中,需要撤销上一次的选择,这个操作称之为「状态重置」;
- 深度优先遍历,借助系统栈空间,保存所需要的状态变量,在编码中只需要注意遍历到相应的结点的时候,状态变量的值是正确的,具体的做法是:往下走一层的时候,path 变量在尾部追加,而往回走的时候,需要撤销上一次的选择,也是在尾部操作,因此 path 变量是一个栈;
- 深度优先遍历通过「回溯」操作,实现了全局使用一份状态变量的效果。
使用编程的方法得到全排列,就是在这样的一个树形结构中完成 遍历,从树的根结点到叶子结点形成的路径就是其中一个全排列。
设计状态变量
- 首先这棵树除了根结点和叶子结点以外,每一个结点做的事情其实是一样的,即:在已经选择了一些数的前提下,在剩下的还没有选择的数中,依次选择一个数,这显然是一个 递归 结构;
- 递归的终止条件是: 一个排列中的数字已经选够了 ,因此我们需要一个变量来表示当前程序递归到第几层,我们把这个变量叫做 depth,或者命名为 index ,表示当前要确定的是某个全排列中下标为 index 的那个数是多少;
- 布尔数组 used,初始化的时候都为 false 表示这些数还没有被选择,当我们选定一个数的时候,就将这个数组的相应位置设置为 true ,这样在考虑下一个位置的时候,就能够以 \(O(1)\) 的时间复杂度判断这个数是否被选择过,这是一种「以空间换时间」的思想。
这些变量称为「状态变量」,它们表示了在求解一个问题的时候所处的阶段。需要根据问题的场景设计合适的状态变量。
思路和算法
这个问题可以看作有 n 个排列成一行的空格,我们需要从左往右依此填入题目给定的 n 个数,每个数只能使用一次。那么很直接的可以想到一种穷举的算法,即从左往右每一个位置都依此尝试填入一个数,看能不能填完这 n 个空格,在程序中我们可以用「回溯法」来模拟这个过程。
我们定义递归函数 backtrack(first, output) 表示从左往右填到第 \(\textit{first}\) 个位置,当前排列为 \(\textit{output}\)。 那么整个递归函数分为两个情况:
如果 \(\textit{first}==n\),说明我们已经填完了 n 个位置(注意下标从 0 开始),找到了一个可行的解,我们将 \(\textit{output}\) 放入答案数组中,递归结束。
如果 \(\textit{first}<n\),我们要考虑这第 \(\textit{first}\) 个位置我们要填哪个数。根据题目要求我们肯定不能填已经填过的数,因此很容易想到的一个处理手段是我们定义一个标记数组 \(\textit{vis}[]\) 来标记已经填过的数,那么在填第 \(\textit{first}\) 个数的时候我们遍历题目给定的 n 个数,如果这个数没有被标记过,我们就尝试填入,并将其标记,继续尝试填下一个位置,即调用函数 backtrack(first + 1, output)。回溯的时候要撤销这一个位置填的数以及标记,并继续尝试其他没被标记过的数。
使用标记数组来处理填过的数是一个很直观的思路,但是可不可以去掉这个标记数组呢?毕竟标记数组也增加了我们算法的空间复杂度。
答案是可以的,我们可以将题目给定的 n 个数的数组 \(\textit{nums}\) 划分成左右两个部分,左边的表示已经填过的数,右边表示待填的数,我们在回溯的时候只要动态维护这个数组即可。
具体来说,假设我们已经填到第 \(\textit{first}\) 个位置,那么 \(\textit{nums}\) 数组中 \([0,\textit{first}-1]\) 是已填过的数的集合,\([\textit{first},n-1]\) 是待填的数的集合。我们肯定是尝试用 \([\textit{first},n-1]\) 里的数去填第 \(\textit{first}\) 个数,假设待填的数的下标为 i ,那么填完以后我们将第 i 个数和第 \(\textit{first}\) 个数交换,即能使得在填第 \(\textit{first}+1\)个数的时候 \(\textit{nums}\) 数组的\([0,first]\) 部分为已填过的数,\([\textit{first}+1,n-1]\) 为待填的数,回溯的时候交换回来即能完成撤销操作。
举个简单的例子,假设我们有 [2, 5, 8, 9, 10] 这 5 个数要填入,已经填到第 3 个位置,已经填了 [8,9] 两个数,那么这个数组目前为 [8, 9 | 2, 5, 10] 这样的状态,分隔符区分了左右两个部分。假设这个位置我们要填 10 这个数,为了维护数组,我们将 2 和 10 交换,即能使得数组继续保持分隔符左边的数已经填过,右边的待填 [8, 9, 10 | 2, 5] 。
当然善于思考的读者肯定已经发现这样生成的全排列并不是按字典序存储在答案数组中的,如果题目要求按字典序输出,那么请还是用标记数组或者其他方法。
由于是不重复的全排列,所以我们采用交换法就可以了。
我们维护一个[1,2,3]数组,从第一个开始,交换到最后一个,两两交换。
方法:交换省去标志数组
一般我们使用这种方法来表示不断前进的选择,即 本次选择不会考虑左边之前的选择,从start右边开始选。
相当于我们使用start把数组划分为了两个部分,第一个部分就是我们已经选择好的元素,第二部分就是我们还未选择的元素,我们需要做的就是从start开始将还未选择的元素放入左边已选择的元素中(start + 1)。
好处:这样我们可以省去用于存储数组访问情况的
used[]数组,因为我们已选择和未选择已经分开了。
即 以first为界限,first左边为排好序的元素,first右边为未排好序的元素,我们需要从右边挑选出元素放入左边。
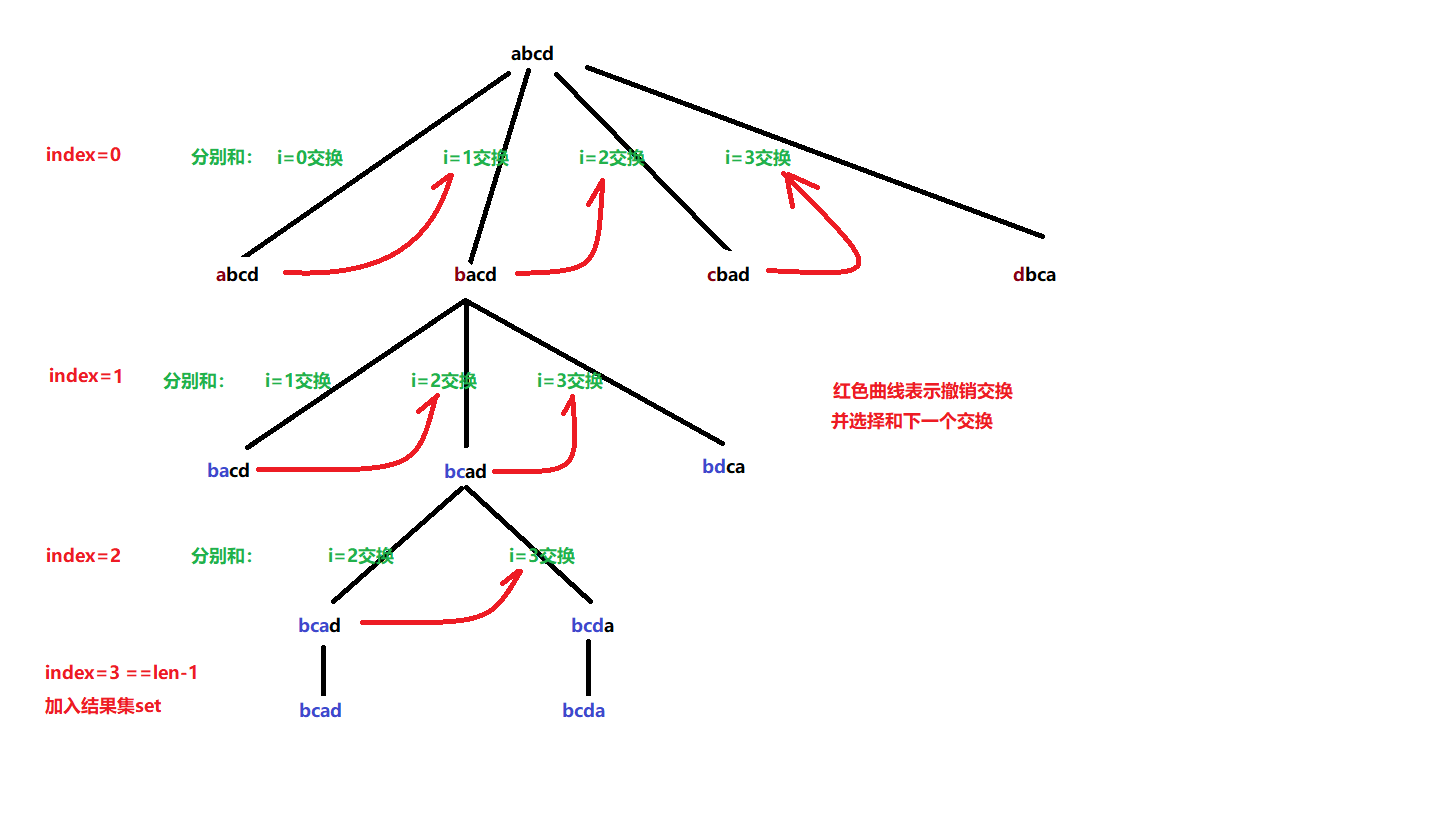
递归函数功能为:选择一个数字填入索引为i的排列数组中,直到将排列数组填满。
class Solution {
int[] nums;
List<Integer> output = new ArrayList<Integer>();
List<List<Integer>> res = new ArrayList<List<Integer>>();
public List<List<Integer>> permute(int[] nums) {
this.nums = nums;
for (int num : nums) {
output.add(num);
}
backtrack(0);
return res;
}
public void backtrack(int first) {
// 所有数都填完了
if (first >= nums.length) {
res.add(new ArrayList<Integer>(output));
return;
}
for (int i = first; i < nums.length; i++) {
// 动态维护数组
Collections.swap(output, first, i);
// 继续递归填下一个数
backtrack(first + 1);
// 撤销操作
Collections.swap(output, first, i);
}
}
}
面试题 08.07. 无重复字符串的排列组合
无重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合,字符串每个字符均不相同。
示例1:
输入:S = "qwe"
输出:["qwe", "qew", "wqe", "weq", "ewq", "eqw"]
示例2:
输入:S = "ab"
输出:["ab", "ba"]
我的
class Solution {
public char[] chars;
List<String> res = new ArrayList<>();
StringBuilder sb = new StringBuilder();
public String[] permutation(String S) {
this.chars = S.toCharArray();
dfs(1);
return res.toArray(new String[res.size()]);
}
// 选择
public void dfs(int depth) {
if (depth > chars.length) {
res.add(sb.toString());
return;
}
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '\0') {
continue;
}
char temp = chars[i];
sb.append(chars[i]);
chars[i] = '\0';
dfs(depth + 1);
sb.delete(sb.length() - 1, sb.length());
chars[i] = temp;
}
}
}
答案
class Solution {
StringBuilder sb = new StringBuilder();
List<String> list = new ArrayList<>();
boolean[] used;
public String[] permutation(String S) {
used = new boolean[S.length()];
f(S, 0);
return list.toArray(new String[list.size()]);
}
public void f(String S, int depth) {
if (depth >= S.length()) {
list.add(sb.toString());
}
for (int i = 0; i < S.length(); i++) {
if (!used[i]) {
sb.append(S.charAt(i));
used[i] = true;
f(S, depth + 1);
sb.delete(sb.length() - 1, sb.length());
used[i] = false;
}
}
}
}
面试题 08.08. 有重复字符串的排列组合
有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。
示例1:
输入:S = "qqe"
输出:["eqq","qeq","qqe"]
示例2:
输入:S = "ab"
输出:["ab", "ba"]
答案
class Solution {
StringBuilder sb = new StringBuilder();
Set<String> list = new HashSet<>();
boolean[] used;
public String[] permutation(String S) {
used = new boolean[S.length()];
f(S, 0);
return list.toArray(new String[list.size()]);
}
public void f(String S, int depth) {
if (depth >= S.length()) {
list.add(sb.toString());
}
for (int i = 0; i < S.length(); i++) {
if (!used[i]) {
sb.append(S.charAt(i));
used[i] = true;
f(S, depth + 1);
sb.delete(sb.length() - 1, sb.length());
used[i] = false;
}
}
}
}
方法二:交换省去标志数组
即 以index为界限,index左边为排好序的元素,index右边为未排好序的元素,我们需要从右边挑选出元素放入左边。
class Solution {
public String[] permutation(String s) {
Set<String> res = new HashSet<>();
char[] C = s.toCharArray();
backtrack(0, C, res);
String[] ans = new String[res.size()];
int i = 0;
for (String str : res) ans[i++] = str;
return ans;
}
private void backtrack(int index, char[] S, Set<String> res) {
if(index == S.length - 1) {
res.add(String.valueOf(S));
return;
}
for(int i = index; i < S.length; i++) {
swap(index, i, S);
backtrack(index + 1, S, res);
swap(index, i, S);
}
}
private void swap(int i, int j,char[] C) {
char temp = C[i];
C[i] = C[j];
C[j] = temp;
}
}
面试题 08.10. 颜色填充
编写函数,实现许多图片编辑软件都支持的「颜色填充」功能。
待填充的图像用二维数组 image 表示,元素为初始颜色值。初始坐标点的行坐标为 sr 列坐标为 sc。需要填充的新颜色为 newColor 。
「周围区域」是指颜色相同且在上、下、左、右四个方向上存在相连情况的若干元素。
请用新颜色填充初始坐标点的周围区域,并返回填充后的图像。
示例:
输入:
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出:[[2,2,2],[2,2,0],[2,0,1]]
解释:
初始坐标点位于图像的正中间,坐标 (sr,sc)=(1,1) 。
初始坐标点周围区域上所有符合条件的像素点的颜色都被更改成 2 。
注意,右下角的像素没有更改为 2 ,因为它不属于初始坐标点的周围区域。
答案
class Solution {
int color;
public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
color = image[sr][sc];
return f(image, sr, sc, newColor);
}
public int[][] f(int[][] image, int sr, int sc, int newColor) {
if (sr < 0 || sr >= image.length || sc < 0 || sc >= image[0].length || image[sr][sc] != color || image[sr][sc] == newColor) {
return image;
}
image[sr][sc] = newColor;
// 上
image = f(image, sr - 1, sc, newColor);
// 左
image = f(image, sr, sc - 1, newColor);
// 下
image = f(image, sr + 1, sc, newColor);
// 右
image = f(image, sr, sc + 1, newColor);
return image;
}
}
面试题 08.09. 括号
括号。设计一种算法,打印n对括号的所有合法的(例如,开闭一一对应)组合。
说明:解集不能包含重复的子集。
例如,给出 n = 3,生成结果为:
[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]
深度,括号匹配数
我们第一眼就可以看出这是一个回溯法的运用,那么我们需要明确函数功能,确定它的参数。
首先深度是必要的,我们需要记录什么时候递归出去;然后我们需要一个数去记录左括号与右括号是否匹配。
我们的节点状态有两种表达方式:
- 深度,括号匹配数:深度为括号总数,括号匹配数遇到左括号+1,遇到右括号-1,直到0。
- 左括号数,右括号数:左右括号数。
这题就是说明递归出口不一定唯一的最好例子,因为我们有多个状态参数。
class Solution {
int n;
List<String> res = new ArrayList<>();
StringBuilder sb = new StringBuilder();
public List<String> generateParenthesis(int n) {
this.n = n;
f(1, 0);
return res;
}
// depth为递归深度(当前填入第几个括号),count为左右括号配比,左括号+1,右括号-1
public void f(int depth, int count) {
// 找到答案先出去
if (depth > 2 * n && count == 0) {
res.add(new String(sb));
return;
}
if (depth > 2 * n || count < 0) {
return;
}
sb.append("(");
f(depth + 1, count + 1);
sb.delete(sb.length() - 1, sb.length());
// sb.deleteCharAt(sb.length() - 1);
sb.append(")");
f(depth + 1, count - 1);
sb.delete(sb.length() - 1, sb.length());
}
}
左括号数,右括号数
我们下面采用第二种状态:
class Solution {
int n;
List<String> res = new ArrayList<>();
StringBuilder sb = new StringBuilder();
public List<String> generateParenthesis(int n) {
this.n = n;
f(0, 0, 0);
return res;
}
// depth为递归深度,count为左右括号配比,左括号+1,右括号-1
public void f(int depth, int left, int right) {
if (left > n || right > n || left < right) {
return;
}
if (depth >= 2 * n && left == n && right == n) {
res.add(new String(sb));
return;
}
sb.append("(");
f(depth + 1, left + 1, right);
sb.delete(sb.length() - 1, sb.length());
sb.append(")");
f(depth + 1, left, right + 1);
sb.delete(sb.length() - 1, sb.length());
}
}
面试题 04.10. 检查子树
检查子树。你有两棵非常大的二叉树:T1,有几万个节点;T2,有几万个节点。设计一个算法,判断 T2 是否为 T1 的子树。
如果 T1 有这么一个节点 n,其子树与 T2 一模一样,则 T2 为 T1 的子树,也就是说,从节点 n 处把树砍断,得到的树与 T2 完全相同。
注意:此题相对书上原题略有改动。
示例1:
输入:t1 = [1, 2, 3], t2 = [2]
输出:true
示例2:
输入:t1 = [1, null, 2, 4], t2 = [3, 2]
输出:false
我的
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
boolean flag = false;
public boolean checkSubTree(TreeNode t1, TreeNode t2) {
if(t2 == null) { // 子树为空
return true;
}
if(t1 == null && t2 != null) { // 子树不为空
return false;
}
isSame(t1, t2);
checkSubTree(t1.left, t2);
checkSubTree(t1.right, t2);
return flag;
}
public void isSame(TreeNode t1, TreeNode t2) {
if (t1 == null && t2 == null) {
flag = true;
return;
}
// 不同时为空
if (t1 == null || t2 == null || t1.val != t2.val){
return;
}
isSame(t1.left, t2.left);
isSame(t1.right, t2.right);
}
}
答案
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean checkSubTree(TreeNode t1, TreeNode t2) {
if(t2 == null){ // 子树为空
return true;
}
if(t1 == null && t2 != null){ // 子树不为空
return false;
}
// 同时也使用分治法,同样检查t1的左右子树的子树是否包含t2
return isSame(t1, t2) || checkSubTree(t1.left, t2) || checkSubTree(t1.right, t2);
}
public boolean isSame(TreeNode t1, TreeNode t2) {
// if (t1 == t2) {
// return true;
// }
// 同时为空
if (t1 == null && t2 == null) {
return true;
}
// 不同时为空
if (t1 == null || t2 == null){
return false;
}
return t1.val == t2.val && isSame(t1.left, t2.left) && isSame(t1.right, t2.right);
}
}
面试题 04.01. 节点间通路
节点间通路。给定有向图,设计一个算法,找出两个节点之间是否存在一条路径。
示例1:
输入:n = 3, graph = [[0, 1], [0, 2], [1, 2], [1, 2]], start = 0, target = 2
输出:true
示例2:
输入:n = 5, graph = [[0, 1], [0, 2], [0, 4], [0, 4], [0, 1], [1, 3], [1, 4], [1, 3], [2, 3], [3, 4]], start = 0, target = 4
输出 true
答案一:从前往后
因为测试用例start的路径太多了,所以导致从start开始会超时
class Solution {
boolean flag = false;
int[][] graph;
public boolean findWhetherExistsPath(int n, int[][] graph, int start, int target) {
this.graph = graph;
dfs(start, target);
return flag;
}
public void dfs(int start, int target) {
if (flag || start == target) {
flag = true;
return;
}
for (int i = 0; i < graph.length; i++) {
if (graph[i][0] == start) {
int temp = graph[i][0];
// 访问此节点
graph[i][0] = -1;
dfs(graph[i][1], target);
graph[i][0] = temp;
}
}
}
}
答案二:从后往前
测试用例中target的路径比较少,所以不会超时。
class Solution {
boolean flag;
boolean[] used;
public boolean findWhetherExistsPath(int n, int[][] graph, int start, int target) {
used = new boolean[graph.length];
f(n, graph, start, target);
return flag;
}
public void f(int n, int[][] graph, int start, int target) {
if (start == target || flag == true) {
flag = true;
return;
}
// 因为测试用例start的路径太多了,所以导致从start开始会超时
// for (int i = 0; i < graph.length; i++) {
// if (graph[i][0] == start && graph[i][1] == target) {
// flag = true;
// return;
// }
// }
// 所以我换了一种思路,从后往前,从target开始,就不会超时了
for (int i = 0; i < graph.length; i++) {
if (used[i] == false && graph[i][0] == start && graph[i][1] == target) {
flag = true;
return;
}
if (used[i] == false && graph[i][1] == target) {
used[i] = true;
f(n, graph, start, graph[i][0]);
used[i] = false;
}
}
}
}
答案二:从后往前另一种实现
class Solution {
private boolean[] visited = null;
public boolean findWhetherExistsPath(int n, int[][] graph, int start, int target) {
this.visited = new boolean[graph.length];
return helper(graph, start, target);
}
private boolean helper(int[][] graph, int start, int target) {
for (int i = 0; i < graph.length; ++i) {
if (!visited[i]) {
if (graph[i][0] == start && graph[i][1] == target) {
return true;
}
visited[i] = true;
if (graph[i][1] == target && helper(graph, start, graph[i][0])) {
return true;
}
visited[i] = false;
}
}
return false;
}
}
130. 被围绕的区域
给你一个 m x n 的矩阵 board ,由若干字符 'X' 和 'O' ,找到所有被 'X' 围绕的区域,并将这些区域里所有的 'O' 用 'X' 填充。
示例 1:
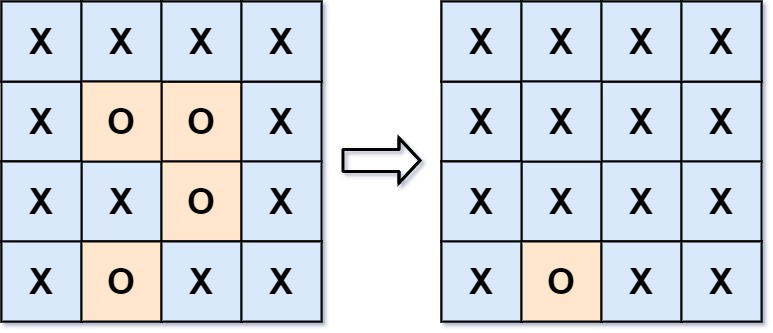
输入:board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]]
输出:[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]]
解释:被围绕的区间不会存在于边界上,换句话说,任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上,或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻,则称它们是“相连”的。
示例 2:
输入:board = [["X"]]
输出:[["X"]]
我的错误答案
我的想法是深度遍历所有O节点,将节点设为X,然后一遇到边界,就还原节点为O。
class Solution {
boolean flag = false;
char[][] board;
public void solve(char[][] board) {
this.board = board;
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
if (board[i][j] == 'O') {
flag = false;
dfs(i, j);
}
}
}
}
public void dfs(int x, int y) {
if (board[x][y] != 'O') {
return;
}
if (flag || x <= 0 || x >= board.length - 1 || y <= 0 || y >= board[x].length - 1) {
flag = true; // 还原
return;
}
board[x][y] = 'X';
dfs(x, y + 1);
dfs(x + 1, y);
dfs(x, y - 1);
dfs(x - 1, y);
if (flag) {
board[x][y] = 'O';
}
}
}
错误的思路点在于,一遇到边界后,向后递归还原只能还原该路径下的O,不属于该路径下的就没法还原,只能通过部分用例。
输入:
[["O","O","O","O","X","X"],["O","O","O","O","O","O"],["O","X","O","X","O","O"],["O","X","O","O","X","O"],["O","X","O","X","O","O"],["O","X","O","O","O","O"]]
输出:
[["O","O","O","O","X","X"],["O","O","O","O","O","O"],["O","X","O","X","O","O"],["O","X","O","X","X","O"],["O","X","O","X","O","O"],["O","X","O","O","O","O"]]
预期结果:
[["O","O","O","O","X","X"],["O","O","O","O","O","O"],["O","X","O","X","O","O"],["O","X","O","O","X","O"],["O","X","O","X","O","O"],["O","X","O","O","O","O"]]
答案
本题给定的矩阵中有三种元素:
- 字母 X;
- 被字母 X 包围的字母 O;
- 没有被字母 X 包围的字母 O。
本题要求将所有被字母 X 包围的字母 O都变为字母 X ,但很难判断哪些 O 是被包围的,哪些 O 不是被包围的。
注意到题目解释中提到:任何边界上的 O 都不会被填充为 X。 我们可以想到,所有的不被包围的 O 都直接或间接与边界上的 O 相连。我们可以利用这个性质判断 O 是否在边界上,具体地说:
- 对于每一个边界上的 O,我们以它为起点,标记所有与它直接或间接相连的字母 O;
- 最后我们遍历这个矩阵,对于每一个字母:
- 如果该字母被标记过,则该字母为没有被字母 X 包围的字母 O,我们将其还原为字母 O;
- 如果该字母没有被标记过,则该字母为被字母 X 包围的字母 O,我们将其修改为字母 X。
方法一:深度优先搜索
思路及解法
我们可以使用深度优先搜索实现标记操作。在下面的代码中,我们把标记过的字母 O 修改为字母 A。
代码
class Solution {
int n, m;
public void solve(char[][] board) {
n = board.length;
if (n == 0) {
return;
}
m = board[0].length;
// 左右边界
for (int i = 0; i < n; i++) {
dfs(board, i, 0);
dfs(board, i, m - 1);
}
// 上下边界
for (int i = 1; i < m - 1; i++) {
dfs(board, 0, i);
dfs(board, n - 1, i);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'A') {
board[i][j] = 'O';
} else if (board[i][j] == 'O') {
board[i][j] = 'X';
}
}
}
}
public void dfs(char[][] board, int x, int y) {
if (x < 0 || x >= n || y < 0 || y >= m || board[x][y] != 'O') {
return;
}
board[x][y] = 'A';
dfs(board, x + 1, y);
dfs(board, x - 1, y);
dfs(board, x, y + 1);
dfs(board, x, y - 1);
}
}
复杂度分析
-
时间复杂度:\(O(n \times m)\),其中 n 和 m 分别为矩阵的行数和列数。深度优先搜索过程中,每一个点至多只会被标记一次。
-
空间复杂度:\(O(n \times m)\),其中 n 和 m 分别为矩阵的行数和列数。主要为深度优先搜索的栈的开销。
剪枝实例
93. 复原 IP 地址
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 '.' 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。
给定一个只包含数字的字符串 s ,用以表示一个 IP 地址,返回所有可能的有效 IP 地址,这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。
示例 1:
输入:s = "25525511135"
输出:["255.255.11.135","255.255.111.35"]
示例 2:
输入:s = "0000"
输出:["0.0.0.0"]
示例 3:
输入:s = "101023"
输出:["1.0.10.23","1.0.102.3","10.1.0.23","10.10.2.3","101.0.2.3"]
我的
class Solution {
String s;
List<String> list = new ArrayList<>();
StringBuilder sb = new StringBuilder();
public List<String> restoreIpAddresses(String s) {
this.s = s;
dfs(0, 1);
return list;
}
public void dfs(int index, int seg) {
if (index >= s.length() && seg > 4) {
list.add(sb.toString());
return;
}
if (index >= s.length() || seg > 4) {
return;
}
// 由于不能有前导零,如果当前数字为 0,那么这一段 IP 地址只能为 0
if (s.charAt(index) == '0') {
sb.append(0);
if (seg < 4) {
sb.append(".");
}
dfs(index + 1, seg + 1);
if (seg < 4) {
sb.deleteCharAt(sb.length() - 1);
}
sb.deleteCharAt(sb.length() - 1);
return;
}
for (int i = 1; i <= 3; i++) {
if (index + i > s.length()) {
break;
}
// String num = s.substring(index, index + i);
// if (num.compareTo("0") >= 0 && num.compareTo("255") <= 0) {
int num = Integer.valueOf(s.substring(index, index + i));
if (num >= 0 && num <= 255) {
sb.append(num);
if (seg < 4) {
sb.append(".");
}
dfs(index + i, seg + 1);
if (seg < 4) {
sb.deleteCharAt(sb.length() - 1);
}
sb.delete(sb.length() - i, sb.length());
}
}
}
}
笔者将不定期更新【考研或就业】的专业相关知识以及自身理解,希望大家能【关注】我。
如果觉得对您有用,请点击左下角的【点赞】按钮,给我一些鼓励,谢谢!
如果有更好的理解或建议,请在【评论】中写出,我会及时修改,谢谢啦!
本文来自博客园,作者:Nemo&
转载请注明原文链接:https://www.cnblogs.com/blknemo/p/12431911.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号