【数据结构】栈与队列
栈和队列
我们以下的使用的栈或队列都是作为一个工具来解决其他问题的,我们可以把栈或队列的声明和操作写的很简单,而不必分函数写出。
栈:Stack
队列:Queue
栈和队列:Deque(double ended queue, 双端队列)(万能)
在Java Doc里建议使用Deque接口替代Stack完成栈的功能,为什么呢?
因为Stack是继承Vector,Vector是由数组实现线程安全(方法使用synchronized修饰)的集合类,它包含了大量集合处理的方法,而Stack复用了Vector的方法实现进栈和出栈的操作,基于数组实现相比于链表实现,效率上受影响。同时,因为继承Vector类,Stack可以复用Vector的方法,这是Stack设计不严谨的地方
// 双端队列
Deque<Integer> deque = new LinkedList<Integer>();
deque.offer();
deque.offerFirst();
deque.offerLast();
deque.poll();
deque.pollFirst();
deque.pollLast();
deque.peek();
deque.peekFirst();
deque.peekLast();
// 栈
Deque<Integer> stack = new LinkedList<Integer>();
stack.push(); // deque.addFirst();
stack.pop(); // deque.removeFirst();
stack.peek(); // deque.peekFirst();
// 队列
Deque<Integer> queue = new LinkedList<Integer>();
queue.offer(); // deque.offerLast();
queue.poll(); // deque.pollFirst();
queue.peek(); // deque.peekFirst();
队列:
| Queue Method | Equivalent Deque Method | 说明 |
|---|---|---|
add(e) |
addLast(e) |
向队尾插入元素,失败则抛出异常 |
offer(e) |
offerLast(e) |
向队尾插入元素,失败则返回false |
remove() |
removeFirst() |
获取并删除队首元素,失败则抛出异常 |
poll() |
pollFirst() |
获取并删除队首元素,失败则返回null |
element() |
getFirst() |
获取但不删除队首元素,失败则抛出异常 |
peek() |
peekFirst() |
获取但不删除队首元素,失败则返回null |
栈:需要注意,栈的操作都是针对头节点的,而不是尾结点。
所以使用双端队列的时候最好带上First或Last。
| Stack Method | Equivalent Deque Method | 说明 |
|---|---|---|
push(e) |
addFirst(e) |
向栈顶插入元素,失败则抛出异常 |
| 无 | offerFirst(e) |
向栈顶插入元素,失败则返回false |
pop() |
removeFirst() |
获取并删除栈顶元素,失败则抛出异常 |
| 无 | pollFirst() |
获取并删除栈顶元素,失败则返回null |
peek() |
getFirst() |
获取但不删除栈顶元素,失败则抛出异常 |
| 无 | peekFirst() |
获取但不删除栈顶元素,失败则返回null |
顺序栈
-
声明一个栈并初始化:
ElemType stack[maxSize]; //存放栈中的元素 int top = -1; //栈顶指针(指向栈顶元素) -
元素进栈:
stack[++top] = x; -
元素出栈:
x = stack[top--]; -
判断栈空:
top == -1; //栈空 top > -1; //栈非空
顺序队列
-
声明一个队列并初始化:
ElemType queue[maxSize]; //存放队列中元素 int front = -1, rear = -1; //队头(指向队头元素的前一个位置),队尾(指向队尾元素) -
元素入队:
queue[++rear] = x; -
元素出队:
x = queue[++front]; -
判断队空:
front == rear; //队空 front < rear; //队非空
- 使用“栈”遍历:是用来从最近访问的一个结点开始,访问其他结点
- 使用“队列”遍历:是用来按照访问的顺序开始,访问其他结点
栈
卡特兰(Catalan)数:\({{1}\over{n+1}}C_{2n}^{n}\)
应用:对于n个不同元素进栈,出栈序列的个数为\({{1}\over{n+1}}C_{2n}^{n}\)
-
栈的应用:括号匹配、表达式求值(后缀表达式)、递归、迷宫求解等。
-
以元素。。开头的序列个数是,把该元素出栈,再将剩下的元素一个个插到现有栈中元素之间,即可算出个数。
顺序栈
-
基本概念:
采用顺序存储的栈称为顺序栈,它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素,同时附设一个指针(top)指向当前栈顶的位置。 -
存储结构:
#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
ElemType data[MaxSize]; //存放栈中元素
int top; //栈顶指针
}SqStack; //Sequence Stack
- 基本操作:
- 栈顶指针:S.top,初始时设置
S.top=-1;(即 指向了栈顶元素) - 栈顶元素:
S.data[S.top]; - 进栈操作:栈不满是,栈顶指针先加1,再送值到栈顶元素;
- 出栈操作:栈非空时,先取栈顶元素值,再将栈顶指针减1;
- 栈空条件:
S.top == -1; - 栈满条件:
S.top == MaxSize-1; - 栈长:
S.top+1
- 栈顶指针:S.top,初始时设置
共享栈
-
基本概念:
利用栈底位置相对不变的特性,可让两个顺序栈共享一个一维数据空间,将两个站的栈底分别设置在共享空间的两端,两个栈顶向共享空间的中间延伸。 -
基本操作:
-
栈空条件:
- 0号栈:
top0 = -1 - 1号栈:
top1 = MaxSize
- 0号栈:
-
栈满条件:
top1 - top0 = 1(即 当两个栈顶指针相邻时栈满) -
进栈操作:
- 0号栈:top0先加1再赋值
- 1号栈:top1先减1再赋值
-
出栈操作:栈非空时,
- 0号栈:先取栈顶元素值,再将top0减1;
- 1号栈:先取栈顶元素值,再将top1加1
-
链栈
在表头入栈出栈
-
基本概念:
采用链式存储的栈称为链栈,通常采用单链表实现,并规定所有操作都是在单链表的表头进行的。 -
存储结构:
typedef struct LinkNode {
ElemType data; //数据域
struct LinkNode *next; //指针域
}*LiStack; //List Stack
- 操作:
//插入x结点
x->next = top;
top = x;
- 优点:
便于多个栈共享存储空间和提高其效率,且不存在栈满上溢的情况。便于结点的插入与删除。
队列
- 队列的应用:层次遍历、解决主机与外部设备之间速度不匹配的问题、解决由多用户引起的资源竞争的问题、页面替换算法等。
顺序:先头后尾、左头右尾(头尾)
顺序队列
-
基本概念:
队列的顺序实现是指分配一块连续的存储单元存放队列中的元素,并附设两个指针front和rear分别指向队头元素和队尾元素的位置。(这里队头指针指向队头元素的前一个位置,队尾指针指向队尾元素)(避免队空与队列中只有一个元素时无法区分) -
存储结构:
#define MaxSize 50 //定义栈中元素的最大个数
typedef struct {
ElemType data[MaxSize]; //存放队列元素
int front, rear; //队头指针和队尾指针
}SqQueue; //Sequence Queue
- 基本操作:
- 初始状态;Q.front = -1; Q.rear = -1;
- 队空条件:Q.front == Q.rear; (因为队头指针指向队头元素的前一个位置,所以当与队尾指针相等时,队空)
- 进队操作:队不满时,先送值到队尾元素,再将队尾指针加1;
- 出队操作:队不空时,先取队头元素值,再将队头指针加1;
队满条件:无法判断队满,当rear > maxsize-1,front > -1时,其实队中依然有空位(front之前还有空位)可以存放元素,只是由于被指针欺骗了,这种现象称为“假溢出”。
循环队列
-
基本概念:
将顺序队列臆造为一个环状的空间,即吧存储队列元素的表从逻辑上视为一个环,称为循环队列。当队首指针Q.front=MaxSize-1后,再前进一个位置就自动到0,利用取余运算(%)。 -
基本操作:
- 初始时:Q.front = Q.rear = 0;
- 入队操作:Q.rear = (Q.rear+1)%MaxSize; (在队尾排队)
- 出队操作:Q.front = (Q.front+1)%MaxSize; (在队头出队)
- 队列长度:(Q.rear+MaxSize-Q.front)%MaxSize。
- 出队入队时:指针都按顺时针方向进1
但是无法区分队空与队满(都为Q.front == Q.rear)
为了区分队空队满的情况,有三种处理方式:
-
牺牲一个单元来区分队空队满,入队时少用一个队列单元。约定以“队头指针在队尾指针的下一位置作为队满的标志”
- 队满条件:(Q.rear+1)%MaxSize == Q.front;
- 队空条件:Q.front == Q.rear;
- 队列中元素的个数:(Q.rear-Q.front+MaxSize)%MaxSize。
-
类型中增设表示元素个数的数据成员。
- 队空条件:Q.size == 0;
- 队满条件:Q.size == MaxSize。
这两种情况都有Q.front == Q.rear。
-
类型中增设tag数据成员,以区分是队满还是队空。
- 队空条件:tag == 0时,若因删除导致Q.front == Q.rear,则为队空;
- 队满条件:tag == 1时,若因插入导致Q.front == Q.rear,则为队满。
链队列
头出尾进
-
基本概念:
队列的链式表示称为链队列,它实际上是一个同时带有队头指针和队尾指针的单链表(通常设计成带头结点的单链表,方便操作)。头指针指向队头结点,尾指针指向队尾结点,即单链表的最后一个结点(注意与顺序队列不同)。 -
存储结构:
typedef struct LinkNode{//链式队列结点
ElemType data;
struct LinkNode *next;
}LinkNode;
typedef struct { //链式队列
LinkNode *front, *rear; //队列的队头和队尾指针
}LinkQueue;
-
基本操作:
- 初始化:
Q.front = Q.rear = 头结点; - 队空条件:
Q.front == NULL && Q.rear == NULL; - 入队操作:尾插法;
- 出队操作:删除头。
- 初始化:
-
适用性:
链队列特别适合于数据元素变动比较大的情形,而且不存在队列满且产生溢出的问题。
另外,假如程序中要使用多个队列,与多个栈的情形一样,最好使用链队列,这样就不会出现存储分配不合理和“溢出”的问题。
双端队列
受限的唯一一端,最好放在左边,无论是输出还是输出,好看一些。
- 基本概念:
双端队列是指允许两端都可以进行入队和出队操作的队列。 - 受限的双端队列:
- 输出受限:****只有一端能输出,两端都能输入
- 输入受限:****只有一端能输入,两端都能输出
- 技巧:
- 对于这种受限的双端队列,左右仅此一个的操作,为解题关键。
- 输入受限:只有一端能进行输入操作,输入操作唯一
∵入队序列唯一
∴看能否出成选项当中的序列 - 输出受限:只有一端能进行输出操作,输出操作唯一
∵出队序列唯一
∴看能否入成这种队列
栈的相关算法
栈的一般思路:
for (int i = 0; i < nums.length; i++) {
if (入栈条件) {
stack.push(nums[i]);
} else { // 否则,出栈
stack.pop();
}
}
剑指 Offer 09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:
输入:
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出:[null,null,3,-1]
示例 2:
输入:
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出:[null,-1,null,null,5,2]
答案
方法一:双栈:将栈逆置
思路和算法
维护两个栈,第一个栈支持插入操作,第二个栈支持删除操作。
根据栈先进后出的特性,我们每次往第一个栈里插入元素后,第一个栈的底部元素是最后插入的元素,第一个栈的顶部元素是下一个待删除的元素。为了维护队列先进先出的特性,我们引入第二个栈,用第二个栈维护待删除的元素,在执行删除操作的时候我们首先看下第二个栈是否为空。如果为空,我们将第一个栈里的元素一个个弹出插入到第二个栈里,这样第二个栈里元素的顺序就是待删除的元素的顺序,要执行删除操作的时候我们直接弹出第二个栈的元素返回即可。
成员变量
- 维护两个栈 stack1 和 stack2,其中 stack1 支持插入操作,stack2 支持删除操作
构造方法
- 初始化 stack1 和 stack2 为空
插入元素
插入元素对应方法 appendTail
- stack1 直接插入元素
删除元素
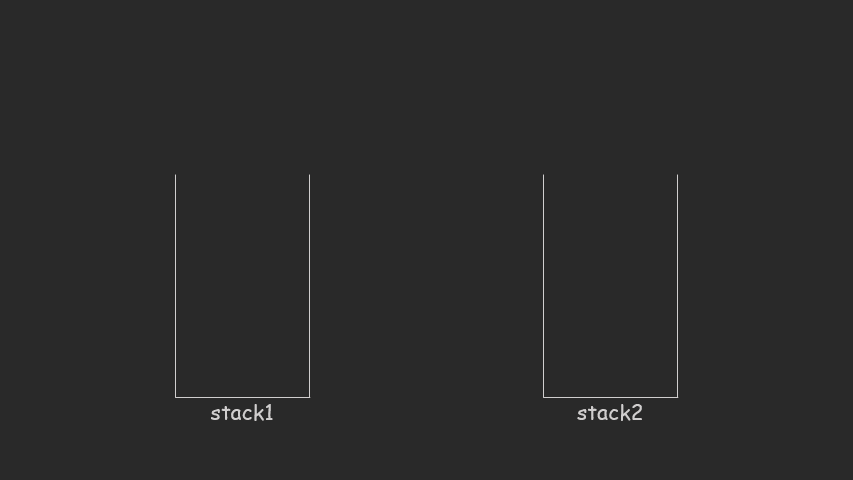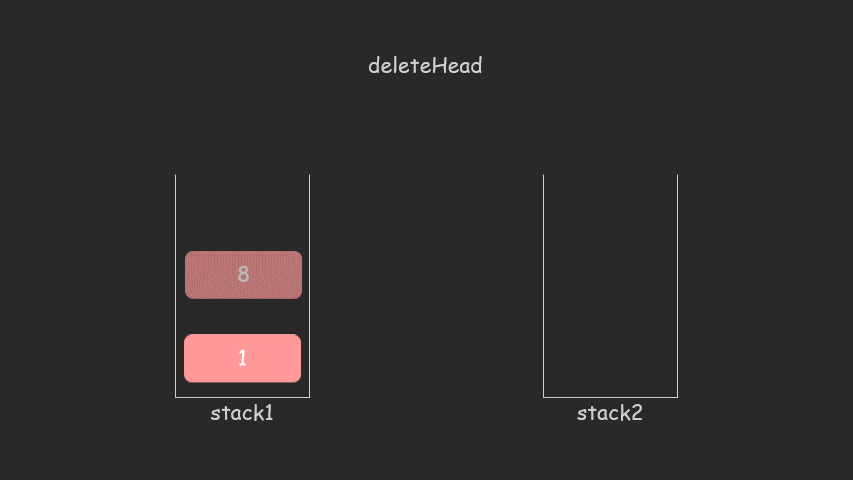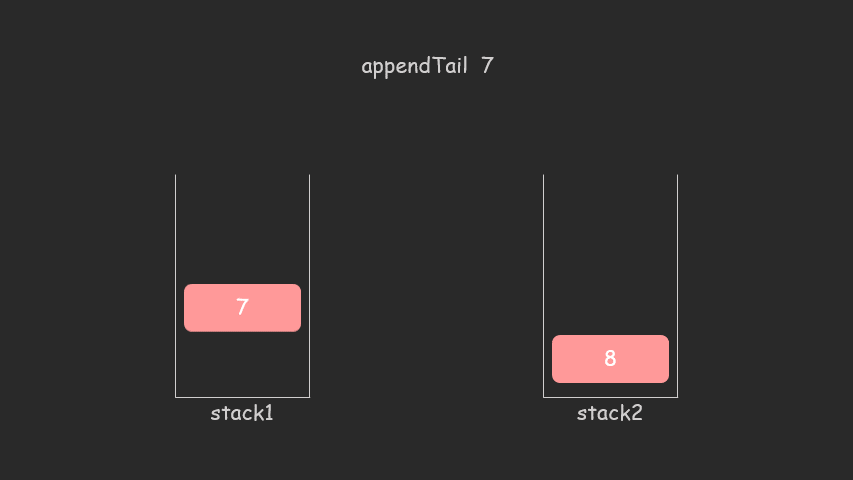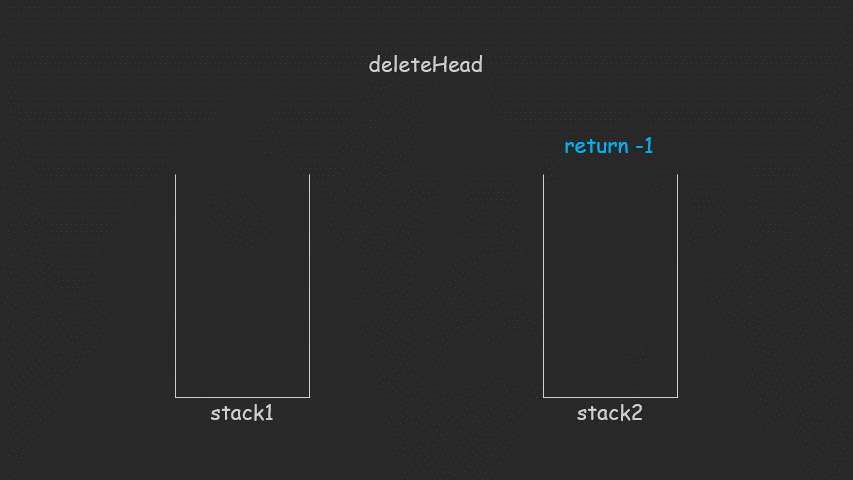
删除元素对应方法 deleteHead
- 如果 stack2 为空,则将 stack1 里的所有元素弹出插入到 stack2 里
- 如果 stack2 仍为空,则返回 -1,否则从 stack2 弹出一个元素并返回
class CQueue {
Deque<Integer> stack1;
Deque<Integer> stack2;
public CQueue() {
stack1 = new LinkedList<Integer>();
stack2 = new LinkedList<Integer>();
}
public void appendTail(int value) {
stack1.push(value);
}
public int deleteHead() {
// 如果第二个栈为空
if (stack2.isEmpty()) {
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
if (stack2.isEmpty()) {
return -1;
} else {
int deleteItem = stack2.pop();
return deleteItem;
}
}
}
复杂度分析
-
时间复杂度:对于插入和删除操作,时间复杂度均为 \(O(1)\)。插入不多说,对于删除操作,虽然看起来是 \(O(n)\) 的时间复杂度,但是仔细考虑下每个元素只会「至多被插入和弹出 stack2 一次」,因此均摊下来每个元素被删除的时间复杂度仍为 \(O(1)\)。
-
空间复杂度:\(O(n)\)。需要使用两个栈存储已有的元素。
我的答案:
class CQueue {
Stack<Integer> s1;
Stack<Integer> s2;
public CQueue() {
s1 = new Stack<>();
s2 = new Stack<>();
}
public void appendTail(int value) {
s1.push(value);
}
public int deleteHead() {
if (s2.isEmpty()) {
while (!s1.isEmpty()) {
s2.push(s1.pop());
}
}
if (s2.isEmpty()) {
return -1;
} else {
return s2.pop();
}
}
}
/**
* Your CQueue object will be instantiated and called as such:
* CQueue obj = new CQueue();
* obj.appendTail(value);
* int param_2 = obj.deleteHead();
*/
操作栈
其实,操作栈可以视为一种优先级的单调栈,既然是优先级单调栈,那么自然是优先级单调递增栈。
左括号优先级高于右括号,所以一遇到右括号就需要将左括号弹出进行匹配。
适用场景:适用于此元素当前不能处理,需要临时存放,直到达到某条件后才能取出来进行处理的情况。
如 括号匹配
操作栈分为两部分:将不同类型的元素使用操作栈分别存放,如 (操作数、操作符)、(不可变符号、可变符号)
- 操作数栈:存放待操作的数字元素,如 1、2;
技巧:有时候我们可以存放待操作元素的下标,来记录其位置,以便于需要操作时能够找到对应的元素位置。
- 操作符栈:存放待操作的操作符元素,如 加法(+)
算法思路:
- 遍历元素,将操作数元素临时存入栈中
- 直到当前操作元素匹配某种条件后(如 右括号),开始取出操作数栈内的操作数元素 和 操作栈内的操作元素,进行处理,合并为新的操作数元素,继续存入操作数栈中。
括号匹配的两次遍历通用思路:
- 有效括号:(左括号数=右括号数)****所有左括号的右边都有与之相匹配的右括号(
左括号数>=右括号数),并且 所有右括号的左边也都有与之相匹配的左括号(右括号数>=左括号数)。 - 顺序遍历:证明所有不可变右括号的左边都有与之相对应的左括号或可变括号相匹配;
- 逆序遍历:证明所有不可变左括号的右边都有与之相对应的右括号或可变括号相匹配。
1614. 括号的最大嵌套深度
如果字符串满足以下条件之一,则可以称之为 有效括号字符串(valid parentheses string,可以简写为 VPS):
- 字符串是一个空字符串 "",或者是一个不为 "(" 或 ")" 的单字符。
- 字符串可以写为 AB(A 与 B 字符串连接),其中 A 和 B 都是 有效括号字符串 。
- 字符串可以写为 (A),其中 A 是一个 有效括号字符串 。
类似地,可以定义任何有效括号字符串 S 的 嵌套深度 depth(S):
- depth("") = 0
- depth(C) = 0,其中 C 是单个字符的字符串,且该字符不是 "(" 或者 ")"
- depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是 有效括号字符串
- depth("(" + A + ")") = 1 + depth(A),其中 A 是一个 有效括号字符串
例如:""、"()()"、"()(()())" 都是 有效括号字符串(嵌套深度分别为 0、1、2),而 ")(" 、"(()" 都不是 有效括号字符串 。
给你一个 有效括号字符串 s,返回该字符串的 s 嵌套深度 。
示例 1:
输入:s = "(1+(2*3)+((8)/4))+1"
输出:3
解释:数字 8 在嵌套的 3 层括号中。
示例 2:
输入:s = "(1)+((2))+(((3)))"
输出:3
答案
对于括号计算类题目,我们往往可以用栈来思考。
遍历字符串 s,如果遇到了一个左括号,那么就将其入栈;如果遇到了一个右括号,那么就弹出栈顶的左括号,与该右括号匹配。这一过程中的栈的大小的最大值,即为 s 的嵌套深度。
代码实现时,由于我们只需要考虑栈的大小,我们可以用一个变量 \(\textit{size}\) 表示栈的大小,当遇到左括号时就将其加一,遇到右括号时就将其减一,从而表示栈中元素的变化。这一过程中 \(\textit{size}\) 的最大值即为 s 的嵌套深度。
class Solution {
public int maxDepth(String s) {
int ans = 0, size = 0;
for (int i = 0; i < s.length(); ++i) {
char ch = s.charAt(i);
if (ch == '(') {
++size;
ans = Math.max(ans, size);
} else if (ch == ')') {
--size;
}
}
return ans;
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是字符串 \(\textit{s}\) 的长度。
- 空间复杂度:\(O(1)\)。我们只需要常数空间来存放若干变量。
我的
class Solution {
public int maxDepth(String s) {
Stack<Character> stack = new Stack<>();
int max = 0;
char[] chars = s.toCharArray();
for (char c : chars) {
if (c == '(') {
stack.push(c);
} else if (c == ')') {
stack.pop();
}
max = Math.max(max, stack.size());
}
return max;
}
}
1021. 删除最外层的括号
有效括号字符串为空 ""、"(" + A + ")" 或 A + B ,其中 A 和 B 都是有效的括号字符串,+ 代表字符串的连接。
例如,"","()","(())()" 和 "(()(()))" 都是有效的括号字符串。
如果有效字符串 s 非空,且不存在将其拆分为 s = A + B 的方法,我们称其为原语(primitive),其中 A 和 B 都是非空有效括号字符串。
给出一个非空有效字符串 s,考虑将其进行原语化分解,使得:s = P_1 + P_2 + ... + P_k,其中 P_i 是有效括号字符串原语。
对 s 进行原语化分解,删除分解中每个原语字符串的最外层括号,返回 s 。
示例 1:
输入:s = "(()())(())"
输出:"()()()"
解释:
输入字符串为 "(()())(())",原语化分解得到 "(()())" + "(())",
删除每个部分中的最外层括号后得到 "()()" + "()" = "()()()"。
示例 2:
输入:s = "(()())(())(()(()))"
输出:"()()()()(())"
解释:
输入字符串为 "(()())(())(()(()))",原语化分解得到 "(()())" + "(())" + "(()(()))",
删除每个部分中的最外层括号后得到 "()()" + "()" + "()(())" = "()()()()(())"。
示例 3:
输入:s = "()()"
输出:""
解释:
输入字符串为 "()()",原语化分解得到 "()" + "()",
删除每个部分中的最外层括号后得到 "" + "" = ""。
答案
思路
遍历 s,并用一个栈来表示括号的深度。遇到 \(\text{‘(’}\) 则将字符入栈,遇到 \(\text{‘)’}\) 则将栈顶字符出栈。栈从空到下一次空的过程,则是扫描了一个原语的过程。一个原语中,首字符和尾字符应该舍去,其他字符需放入结果字符串中。因此,在遇到 \(\text{‘(’}\) 并将字符入栈后,如果栈的深度为 1,则不把字符放入结果;在遇到 \(\text{‘)’}\) 并将栈顶字符出栈后,如果栈为空,则不把字符放入结果。其他情况下,需要把字符放入结果。代码对流程进行了部分优化,减少了判断语句。
class Solution {
public String removeOuterParentheses(String s) {
char[] chars = s.toCharArray();
StringBuilder sb = new StringBuilder();
Stack<Character> stack = new Stack<>();
for (char c : chars) {
// 先出栈
if (c == ')') {
stack.pop();
}
// 空栈状态到第一个入栈的元素 和 最后一个元素出栈到空栈状态 均不加入结果
if (!stack.isEmpty()) {
sb.append(c);
}
if (c == '(') {
stack.push('(');
}
}
return sb.toString();
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是输入 s 的长度。仅需遍历 s 一次。
-
空间复杂度:\(O(n)\),其中 n 是输入 s 的长度。需要使用栈,长度最大为 \(O(n)\)。
1111. 有效括号的嵌套深度
有效括号字符串 定义:对于每个左括号,都能找到与之对应的右括号,反之亦然。详情参见题末「有效括号字符串」部分。
嵌套深度 depth 定义:即有效括号字符串嵌套的层数,depth(A) 表示有效括号字符串 A 的嵌套深度。详情参见题末「嵌套深度」部分。
有效括号字符串类型与对应的嵌套深度计算方法如下图所示:
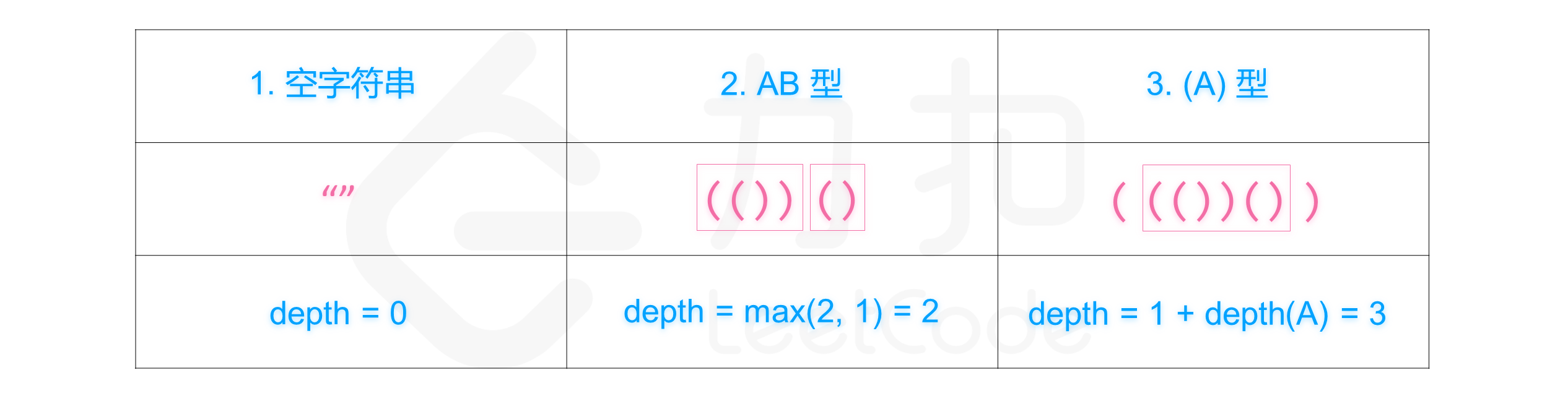
给你一个「有效括号字符串」 seq,请你将其分成两个不相交的有效括号字符串,A 和 B,并使这两个字符串的深度最小。
- 不相交:每个 seq[i] 只能分给 A 和 B 二者中的一个,不能既属于 A 也属于 B 。
- A 或 B 中的元素在原字符串中可以不连续。
- A.length + B.length = seq.length
- 深度最小:max(depth(A), depth(B)) 的可能取值最小。
划分方案用一个长度为 seq.length 的答案数组 answer 表示,编码规则如下:
- answer[i] = 0,seq[i] 分给 A 。
- answer[i] = 1,seq[i] 分给 B 。
- 如果存在多个满足要求的答案,只需返回其中任意 一个 即可。
示例 1:
输入:seq = "(()())"
输出:[0,1,1,1,1,0]
示例 2:
输入:seq = "()(())()"
输出:[0,0,0,1,1,0,1,1]
解释:本示例答案不唯一。
按此输出 A = "()()", B = "()()", max(depth(A), depth(B)) = 1,它们的深度最小。
像 [1,1,1,0,0,1,1,1],也是正确结果,其中 A = "()()()", B = "()", max(depth(A), depth(B)) = 1 。
我的
注意:我的做法只是为了示意此题用栈,其实这块操作栈存下来的待操作的元素都没什么实际的作用,有用的只有栈的大小,可以换成数字来直接计数,更加节省性能。
class Solution {
public int[] maxDepthAfterSplit(String seq) {
Stack<Character> stack = new Stack<>();
char[] chars = seq.toCharArray();
int[] res = new int[chars.length];
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '(') {
stack.push(chars[i]);
// 奇数深度进入B,偶数深度进入A
res[i] = stack.size() % 2;
} else {
res[i] = stack.size() % 2;
stack.pop();
}
}
return res;
}
}
答案
思路及算法
要求划分出使得最大嵌套深度最小的分组,我们首先得知道如何计算嵌套深度。我们可以通过栈实现括号匹配来计算:
维护一个栈 s,从左至右遍历括号字符串中的每一个字符:
- 如果当前字符是 (,就把 ( 压入栈中,此时这个 ( 的嵌套深度为栈的高度;
- 如果当前字符是 ),此时这个 ) 的嵌套深度为栈的高度,随后再从栈中弹出一个 (。
下面给出了括号序列 (()(())()) 在每一个字符处的嵌套深度:
括号序列 ( ( ) ( ( ) ) ( ) )
下标编号 0 1 2 3 4 5 6 7 8 9
嵌套深度 1 2 2 2 3 3 2 2 2 1
知道如何计算嵌套深度,问题就很简单了:只要在遍历过程中,我们保证栈内一半的括号属于序列 A,一半的括号属于序列 B,那么就能保证拆分后最大的嵌套深度最小,是当前最大嵌套深度的一半。要实现这样的对半分配,我们只需要把奇数层的 ( 分配给 A,偶数层的 ( 分配给 B 即可。对于上面的例子,我们将嵌套深度为 1 和 3 的所有括号 (()) 分配给 A,嵌套深度为 2 的所有括号 ()()() 分配给 B。
此外,由于在这个问题中,栈中只会存放 (,因此我们不需要维护一个真正的栈,只需要用一个变量模拟记录栈的大小。
class Solution {
public int[] maxDepthAfterSplit(String seq) {
int d = 0;
int length = seq.length();
int[] ans = new int[length];
for (int i = 0; i < length; i++) {
if (seq.charAt(i) == '(') {
++d;
ans[i] = d % 2;
} else {
ans[i] = d % 2;
--d;
}
}
return ans;
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 为字符串的长度。我们只需要遍历括号字符串一次。
- 空间复杂度:\(O(1)\)。除答案数组外,我们只需要常数个变量。
20. 有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
示例 1:
输入:s = "()"
输出:true
示例 2:
输入:s = "()[]{}"
输出:true
示例 3:
输入:s = "(]"
输出:false
示例 4:
输入:s = "([)]"
输出:false
示例 5:
输入:s = "{[]}"
输出:true
我的
class Solution {
public boolean isValid(String s) {
Deque<Character> stack = new LinkedList<>();
for (int i = 0; i < s.length(); i++) {
char cur = s.charAt(i);
if (cur == '(' || cur == '[' || cur == '{') {
stack.push(cur);
} else {
if (!stack.isEmpty() && ((cur == ')' && stack.peek() == '(')
|| (cur == ']' && stack.peek() == '[')
|| (cur == '}' && stack.peek() == '{'))) {
stack.pop();
} else {
return false;
}
}
}
return stack.isEmpty();
}
}
答案
方法一:栈
判断括号的有效性可以使用「栈」这一数据结构来解决。
我们遍历给定的字符串 s。当我们遇到一个左括号时,我们会期望在后续的遍历中,有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合,因此我们可以将这个左括号放入栈顶。
当我们遇到一个右括号时,我们需要将一个相同类型的左括号闭合。此时,我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型,或者栈中并没有左括号,那么字符串 s 无效,返回 \(\text{False}\)。为了快速判断括号的类型,我们可以使用哈希表存储每一种括号。哈希表的键为右括号,值为相同类型的左括号。
在遍历结束后,如果栈中没有左括号,说明我们将字符串 s 中的所有左括号闭合,返回 \(\text{True}\),否则返回 \(\text{False}\)。
注意到有效字符串的长度一定为偶数,因此如果字符串的长度为奇数,我们可以直接返回 \(\text{False}\),省去后续的遍历判断过程。
class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
Map<Character, Character> map = new HashMap<>();
map.put(')', '(');
map.put(']', '[');
map.put('}', '{');
char[] chars = s.toCharArray();
for (char c : chars) {
if (map.containsValue(c)) {
stack.push(c);
} else {
// 只剩下右括号了 或者 右括号与左括号不匹配
if (stack.isEmpty() || map.get(c) != stack.pop()) {
return false;
}
}
}
return stack.isEmpty();
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是字符串 s 的长度。
- 空间复杂度:\(O(n + |\Sigma|)\),其中 \(\Sigma\) 表示字符集,本题中字符串只包含 6 种括号,\(|\Sigma| = 6\)。栈中的字符数量为 \(O(n)\),而哈希表使用的空间为 \(O(|\Sigma|)\),相加即可得到总空间复杂度。
678. 有效的括号字符串
给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则:
- 任何左括号 ( 必须有相应的右括号 )。
- 任何右括号 ) 必须有相应的左括号 ( 。
- 左括号 ( 必须在对应的右括号之前 )。
*可以被视为单个右括号 ) ,或单个左括号 ( ,或一个空字符串。- 一个空字符串也被视为有效字符串。
示例 1:
输入: "()"
输出: True
示例 2:
输入: "(*)"
输出: True
示例 3:
输入: "(*))"
输出: True
常规错误做法
class Solution {
public boolean checkValidString(String s) {
// 存放左括号
Stack<Character> opStack = new Stack<>();
// 存放星号
Stack<Character> strStack = new Stack<>();
char[] chars = s.toCharArray();
// 星号作为左括号使用
for (char c : chars) {
if (c == '(') {
opStack.push(c);
} else if (c == '*') {
strStack.push(c);
} else {
if (!opStack.isEmpty()) {
opStack.pop();
} else if (!strStack.isEmpty()) {
strStack.pop();
} else {
return false;
}
}
}
// 星号作为右括号使用
if (strStack.size() >= opStack.size()) {
return true;
}
return false;
}
}
当用例为*(时,本应该输出false,结果输出了true,是错误的!
我们这时候才反应过来,在星号充当右括号的时候,星号应该在左括号的后面!而不能直接相互抵消,所以我们需要记录括号的下标。
方法一:栈
括号匹配的问题可以用栈求解。
如果字符串中没有星号,则只需要一个栈存储左括号,在从左到右遍历字符串的过程中检查括号是否匹配。
在有星号的情况下,需要两个栈分别存储左括号和星号。从左到右遍历字符串,进行如下操作。
- 如果遇到左括号,则将当前下标存入左括号栈。
- 如果遇到星号,则将当前下标存入星号栈。
- 如果遇到右括号,则需要有一个左括号或星号和右括号匹配,由于星号也可以看成右括号或者空字符串,因此当前的右括号应优先和左括号匹配,没有左括号时和星号匹配:
- 如果左括号栈不为空,则从左括号栈弹出栈顶元素;
- 如果左括号栈为空且星号栈不为空,则从星号栈弹出栈顶元素;
- 如果左括号栈和星号栈都为空,则没有字符可以和当前的右括号匹配,返回 \(\text{false}\)。
遍历结束之后,左括号栈和星号栈可能还有元素。为了将每个左括号匹配,需要将星号看成右括号,且每个左括号必须出现在其匹配的星号之前。当两个栈都不为空时,每次从左括号栈和星号栈分别弹出栈顶元素,对应左括号下标和星号下标,判断是否可以匹配,匹配的条件是左括号下标小于星号下标,如果左括号下标大于星号下标则返回 \(\text{false}\)。
最终判断左括号栈是否为空。如果左括号栈为空,则左括号全部匹配完毕,剩下的星号都可以看成空字符串,此时 s 是有效的括号字符串,返回 \(\text{true}\)。如果左括号栈不为空,则还有左括号无法匹配,此时 s 不是有效的括号字符串,返回 \(\text{false}\)。
class Solution {
public boolean checkValidString(String s) {
// 左括号的栈
Stack<Integer> leftStack = new Stack<Integer>();
// 星号的栈,都用于存放数组下标
Stack<Integer> asteriskStack = new Stack<Integer>();
char[] chars = s.toCharArray();
// 星号作为左括号使用,用来匹配右括号
// 此时充当左括号的星号一定在右括号的左边,无需额外判断下标
for (int i = 0; i < chars.length; i++) {
char c = chars[i];
if (c == '(') {
leftStack.push(i);
} else if (c == '*') {
asteriskStack.push(i);
} else {
if (!leftStack.isEmpty()) {
leftStack.pop();
} else if (!asteriskStack.isEmpty()) {
asteriskStack.pop();
} else {
return false;
}
}
}
// 星号作为右括号使用,用来匹配左括号,但是需要在左括号的后面才能正确匹配
while (!leftStack.isEmpty() && !asteriskStack.isEmpty()) {
int leftIndex = leftStack.pop();
int asteriskIndex = asteriskStack.pop();
// 判断充当右括号的星号算法在左括号后面
if (leftIndex > asteriskIndex) {
return false;
}
}
return leftStack.isEmpty();
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是字符串 s 的长度。需要遍历字符串一次,遍历过程中每个字符的操作时间都是 \(O(1)\),遍历结束之后对左括号栈和星号栈弹出元素的操作次数不会超过 n。
- 空间复杂度:\(O(n)\),其中 n 是字符串 s 的长度。空间复杂度主要取决于左括号栈和星号栈,两个栈的元素总数不会超过 n。
贪心
使用贪心的思想,可以将空间复杂度降到 \(O(1)\)。
从左到右遍历字符串,遍历过程中,未匹配的左括号数量可能会出现如下变化:
- 如果遇到左括号,则未匹配的左括号数量加 1;
- 如果遇到右括号,则需要有一个左括号和右括号匹配,因此未匹配的左括号数量减 1;
- 如果遇到星号,由于星号可以看成左括号、右括号或空字符串,因此未匹配的左括号数量可能加 1、减 1 或不变。
基于上述结论,可以在遍历过程中维护未匹配的左括号数量可能的最小值和最大值,根据遍历到的字符更新最小值和最大值:
- 如果遇到左括号,则将最小值和最大值分别加 1;
- 如果遇到右括号,则将最小值和最大值分别减 1;
- 如果遇到星号,则将最小值减 1,将最大值加 1。
任何情况下,未匹配的左括号数量必须非负,因此当最大值变成负数时,说明没有左括号可以和右括号匹配,返回 \(\text{false}\)。
当最小值为 0 时,不应将最小值继续减少,以确保最小值非负。
遍历结束时,所有的左括号都应和右括号匹配,因此只有当最小值为 0 时,字符串 s 才是有效的括号字符串。
class Solution {
public boolean checkValidString(String s) {
int minCount = 0, maxCount = 0;
int n = s.length();
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c == '(') {
minCount++;
maxCount++;
} else if (c == ')') {
minCount = Math.max(minCount - 1, 0);
maxCount--;
if (maxCount < 0) {
return false;
}
} else {
minCount = Math.max(minCount - 1, 0);
maxCount++;
}
}
return minCount == 0;
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是字符串 s 的长度。需要遍历字符串一次。
- 空间复杂度:\(O(1)\)。
1249. 移除无效的括号
给你一个由 '('、')' 和小写字母组成的字符串 s。
你需要从字符串中删除最少数目的 '(' 或者 ')' (可以删除任意位置的括号),使得剩下的「括号字符串」有效。
请返回任意一个合法字符串。
有效「括号字符串」应当符合以下 任意一条 要求:
空字符串或只包含小写字母的字符串
可以被写作 AB(A 连接 B)的字符串,其中 A 和 B 都是有效「括号字符串」
可以被写作 (A) 的字符串,其中 A 是一个有效的「括号字符串」
示例 1:
输入:s = "lee(t(c)o)de)"
输出:"lee(t(c)o)de"
解释:"lee(t(co)de)" , "lee(t(c)ode)" 也是一个可行答案。
示例 2:
输入:s = "a)b(c)d"
输出:"ab(c)d"
示例 3:
输入:s = "))(("
输出:""
解释:空字符串也是有效的
答案
用操作栈去记录所有待操作的左括号,遇到右括号就出栈。操作栈记录左括号的下标,方便删除。
- 多余的右括号置为0
- 遍历完剩下的多余的左括号也置为0
class Solution {
public String minRemoveToMakeValid(String s) {
Stack<Integer> leftStack = new Stack<>();
StringBuilder sb = new StringBuilder();
char[] chars = s.toCharArray();
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '(') {
leftStack.push(i);
} else if (chars[i] == ')') {
// 多出来的右括号需要全部去掉
if (leftStack.isEmpty()) {
chars[i] = 0;
} else {
leftStack.pop();
}
}
}
// 多出来的左括号需要全部去掉
while (!leftStack.isEmpty()) {
chars[leftStack.pop()] = 0;
}
for (char c : chars) {
if (c != 0) {
sb.append(c);
}
}
return sb.toString();
}
}
921. 使括号有效的最少添加
只有满足下面几点之一,括号字符串才是有效的:
它是一个空字符串,或者
它可以被写成 AB (A 与 B 连接), 其中 A 和 B 都是有效字符串,或者
它可以被写作 (A),其中 A 是有效字符串。
给定一个括号字符串 s ,移动N次,你就可以在字符串的任何位置插入一个括号。
例如,如果 s = "()))" ,你可以插入一个开始括号为 "(()))" 或结束括号为 "())))" 。
返回 为使结果字符串 s 有效而必须添加的最少括号数。
示例 1:
输入:s = "())"
输出:1
示例 2:
输入:s = "((("
输出:3
我的
class Solution {
public int minAddToMakeValid(String s) {
char[] chars = s.toCharArray();
int res = 0;
Stack<Character> stack = new Stack<>();
for (char c : chars) {
if (c == '(') {
stack.push(c);
} else {
if (!stack.isEmpty()) {
stack.pop();
} else {
// 多余的右括号
res++;
}
}
}
// 多余的右括号 + 多余的左括号
return res + stack.size();
}
}
2116. 判断一个括号字符串是否有效
一个括号字符串是只由 '(' 和 ')' 组成的 非空 字符串。如果一个字符串满足下面 任意 一个条件,那么它就是有效的:
- 字符串为 ().
- 它可以表示为 AB(A 与 B 连接),其中A 和 B 都是有效括号字符串。
- 它可以表示为 (A) ,其中 A 是一个有效括号字符串。
给你一个括号字符串 s 和一个字符串 locked ,两者长度都为 n 。locked 是一个二进制字符串,只包含 '0' 和 '1' 。对于 locked 中 每一个 下标 i :
- 如果 locked[i] 是 '1' ,你 不能 改变 s[i] 。
- 如果 locked[i] 是 '0' ,你 可以 将 s[i] 变为 '(' 或者 ')' 。
- 如果你可以将 s 变为有效括号字符串,请你返回 true ,否则返回 false 。
示例 1:
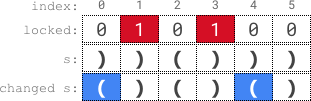
输入:s = "))()))", locked = "010100"
输出:true
解释:locked[1] == '1' 和 locked[3] == '1' ,所以我们无法改变 s[1] 或者 s[3] 。
我们可以将 s[0] 和 s[4] 变为 '(' ,不改变 s[2] 和 s[5] ,使 s 变为有效字符串。
示例 2:
输入:s = "()()", locked = "0000"
输出:true
解释:我们不需要做任何改变,因为 s 已经是有效字符串了。
示例 3:
输入:s = ")", locked = "0"
输出:false
解释:locked 允许改变 s[0] 。
但无论将 s[0] 变为 '(' 或者 ')' 都无法使 s 变为有效字符串。
错误
下面的这种做法是错误的,忽略了左括号的可变性!
class Solution {
public boolean canBeValid(String s, String locked) {
Stack<Integer> stack = new Stack<>();
char[] sChar = s.toCharArray();
char[] lockedChar = locked.toCharArray();
for (int i = 0; i < sChar.length; i++) {
if (sChar[i] == '(') {
stack.push(i);
} else {
if (stack.isEmpty()) {
if (lockedChar[i] == '0') {
stack.push(i);
} else {
return false;
}
} else {
stack.pop();
}
}
}
while (stack.size() % 2 == 0 && !stack.isEmpty()) {
if (lockedChar[stack.pop()] == '0') {
stack.pop();
} else {
return false;
}
}
return stack.isEmpty();
}
}
答案
首先我们需要明确的是,这种题,不可变的左括号和右括号,才是决定结果、需要主要讨论的对象。
贪心算法:
- 有效括号:****所有左括号的右边都有与之相匹配的右括号,并且 所有右括号的左边也都有与之相匹配的左括号。
- 顺序遍历:证明所有不可变右括号的左边都有与之相对应的左括号或可变括号相匹配;
- 逆序遍历:证明所有不可变左括号的右边都有与之相对应的右括号或可变括号相匹配。
首先 s 长度不能为奇数,此时应直接返回 \(\texttt{false}\)。
然后就是用括号问题的经典技巧了:判断 s 是否为有效括号字符串,可以正序遍历 s,用一个变量 x 记录括号的平衡度,遇到左括号就加一,右括号就减一。要求 x 在任意时刻不能是负数,且遍历结束时 \(x=0\)。
本题可以将部分括号变成左括号或者右括号(下文称作可变括号),我们可以将这些可变括号的个数暂存下来(不改变 x 的值),如果后面遇到 x 要变为负数的情况,则将前面的一个可变括号变为左括号,若此时没有剩余的可变括号,则说明我们无法将 s 变为有效括号字符串。
如果遍历结束后还剩下可变括号,可以将其与其他可变括号配对,或者与剩下的左括号配对。这种配对方式可以让最终的 \(x=0\)。但是这种做法会漏掉左括号比右括号多的情况,这种情况下我们是无法区分 \(\texttt{*(}\) 和 \(\texttt{(*}\) 的,这里 \(\texttt{*}\) 表示可变括号,所以我们还需要反着再遍历一次,从而涵盖所有情况。
class Solution {
// 思想:从左向右扫描处理固定不可变的右括号,从右向左扫描处理固定不可变的左括号
// 若固定的括号都可以匹配,则匹配成功
public boolean canBeValid(String s, String locked) {
int sLength = s.length();
if (sLength % 2 == 1) {
return false;
}
// 注:由于这里 len(s) 是偶数,所以循环结束后 x 也是偶数(这意味着可以通过配对来让括号平衡度为 0),无需判断 x 是否为奇数
// x 是偶数是因为每遍历一个字符必然会改变 x 的奇偶性,而 x 的奇偶性在发生偶数次变化后的结果是 x 的奇偶性不变
int x = 0; // 充当栈使用
// 观察不可变右括号是否有括号与之匹配
// 可变符号充当左括号
for (int i = 0; i < sLength; i++) {
if (s.charAt(i) == '(' || locked.charAt(i) == '0') {
x++; // 可变符号均作为左括号
} else { // 不可变的右括号
if (x > 0) {
x--;
} else {
return false;
}
}
}
x = 0;
// 观察不可变左括号是否有括号可以与之匹配
// 可变符号充当右括号
for (int i = sLength - 1; i >= 0; i--) {
if (s.charAt(i) == ')' || locked.charAt(i) == '0') {
x++; // 可变符号均作为右括号
} else {
if (x > 0) {
x--;
} else {
return false;
}
}
}
return true;
}
}
我的
题目中总共有三种类型的元素:
- 不可变左括号
- 不可变右括号
- 可变符号
我们需要使用两个栈来分别存放不可变左括号和可变符号,分开讨论
class Solution {
public boolean canBeValid(String s, String locked) {
int length = s.length();
if (length % 2 == 1) {
return false;
}
// 存放左括号
Stack<Integer> leftStack = new Stack<>();
// 存放可变符号
Stack<Integer> starStack = new Stack<>();
// 可变符号充当左括号
for (int i = 0; i < length; i++) {
char c = s.charAt(i);
char isLocked = locked.charAt(i);
if (c == '(' && isLocked == '1') {
leftStack.push(i);
} else if (c == ')' && isLocked == '1') {
if (!leftStack.isEmpty()) {
leftStack.pop();
} else if (!starStack.isEmpty()) {
starStack.pop();
} else {
return false;
}
} else {
starStack.push(i);
}
}
// 可变符号充当右括号
while (!leftStack.isEmpty() && !starStack.isEmpty()) {
int leftIndex = leftStack.pop();
int starIndex = starStack.pop();
if (leftIndex > starIndex) {
return false;
}
}
return leftStack.isEmpty();
}
}
32. 最长有效括号
给你一个只包含 '(' 和 ')' 的字符串,找出最长有效(格式正确且连续)括号子串的长度。
示例 1:
输入:s = "(()"
输出:2
解释:最长有效括号子串是 "()"
示例 2:
输入:s = ")()())"
输出:4
解释:最长有效括号子串是 "()()"
示例 3:
输入:s = ""
输出:0
方法一:动态规划
思路和算法
我们定义 \(\textit{dp}[i]\) 表示以下标 i 字符结尾的最长有效括号的长度。我们将 \(\textit{dp}\) 数组全部初始化为 0 。显然有效的子串一定以 \(\text{‘)’}\) 结尾,因此我们可以知道以 \(\text{‘(’}\) 结尾的子串对应的 \(\textit{dp}\) 值必定为 0 ,我们只需要求解 \(\text{‘)’}\) 在 \(\textit{dp}\) 数组中对应位置的值。
我们从前往后遍历字符串求解 \(\textit{dp}\) 值,我们每两个字符检查一次:
1.\(s[i] = \text{‘)’}\) 且 \(s[i - 1] = \text{‘(’}\),也就是字符串形如 \(“……()”\),我们可以推出:
我们可以进行这样的转移,是因为结束部分的 "()" 是一个有效子字符串,并且将之前有效子字符串的长度增加了 2 。
2.\(s[i] = \text{‘)’}\) 且 \(s[i - 1] = \text{‘)’}\),也就是字符串形如 \(“……))”\),我们可以推出:
如果 \(s[i - \textit{dp}[i - 1] - 1] = \text{‘(’}\),那么
我们考虑如果倒数第二个 \(\text{‘)’}\) 是一个有效子字符串的一部分(记作 \(sub_s\)),对于最后一个 \(\text{‘)’}\) ,如果它是一个更长子字符串的一部分,那么它一定有一个对应的 \(\text{‘(’}\) ,且它的位置在倒数第二个 \(\text{‘)’}\) 所在的有效子字符串的前面(也就是 \(sub_s\) 的前面)。因此,如果子字符串 \(sub_s\) 的前面恰好是 \(\text{‘(’}\) ,那么我们就用 2 加上 \(sub_s\) 的长度(\(\textit{dp}[i-1]\))去更新 \(\textit{dp}[i]\)。同时,我们也会把有效子串 \(“(sub_s)”\))” 之前的有效子串的长度也加上,也就是再加上 \(\textit{dp}[i-\textit{dp}[i-1]-2]\)。
最后的答案即为 \(\textit{dp}\) 数组中的最大值。
class Solution {
public int longestValidParentheses(String s) {
int maxans = 0;
int[] dp = new int[s.length()];
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]);
}
}
return maxans;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 为字符串的长度。我们只需遍历整个字符串一次,即可将 \(\textit{dp}\) 数组求出来。
-
空间复杂度:\(O(n)\)。我们需要一个大小为 n 的 \(\textit{dp}\) 数组。
方法二:栈
思路和算法
撇开方法一提及的动态规划方法,相信大多数人对于这题的第一直觉是找到每个可能的子串后判断它的有效性,但这样的时间复杂度会达到 \(O(n^3)\)),无法通过所有测试用例。但是通过栈,我们可以在遍历给定字符串的过程中去判断到目前为止扫描的子串的有效性,同时能得到最长有效括号的长度。
具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」,这样的做法主要是考虑了边界条件的处理,栈里其他元素维护左括号的下标:
- 对于遇到的每个 \(\text{‘(’}\),我们将它的下标放入栈中
- 对于遇到的每个 \(\text{‘)’}\),我们先弹出栈顶元素表示匹配了当前右括号:
- 如果栈为空,说明当前的右括号为没有被匹配的右括号,我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
- 如果栈不为空,当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
我们从前往后遍历字符串并更新答案即可。
需要注意的是,如果一开始栈为空,第一个字符为左括号的时候我们会将其放入栈中,这样就不满足提及的「最后一个没有被匹配的右括号的下标」,为了保持统一,我们在一开始的时候往栈中放入一个值为 -1 的元素。
class Solution {
public int longestValidParentheses(String s) {
char[] chars = s.toCharArray();
int max = 0;
Stack<Integer> stack = new Stack<>();
stack.push(-1); // 初始边界
// (() 和 )() 有效长度都是2,需要记录最后一个无法配对的括号的下标?
// 可是左括号无法知道他当前是否无法配对呀,但是按照左括号入栈,可以在出栈后,当前元素-栈顶元素,得到有效长度!问题是右括号入不了栈
// 那就让出栈后,栈为空时,当前右括号下标可以入栈,作为栈底,充当计算长度的边界
for (int i = 0; i < chars.length; i++) {
if (chars[i] == '(') {
stack.push(i);
} else {
// 抵消左括号
stack.pop();
if (!stack.isEmpty()) {
max = Math.max(max, i - stack.peek());
} else {
// 将不匹配的右括号压入栈底充当边界
stack.push(i);
}
}
}
return max;
}
}
复杂度分析
- 时间复杂度:\(O(n)\),n 是给定字符串的长度。我们只需要遍历字符串一次即可。
- 空间复杂度:\(O(n)\)。栈的大小在最坏情况下会达到 n,因此空间复杂度为 \(O(n)\)。
方法三:不需要额外的空间
思路和算法
在此方法中,我们利用两个计数器 \(\textit{left}\) 和 \(\textit{right}\) 。首先,我们从左到右遍历字符串,对于遇到的每个 \(\text{‘(’}\),我们增加 \(\textit{left}\) 计数器,对于遇到的每个 \(\text{‘)’}\) ,我们增加 \(\textit{right}\) 计数器。每当 \(\textit{left}\) 计数器与 \(\textit{right}\) 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串。当 \(\textit{right}\) 计数器比 \(\textit{left}\) 计数器大时,我们将 \(\textit{left}\) 和 \(\textit{right}\) 计数器同时变回 0。
这样的做法贪心地考虑了以当前字符下标结尾的有效括号长度,每次当右括号数量多于左括号数量的时候之前的字符我们都扔掉不再考虑,重新从下一个字符开始计算,但这样会漏掉一种情况,就是遍历的时候左括号的数量始终大于右括号的数量,即 (() ,这种时候最长有效括号是求不出来的。
解决的方法也很简单,我们只需要从右往左遍历用类似的方法计算即可,只是这个时候判断条件反了过来:
- 当 \(\textit{left}\) 计数器比 \(\textit{right}\) 计数器大时,我们将 \(\textit{left}\) 和 \(\textit{right}\) 计数器同时变回 0
- 当 \(\textit{left}\) 计数器与 \(\textit{right}\) 计数器相等时,我们计算当前有效字符串的长度,并且记录目前为止找到的最长子字符串
这样我们就能涵盖所有情况从而求解出答案。
class Solution {
public int longestValidParentheses(String s) {
int left = 0, right = 0, maxlength = 0;
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * right);
} else if (right > left) {
left = right = 0;
}
}
left = right = 0;
for (int i = s.length() - 1; i >= 0; i--) {
if (s.charAt(i) == '(') {
left++;
} else {
right++;
}
if (left == right) {
maxlength = Math.max(maxlength, 2 * left);
} else if (left > right) {
left = right = 0;
}
}
return maxlength;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 为字符串长度。我们只要正反遍历两边字符串即可。
-
空间复杂度:\(O(1)\)。我们只需要常数空间存放若干变量。
中缀表达式转换为后缀表达式
中缀表达式转换为前缀或后缀表达式:(手工做法)
- 按照运算符的优先级对所有的运算单位加括号。
- 转换为前缀或后缀表达式
- 前缀:把运算符号移动到对应的括号前面
- 后缀:把运算符号移动到对应的括号后面
在中缀表达式转化为相应的后缀表达式,需要根据操作符<op>的优先级来进行栈的变化:
栈外优先级icp(in coming priority, icp):表示当前扫描到的运算符ch的优先级;
栈内优先级isp(in stack priority, isp):为该运算符进栈后的优先级。
这个优先级其实也很简单,就是一般的运算优先级,有括号先算括号、先乘除后加减、同级运算从左往右依次运算。
| 操作符 | # | ( | *,/ | +,- | ) |
|---|---|---|---|---|---|
| 栈外优先级icp | 0 | 6 | 4 | 2 | 1 |
| 栈内优先级isp | 0 | 1 | 5 | 3 | 6 |
- icp>isp:进栈,读下一个字符
icp=isp:pop,不输出(#,(,))
icp<isp:出栈并输出
如a+b-a*((c+d)/e-f)+g转换为ab+acd+e/f-*-g
+-*((+(按优先级进入的)
+号遇到-号之后运算了,后面的不能算得看下一个,遇到)能算了。所以栈中存的暂时还不能确定运算次序的操作符最多则5个。
中缀表达式转换为后缀表达式:(程序做法)
- 从左向右开始扫描中缀表达式
- 遇到数字时,加入后缀表达式
- 遇到运算符时:按照运算符的优先级进行操作
- 若当前扫描元素优先级>栈顶元素,那么当前扫描元素就入栈,先处理当前扫描元素,再处理栈顶元素
- 若当前扫描元素优先级<栈顶元素,那么栈顶元素就出栈,先处理栈顶元素,再处理当前扫描元素
- 若当前扫描元素优先级=栈顶元素,那么pop,不输出
- 若为'(',入栈
- 若为')',则依次把栈中的运算符出栈,并加入后缀表达式,直到出现'(',从栈中删除'(';
- 若为除括号外的其他运算符,当其优先级高于除'('以外的栈顶运算符时,直接入栈;
否则从栈顶开始,依次弹出比当前处理的运算符优先级高和优先级相等的运算符,直到一个比它优先级低的或遇到了一个左括号为止。
- 当扫描的中缀表达式结束时,栈中的所有运算符依次出栈加入后缀表达式。
| 待处理序列 | 当前扫描元素 | 后缀表达式 | 栈 | 动作 |
|---|
依次扫描,扫描元素优先级高的入栈;扫描元素优先级低,先让优先级较高的栈顶元素处理
理解:优先级的单调栈
剑指 Offer II 036. 后缀表达式
根据 逆波兰表示法,求该后缀表达式的计算结果。
有效的算符包括 +、-、*、/ 。每个运算对象可以是整数,也可以是另一个逆波兰表达式。
说明:
整数除法只保留整数部分。
给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:tokens = ["2","1","+","3","*"]
输出:9
解释:该算式转化为常见的中缀算术表达式为:((2 + 1) * 3) = 9
示例 2:
输入:tokens = ["4","13","5","/","+"]
输出:6
解释:该算式转化为常见的中缀算术表达式为:(4 + (13 / 5)) = 6
示例 3:
输入:tokens = ["10","6","9","3","+","-11","*","/","*","17","+","5","+"]
输出:22
解释:
该算式转化为常见的中缀算术表达式为:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
方法一:栈
后缀表达式由波兰的逻辑学家卢卡西维兹提出,也称逆波兰表达式。后缀表达式的特点是:没有括号,运算符总是放在和它相关的操作数之后。
后缀表达式严格遵循「从左到右」的运算。计算后缀表达式的值时,使用一个栈存储操作数,从左到右遍历后缀表达式,进行如下操作:
如果遇到操作数,则将操作数入栈;
如果遇到运算符,则将两个操作数出栈,其中先出栈的是右操作数,后出栈的是左操作数,使用运算符对两个操作数进行运算,将运算得到的新操作数入栈。
整个后缀表达式遍历完毕之后,栈内只有一个元素,该元素即为后缀表达式的值。
class Solution {
public int evalRPN(String[] tokens) {
Stack<Integer> stack = new Stack<Integer>();
int n = tokens.length;
for (int i = 0; i < n; i++) {
String token = tokens[i];
if (isNumber(token)) {
stack.push(Integer.valueOf(token));
} else {
int num2 = stack.pop();
int num1 = stack.pop();
switch (token) {
case "+":
stack.push(num1 + num2);
break;
case "-":
stack.push(num1 - num2);
break;
case "*":
stack.push(num1 * num2);
break;
case "/":
stack.push(num1 / num2);
break;
default:
}
}
}
return stack.pop();
}
public boolean isNumber(String token) {
return !("+".equals(token) || "-".equals(token) || "*".equals(token) || "/".equals(token));
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{tokens}\) 的长度。需要遍历数组 \(\textit{tokens}\) 一次,计算后缀表达式的值。
- 空间复杂度:\(O(n)\),其中 n 是数组 \(\textit{tokens}\) 的长度。使用栈存储计算过程中的数,栈内元素个数不会超过后缀表达式的长度。
方法二:数组模拟栈
方法一使用栈存储操作数。也可以使用一个数组模拟栈操作。
如果使用数组代替栈,则需要预先定义数组的长度。对于长度为 n 的后缀表达式,显然栈内元素个数不会超过 n,但是将数组的长度定义为 n 仍然超过了栈内元素个数的上界。那么,栈内元素最多可能有多少个?
对于一个有效的后缀表达式,其长度 n 一定是奇数,且操作数的个数一定比运算符的个数多 1 个,即包含 \(\frac{n+1}{2}\) 个操作数和 \(\frac{n-1}{2}\) 个运算符。考虑遇到操作数和运算符时,栈内元素个数分别会如何变化:
- 如果遇到操作数,则将操作数入栈,因此栈内元素增加 1 个;
- 如果遇到运算符,则将两个操作数出栈,然后将一个新操作数入栈,因此栈内元素先减少 2 个再增加 1 个,结果是栈内元素减少 1 个。
由此可以得到操作数和运算符与栈内元素个数变化的关系:遇到操作数时,栈内元素增加 1 个;遇到运算符时,栈内元素减少 1 个。
最坏情况下,\(\frac{n+1}{2}\) 个操作数都在表达式的前面,\(\frac{n-1}{2}\) 个运算符都在表达式的后面,此时栈内元素最多为 \(\frac{n+1}{2}\) 个。在其余情况下,栈内元素总是少于 \(\frac{n+1}{2}\) 个。因此,在任何情况下,栈内元素最多可能有 \(\frac{n+1}{2}\) 个,将数组的长度定义为 \(\frac{n+1}{2}\) 即可。
具体实现方面,创建数组 \(\textit{stack}\) 模拟栈,数组下标 0 的位置对应栈底,定义 \(\textit{index}\) 表示栈顶元素的下标位置,初始时栈为空,\(\textit{index}=-1\)。当遇到操作数和运算符时,进行如下操作:
如果遇到操作数,则将 \(\textit{index}\) 的值加 1,然后将操作数赋给 \(\textit{stack}[\textit{index}]\);
如果遇到运算符,则将 \(\textit{index}\) 的值减 1,此时 \(\textit{stack}[\textit{index}]\) 和 \(\textit{stack}[\textit{index}+1]\) 的元素分别是左操作数和右操作数,使用运算符对两个操作数进行运算,将运算得到的新操作数赋给 \(\textit{stack}[\textit{index}]\)。
整个后缀表达式遍历完毕之后,栈内只有一个元素,因此 \(\textit{index}=0\),此时 \(\textit{stack}[\textit{index}]\) 即为后缀表达式的值。
class Solution {
public int evalRPN(String[] tokens) {
int n = tokens.length;
int[] stack = new int[(n + 1) / 2];
int index = -1;
for (int i = 0; i < n; i++) {
String token = tokens[i];
switch (token) {
case "+":
index--;
stack[index] += stack[index + 1];
break;
case "-":
index--;
stack[index] -= stack[index + 1];
break;
case "*":
index--;
stack[index] *= stack[index + 1];
break;
case "/":
index--;
stack[index] /= stack[index + 1];
break;
default:
index++;
stack[index] = Integer.parseInt(token);
}
}
return stack[index];
}
}
复杂度分析
- 时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{tokens}\) 的长度。需要遍历数组 \(\textit{tokens}\) 一次,计算后缀表达式的值。
- 空间复杂度:\(O(n)\),其中 n 是数组 \(\textit{tokens}\) 的长度。需要创建长度为 \(\frac{n+1}{2}\) 的数组模拟栈操作。
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为: k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例 1:
输入:s = "3[a]2[bc]"
输出:"aaabcbc"
示例 2:
输入:s = "3[a2[c]]"
输出:"accaccacc"
示例 3:
输入:s = "2[abc]3[cd]ef"
输出:"abcabccdcdcdef"
示例 4:
输入:s = "abc3[cd]xyz"
输出:"abccdcdcdxyz"
答案
本题中可能出现括号嵌套的情况,比如 2[a2[bc]],这种情况下我们可以先转化成 2[abcbc],在转化成 abcbcabcbc。我们可以把字母、数字和括号看成是独立的 TOKEN,并用栈来维护这些 TOKEN。具体的做法是,遍历这个栈:
- 如果当前的字符为数位,解析出一个数字(连续的多个数位)并进栈
- 如果当前的字符为字母或者左括号,直接进栈
- 如果当前的字符为右括号,开始出栈,一直到左括号出栈,出栈序列反转后拼接成一个字符串,此时取出栈顶的数字(此时栈顶一定是数字,想想为什么?),就是这个字符串应该出现的次数,我们根据这个次数和字符串构造出新的字符串并进栈
重复如上操作,最终将栈中的元素按照从栈底到栈顶的顺序拼接起来,就得到了答案。注意:这里可以用不定长数组来模拟栈操作,方便从栈底向栈顶遍历。
class Solution {
int ptr;
public String decodeString(String s) {
LinkedList<String> stk = new LinkedList<String>();
ptr = 0;
while (ptr < s.length()) {
char cur = s.charAt(ptr);
if (Character.isDigit(cur)) {
// 获取一个数字并进栈
String digits = getDigits(s);
stk.addLast(digits);
} else if (Character.isLetter(cur) || cur == '[') {
// 获取一个字母并进栈
stk.addLast(String.valueOf(s.charAt(ptr++)));
} else {
++ptr;
LinkedList<String> sub = new LinkedList<String>();
while (!"[".equals(stk.peekLast())) {
sub.addLast(stk.removeLast());
}
Collections.reverse(sub);
// 左括号出栈
stk.removeLast();
// 此时栈顶为当前 sub 对应的字符串应该出现的次数
int repTime = Integer.parseInt(stk.removeLast());
StringBuffer t = new StringBuffer();
String o = getString(sub);
// 构造字符串
while (repTime-- > 0) {
t.append(o);
}
// 将构造好的字符串入栈
stk.addLast(t.toString());
}
}
return getString(stk);
}
public String getDigits(String s) {
StringBuffer ret = new StringBuffer();
while (Character.isDigit(s.charAt(ptr))) {
ret.append(s.charAt(ptr++));
}
return ret.toString();
}
public String getString(LinkedList<String> v) {
StringBuffer ret = new StringBuffer();
for (String s : v) {
ret.append(s);
}
return ret.toString();
}
}
复杂度分析
- 时间复杂度:记解码后得出的字符串长度为 S,除了遍历一次原字符串 s,我们还需要将解码后的字符串中的每个字符都入栈,并最终拼接进答案中,故渐进时间复杂度为 \(O(S+|s|)\),即 \(O(S)\)。
- 空间复杂度:记解码后得出的字符串长度为 S,这里用栈维护 TOKEN,栈的总大小最终与 S 相同,故渐进空间复杂度为 \(O(S)\)。
我的
个人觉得我的方法更好一点,将 数字栈 和 字符串栈 分开存放,各存各的,然后再进行合并。
操作栈:
- 操作数栈:存放括号和字母,如
[abc] - 操作符栈:存放数字,代表操作重复次数。
遍历字符
- 将数字进行组合,碰到
[后,存放在数字栈中 - 将字符放在字符串栈中,碰到
]后,取出来组合,再存放在字符串栈中
class Solution {
public String decodeString(String s) {
Stack<Integer> numStack = new Stack<>();
Stack<String> strStack = new Stack<>();
char[] chars = s.toCharArray();
int num = 0;
for (int i = 0; i < chars.length; i++) {
if (chars[i] >= '0' && chars[i] <= '9') {
// 这里需要特别注意不能使用Integer.valueOf(chars[i])
// 因为char类型本就是数字,这样解出来的会是char的ASCII码
num = num * 10 + chars[i] - '0';
} else if (chars[i] == '[') {
numStack.push(num);
num = 0;
strStack.push("[");
} else if (chars[i] == ']') {
StringBuilder sb = new StringBuilder();
while (strStack.peek() != "[") {
sb.insert(0, strStack.pop());
}
strStack.pop();
String str = sb.toString();
int count = numStack.pop();
for (int j = 1; j < count; j++) {
sb.append(str);
}
strStack.push(sb.toString());
} else { // 字母
strStack.push(String.valueOf(chars[i]));
}
}
StringBuilder sb = new StringBuilder();
while (!strStack.isEmpty()) {
sb.insert(0, strStack.pop());
}
return sb.toString();
}
}
1190. 反转每对括号间的子串
给出一个字符串 s(仅含有小写英文字母和括号)。
请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。
注意,您的结果中 不应 包含任何括号。
示例 1:
输入:s = "(abcd)"
输出:"dcba"
示例 2:
输入:s = "(u(love)i)"
输出:"iloveu"
解释:先反转子字符串 "love" ,然后反转整个字符串。
示例 3:
输入:s = "(ed(et(oc))el)"
输出:"leetcode"
解释:先反转子字符串 "oc" ,接着反转 "etco" ,然后反转整个字符串。
示例 4:
输入:s = "a(bcdefghijkl(mno)p)q"
输出:"apmnolkjihgfedcbq"
我的双端队列
class Solution {
public String reverseParentheses(String s) {
Deque<String> stack = new LinkedList<>();
StringBuilder sb = null;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(') {
stack.offerLast("(");
} else if (c == ')') {
sb = new StringBuilder();
while (!stack.isEmpty() && !stack.peekLast().equals("(")) {
StringBuilder temp = new StringBuilder(stack.pollLast());
sb.append(temp.reverse().toString());
}
if (stack.peekLast().equals("(")) {
stack.pollLast();
stack.offerLast(sb.toString());
}
} else {
stack.offerLast(String.valueOf(c));
}
}
// 顺序出队
sb = new StringBuilder();
while (!stack.isEmpty()) {
sb.append(stack.pollFirst());
}
return sb.toString();
}
}
答案
思路及算法
本题要求按照从括号内到外的顺序进行处理。如字符串 (u(love)i),首先处理内层括号,变为 (uevoli),然后处理外层括号,变为 iloveu。
对于括号序列相关的题目,通用的解法是使用递归或栈。本题中我们将使用栈解决。
我们从左到右遍历该字符串,使用字符串 str 记录当前层所遍历到的小写英文字母。对于当前遍历的字符:
-
如果是左括号,将 str 插入到栈中,并将 str 置为空,进入下一层;
-
如果是右括号,则说明遍历完了当前层,需要将 str 反转,返回给上一层。具体地,将栈顶字符串弹出,然后将反转后的 str 拼接到栈顶字符串末尾,将结果赋值给 str。
-
如果是小写英文字母,将其加到 str 末尾。
注意到我们仅在遇到右括号时才进行字符串处理,这样可以保证我们是按照从括号内到外的顺序处理字符串。
class Solution {
public String reverseParentheses(String s) {
Deque<String> stack = new LinkedList<String>();
StringBuffer sb = new StringBuffer();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (ch == '(') { // 如果遇到新的一个左括号,那就先将sb中的字符串放入栈中暂存起来,先处理新的括号
stack.push(sb.toString());
sb.setLength(0);
} else if (ch == ')') { // 如果遇到右括号,那就将字符串反转,并且头插之前栈中的字符串
sb.reverse();
sb.insert(0, stack.pop());
} else { // 遇到字母就加入sb中
sb.append(ch);
}
}
return sb.toString();
}
}
735. 行星碰撞
给定一个整数数组 asteroids,表示在同一行的行星。
对于数组中的每一个元素,其绝对值表示行星的大小,正负表示行星的移动方向(正表示向右移动,负表示向左移动)。每一颗行星以相同的速度移动。
找出碰撞后剩下的所有行星。碰撞规则:两个行星相互碰撞,较小的行星会爆炸。如果两颗行星大小相同,则两颗行星都会爆炸。两颗移动方向相同的行星,永远不会发生碰撞。
示例 1:
输入:asteroids = [5,10,-5]
输出:[5,10]
解释:10 和 -5 碰撞后只剩下 10 。 5 和 10 永远不会发生碰撞。
示例 2:
输入:asteroids = [8,-8]
输出:[]
解释:8 和 -8 碰撞后,两者都发生爆炸。
示例 3:
输入:asteroids = [10,2,-5]
输出:[10]
解释:2 和 -5 发生碰撞后剩下 -5 。10 和 -5 发生碰撞后剩下 10 。
我的
class Solution {
public int[] asteroidCollision(int[] asteroids) {
// 栈?
Deque<Integer> stack = new LinkedList<>();
for (int i = 0; i < asteroids.length; i++) {
if (stack.isEmpty() || stack.peek() * asteroids[i] > 0 || asteroids[i] > 0) {
stack.push(asteroids[i]);
} else {
if (stack.peek() < -asteroids[i]) {
stack.pop();
i--;
} else if (stack.peek() == -asteroids[i]) {
stack.pop();
}
}
}
int size = stack.size();
int[] ans = new int[size];
for (int i = size - 1; i >= 0; i--) {
ans[i] = stack.pop();
}
return ans;
}
}
单调栈
一种特殊的栈,在栈的「先进后出」规则基础上,要求「从 栈顶 到 栈底 的元素是 单调递增(或者单调递减) 」。其中,满足从栈顶到栈底的元素是单调递增的栈,叫做「单调递增栈」;满足从栈顶到栈底的元素是单调递减的栈,叫做「单调递减栈」。
技巧:入栈的元素也可以为元素下标,方便我们获取元素位置。
单调栈适用场景
单调栈可以在时间复杂度为\(O(n)\)的情况下,求解出某个元素左边或者右边第一个比它大或者小的元素。
单调栈主要解决下面几种问题
- 比当前元素更大的下一个元素
- 比当前元素更大的前一个元素
- 比当前元素更小的下一个元素
- 比当前元素更小的前一个元素
关键词:下一个大于 xxx、下一个小于 xxx
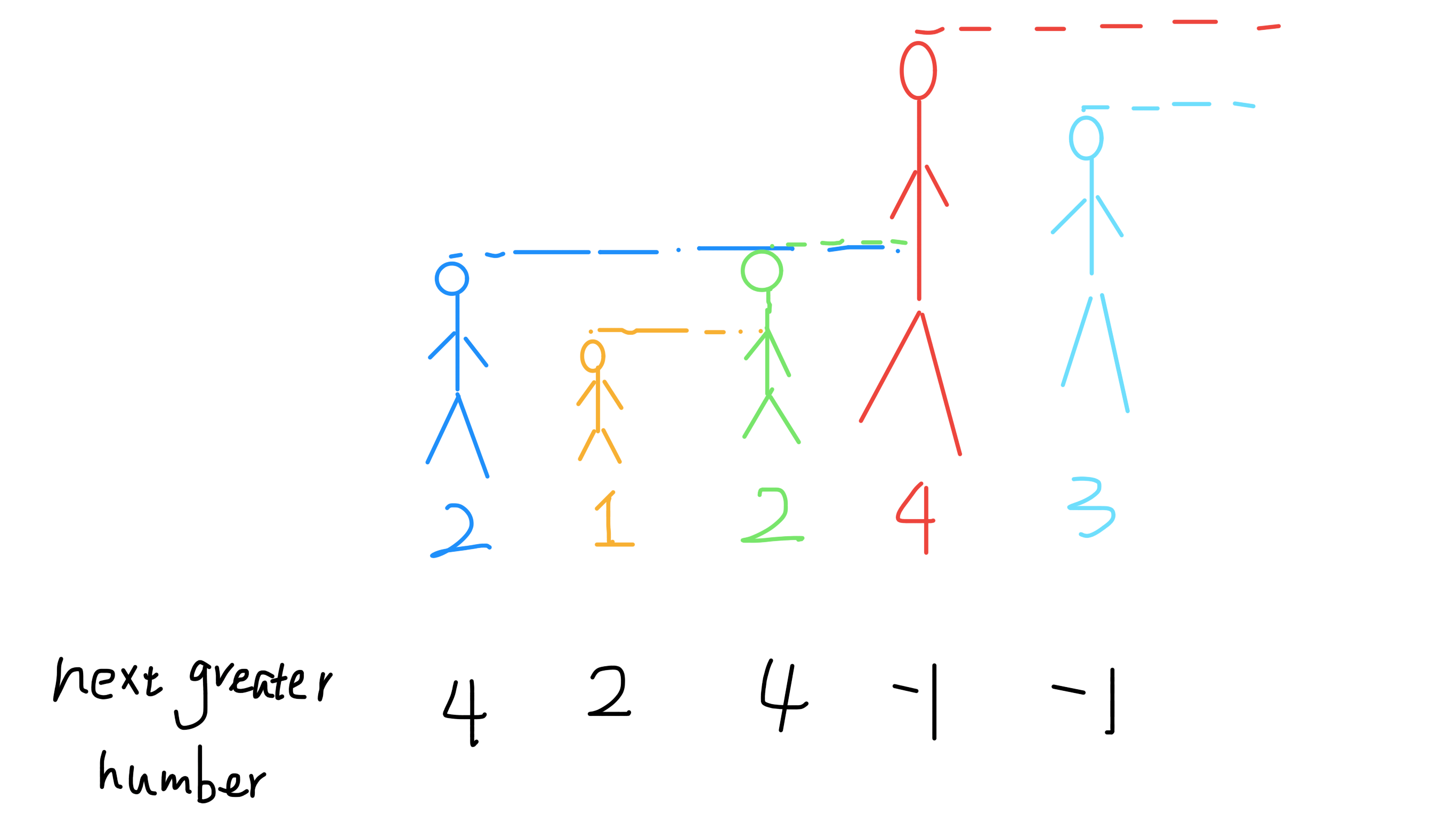
口诀 :
- 查找 「比当前元素大的元素」 就用 单调递减栈,将比当前元素小的元素都暂存入栈中;
- 查找「比当前元素小的元素」就用 单调递增栈,将比当前元素大的元素都暂存入栈中。
- 从 「 左侧 」 查找就看 「 插入栈 」 时的栈顶元素;
- 从 「 右侧 」 查找就看 「 弹出栈 」 时即将插入的元素。
寻找左侧第一个比当前元素大的元素
从左到右遍历元素,构造单调递减栈(从栈底到栈顶递减):一个元素左侧第一个比它大的元素就是将其「插入单调递减栈」时的栈顶元素。如果插入时的栈为空,则说明左侧不存在比当前元素大的元素。
寻找左侧第一个比当前元素小的元素
从左到右遍历元素,构造单调递增栈(从栈底到栈顶递增):一个元素左侧第一个比它小的元素就是将其「插入单调递增栈」时的栈顶元素。如果插入时的栈为空,则说明左侧不存在比当前元素小的元素。
寻找右侧第一个比当前元素大的元素
从左到右遍历元素,构造单调递减栈(从栈底到栈顶递减):一个元素右侧第一个比它大的元素就是将其「弹出单调递减栈」时即将插入的元素。如果该元素没有被弹出栈,则说明右侧不存在比当前元素大的元素。
寻找右侧第一个比当前元素小的元素
从左到右遍历元素,构造单调递增栈(从栈底到栈顶递增):一个元素右侧第一个比它小的元素就是将其「弹出单调递增栈」时即将插入的元素。如果该元素没有被弹出栈,则说明右侧不存在比当前元素小的元素。
单调递增栈(栈底到栈顶单调递增)
单调递增栈 :只有比栈顶元素大的元素才能直接进栈,否则需要先将栈中比当前元素大的元素出栈,再将当前元素入栈。
理解:从栈底到栈顶的元素值是单调递增的。
适用场景:当需要找到当前元素左边第一个和右边第一个比当前元素小的元素时可以使用。(两面包夹芝士)
- 左边第一个小:是栈顶元素的下一层元素(使用前最好先将一个哨兵节点入栈,如 -1,避免对于空栈的额外讨论)
- 右边第一个小:是刚遍历到的、将要入栈的元素
实现思路:
- 首先,每一个元素,无论大小,都需要入栈;
- 然后,每一个元素入栈前,都需要将栈顶不满足条件的元素弹出,再才能入栈。
我的:
public void increasingStack(int[] nums) {
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < nums.length; i++) {
if (stack.isEmpty() || nums[i] >= stack.peek()) { // 当前元素大于栈顶元素就入栈
stack.push(nums[i]);
} else { // 否则,出栈
stack.pop();
i--; // 当前元素继续比较栈顶
}
}
}
Java:循环体内均为单调栈的入栈操作,与上面的方法相比方便拆分入栈与出栈操作
public void increasingStack(int[] nums) {
Stack<Integer> stack = new Stack<>();
for (int num : nums) {
// 循环体内均为单调栈的入栈操作
// 1. 入栈前将当前值小于等于栈顶元素,将栈顶元素弹出
while (!stack.isEmpty() && num <= stack.peek()) {
stack.pop();
}
stack.push(num); // 2. 元素无论大小都是要入栈的
}
}
Python:
def IncreasingStack(nums):
stack = []
for num in nums:
# 当前值小于等于栈顶元素,将栈顶元素弹出
while stack and num <= stack[-1]:
stack.pop()
stack.append(num)
实例:
数组元素:[2, 7, 5, 4, 6, 3, 4, 2],遍历顺序为从左到右。
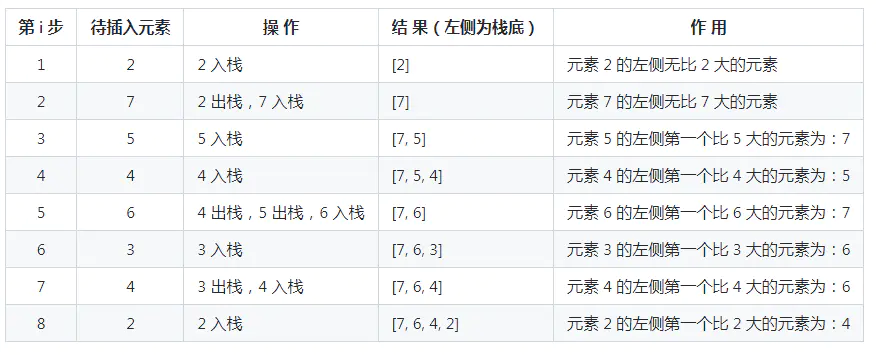
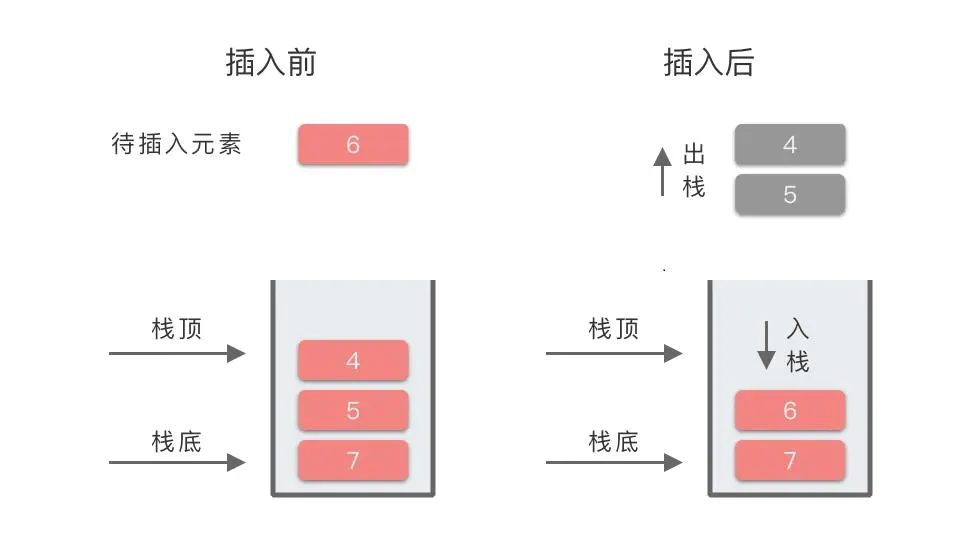
最终栈中元素为 [7, 6, 4, 2]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 2, 4, 6, 7,满足递增关系,所以这是一个单调递增栈。
单调递减栈(栈底到栈顶单调递减)
单调递减栈 :只有比栈顶元素小的元素才能直接进栈,否则需要先将栈中比当前元素小的元素出栈,再将当前元素入栈。
理解:从栈底到栈顶的元素值是单调递减的。
适用场景:当需要找到当前元素左边第一个和右边第一个比当前元素大的元素时可以使用。(两面包夹芝士)
- 左边第一个大:是栈顶元素的下一层元素(使用前最好先将一个哨兵节点入栈,如 -1,避免对于空栈的额外讨论)
- 右边第一个大:是刚遍历到的、将要入栈的元素
我的:
public void decreasingStack(int[] nums) {
Stack<Integer> stack = new Stack<>();
for (int i = 0; i < nums.length; i++) {
if (stack.isEmpty() || nums[i] <= stack.peek()) { // 当前元素小于栈顶元素就入栈
stack.push(nums[i]);
} else { // 否则,出栈
stack.pop();
i--; // 当前元素继续比较栈顶
}
}
}
Java:
public void decreasingStack(int[] nums) {
Stack<Integer> stack = new Stack<>();
for (int num : nums) {
// 循环体内均为单调栈的入栈操作
// 1. 入栈前将当前值大于等于栈顶元素,将栈顶元素弹出
while (!stack.isEmpty() && num >= stack.peek()) {
stack.pop();
}
stack.push(num); // 2. 元素无论大小都是要入栈的
}
}
Python:
def DecreasingStack(nums):
stack = []
for num in nums:
# 当前值大于等于栈顶元素,将栈顶元素弹出
while stack and num >= stack[-1]:
stack.pop()
stack.append(num)
实例:
数组元素:[4, 3, 2, 5, 7, 4, 6, 8],遍历顺序为从左到右。
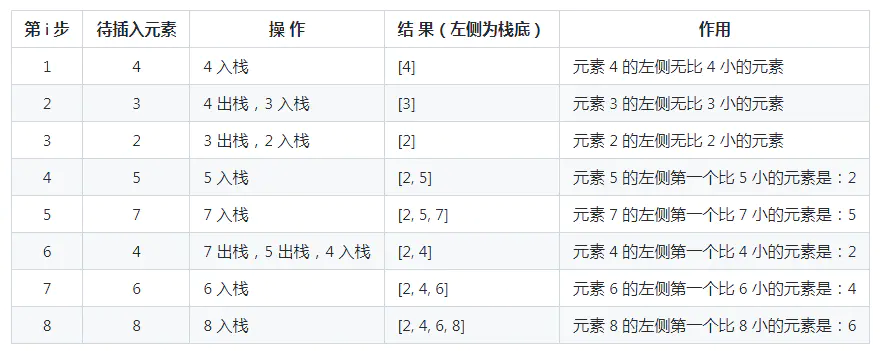
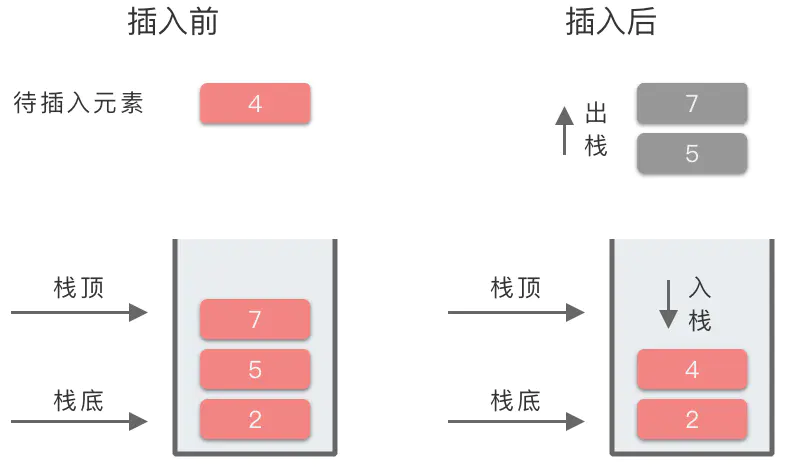
最终栈中元素为 [2, 4, 6, 8]。因为从栈顶(右端)到栈底(左侧)元素的顺序为 8, 6, 4, 2,满足递减关系,所以这是一个单调递减栈。
最大最小值问题:剑指 Offer 30. 最小栈
使用栈或队列可以保存当前状态下的最大最小值,实现最大最小值的O(1)查找。
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.
我的单调栈
适用场景:
- 最大最小值的栈
除了目标栈外,另外建立一个辅助单调栈,来存放目标栈的最大最小值。
以最大值辅助栈为例,我们需要保证栈顶元素为栈内最大值,向下依次递减,非严格降序
- 辅助栈入栈:当目标栈入栈时,对比当前辅助栈栈顶元素,是否比它大,比他大,辅助栈就入栈
- 辅助栈出栈:当目标栈出栈时,对比当前辅助栈栈顶元素,如果相等,那辅助栈就出栈
解题思路:
普通栈的 push() 和 pop() 函数的复杂度为 \(O(1)\) ;而获取栈最小值 min() 函数需要遍历整个栈,复杂度为 O(N)O(N) 。
本题难点: 将 min() 函数复杂度降为 \(O(1)\) ,可通过建立辅助栈实现;
- 数据栈 A : 栈 A 用于存储所有元素,保证入栈 push() 函数、出栈 pop() 函数、获取栈顶 top() 函数的正常逻辑。
- 辅助栈 B : 栈 B 中存储栈 A 中所有 非严格降序 的元素,则栈 A 中的最小元素始终对应栈 B 的栈顶元素,即 min() 函数只需返回栈 B 的栈顶元素即可。
因此,只需设法维护好 栈 B 的元素,使其保持非严格降序,即可实现 min() 函数的 \(O(1)\) 复杂度。
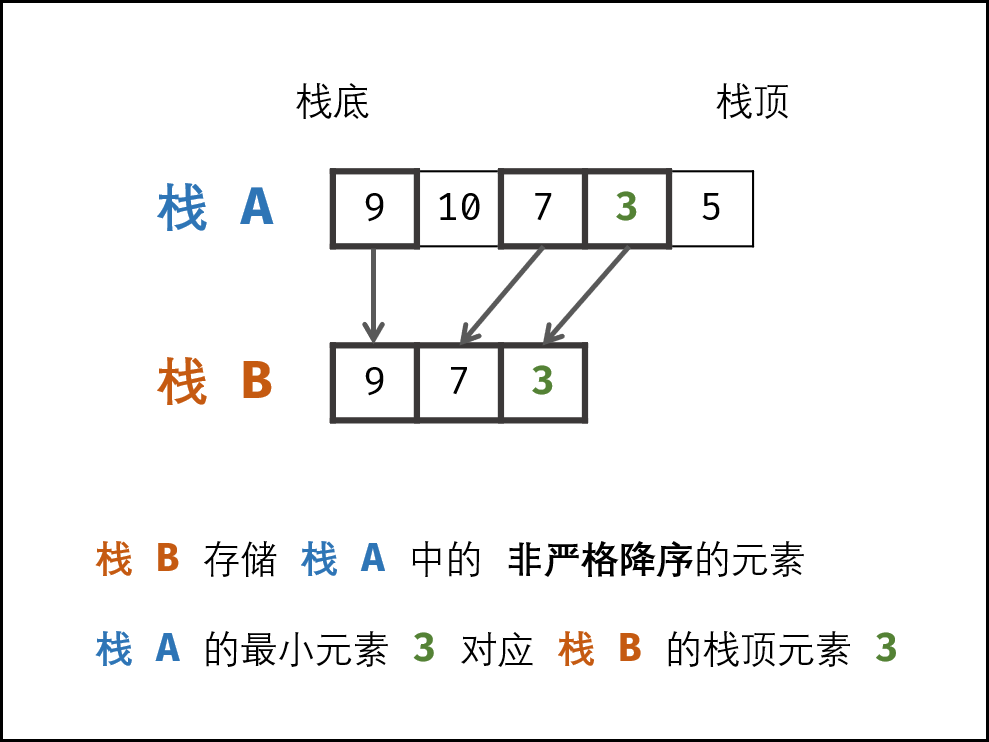
函数设计:
push(x) 函数:重点为保持栈 B 的元素是 非严格降序 的。
- 将 x 压入栈 A (即 A.add(x) );
- 若 ① 栈 B 为空 或 ② x 小于等于 栈 B 的栈顶元素,则将 x 压入栈 B (即 B.add(x) )。
pop() 函数:重点为保持栈 A, B 的 元素一致性 。
- 执行栈 A 出栈(即 A.pop() ),将出栈元素记为 y ;
- 若 y 等于栈 B 的栈顶元素,则执行栈 B 出栈(即 B.pop() )。
top() 函数: 直接返回栈 A 的栈顶元素即可,即返回 A.peek() 。
min() 函数: 直接返回栈 B 的栈顶元素即可,即返回 B.peek() 。
Java 代码中,由于 Stack 中存储的是 int 的包装类 Integer ,因此需要使用 equals() 代替 == 来比较值是否相等。
class MinStack {
Stack<Integer> A, B;
public MinStack() {
A = new Stack<>();
B = new Stack<>(); // 单调栈
}
public void push(int x) {
A.add(x);
// 小于等于单调栈B栈顶元素,那就入栈,保证单调性
if(B.empty() || x <= B.peek())
B.add(x);
}
public void pop() {
// 如果B单调栈中的元素与目标栈A中的元素相等,那就一起出栈
if(A.pop().equals(B.peek()))
B.pop();
}
public int top() {
return A.peek();
}
public int min() {
return B.peek();
}
}
复杂度分析:
- 时间复杂度 \(O(1)\) : push(), pop(), top(), min() 四个函数的时间复杂度均为常数级别。
- 空间复杂度 \(O(N)\) : 当共有 N 个待入栈元素时,辅助栈 B 最差情况下存储 N 个元素,使用 \(O(N)\) 额外空间。
答案
辅助栈
思路
要做出这道题目,首先要理解栈结构先进后出的性质。
对于栈来说,如果一个元素 a 在入栈时,栈里有其它的元素 b, c, d,那么无论这个栈在之后经历了什么操作,只要 a 在栈中,b, c, d 就一定在栈中,因为在 a 被弹出之前,b, c, d 不会被弹出。
因此,在操作过程中的任意一个时刻,只要栈顶的元素是 a,那么我们就可以确定栈里面现在的元素一定是 a, b, c, d。
那么,我们可以在每个元素 a 入栈时把当前栈的最小值 m 存储起来。在这之后无论何时,如果栈顶元素是 a,我们就可以直接返回存储的最小值 m。
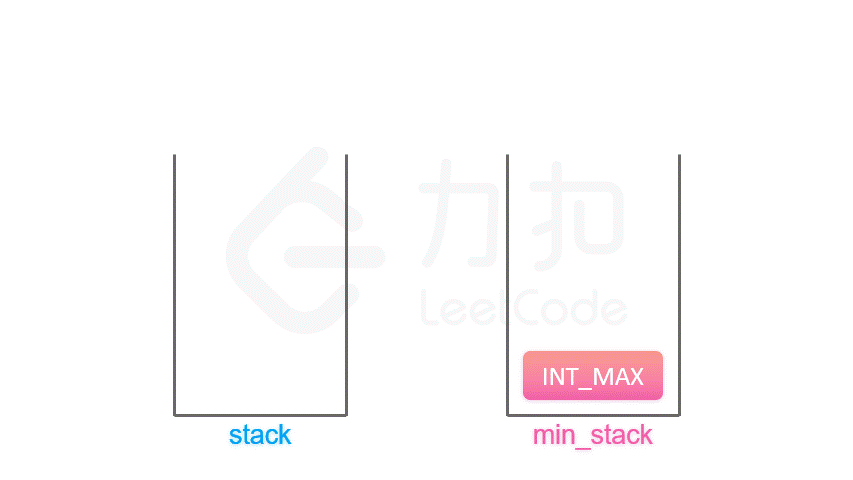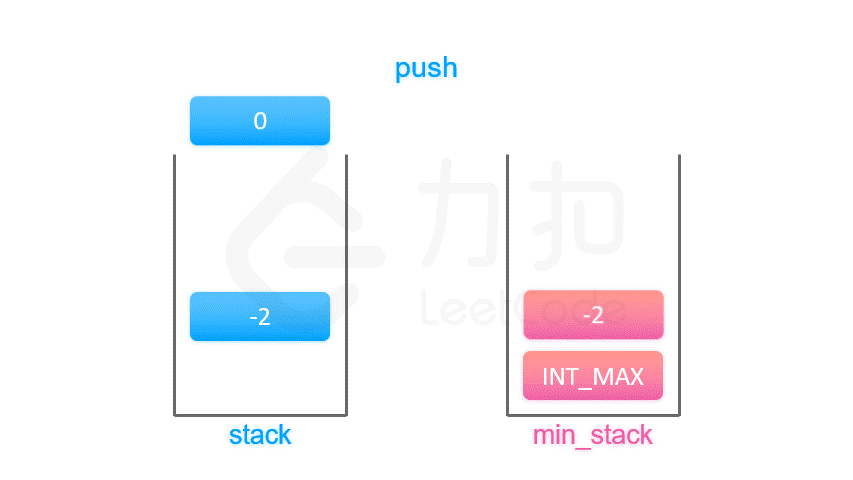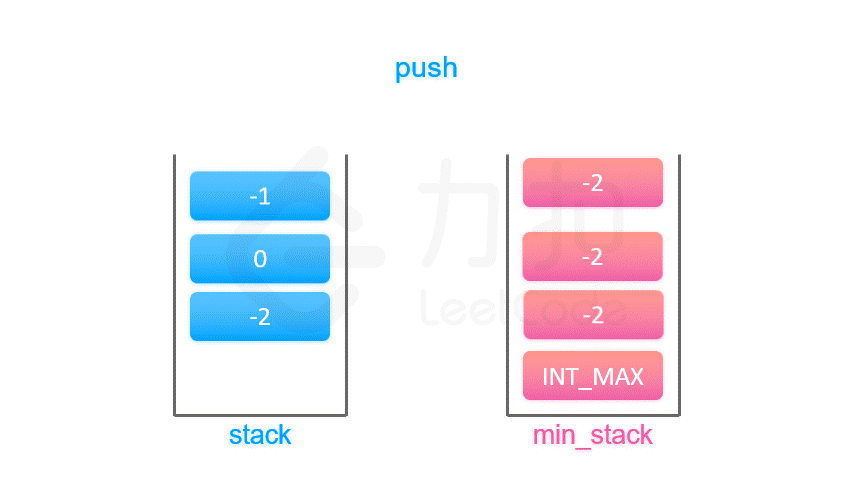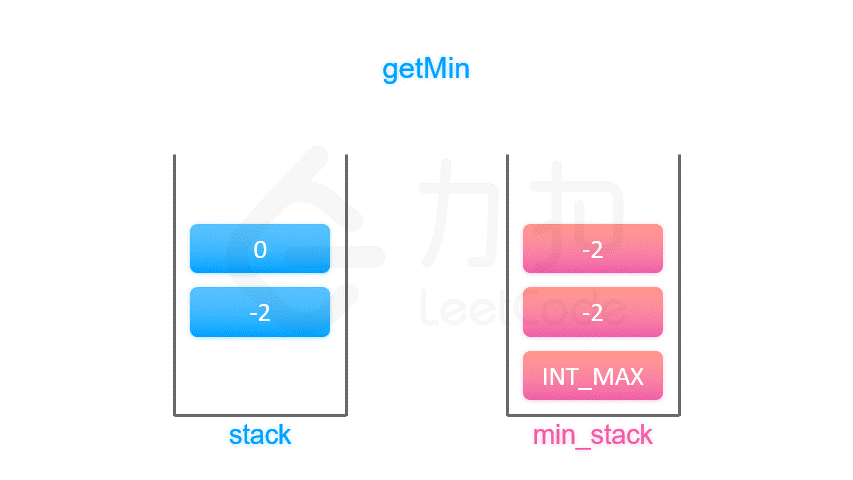
算法
按照上面的思路,我们只需要设计一个数据结构,使得每个元素 a 与其相应的最小值 m 时刻保持一一对应。因此我们可以使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
-
当一个元素要入栈时,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中;
-
当一个元素要出栈时,我们把辅助栈的栈顶元素也一并弹出;
-
在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
class MinStack {
Deque<Integer> xStack;
Deque<Integer> minStack;
public MinStack() {
xStack = new LinkedList<Integer>();
minStack = new LinkedList<Integer>();
minStack.push(Integer.MAX_VALUE);
}
public void push(int x) {
xStack.push(x);
minStack.push(Math.min(minStack.peek(), x));
}
public void pop() {
xStack.pop();
minStack.pop();
}
public int top() {
return xStack.peek();
}
public int getMin() {
return minStack.peek();
}
}
复杂度分析
-
时间复杂度:对于题目中的所有操作,时间复杂度均为 O(1)。因为栈的插入、删除与读取操作都是 O(1),我们定义的每个操作最多调用栈操作两次。
-
空间复杂度:O(n),其中 n 为总操作数。最坏情况下,我们会连续插入 n 个元素,此时两个栈占用的空间为 O(n)。
我的答案:
class MinStack {
Stack<Integer> stack;
Stack<Integer> minStack; // 辅助栈
/** initialize your data structure here. */
public MinStack() {
stack = new Stack<>();
minStack = new Stack<>();
minStack.push(Integer.MAX_VALUE);
}
public void push(int x) {
stack.push(x);
minStack.push(Math.min(minStack.peek(), x));
}
public void pop() {
stack.pop();
minStack.pop();
}
public int top() {
return stack.peek();
}
public int min() {
return minStack.peek();
}
}
/**
* Your MinStack object will be instantiated and called as such:
* MinStack obj = new MinStack();
* obj.push(x);
* obj.pop();
* int param_3 = obj.top();
* int param_4 = obj.min();
*/
剑指 Offer 31. 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如,序列 {1,2,3,4,5} 是某栈的压栈序列,序列 {4,5,3,2,1} 是该压栈序列对应的一个弹出序列,但 {4,3,5,1,2} 就不可能是该压栈序列的弹出序列。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
答案
如下图所示,给定一个压入序列 pushed 和弹出序列 popped,则压入 / 弹出操作的顺序(即排列)是 唯一确定 的。
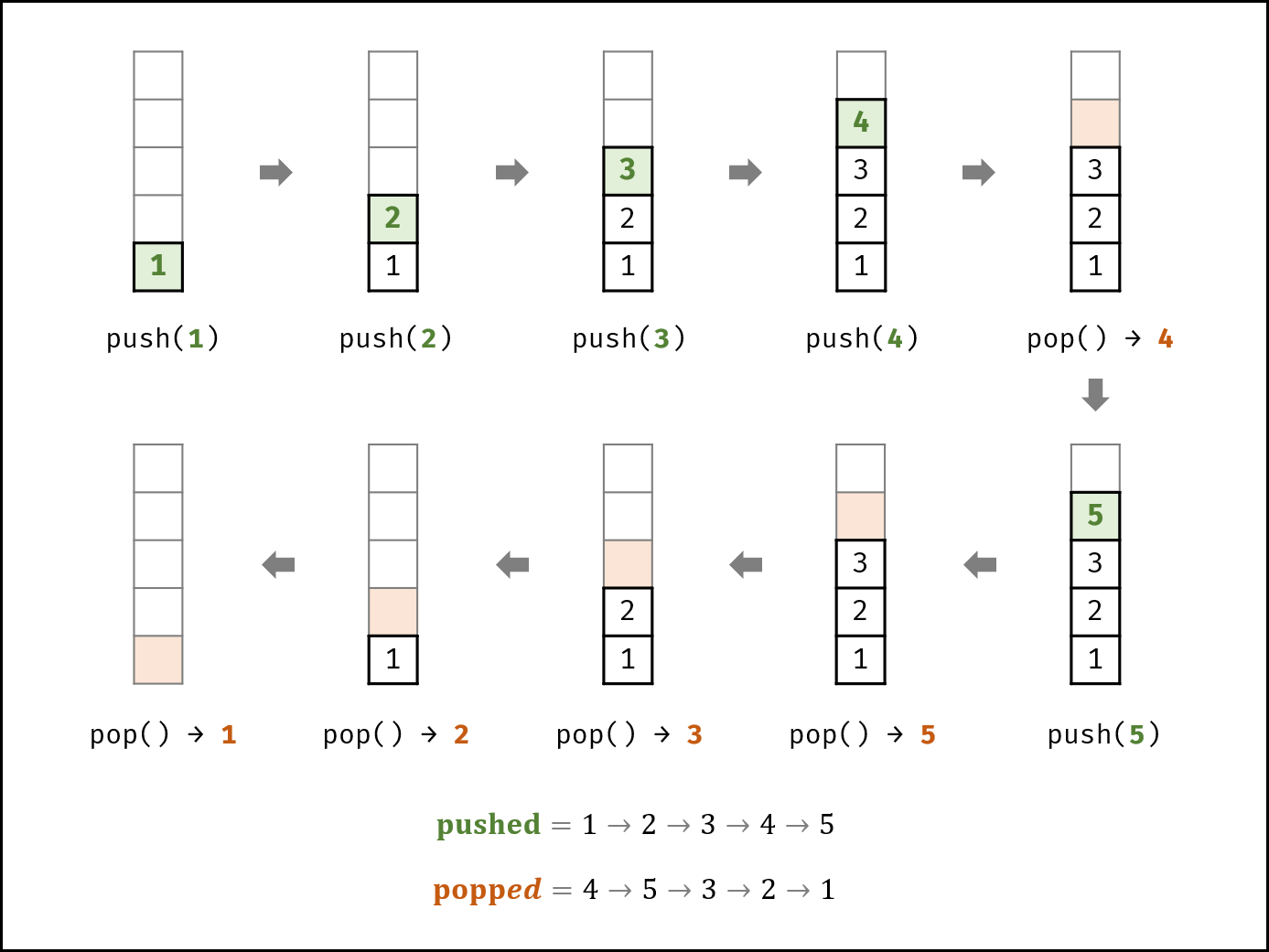
如下图所示,栈的数据操作具有 先入后出 的特性,因此某些弹出序列是无法实现的。
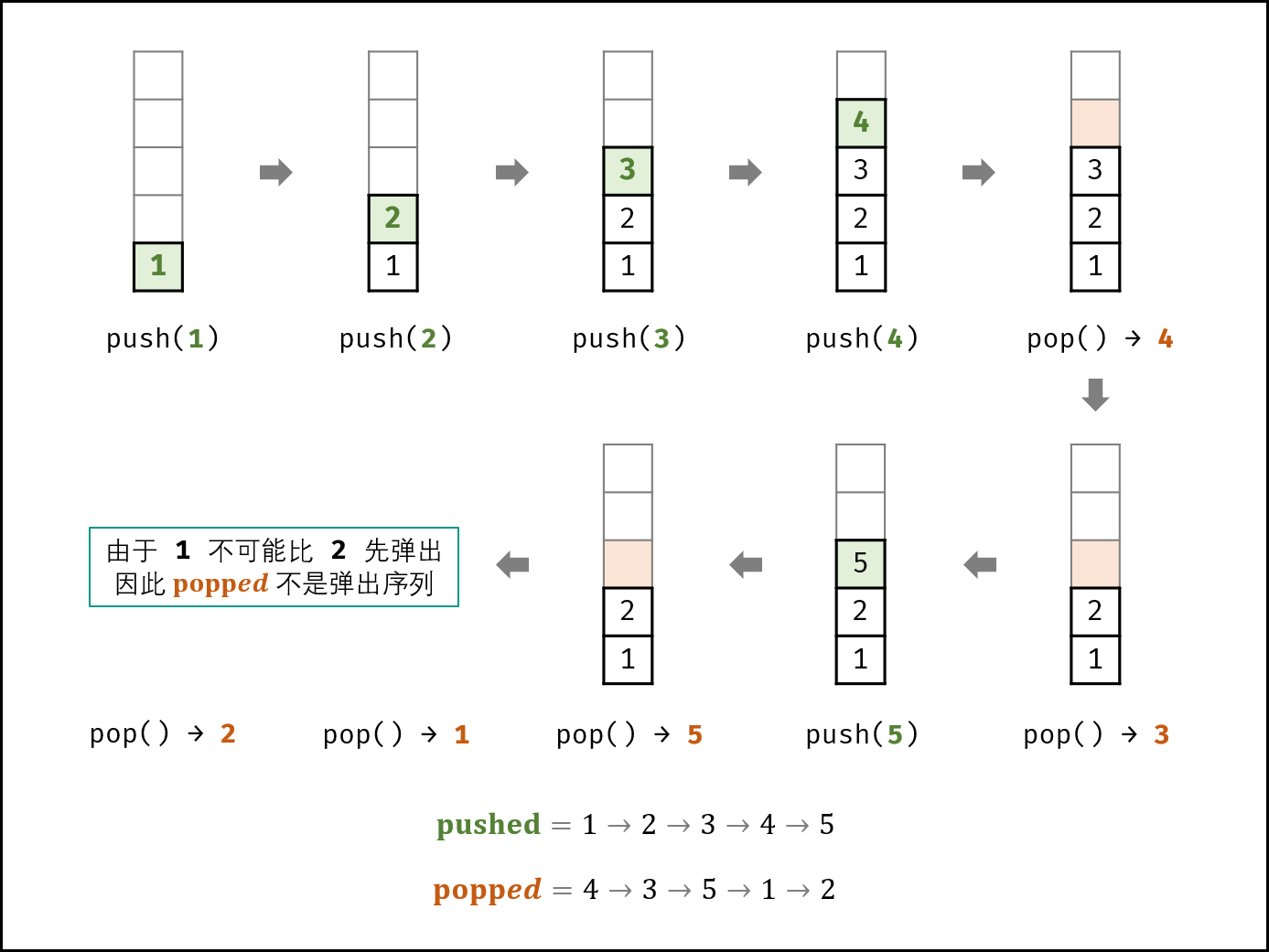
考虑借用一个辅助栈 stackstack ,模拟 压入 / 弹出操作的排列。根据是否模拟成功,即可得到结果。
- 入栈操作: 按照压栈序列的顺序执行。
- 出栈操作: 每次入栈后,循环判断 “栈顶元素 == 弹出序列的当前元素” 是否成立,将符合弹出序列顺序的栈顶元素全部弹出。
由于题目规定 栈的所有数字均不相等 ,因此在循环入栈中,每个元素出栈的位置的可能性是唯一的(若有重复数字,则具有多个可出栈的位置)。因而,在遇到 “栈顶元素 = 弹出序列的当前元素” 就应立即执行出栈。
算法流程:
- 初始化: 辅助栈 stack,弹出序列的索引 i;
- 遍历压栈序列: 各元素记为 num;
- 元素 num 入栈;
- 循环出栈:若 stack 的栈顶元素 = 弹出序列元素 popped[i] ,则执行出栈与 i++;
- 返回值: 若 stack 为空,则此弹出序列合法。
复杂度分析:
- 时间复杂度 O(N): 其中 N 为列表 pushed 的长度;每个元素最多入栈与出栈一次,即最多共 2N 次出入栈操作。
- 空间复杂度 O(N): 辅助栈 stack 最多同时存储 N 个元素。
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
int i = 0;
for(int num : pushed) {
stack.push(num); // num 入栈
while(!stack.isEmpty() && stack.peek() == popped[i]) { // 循环判断与出栈
stack.pop();
i++;
}
}
return stack.isEmpty();
}
}
我的答案:
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> s = new Stack<>();
int j = 0;
// 1. 不断地将数组压入栈
for (int i = 0; i < pushed.length; i++) {
s.push(pushed[i]);
// 2. 之后循环判断栈顶元素是否与pop数组元素一致
while (!s.isEmpty() && s.peek() == popped[j]) {
// 3. 如果一致,那就出栈
s.pop();
j++;
}
}
if (s.isEmpty()) {
return true;
}
return false;
}
}
面试题 03.05. 栈排序
栈排序。 编写程序,对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据,但不得将元素复制到别的数据结构(如数组)中。该栈支持如下操作:push、pop、peek 和 isEmpty。当栈为空时,peek 返回 -1。
示例1:
输入:
["SortedStack", "push", "push", "peek", "pop", "peek"]
[[], [1], [2], [], [], []]
输出:
[null,null,null,1,null,2]
示例2:
输入:
["SortedStack", "pop", "pop", "push", "pop", "isEmpty"]
[[], [], [], [1], [], []]
输出:
[null,null,null,null,null,true]
答案
未完待续
496. 下一个更大元素 I
nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ,找出满足 nums1[i] == nums2[j] 的下标 j ,并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素,那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
输入:nums1 = [4,1,2], nums2 = [1,3,4,2].
输出:[-1,3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 4 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
- 1 ,用加粗斜体标识,nums2 = [1,3,4,2]。下一个更大元素是 3 。
- 2 ,用加粗斜体标识,nums2 = [1,3,4,2]。不存在下一个更大元素,所以答案是 -1 。
示例 2:
输入:nums1 = [2,4], nums2 = [1,2,3,4].
输出:[3,-1]
解释:nums1 中每个值的下一个更大元素如下所述:
- 2 ,用加粗斜体标识,nums2 = [1,2,3,4]。下一个更大元素是 3 。
- 4 ,用加粗斜体标识,nums2 = [1,2,3,4]。不存在下一个更大元素,所以答案是 -1 。
方法一:暴力
思路和算法
根据题意,我们发现 \(\textit{nums}_1\) 是一个查询数组,逐个查询 \(\textit{nums}_2\) 中元素右边的第一个更大的值。因此,我们可以暴力地逐个计算 \(\textit{nums}_1\) 中的每个元素值 \(\textit{nums}_1[i]\) 在 \(\textit{nums}_2\) 中对应位置的右边的第一个比 \(\textit{nums}_1[i]\) 大的元素值。具体地,我们使用如下方法:
初始化与 \(\textit{nums}_1\) 等长的查询数组 \(\textit{res}\)。
遍历 \(\textit{nums}_1\) 中的所有元素,不妨设当前遍历到元素为 \(\textit{nums}_1[i]\):
从前向后遍历 \(\textit{nums}_2\) 中的元素,直至找到 \(\textit{nums}_2[j] = \textit{nums}_1[i]\);
从 j+1 开始继续向后遍历,直至找到 \(\textit{nums}_2[k] > \textit{nums}_2[j]\),其中 \(k \ge j+1\);
如果找到了 \(\textit{nums}_2[k]\),则将 \(\textit{res}[i]\) 置为 \(\textit{nums}_2[k]\),否则将 \(\textit{res}[i]\) 置为 −1。
查询数组 \(\textit{res}\) 即为最终结果。
代码
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
int m = nums1.length, n = nums2.length;
int[] res = new int[m];
for (int i = 0; i < m; ++i) {
int j = 0;
while (j < n && nums2[j] != nums1[i]) {
++j;
}
int k = j + 1;
while (k < n && nums2[k] < nums2[j]) {
++k;
}
res[i] = k < n ? nums2[k] : -1;
}
return res;
}
}
复杂度分析
-
时间复杂度:\(O(mn)\),其中 m 是 \(\textit{nums}_1\) 的长度,n 是 \(\textit{nums}_2\) 的长度。
-
空间复杂度:\(O(1)\)。
方法二:单调栈 + 哈希表
思路
我们可以先预处理 \(\textit{nums}_2\),使查询 \(\textit{nums}_1\) 中的每个元素在 \(\textit{nums}_2\) 中对应位置的右边的第一个更大的元素值时不需要再遍历 \(\textit{nums}_2\)。于是,我们将题目分解为两个子问题:
第 1 个子问题:如何更高效地计算 \(\textit{nums}_2\) 中每个元素右边的第一个更大的值;
第 2 个子问题:如何存储第 1 个子问题的结果。
算法
我们可以使用单调栈来解决第 1 个子问题。倒序遍历 \(\textit{nums}_2\),并用单调栈中维护当前位置右边的更大的元素列表,从栈底到栈顶的元素是单调递减的。
具体地,每次我们移动到数组中一个新的位置 i,就将当前单调栈中所有小于 \(\textit{nums}_2[i]\) 的元素弹出单调栈,当前位置右边的第一个更大的元素即为栈顶元素,如果栈为空则说明当前位置右边没有更大的元素。随后我们将位置 i 的元素入栈。
因为题目规定了 \(\textit{nums}_2\) 是没有重复元素的,所以我们可以使用哈希表来解决第 2 个子问题,将元素值与其右边第一个更大的元素值的对应关系存入哈希表。
细节
因为在这道题中我们只需要用到 \(\textit{nums}_2\) 中元素的顺序而不需要用到下标,所以栈中直接存储 \(\textit{nums}_2\) 中元素的值即可。
代码
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
Deque`<Integer>` stack = new ArrayDeque`<Integer>`();
for (int i = nums2.length - 1; i >= 0; --i) {
int num = nums2[i];
while (!stack.isEmpty() && num >= stack.peek()) {
stack.pop();
}
map.put(num, stack.isEmpty() ? -1 : stack.peek());
stack.push(num);
}
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; ++i) {
res[i] = map.get(nums1[i]);
}
return res;
}
}
复杂度分析
- 时间复杂度:\(O(m + n)\),其中 m 是 \(\textit{nums}_1\) 的长度,n 是 \(\textit{nums}_2\) 的长度。我们需要遍历 \(\textit{nums}_2\) 以计算 \(\textit{nums}_2\) 中每个元素右边的第一个更大的值;需要遍历 \(\textit{nums}_1\) 以生成查询结果。
- 空间复杂度:\(O(n)\),用于存储哈希表。
我的
class Solution {
public int[] nextGreaterElement(int[] nums1, int[] nums2) {
// 单调递减栈
Deque<Integer> stack = new LinkedList<>();
Map<Integer, Integer> map = new HashMap<>();
for (int num : nums2) {
while (!stack.isEmpty() && num > stack.peek()) {
int top = stack.pop();
// 查找右侧比当前元素大的,看 「 弹出栈 」 时即将插入的元素。
map.put(top, num);
}
stack.push(num);
}
while (!stack.isEmpty()) {
map.put(stack.pop(), -1);
}
int[] res = new int[nums1.length];
for (int i = 0; i < nums1.length; ++i) {
res[i] = map.get(nums1[i]);
}
return res;
}
}
739. 每日温度
给定一个整数数组 temperatures ,表示每天的温度,返回一个数组 answer ,其中 answer[i] 是指对于第 i 天,下一个更高温度出现在几天后。如果气温在这之后都不会升高,请在该位置用 0 来代替。
示例 1:
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]
示例 2:
输入: temperatures = [30,40,50,60]
输出: [1,1,1,0]
示例 3:
输入: temperatures = [30,60,90]
输出: [1,1,0]
方法一:暴力
对于温度列表中的每个元素 temperatures[i],需要找到最小的下标 j,使得 i < j 且 temperatures[i] < temperatures[j]。
由于温度范围在 [30, 100] 之内,因此可以维护一个数组 next 记录每个温度第一次出现的下标。数组 next 中的元素初始化为无穷大,在遍历温度列表的过程中更新 next 的值。
反向遍历温度列表。对于每个元素 temperatures[i],在数组 next 中找到从 temperatures[i] + 1 到 100 中每个温度第一次出现的下标,将其中的最小下标记为 warmerIndex,则 warmerIndex 为下一次温度比当天高的下标。如果 warmerIndex 不为无穷大,则 warmerIndex - i 即为下一次温度比当天高的等待天数,最后令 next[temperatures[i]] = i。
为什么上述做法可以保证正确呢?因为遍历温度列表的方向是反向,当遍历到元素 temperatures[i] 时,只有 temperatures[i] 后面的元素被访问过,即对于任意 t,当 next[t] 不为无穷大时,一定存在 j 使得 temperatures[j] == t 且 i < j。又由于遍历到温度列表中的每个元素时都会更新数组 next 中的对应温度的元素值,因此对于任意 t,当 next[t] 不为无穷大时,令 j = next[t],则 j 是满足 temperatures[j] == t 且 i < j 的最小下标。
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int length = temperatures.length;
int[] ans = new int[length];
int[] next = new int[101];
Arrays.fill(next, Integer.MAX_VALUE);
for (int i = length - 1; i >= 0; --i) {
int warmerIndex = Integer.MAX_VALUE;
for (int t = temperatures[i] + 1; t <= 100; ++t) {
if (next[t] < warmerIndex) {
warmerIndex = next[t];
}
}
if (warmerIndex < Integer.MAX_VALUE) {
ans[i] = warmerIndex - i;
}
next[temperatures[i]] = i;
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(nm)\),其中 n 是温度列表的长度,m 是数组 next 的长度,在本题中温度不超过 100,所以 m 的值为 100。反向遍历温度列表一遍,对于温度列表中的每个值,都要遍历数组 next 一遍。
-
空间复杂度:\(O(m)\),其中 m 是数组 next 的长度。除了返回值以外,需要维护长度为 m 的数组 next 记录每个温度第一次出现的下标位置。
方法二:单调栈
可以维护一个存储下标的单调栈,从栈底到栈顶的下标对应的温度列表中的温度依次递减。如果一个下标在单调栈里,则表示尚未找到下一次温度更高的下标。
正向遍历温度列表。对于温度列表中的每个元素 temperatures[i],如果栈为空,则直接将 i 进栈,如果栈不为空,则比较栈顶元素 prevIndex 对应的温度 temperatures[prevIndex] 和当前温度 temperatures[i],如果 temperatures[i] > temperatures[prevIndex],则将 prevIndex 移除,并将 prevIndex 对应的等待天数赋为 i - prevIndex,重复上述操作直到栈为空或者栈顶元素对应的温度小于等于当前温度,然后将 i 进栈。
为什么可以在弹栈的时候更新 ans[prevIndex] 呢?因为在这种情况下,即将进栈的 i 对应的 temperatures[i] 一定是 temperatures[prevIndex] 右边第一个比它大的元素,试想如果 prevIndex 和 i 有比它大的元素,假设下标为 j,那么 prevIndex 一定会在下标 j 的那一轮被弹掉。
由于单调栈满足从栈底到栈顶元素对应的温度递减,因此每次有元素进栈时,会将温度更低的元素全部移除,并更新出栈元素对应的等待天数,这样可以确保等待天数一定是最小的。
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int length = temperatures.length;
int[] ans = new int[length];
Deque<Integer> stack = new LinkedList<Integer>();
for (int i = 0; i < length; i++) {
int temperature = temperatures[i];
while (!stack.isEmpty() && temperature > temperatures[stack.peek()]) {
int prevIndex = stack.pop();
ans[prevIndex] = i - prevIndex;
}
stack.push(i);
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是温度列表的长度。正向遍历温度列表一遍,对于温度列表中的每个下标,最多有一次进栈和出栈的操作。
-
空间复杂度:\(O(n)\),其中 n 是温度列表的长度。需要维护一个单调栈存储温度列表中的下标。
42. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
单调栈
除了计算并存储每个位置两边的最大高度以外,也可以用单调栈计算能接的雨水总量。
维护一个单调栈,单调栈存储的是下标,满足从栈底到栈顶的下标对应的数组 \(\textit{height}\) 中的元素递减。
从左到右遍历数组,遍历到下标 ii 时,如果栈内至少有两个元素,记栈顶元素为 \(\textit{top}\),\(\textit{top}\) 的下面一个元素是 \(\textit{left}\),则一定有 \(\textit{height}[\textit{left}] \ge \textit{height}[\textit{top}]\)。如果 \(\textit{height}[i]>\textit{height}[\textit{top}]\),则得到一个可以接雨水的区域,该区域的宽度是 \(i-\textit{left}-1\),高度是 \(\min(\textit{height}[\textit{left}],\textit{height}[i])-\textit{height}[\textit{top}]\),根据宽度和高度即可计算得到该区域能接的雨水量。
为了得到 \(\textit{left}\),需要将 \(\textit{top}\) 出栈。在对 \(\textit{top}\) 计算能接的雨水量之后,\textit{left}left 变成新的 \(\textit{top}\),重复上述操作,直到栈变为空,或者栈顶下标对应的 \(\textit{height}\) 中的元素大于或等于 \(\textit{height}[i]\)。
在对下标 i 处计算能接的雨水量之后,将 i 入栈,继续遍历后面的下标,计算能接的雨水量。遍历结束之后即可得到能接的雨水总量。
class Solution {
public int trap(int[] height) {
int ans = 0;
Deque<Integer> stack = new LinkedList<Integer>();
int n = height.length;
for (int i = 0; i < n; ++i) {
while (!stack.isEmpty() && height[i] > height[stack.peek()]) {
int top = stack.pop();
if (stack.isEmpty()) {
break;
}
int left = stack.peek();
int currWidth = i - left - 1;
int currHeight = Math.min(height[left], height[i]) - height[top];
ans += currWidth * currHeight;
}
stack.push(i);
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{height}\) 的长度。从 0 到 n-1 的每个下标最多只会入栈和出栈各一次。
-
空间复杂度:\(O(n)\),其中 n 是数组 \(\textit{height}\) 的长度。空间复杂度主要取决于栈空间,栈的大小不会超过 n。
962. 最大宽度坡
给定一个整数数组 A,坡是元组 (i, j),其中 i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。
找出 A 中的坡的最大宽度,如果不存在,返回 0 。
示例 1:
输入:[6,0,8,2,1,5]
输出:4
解释:
最大宽度的坡为 (i, j) = (1, 5): A[1] = 0 且 A[5] = 5.
示例 2:
输入:[9,8,1,0,1,9,4,0,4,1]
输出:7
解释:
最大宽度的坡为 (i, j) = (2, 9): A[2] = 1 且 A[9] = 1.
我的
首先正序遍历数组 A,将以 A[0] 开始的递减序列的元素下标依次存入栈中。
为什么要存从 A[0] 开始的递减序列呢?
因为题中条件 A[i] <= A[j],所以要让 A[i] 的值尽可能的小,即从 A[0] 开始的一个递减序列。单调栈中记录的是从后往前每个大分段 “坡底” 所在的位置。
以 [6, 1, 8, 2, 0, 5] 为例,由于 (6, 1, 0) 是递减的,所以栈中存的元素应该为:(栈顶 -> (4, 1, 0) <- 栈底)。
其中 [2, 0, 5] 也是一个满足条件的坡并且宽度为 2,但是为什么在计算的时候没有算它呢?
因为该数组从 A[0] 开始的递减序列为 (6, 1, 0) 并没有元素 2,是因为在元素 2 的左边有比它还要小的元素 1。当计算最大宽度坡时 1 和 2 相比,不管是元素值还是元素的下标都更小,所以若以 2 为坡底能计算出某一坡的宽度时同样的以 1 为坡底也能计算出相应的坡的宽度并且宽度更大,所以就不需要计算以 2 为坡底的坡的宽度了。
此时栈 stack:(4(0), 1(1), 0(6)):然后逆序遍历数组 A,若以栈顶元素为下标的元素值 A[stack.peek()] 小于等于当前遍历的元素 A[i],即 A[stack.peek()] <= A[i]。此时就是一个满足条件的坡的宽度,并且这个宽度一定是栈顶这个坡底 i 能形成的最大宽度,将栈顶元素出栈并计算当前坡的宽度,保留最大值即可。
while (!stack.isEmpty() && A[stack.peek()] <= A[i]) {
int pos = stack.pop();
maxWidth = Math.max(maxWidth, i - pos);
}
最后返回最大宽坡度即可。
代码
class Solution {
public int maxWidthRamp(int[] A) {
int n = A.length;
int maxWidth = 0;
Stack<Integer> stack = new Stack<>();
for (int i=0;i<n;i++) {
if (stack.isEmpty() || A[stack.peek()] > A[i]) {
stack.push(i);
}
}
for (int i=n-1;i>=0;i--) {
while (!stack.isEmpty() && A[stack.peek()] <= A[i]) {
int pos = stack.pop();
maxWidth = Math.max(maxWidth, i - pos);
}
}
return maxWidth;
}
}
复杂度:
- 时间复杂度:O(n)
- 空间复杂度:O(n)
901. 股票价格跨度
编写一个 StockSpanner 类,它收集某些股票的每日报价,并返回该股票当日价格的跨度。
今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数(从今天开始往回数,包括今天)。
例如,如果未来7天股票的价格是 [100, 80, 60, 70, 60, 75, 85],那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。
示例:
输入:["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
输出:[null,1,1,1,2,1,4,6]
解释:
首先,初始化 S = StockSpanner(),然后:
S.next(100) 被调用并返回 1,
S.next(80) 被调用并返回 1,
S.next(60) 被调用并返回 1,
S.next(70) 被调用并返回 2,
S.next(60) 被调用并返回 1,
S.next(75) 被调用并返回 4,
S.next(85) 被调用并返回 6。
注意 (例如) S.next(75) 返回 4,因为截至今天的最后 4 个价格
(包括今天的价格 75) 小于或等于今天的价格。
单调栈
分析
求出小于或等于今天价格的最大连续日数等价于求出最近的一个大于今日价格的日子。如果第 i 天的价格为 A[i],第 j 天的价格为 A[j],满足 i < j 且 A[i] <= A[j],那么在第 j 天之后,第 i 天不会是任何一天询问的答案,因为如果对于第 k, k > j 天而言,第 i 天是最近的一个大于今日价格的日子,但第 j 天出现在第 i 天之后且价格不低于第 i 天,因此出现了矛盾。
有了这样一个结论,我们只需要维护一个单调递减的序列,称之为”单调栈“。例如股票每天的价格为 [11, 3, 9, 5, 6, 4],那么每天结束之后,对应的单调栈分别为:
[11]
[11, 3]
[11, 9]
[11, 9, 5]
[11, 9, 6]
[11, 9, 6, 4]
当我们得到了新的一天的价格(例如 7)时,我们将栈中所有小于等于 7 的元素全部取出,因为根据之前的结论,这些元素不会成为后续询问的答案。当栈顶的元素大于 7 时,我们就得到最近的一个大于 7 的价格为 9。
算法
我们用单调栈维护一个单调递减的价格序列,并且对于每个价格,存储一个 weight 表示它离上一个价格之间(即最近的一个大于它的价格之间)的天数。如果是栈底的价格,则存储它本身对应的天数。例如 [11, 3, 9, 5, 6, 4, 7] 对应的单调栈为 (11, weight=1), (9, weight=2), (7, weight=4)。
当我们得到了新的一天的价格,例如 10,我们将所有栈中所有小于等于 10 的元素全部取出,将它们的 weight 进行累加,再加上 1 就得到了答案。在这之后,我们把 10 和它对应的 weight 放入栈中,得到 (11, weight=1), (10, weight=7)。
class StockSpanner {
Stack<Integer> prices, weights;
public StockSpanner() {
prices = new Stack();
weights = new Stack();
}
public int next(int price) {
int w = 1;
while (!prices.isEmpty() && prices.peek() <= price) {
prices.pop();
w += weights.pop();
}
prices.push(price);
weights.push(w);
return w;
}
}
复杂度分析
-
时间复杂度:\(O(Q)\),其中 Q 是调用 next() 函数的次数。
-
空间复杂度:\(O(Q)\)。
1124. 表现良好的最长时间段
给你一份工作时间表 hours,上面记录着某一位员工每天的工作小时数。
我们认为当员工一天中的工作小时数大于 8 小时的时候,那么这一天就是「劳累的一天」。
所谓「表现良好的时间段」,意味在这段时间内,「劳累的天数」是严格 大于「不劳累的天数」。
请你返回「表现良好时间段」的最大长度。
示例 1:
输入:hours = [9,9,6,0,6,6,9]
输出:3
解释:最长的表现良好时间段是 [9,9,6]。
示例 2:
输入:hours = [6,6,6]
输出:0
单调栈
思路和算法
数组 \(\textit{hours}\) 的每个子数组对应一个时间段。如果一个子数组中的大于 8 的元素个数严格超过小于等于 8 的元素个数,则该子数组对应的时间段是表现良好的时间段。
为了方便计算,可以将每天的工作小时数转换成得分,大于 8 小时对应得分 1,小于等于 8 小时对应得分 -1。将工作小时数转换成得分以后,表现良好的时间段等价于元素和大于 0 的子数组。
对于长度为 n 的数组 \(\textit{hours}\),将工作小时数转换成得分以后,计算得分数组的前缀和数组。前缀和数组 \(\textit{sums}\) 的长度为 n + 1,对于 \(0 \le i \le n\),\(\textit{sums}[i]\) 表示得分数组的前 i 个得分之和。
假设存在两个下标 i 和 j 满足 \(0 \le i < j \le n\),则得分数组的下标范围 \([i, j - 1]\) 的子数组的得分之和为 \(\textit{sums}[j] - \textit{sums}[i]\),该子数组的长度是 \(j - i\)。如果 \(\textit{sums}[j] - \textit{sums}[i] > 0\) 即 \(\textit{sums}[i] < \textit{sums}[j]\),则存在一个长度为 \(j - i\) 的表现良好的时间段。
考虑表现良好的时间段 \([i, j - 1]\),有 \(\textit{sums}[i] < \textit{sums}[j]\)。对于下标 \(k < i\),如果 \(\textit{sums}[k] \le \textit{sums}[i]\),则必有 \(\textit{sums}[k] < \textit{sums}[j]\),因此得分数组的下标范围 \([k, j - 1]\) 的子数组对应的时间段也是表现良好的时间段,且该时间段的长度 \(j - k\) 大于 \(j - i\)。因此,只有当任意小于 i 的下标 k 都满足 \(\textit{sums}[k] > \textit{sums}[i]\) 时,下标 i 才可能是表现良好的最长时间段的开始下标。根据该结论,可以排除不可能是表现良好的最长时间段的开始下标的下标。以下用「时间段」表示表现良好的时间段,用「最长时间段」表示表现良好的最长时间段。
可以使用单调栈存储可能是最长时间段的开始下标的全部下标,单调栈满足从栈底到栈顶的下标对应的 \(\textit{sums}\) 的元素单调递减。
从左到右遍历数组 \(\textit{sums}\),对于每个下标 i,当且仅当栈为空或者栈顶下标对应的元素大于 \(\textit{sums}[i]\) 时,将 i 入栈。遍历结束之后,栈内的每个下标 i 都满足对于任意小于 i 的下标 k 都有 \(\textit{sums}[k] > \textit{sums}[i]\)。
然后从右到左遍历数组 \(\textit{sums}\),对于每个下标 j,需要找到最小的下标 i 使得 \(\textit{sums}[i] < \textit{sums}[j]\)。具体做法是,当栈不为空且栈顶下标对应的元素小于 \(\textit{sums}[j]\) 时,令栈顶下标为 i,将 i 出栈,并用 \(j - i\) 更新最长时间段,重复该操作直到栈为空或者栈顶下标对应的元素大于 \(\textit{sums}[j]\)。该做法的正确性说明如下。
-
对于下标 j,如果有多个小于 j 的下标对应的元素都小于 \(\textit{sums}[j]\),则其中最小的下标和 j 组成以 j 结尾的最长时间段。由于单调栈的下标入栈顺序为下标递增顺序,因此越接近栈底的下标越小,和 j 组成的时间段也越长。为了得到以下标 j 结尾的最长时间段,应在栈内找到最小的下标 i 使得 \(\textit{sums}[i] < \textit{sums}[j]\),因此应该将全部满足 \(\textit{sums}[i] < \textit{sums}[j]\) 的下标 i 出栈,在出栈的同时更新最长时间段。
-
假设存在下标 k 满足 \(k < j\) 且 \(\textit{sums}[k] \le \textit{sums}[j]\),则任何以 k 结尾的时间段的开始下标都可以是以 j 结尾的时间段的开始下标,因此以 k 结尾的最长时间段一定小于以 j 结尾的最长时间段。
-
假设存在下标 k 满足 \(k < j\) 且 \(\textit{sums}[k] > \textit{sums}[j]\),则可能存在下标 p 满足 \(p < k\) 且 \(\textit{sums}[j] \le \textit{sums}[p] < \textit{sums}[k]\),此时下标 p 可以是以 k 结尾的时间段的开始下标,但是不可以是以 j 结尾的时间段的开始下标。在遍历到 k 时,计算以 k 结尾的最长时间段一定会将 p 出栈。
代码
Java
class Solution {
public int longestWPI(int[] hours) {
int maxInterval = 0;
int n = hours.length;
int[] sums = new int[n + 1];
for (int i = 0; i < n; i++) {
int score = hours[i] > 8 ? 1 : -1;
sums[i + 1] = sums[i] + score;
}
Deque<Integer> stack = new ArrayDeque<Integer>();
for (int i = 0; i <= n; i++) {
int sum = sums[i];
if (stack.isEmpty() || sums[stack.peek()] > sum) {
stack.push(i);
}
}
for (int j = n; j >= 0; j--) {
int sum = sums[j];
while (!stack.isEmpty() && sums[stack.peek()] < sum) {
int interval = j - stack.pop();
maxInterval = Math.max(maxInterval, interval);
}
}
return maxInterval;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是数组 hours 的长度。计算前缀和数组需要 \(O(n)\) 的时间,得到前缀和数组之后,需要从左到右遍历前缀和数组将下标入单调栈,然后从右到左遍历数前缀和数组计算表现良好的最长时间段。由于每个下标最多入栈和出栈各一次,因此时间复杂度是 \(O(n)\)。
-
空间复杂度:\(O(n)\),其中 n 是数组 hours 的长度。空间复杂度主要取决于前缀和数组与栈的空间,前缀和数组的长度是 n + 1,栈内元素个数不会超过 n + 1。
前缀和+哈希表
思路和算法
这道题也可以使用前缀和与哈希表的做法解决,哈希表中记录每个非零前缀和的第一次出现的下标。
将前缀和记为 sum。从左到右遍历数组 hours,对于每个下标 i,执行以下操作。
-
如果 hours[i]>8,则将 sum 加 1,否则将 sum 减 1。
-
根据 sum 更新表现良好的最长时间段。
-
如果 sum>0,则以下标 i 结尾的前缀为表现良好的时间段,其长度为 i + 1,用 i + 1 更新表现良好的最长时间段。
-
如果sum≤0 且哈希表中存在前缀和 sum−1,则从哈希表中获得前缀和 sum−1 的第一次出现的下标 j,下标范围 [j + 1, i] 的子数组对应的时间段为表现良好的时间段,其长度为 i - j,用 i - j 更新表现良好的最长时间段。
-
如果哈希表中不存在前缀和 sum,则将前缀和 sum 对应下标 i 存入哈希表。
-
遍历结束之后,即可得到表现良好的最长时间段。
该做法的正确性说明如下。
当遍历到下标 i 时,如果 sum>0,则以下标 i 结尾的最长子数组的长度为 i + 1,该子数组为表现良好的时间段。不存在以下标 i 结尾且长度大于 i + 1 的子数组。
假设 x 和 y 都是数组的前缀和,且 y < x < 0。由于计算前缀和时每次将前缀和加 1 或减 1,因此在前缀和首次变成 y 之前,前缀和一定会经过 -1 到 y + 1 的每个整数。由于 y+1≤x≤−1,因此在前缀和首次变成 y 之前,前缀和一定会经过 x,即前缀和 x 的第一次出现的下标一定小于前缀和 y 的第一次出现的下标。当遍历到下标 i 时,如果 sum≥0 且存在以 i 结尾的表现良好的时间段,只需要考虑前缀和 sum−1 的第一次出现的下标 jj,则以 ii 结尾的表现良好的最长时间段的长度一定是 i - j,任何小于 sum−1 的前缀和如果存在则第一次出现的下标一定大于 j。
代码
Java
class Solution {
public int longestWPI(int[] hours) {
int maxInterval = 0;
Map<Integer, Integer> indices = new HashMap<Integer, Integer>();
int sum = 0;
int n = hours.length;
for (int i = 0; i < n; i++) {
int score = hours[i] > 8 ? 1 : -1;
sum += score;
if (sum > 0) {
maxInterval = Math.max(maxInterval, i + 1);
} else if (indices.containsKey(sum - 1)) {
int interval = i - indices.get(sum - 1);
maxInterval = Math.max(maxInterval, interval);
}
indices.putIfAbsent(sum, i);
}
return maxInterval;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{hours}\) 的长度。需要遍历数组 \(\textit{hours}\) 一次,对于每个元素计算前缀和、表现良好的最长时间段以及更新哈希表的时间都是 \(O(1)\)。
-
空间复杂度:\(O(n)\),其中 n 是数组 \(\textit{hours}\) 的长度。空间复杂度主要取决于哈希表空间,哈希表中的元素个数不会超过 n。
316. 去除重复字母
给你一个字符串 s ,请你去除字符串中重复的字母,使得每个字母只出现一次。需保证 返回结果的字典序最小(要求不能打乱其他字符的相对位置)。
示例 1:
输入:s = "bcabc"
输出:"abc"
示例 2:
输入:s = "cbacdcbc"
输出:"acdb"
贪心 + 单调栈
思路与算法
首先考虑一个简单的问题:给定一个字符串 s,如何去掉其中的一个字符 ch,使得得到的字符串字典序最小呢?答案是:找出最小的满足 s[i]>s[i+1] 的下标 i,并去除字符 s[i]。为了叙述方便,下文中称这样的字符为「关键字符」。
在理解这一点之后,就可以着手本题了。一个直观的思路是:我们在字符串 s 中找到「关键字符」,去除它,然后不断进行这样的循环。但是这种朴素的解法会创建大量的中间字符串,我们有必要寻找一种更优的方法。
我们从前向后扫描原字符串。每扫描到一个位置,我们就尽可能地处理所有的「关键字符」。假定在扫描位置 s[i-1] 之前的所有「关键字符」都已经被去除完毕,在扫描字符 s[i] 时,新出现的「关键字符」只可能出现在 s[i] 或者其后面的位置。
于是,我们使用单调栈来维护去除「关键字符」后得到的字符串,单调栈满足栈底到栈顶的字符递增。如果栈顶字符大于当前字符 s[i],说明栈顶字符为「关键字符」,故应当被去除。去除后,新的栈顶字符就与 s[i] 相邻了,我们继续比较新的栈顶字符与 s[i] 的大小。重复上述操作,直到栈为空或者栈顶字符不大于 s[i]。
我们还遗漏了一个要求:原字符串 s 中的每个字符都需要出现在新字符串中,且只能出现一次。为了让新字符串满足该要求,之前讨论的算法需要进行以下两点的更改。
-
在考虑字符 s[i] 时,如果它已经存在于栈中,则不能加入字符 s[i]。为此,需要记录每个字符是否出现在栈中。
-
在弹出栈顶字符时,如果字符串在后面的位置上再也没有这一字符,则不能弹出栈顶字符。为此,需要记录每个字符的剩余数量,当这个值为 0 时,就不能弹出栈顶字符了。
代码
class Solution {
public String removeDuplicateLetters(String s) {
boolean[] vis = new boolean[26];
int[] num = new int[26];
for (int i = 0; i < s.length(); i++) {
num[s.charAt(i) - 'a']++;
}
StringBuffer sb = new StringBuffer();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (!vis[ch - 'a']) {
while (sb.length() > 0 && sb.charAt(sb.length() - 1) > ch) {
if (num[sb.charAt(sb.length() - 1) - 'a'] > 0) {
vis[sb.charAt(sb.length() - 1) - 'a'] = false;
sb.deleteCharAt(sb.length() - 1);
} else {
break;
}
}
vis[ch - 'a'] = true;
sb.append(ch);
}
num[ch - 'a'] -= 1;
}
return sb.toString();
}
}
复杂度分析
-
时间复杂度:\(O(N)\),其中 N 为字符串长度。代码中虽然有双重循环,但是每个字符至多只会入栈、出栈各一次。
-
空间复杂度:\(O(|\Sigma|)\),其中 \(\Sigma\) 为字符集合,本题中字符均为小写字母,所以 \(|\Sigma|=26\)。由于栈中的字符不能重复,因此栈中最多只能有 \(|\Sigma|\) 个字符,另外需要维护两个数组,分别记录每个字符是否出现在栈中以及每个字符的剩余数量。
我的
class Solution {
public String removeDuplicateLetters(String s) {
Deque<Character> stack = new LinkedList<>();
boolean[] vis = new boolean[26];
int[] map = new int[26];
for (int i = 0; i < s.length(); i++) {
char cur = s.charAt(i);
map[cur - 'a']++;
}
for (int i = 0; i < s.length(); i++) {
char cur = s.charAt(i);
if (!stack.contains(cur)) {
if (stack.isEmpty() || cur > stack.peek()) {
map[cur - 'a']--;
stack.push(cur);
} else {
if (map[stack.peek() - 'a'] > 0) {
stack.pop();
i--;
} else if (!stack.contains(cur)) { // 如果栈顶元素是最后一个,弹不出来,那就加一下当前元素
map[cur - 'a']--;
stack.push(cur);
}
}
} else {
map[cur - 'a']--;
}
}
StringBuilder sb = new StringBuilder();
while (!stack.isEmpty()) {
sb.append(stack.pop());
}
return sb.reverse().toString();
}
}
[84. 柱状图中最大的矩形]
946. 验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true;否则,返回 false 。
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
答案
方法一: 贪心
思路
所有的元素一定是按顺序 push 进去的,重要的是怎么 pop 出来?
假设当前栈顶元素值为 2,同时对应的 popped 序列中下一个要 pop 的值也为 2,那就必须立刻把这个值 pop 出来。因为之后的 push 都会让栈顶元素变成不同于 2 的其他值,这样再 pop 出来的数 popped 序列就不对应了。
算法
将 pushed 队列中的每个数都 push 到栈中,同时检查这个数是不是 popped 序列中下一个要 pop 的值,如果是就把它 pop 出来。
最后,检查不是所有的该 pop 出来的值都是 pop 出来了。
class Solution {
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
int cur = 0;
for (int i = 0; i < pushed.length; i++) {
stack.push(pushed[i]);
while (!stack.isEmpty() && stack.peek() == popped[cur]) {
stack.pop();
cur++;
}
}
return cur > popped.length - 1;
}
}
算法复杂度
- 时间复杂度:\(O(N)\),其中 N 是 pushed 序列和 popped 序列的长度。
- 空间复杂度:\(O(N)\)。
队列的相关算法
225. 用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
实现 MyStack 类:
- void push(int x) 将元素 x 压入栈顶。
- int pop() 移除并返回栈顶元素。
- int top() 返回栈顶元素。
- boolean empty() 如果栈是空的,返回 true ;否则,返回 false 。
注意:
- 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
- 你所使用的语言也许不支持队列。 你可以使用 list (列表)或者 deque(双端队列)来模拟一个队列 , 只要是标准的队列操作即可。
示例:
输入:
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出:
[null, null, null, 2, 2, false]
解释:
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False
双队列
双队列:将队列逆置
- 入栈:把队列中的元素出队,将当前元素入队,再将之前的队列元素入队
- 出栈:正常出队即可
方法一:两个队列
为了满足栈的特性,即最后入栈的元素最先出栈,在使用队列实现栈时,应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作,其中 \(\textit{queue}_1\) 用于存储栈内的元素,\(\textit{queue}_2\) 作为入栈操作的辅助队列。
入栈操作时,首先将元素入队到 \(\textit{queue}_2\),然后将 \(\textit{queue}_1\) 的全部元素依次出队并入队到 \(\textit{queue}_2\),此时 \(\textit{queue}_2\) 的前端的元素即为新入栈的元素,再将 \(\textit{queue}_1\) 和 \(\textit{queue}_2\) 互换,则 \(\textit{queue}_1\) 的元素即为栈内的元素,\(\textit{queue}_1\) 的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保 \(\textit{queue}_1\) 的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 \(\textit{queue}_1\) 的前端元素并返回即可,获得栈顶元素操作只需要获得 \(\textit{queue}_1\) 的前端元素并返回即可(不移除元素)。
由于 \(\textit{queue}_1\) 用于存储栈内的元素,判断栈是否为空时,只需要判断 \(\textit{queue}_1\) 是否为空即可。

class MyStack {
Queue<Integer> queue1;
Queue<Integer> queue2;
/** Initialize your data structure here. */
public MyStack() {
queue1 = new LinkedList<Integer>();
queue2 = new LinkedList<Integer>();
}
/** Push element x onto stack. */
public void push(int x) {
queue2.offer(x);
while (!queue1.isEmpty()) {
queue2.offer(queue1.poll());
}
Queue<Integer> temp = queue1;
queue1 = queue2;
queue2 = temp;
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue1.poll();
}
/** Get the top element. */
public int top() {
return queue1.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue1.isEmpty();
}
}
复杂度分析
-
时间复杂度:入栈操作 \(O(n)\),其余操作都是 \(O(1)\),其中 n 是栈内的元素个数。
入栈操作需要将 \(\textit{queue}_1\) 中的 n 个元素出队,并入队 \(n+1\) 个元素到 \(\textit{queue}_2\),共有 \(2n+1\) 次操作,每次出队和入队操作的时间复杂度都是 \(O(1)\),因此入栈操作的时间复杂度是 \(O(n)\)。
出栈操作对应将 \(\textit{queue}_1\) 的前端元素出队,时间复杂度是 \(O(1)\)。
获得栈顶元素操作对应获得 \(\textit{queue}_1\) 的前端元素,时间复杂度是 \(O(1)\)。
判断栈是否为空操作只需要判断 \(\textit{queue}_1\) 是否为空,时间复杂度是 \(O(1)\)。 -
空间复杂度:\(O(n)\),其中 n 是栈内的元素个数。需要使用两个队列存储栈内的元素。
单队列
方法二:一个队列
方法一使用了两个队列实现栈的操作,也可以使用一个队列实现栈的操作。
使用一个队列时,为了满足栈的特性,即最后入栈的元素最先出栈,同样需要满足队列前端的元素是最后入栈的元素。
入栈操作时,首先获得入栈前的元素个数 nn,然后将元素入队到队列,再将队列中的前 nn 个元素(即除了新入栈的元素之外的全部元素)依次出队并入队到队列,此时队列的前端的元素即为新入栈的元素,且队列的前端和后端分别对应栈顶和栈底。
由于每次入栈操作都确保队列的前端元素为栈顶元素,因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可,获得栈顶元素操作只需要获得队列的前端元素并返回即可(不移除元素)。
由于队列用于存储栈内的元素,判断栈是否为空时,只需要判断队列是否为空即可。

class MyStack {
Queue<Integer> queue;
/** Initialize your data structure here. */
public MyStack() {
queue = new LinkedList<Integer>();
}
/** Push element x onto stack. */
public void push(int x) {
int n = queue.size();
queue.offer(x);
for (int i = 0; i < n; i++) {
queue.offer(queue.poll());
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.poll();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
单调队列
可以用来维护(给定大小的)区间的最值,其时间复杂度为\(O(n)\),其中n为序列的元素个数。
适用场景:
- 最大最小值的队列
除了目标队列外,另外建立一个辅助队列,来存放目标队列的最大最小值。
注意:单调队列是双端队列!
以最大值辅助队列为例,我们需要保证队头元素为队内最大值,向下依次递减
-
辅助队列入队:当目标队列入队时,对比当前辅助队列队尾元素,为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
-
辅助队列出队:当目标队列出队时,对比当前辅助队列队头元素,如果相等,那辅助队列就出队
单调递增队列(队头到队尾单调递增)(将队头视为栈底,队尾视为栈顶,即 栈)
单调递增队列:保证队列头(栈底)元素一定是当前队列的最小值,用于维护区间的最小值。
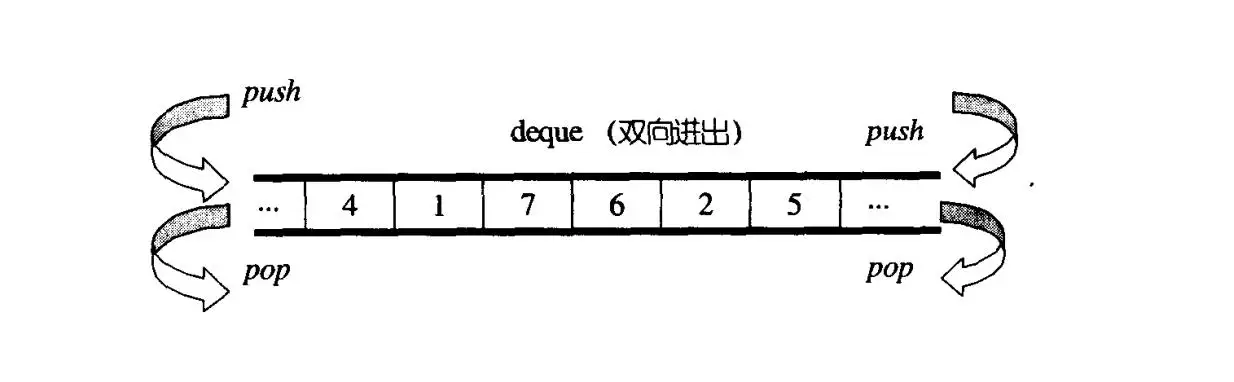
public void increasingDeque(int[] nums) {
Deque<Integer> deque = new Deque<>();
for (int num : nums) {
// 循环体内均为单调队列的入队操作
// 1. 入栈前将当前值小于等于栈顶元素,将栈顶元素弹出
while (!deque.isEmpty() && num <= deque.peekLast()) {
deque.pollLast();
}
deque.offerLast(num); // 2. 元素无论大小都是要入栈的
}
}
出队操作只需要比较队头元素与出队元素是否一致,如果一致即可出队。
单调递减队列(队头到队尾单调递减)(将队头视为栈底,队尾视为栈顶,即 栈)
单调递减队列:保证队列头元素一定是当前队列的最大值,用于维护区间的最大值。
public void decreasingStack(int[] nums) {
Deque<Integer> deque = new Deque<>();
for (int num : nums) {
// 循环体内均为单调队列的入队操作
// 1. 入栈前将当前值大于等于栈顶元素,将栈顶元素弹出
while (!deque.isEmpty() && num >= deque.peekLast()) {
deque.pollLast();
}
deque.offerLast(num); // 2. 元素无论大小都是要入栈的
}
}
给定数列:[3, 1, 5, 7, 4, 2, 1],现在要维护 区间长度为3 的最大值。
| 操作序号 | 操作 | 队列中元素 | 指定区间最大值 |
|---|---|---|---|
| ① | 3入队 | 3 | 区间大小不符合 |
| ② | 1入队 | 3, 1 | 区间大小不符合 |
| ③ | 3,1出队,5入队 | 5 | 区间[1,3]的最大值为5 |
| ④ | 5出队,7入队 | 7 | 区间[2,4]的最大值为7 |
| ⑤ | 4入队 | 7, 4 | 区间[3,5]的最大值为7 |
| ⑥ | 2入队 | 7, 4, 2 | 区间[4,6]的最大值为7 |
| ⑦ | 1入队,7出队 | 4, 2, 1 | 区间[5,7]的最大值为4 |
可以发现队列中的元素都是单调递减的(不然也就不叫单调递减队列啦),同时既有入队列的操作、也有出队列的操作。
滑动窗口 + 单调队列
一般单调队列都会配合固定滑动窗口一起使用
- 由滑动窗口来固定窗口大小
- 由单调队列来记录窗口内元素的最大最小值
// 初始化固定窗口
for (int i = left; i < right; i++) {
// 入队
while (maxQueue.peekLast() != null && nums[i] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[i]);
}
// 获取初始窗口的最大值
result[left] = maxQueue.peekFirst();
while (right < nums.length) {
// 右入队,左出队
// 每次出队都获取当前窗口的最大值
// 右入队
while (maxQueue.peekLast() != null && nums[right] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[right]);
// 左出队
if (nums[left] == maxQueue.peekFirst()) {
maxQueue.poll();
}
right++;
left++;
// 每移动一次窗口,就记录一次最大最小值
result[left] = maxQueue.peekFirst();
}
剑指 Offer 59 - II. 队列的最大值
请定义一个队列并实现函数 max_value 得到队列里的最大值,要求函数max_value、push_back 和 pop_front 的均摊时间复杂度都是O(1)。
若队列为空,pop_front 和 max_value 需要返回 -1
示例 1:
输入:
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出: [null,null,null,2,1,2]
示例 2:
输入:
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出: [null,-1,-1]
答案
如何思考
我们知道对于一个普通队列,push_back 和 pop_front 的时间复杂度都是 \(\mathcal{O}(1)\),因此我们直接使用队列的相关操作就可以实现这两个函数。
对于 max_value 函数,我们通常会这样思考,即每次入队操作时都更新最大值:

但是当出队时,这个方法会造成信息丢失,即 当最大值出队后,我们无法知道队列里的下一个最大值。
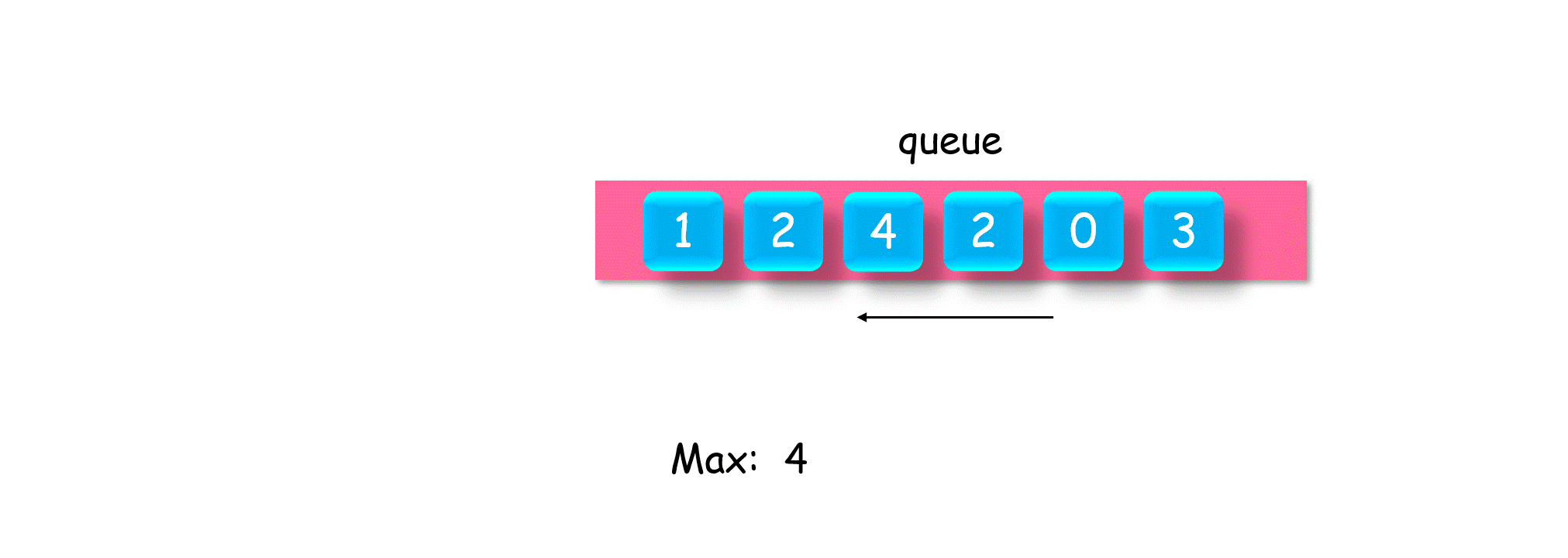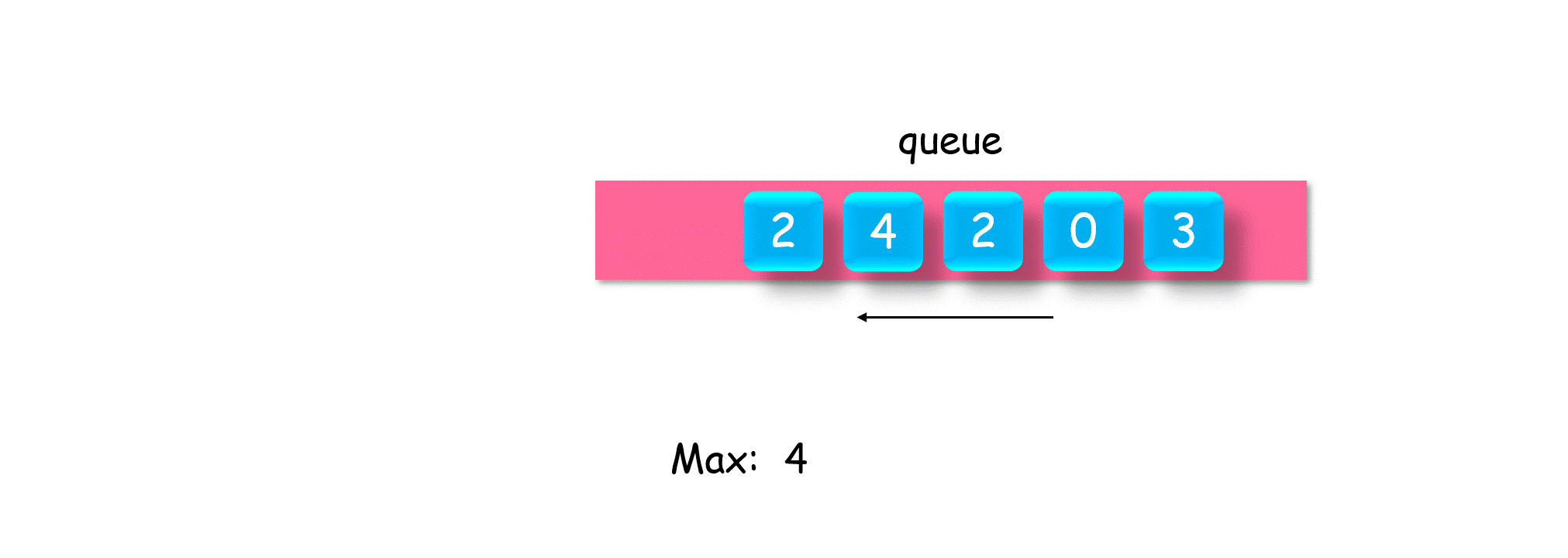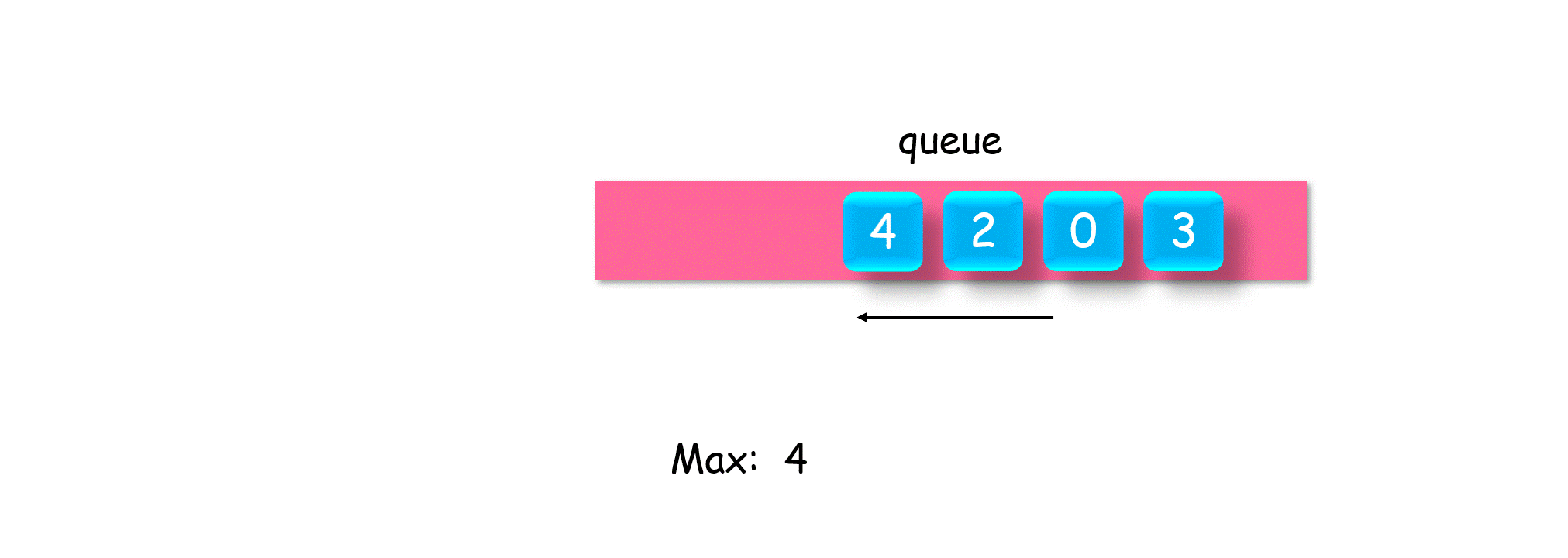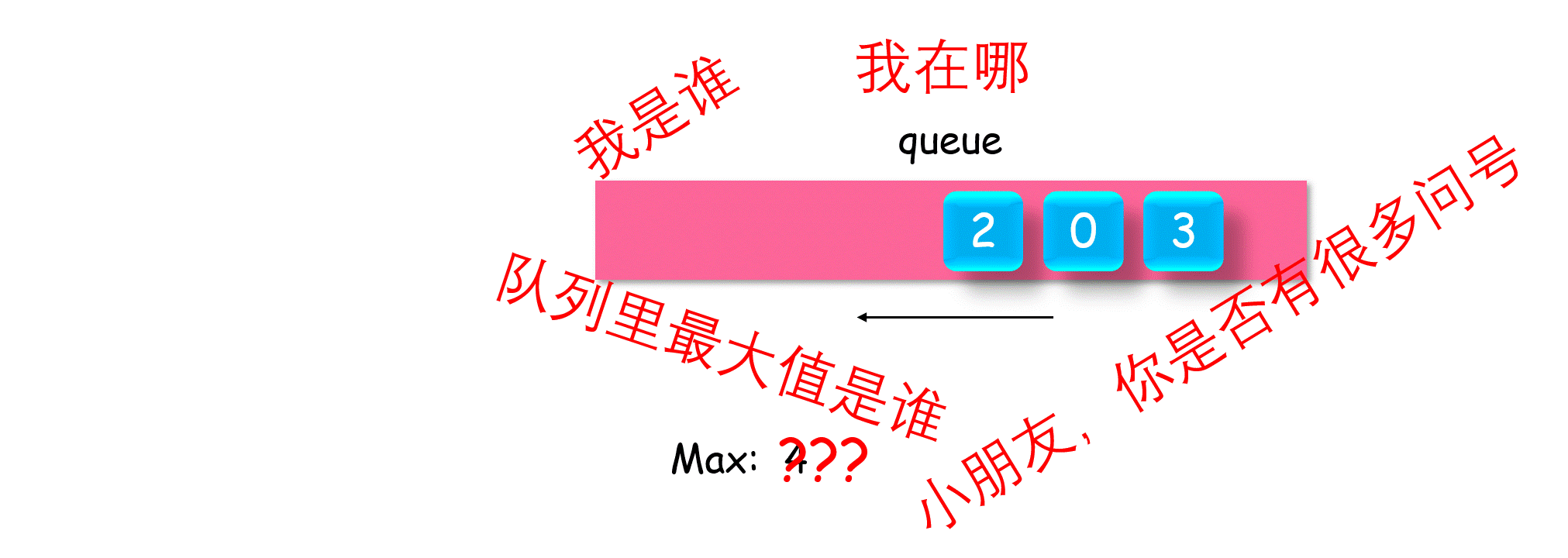
解题思路
为了解决上述问题,我们只需记住当前最大值出队后,队列里的下一个最大值即可。
具体方法是使用一个双端队列 deque,在每次入队时,如果 deque 队尾元素小于即将入队的元素 value,则将小于 value 的元素全部出队后,再将 value 入队;否则直接入队。

这时,辅助队列 deque 队首元素就是队列的最大值。
答案
维护一个非严格单调递减的双端队列,队头元素为当前最大值,向后依次递减
思路
本算法基于问题的一个重要性质:当一个元素进入队列的时候,它前面所有比它小的元素就不会再对答案产生影响。
举个例子,如果我们向队列中插入数字序列 1 1 1 1 2,那么在第一个数字 2 被插入后,数字 2 前面的所有数字 1 将不会对结果产生影响。因为按照队列的取出顺序,数字 2 只能在所有的数字 1 被取出之后才能被取出,因此如果数字 1 如果在队列中,那么数字 2 必然也在队列中,使得数字 1 对结果没有影响。
按照上面的思路,我们可以设计这样的方法:从队列尾部插入元素时,我们可以提前取出队列中所有比这个元素小的元素,使得队列中只保留对结果有影响的数字。这样的方法等价于要求维持队列单调递减,即要保证每个元素的前面都没有比它小的元素。
那么如何高效实现一个始终递减的队列呢?我们只需要在插入每一个元素 value 时,从队列尾部依次取出比当前元素 value 小的元素,直到遇到一个比当前元素大的元素 value 即可。
- 上面的过程保证了只要在元素 value 被插入之前队列递减,那么在 value 被插入之后队列依然递减。
- 而队列的初始状态(空队列)符合单调递减的定义。
- 由数学归纳法可知队列将会始终保持单调递减。
上面的过程需要从队列尾部取出元素,因此需要使用双端队列来实现。另外我们也需要一个辅助队列来记录所有被插入的值,以确定 pop_front 函数的返回值。
保证了队列单调递减后,求最大值时只需要直接取双端队列中的第一项即可。
class MaxQueue {
Queue<Integer> q;
Deque<Integer> d;
public MaxQueue() {
q = new LinkedList<Integer>();
d = new LinkedList<Integer>();
}
public int max_value() {
if (d.isEmpty()) {
return -1;
}
return d.peekFirst();
}
public void push_back(int value) {
while (!d.isEmpty() && d.peekLast() < value) {
d.pollLast();
}
d.offerLast(value);
q.offer(value);
}
public int pop_front() {
if (q.isEmpty()) {
return -1;
}
int ans = q.poll();
if (ans == d.peekFirst()) {
d.pollFirst();
}
return ans;
}
}
239. 滑动窗口最大值
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
示例:
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释:
滑动窗口的位置 最大值
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
提示:
1 <= nums.length <= 10^5
-10^4 <= nums[i] <= 10^4
1 <= k <= nums.length
我的
使用单调队列,队列元素从队头到队尾依次递减,队头元素为当前队列中的最大值
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
// 辅助队列
LinkedList<Integer> maxQueue = new LinkedList<>();
int left = 0, right = k;
int[] result = new int[nums.length - k + 1];
// 初始化窗口
for (int i = left; i < right; i++) {
// 入队
while (maxQueue.peekLast() != null && nums[i] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[i]);
}
// 获取初始窗口的最大值
result[left] = maxQueue.peekFirst();
while (right < nums.length) {
// 右入队,左出队
// 每次出队都获取当前窗口的最大值
while (maxQueue.peekLast() != null && nums[right] > maxQueue.peekLast()) {
maxQueue.removeLast();
}
maxQueue.offer(nums[right]);
if (nums[left] == maxQueue.peekFirst()) {
maxQueue.poll();
}
right++;
left++;
// 每移动一次窗口,就记录一次最大最小值
result[left] = maxQueue.peekFirst();
}
return result;
}
}
解答:
前言
对于每个滑动窗口,我们可以使用 \(O(k)\) 的时间遍历其中的每一个元素,找出其中的最大值。对于长度为 n 的数组 \(\textit{nums}\) 而言,窗口的数量为 \(n-k+1\),因此该算法的时间复杂度为 \(O((n-k+1)k)=O(nk)\),会超出时间限制,因此我们需要进行一些优化。
我们可以想到,对于两个相邻(只差了一个位置)的滑动窗口,它们共用着 \(k−1\) 个元素,而只有 1 个元素是变化的。我们可以根据这个特点进行优化。
方法一:优先队列
思路与算法
对于「最大值」,我们可以想到一种非常合适的数据结构,那就是优先队列(堆),其中的大根堆可以帮助我们实时维护一系列元素中的最大值。
对于本题而言,初始时,我们将数组 \(\textit{nums}\) 的前 k 个元素放入优先队列中。每当我们向右移动窗口时,我们就可以把一个新的元素放入优先队列中,此时堆顶的元素就是堆中所有元素的最大值。然而这个最大值可能并不在滑动窗口中,在这种情况下,这个值在数组 \(\textit{nums}\) 中的位置出现在滑动窗口左边界的左侧。因此,当我们后续继续向右移动窗口时,这个值就永远不可能出现在滑动窗口中了,我们可以将其永久地从优先队列中移除。
我们不断地移除堆顶的元素,直到其确实出现在滑动窗口中。此时,堆顶元素就是滑动窗口中的最大值。为了方便判断堆顶元素与滑动窗口的位置关系,我们可以在优先队列中存储二元组 \((\textit{num}, \textit{index})\),表示元素 \(\textit{num}\) 在数组中的下标为 \(\textit{index}\)。
代码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
public int compare(int[] pair1, int[] pair2) {
return pair1[0] != pair2[0] ? pair2[0] - pair1[0] : pair2[1] - pair1[1];
}
});
for (int i = 0; i < k; ++i) {
pq.offer(new int[]{nums[i], i});
}
int[] ans = new int[n - k + 1];
ans[0] = pq.peek()[0];
for (int i = k; i < n; ++i) {
pq.offer(new int[]{nums[i], i});
while (pq.peek()[1] <= i - k) {
pq.poll();
}
ans[i - k + 1] = pq.peek()[0];
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n \log n)\),其中 n 是数组 \(\textit{nums}\) 的长度。在最坏情况下,数组 \(\textit{nums}\) 中的元素单调递增,那么最终优先队列中包含了所有元素,没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 \(O(\log n)\),因此总时间复杂度为 \(O(n \log n)\)。
-
空间复杂度:\(O(n)\),即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 \(O(n)\) 空间,只计算额外的空间使用。
方法二:单调队列
思路与算法
我们可以顺着方法一的思路继续进行优化。
由于我们需要求出的是滑动窗口的最大值,如果当前的滑动窗口中有两个下标 i 和 j,其中 i 在 j 的左侧(i < j),并且 i 对应的元素不大于 j 对应的元素(\(\textit{nums}[i] \leq \textit{nums}[j]\)),那么会发生什么呢?
当滑动窗口向右移动时,只要 i 还在窗口中,那么 j 一定也还在窗口中,这是 i 在 j 的左侧所保证的。因此,由于 \(\textit{nums}[j]\) 的存在,\(\textit{nums}[i]\) 一定不会是滑动窗口中的最大值了,我们可以将 \(\textit{nums}[i]\) 永久地移除。
因此我们可以使用一个队列存储所有还没有被移除的下标。在队列中,这些下标按照从小到大的顺序被存储,并且它们在数组 \(\textit{nums}\) 中对应的值是严格单调递减的。因为如果队列中有两个相邻的下标,它们对应的值相等或者递增,那么令前者为 i,后者为 j,就对应了上面所说的情况,即 \(\textit{nums}[i]\) 会被移除,这就产生了矛盾。
当滑动窗口向右移动时,我们需要把一个新的元素放入队列中。为了保持队列的性质,我们会不断地将新的元素与队尾的元素相比较,如果前者大于等于后者,那么队尾的元素就可以被永久地移除,我们将其弹出队列。我们需要不断地进行此项操作,直到队列为空或者新的元素小于队尾的元素。
由于队列中下标对应的元素是严格单调递减的,因此此时队首下标对应的元素就是滑动窗口中的最大值。但与方法一中相同的是,此时的最大值可能在滑动窗口左边界的左侧,并且随着窗口向右移动,它永远不可能出现在滑动窗口中了。因此我们还需要不断从队首弹出元素,直到队首元素在窗口中为止。
为了可以同时弹出队首和队尾的元素,我们需要使用双端队列。满足这种单调性的双端队列一般称作「单调队列」。
代码
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
int n = nums.length;
Deque<Integer> deque = new LinkedList<Integer>();
for (int i = 0; i < k; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
}
int[] ans = new int[n - k + 1];
ans[0] = nums[deque.peekFirst()];
for (int i = k; i < n; ++i) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
while (deque.peekFirst() <= i - k) {
deque.pollFirst();
}
ans[i - k + 1] = nums[deque.peekFirst()];
}
return ans;
}
}
复杂度分析
-
时间复杂度:\(O(n)\),其中 n 是数组 \(\textit{nums}\) 的长度。每一个下标恰好被放入队列一次,并且最多被弹出队列一次,因此时间复杂度为 \(O(n)\)。
-
空间复杂度:\(O(k)\)。与方法一不同的是,在方法二中我们使用的数据结构是双向的,因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1 个元素,因此队列使用的空间为 \(O(k)\)。
笔者将不定期更新【考研或就业】的专业相关知识以及自身理解,希望大家能【关注】我。
如果觉得对您有用,请点击左下角的【点赞】按钮,给我一些鼓励,谢谢!
如果有更好的理解或建议,请在【评论】中写出,我会及时修改,谢谢啦!
本文来自博客园,作者:Nemo&
转载请注明原文链接:https://www.cnblogs.com/blknemo/p/11306065.html



 浙公网安备 33010602011771号
浙公网安备 33010602011771号