bzoj 1098 [POI2007] 办公楼 biu

# 解题思路

画画图可以发现，只要是两个点之间没有相互连边，那么就必须将这两个人安排到同一个办公楼内，如图所示：

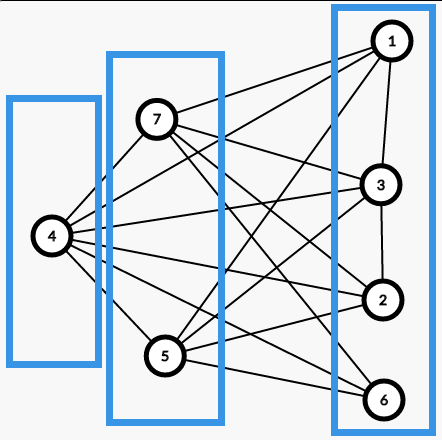
那，我们可以建立补图，就是先建一张完全图，然后把题目中给出的边都删掉，这就是一张补图，显然补图中相互连边的点就放在同一栋办公楼内。

我们可以用并查集来完成，但是数据范围显然不允许用这样的方法，建图的复杂度是 $N^2$ 的。所以考虑另一种方法：

将原图建立好，在原图中，从一个点开始，把这个点所能够直接到达的点标记出来，这些点是不可以放在一起的。然后将这些点删除。

之后对每一个点都进行这样的操作，那么之后要删除的点都要满足既没有被删除也没有被标记。这样做下来的复杂度还是 $N^2$ 的。再来想想如何优化，我们如果在删点的时候，不去枚举那些已经被删除的点。那所有的删点的操作总时间复杂度是 $M$ 的，因为每个边都要只遍历一次。如何优化？链表啊。。。

 

# 附上代码

#include <algorithm>
#include <iostream>
#include <cstring>
#include <cstdio>
#include <queue>
using namespace std;
template <typename T> inline void read(T &x) {
    x = 0; T f = 1; char c = getchar();
    while (c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
    while (c <= '9' && c >= '0') {x = x*10 + c-'0'; c = getchar();}
    x *= f;
}
const int maxn = 4e6+3;
int n, m, head[maxn], cnt, ans, pre[maxn], sur[maxn], num[maxn];
bool vis[maxn], del[maxn];
struct edge {int nxt, to;}ed[maxn];
inline void addedge(int x, int y) {
    ed[++cnt].nxt = head[x], head[x] = cnt, ed[cnt].to = y;
}
inline void DEL(int x) {
    sur[pre[x]] = sur[x];
    pre[sur[x]] = pre[x];
    del[x] = 1;
}
inline void BFS(int u) {
    queue<int> Q;
    Q.push(u), vis[u] = 1;
    while (!Q.empty()) {
        int now = Q.front();
        Q.pop();
        num[ans] ++;
        for(int i=head[now]; i; i=ed[i].nxt)
            vis[ed[i].to] = 1;
        for(int i=sur[0]; i<=n; i=sur[i])
            if(!vis[i] && !del[i]) Q.push(i), DEL(i);
        for(int i=head[now]; i; i=ed[i].nxt)
            vis[ed[i].to] = 0;
    }
}
int main() {
    read(n), read(m);
    int u, v;
    for(int i=1; i<=m; i++) {
        read(u), read(v);
        addedge(u, v), addedge(v, u);
    }
    for(int i=0; i<=n; i++)
        pre[i] = i-1, sur[i] = i+1;
    for(int i=1; i<=n; i++)
        if(!del[i]) del[i] = 1, ans ++, BFS(i), DEL(i);
    sort(num+1, num+1+ans);
    printf("%d\n", ans);
    for(int i=1; i<=ans; i++) printf("%d ", num[i]);
    return 0;
}