可持久化Trie
trie 有两种写法,一种是迭代,一种是递推,我比较喜欢递推,比较好想,代码也短。
带注释的代码
/*
开始理解可持久化, 这里因为是acwing打卡, 可以放图片了
有可能会用图片, 尽量打字
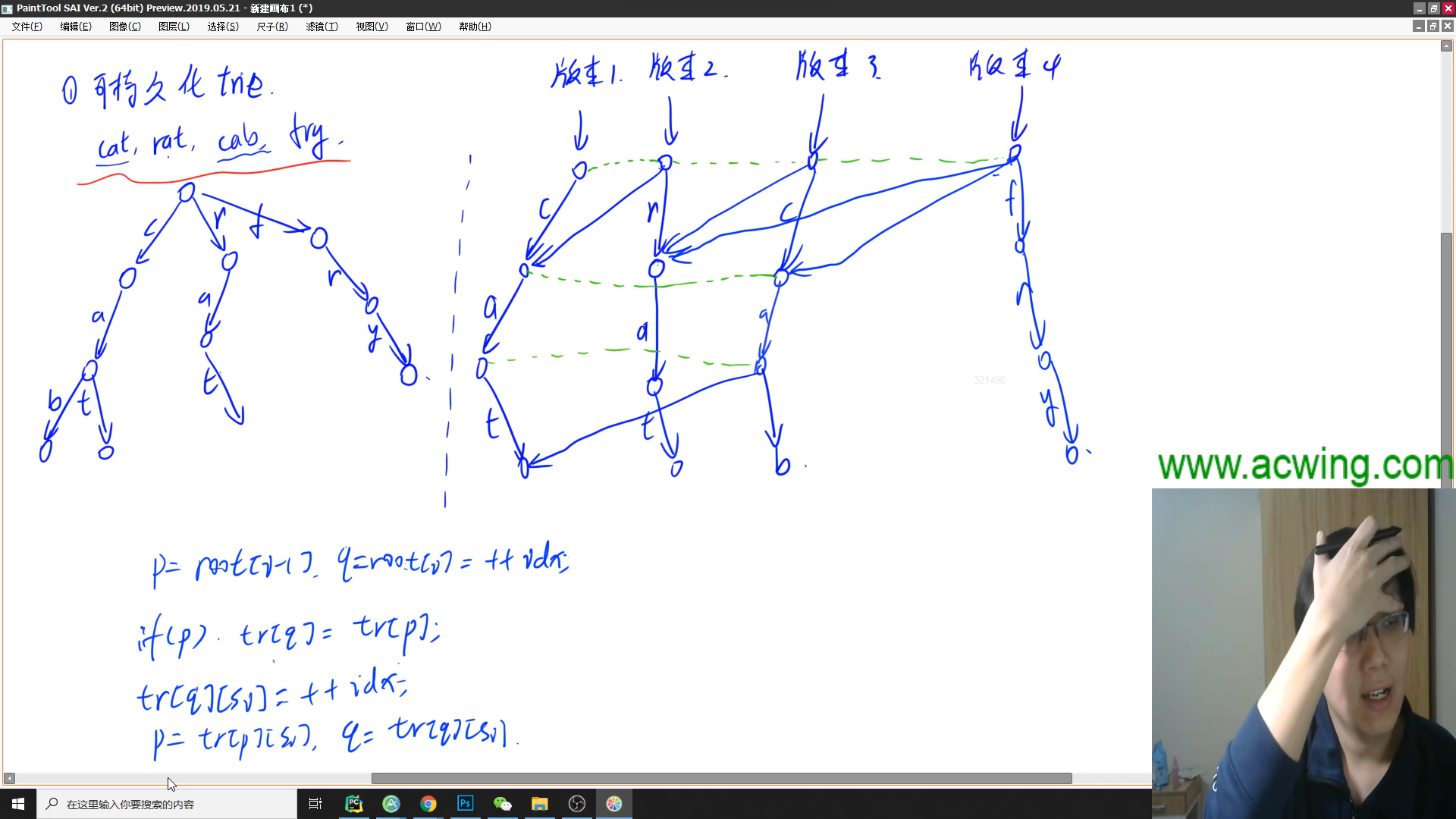
可持久化trie, 就是一个trie树但是可以通过不同的开头(root), 变成每个历史状态
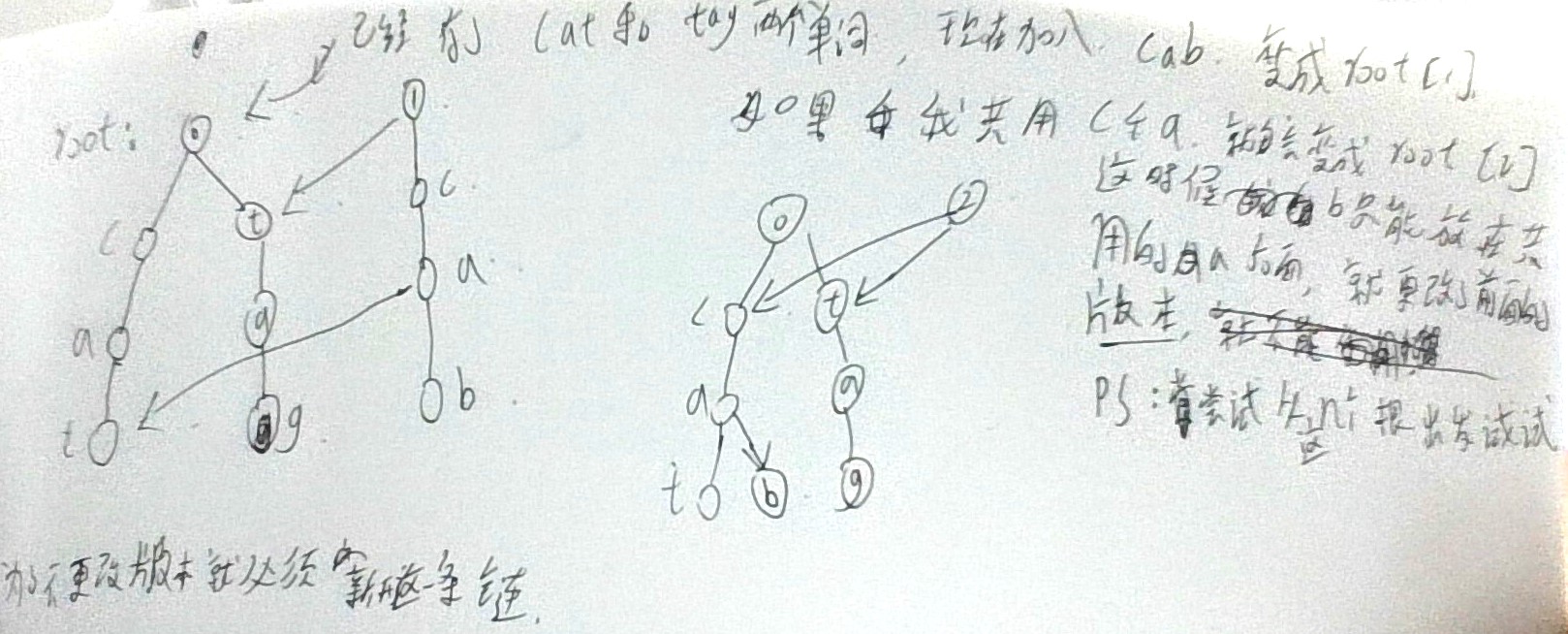
这里就用到上面的图片了, 每次更新trie树, 这条新加入的链一定要, 开成新的, 即使前面
有相同的的也不行(新加入的不能共用, 不然后面新的部分将更改前面的历史版本, 具体见上面图2)
p是上一版本, q是这一版本, 可持久化, 只针对于上一版本变化
总体思路就是, 每新加入一个东西, 看看这一层里面和它不同的, 向所有不同的连边(即tr[q][v] == tr[p][v]),
相当于复制了一边, 从这个根节点就可以, 通过这条边, 走到这些可以共用的
对于重复的, 比如cab和cat的c和a, 我们不向它们连边, 新开一个点, 继续进行上面的操作
说实话, 上来整01trie其实并不好, 但可持久化trie的题比较少, 后面我再打一个模版, 对于存单词的
这就是可持久化trie的思路
而对于这题, 有y的讲解, 很易懂, 我这里就粗略讲一下
我们先预处理出来异或前缀和, 然后你能发现一个神奇的性质, 我从l ^ (l + 1) ^ ... ^ r, 就等于sum[r] ^ sum[l - 1]
因为 5 ^ 3 ^ 5 == 3对吧, 相当于[1, r] ^ [1, l - 1] = [l, r]; // 这里的[i, j], 是 i ^ (i + 1) ^ ... ^ j得到的数
而我们是找一个再[l, r](这里指范围)里面的位置p, 然后求[p, n] ^ x, x是题目给出的某一个数
这玩意就等价于, sum[n] ^ sum[p - 1] ^ x, 然后这里面固定的值是, sum[n] ^ x 我们把这个数设为C
那么答案就是C ^ sum[p - 1]的最大值, p在[l, r]里面, 那么p - 1就在[l - 1, r - 1]里面;
也就是说在[l - 1, r - 1]里面选一个异或前缀和, 使得sum[i] ^ C最大
如果做过01trie的话就会发现, 这个玩意max(sum[i] ^ C)可以直接用01trie求出来(注意题目是让求最大值)
这就把这个问题转化为了, 01trie,
这时候就看看这个范围怎么整[l - 1, r - 1](下面简写为[l, r]),
r好弄, 我们可以发现, 可以用可持久化trie, 在第r个版本里面搜, 就可以限制住右边界(因为没有r之后的数)
现在就看左边界, 也好搞, 假设C这个数目前我拆分出来了1, 那么我最好选trie中的0
这样可以保留这个1, 那么就看看0这棵树里面有没有下标大于l的节点, 而有没有下标大于等于l的节点,
就等价于这颗子树里的最大下标是否大于等于l, 就每个数记录一个max_id, 如果这个大于等于l, 就可以选这个0,
就可以进到0树里面, 并保留这个1, 否则就走1树
这里求最大值可以像我一样保留1那样组合出这个数, 也可以通过找到那个点max_id[p]用sum[max_id[p]]去异或C
至此此题结束
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 600101, M = 25 * N;
int tr[M][2], n, m;
int max_id[M], root[N], idx;
LL sum[N];
void insert(int i, int k, int p, int q) // 这里可以写成迭代的形式, 但是为了求max_id方便, 所以用递归的形式
{
if (k < 0) // 说明到最后一个点
{
max_id[q] = i; // 那么最大下标就是它自己
return ;
}
int v = sum[i] >> k & 1;
if (p) tr[q][v ^ 1] = tr[p][v ^ 1]; // 连向另一边, 注意是连非当前点(v)的点的边, 并且这个点上一个版本必须有(没有的点我怎么共用, 凭空产生?)
tr[q][v] = ++ idx; // 新加点
insert(i, k - 1, tr[p][v], tr[q][v]); // 进入下一个点
max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]); // 在儿子里面求最大下标
}
int query(int root, int C, int L)
{
int p = root, res = 0; // res是组合出的这个数
for (int i = 23; i >= 0; i -- )
{
int v = C >> i & 1;
if (max_id[tr[p][!v]] >= L) p = tr[p][!v], res += 1 << i;
else p = tr[p][v];
}
return res; // 也可以写成 return C ^ sum[max_id[p]]; 因为最后p一定是异或最大的一条线里面的最后的一个点, 那么max_id[p]一定是异或C最大的
}
int main()
{
cin >> n >> m;
sum[0] = 0; // 开始的0, 因为可能会用到sum[0];
max_id[0] = -1; // 必须小于0, 因为为了防止l - 1 == 0时这个0号历史方案(实际上什么都没有)被选上了, max_id[tr[p][!v]] >= L, 如果小于0的话就可以防止这种情况
root[0] = ++ idx; // 这就是开始的0点
insert(0, 23, 0, root[0]);
for (int i = 1; i <= n; i ++ )
{
int w;
cin >> w;
sum[i] = sum[i - 1] ^ w;
root[i] = ++ idx;
insert(i, 23, root[i - 1], root[i]);
}
while (m -- )
{
char op[2];
int l, r, x;
scanf("%s", op);
if (*op == 'A')
{
scanf("%d", &x);
root[ ++ n] = ++ idx; // 注意这里 ++ n了长度已经变化了
sum[n] = sum[n - 1] ^ x;
insert(n, 23, root[n - 1], root[n]);
}
else
{
scanf("%d%d%d", &l, &r, &x);
printf("%d\n", query(root[r - 1], sum[n] ^ x, l - 1)); // 注意是l - 1, 和 r - 1
}
}
return 0;
}
updata 2024,6,26 自己想出的做法
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 300010 * 2, M = N * 24;
int tr[M][2], idx;
int n, m;
int sum[N], max_id[M];
int root[N];
void insert(int x, int p, int q, int L)
{
for (int i = 24; i >= 0; i -- )
{
int s = x >> i & 1;
if (p) tr[q][!s] = tr[p][!s];
q = tr[q][s] = ++ idx;
max_id[q] = max(max_id[p], L);
p = tr[p][s];
}
}
int query(int x, int p, int L)
{
int res = 0;
for (int i = 24; i >= 0; i -- )
{
int s = x >> i & 1;
if (tr[p][!s] && max_id[tr[p][!s]] >= L)
{
res += 1 << i;
p = tr[p][!s];
}
else p = tr[p][s];
}
return res;
}
int main()
{
cin >> n >> m;
root[0] = ++ idx;
insert(0, root[0], root[0], 0);
for (int i = 1; i <= n; i ++ )
{
cin >> sum[i];
sum[i] ^= sum[i - 1];
root[i] = ++ idx;
insert(sum[i], root[i - 1], root[i], i);
}
while (m -- )
{
char op[2];
int l, r, x;
scanf("%s", op);
if (op[0] == 'A')
{
scanf("%d", &x);
sum[n + 1] = sum[n] ^ x;
root[n + 1] = ++ idx;
insert(sum[n + 1], root[n], root[n + 1], n + 1);
n ++ ;
}
else
{
scanf("%d%d%d", &l, &r, &x);
x ^= sum[n];
l -- , r -- ;
printf("%d\n", query(x, root[r], l));
}
}
return 0;
}
通用模版
/*
通用的可持久化trie
具体干什么
给出n个字符串, 给出m个询问, 每个询问给出一个字符串s, 和一个限制r
问在前r个字符串里面是否有字符串s
如果有输出yes, 否则输出no
测试样例
3 4
a ab abc
ab 2
ab 1
abc 3
abc 2
yes
no
yes
no
*/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <ctime>
using namespace std;
const int N = 10010;
int tr[N][27], idx;
int n, m, cnt[N];
int root[N];
void insert(string s, int p, int q) // 这是迭代版本的写法, 下面的扩展模版里面有递归写法
{
for (int i = 0; s[i]; i ++ )
{
int v = s[i] - 'a';
for (int j = 0; j < 26; j ++ ) // 复制可用边, 这里的复杂度可以以优化
if (p && j != v) tr[q][j] = tr[p][j];
// memcpy(tr[q], tr[p], sizeof tr[p]); // 相对高效的写法, 当然也快不了太多,
q = tr[q][v] = ++ idx; // 走向下一个/建立新点
p = tr[p][v]; // 走向下一个
}
cnt[q] ++ ;
}
bool query(string s, int p)
{
for (int i = 0; s[i]; i ++ )
{
int v = s[i] - 'a';
if (!tr[p][v]) return false;
p = tr[p][v];
}
return cnt[p];
}
int main()
{
cin >> n >> m;
root[0] = ++ idx; // 也要初始化
insert("", root[0], root[0]);
for (int i = 1; i <= n; i ++ )
{
string s;
cin >> s;
// cout << s << endl;
root[i] = ++ idx;
insert(s, root[i - 1], root[i]);
}
while (m -- )
{
string s;
int r;
cin >> s >> r;
if (query(s, root[r])) puts("yes");
else puts("no");
}
cout << clock() << endl;
return 0;
}
扩展的通用模版
/*
通用的可持久化trie
具体干什么
给出n个字符串, 给出m个询问, 每个询问给出一个字符串s, 和限制[l, r]
问在[l, r]内的字符串里面是否有字符串s
如果有输出yes, 否则输出no
trie的每层的数量越多, 这玩意的消耗越大, 每次都得乘上以大常数, 所以一般都是01可持久化trie
这样就常数小
测试样例
3 4
a cbc ab
ab 2 3
cb 1 3
aaaa 1 3
ab 1 2
输出样例
yes
no
no
no
*/
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010;
int tr[N][27], idx;
int n, m, cnt[N];
int root[N], max_id[N];
// void insert(string s, int p, int q)
// {
// for (int i = 0; s[i]; i ++ )
// {
// int v = s[i] - 'a';
// for (int j = 0; j < 26; j ++ ) // 复制可用边, 这里的复杂度可以以优化
// if (p && j != v) tr[q][j] = tr[p][j];
// q = tr[q][v] = ++ idx; // 走向下一个/建立新点
// p = tr[p][v]; // 走向下一个
// }
// cnt[q] ++ ;
// }
void insert(int i, string s, int k, int p, int q) // 递归版本, 加上求 max_id; 当前的下标, 加入的串, 当前第几个字母, 上一个版本的这层, 这个版本的这层
{
if (!s[k])
{
max_id[q] = i;
cnt[q] ++ ;
return ;
}
int v = s[k] - 'a';
for (int j = 0; j < 26; j ++ )
if (p && j != v) tr[q][j] = tr[p][j];
tr[q][v] = ++ idx;
insert(i, s, k + 1, tr[p][v], tr[q][v]);
int maxv = -1;
for (int j = 0; j < 26; j ++ )
maxv = max(maxv, max_id[tr[q][j]]);
max_id[q] = maxv;
}
bool query(int l, string s, int p) // 递归的加上求max_id, 求区间的
{
for (int i = 0; s[i]; i ++ )
{
int v = s[i] - 'a';
if (!tr[p][v] || max_id[tr[p][v]] < l) return false;
p = tr[p][v];
}
return cnt[p];
}
// bool query(string s, int p) // 普通,
// {
// for (int i = 0; s[i]; i ++ )
// {
// int v = s[i] - 'a';
// if (!tr[p][v]) return false;
// p = tr[p][v];
// }
// return cnt[p];
// }
int main()
{
cin >> n >> m;
root[0] = ++ idx;
for (int i = 1; i <= n; i ++ )
{
string s;
cin >> s;
root[i] = ++ idx;
insert(i, s, 0, root[i - 1], root[i]);
}
while (m -- )
{
string s;
int l, r;
cin >> s >> l >> r;
if (query(l, s, root[r])) puts("yes");
else puts("no");
}
return 0;
}
图片
图一
图二
图三
图四