欧拉函数（新）

这是重新整理的欧拉函数，会把欧拉函数的一些性质说出来。

欧拉函数即 \(\varphi(i)\)，表示从 \([1, i]\) 之间和 \(i\) 互质的数的数量 （ \(a\) 和 \(b\) 互质即 \(\gcd(a, b) = 1\)）。
注意当 \(i=1\) 时，\(\varphi(1) = 1\)。

递推公式（积性）

欧拉函数有一个算是递推式的东西，即对于任意正整数 \(a\)：

\[φ(ab) = \frac {φ(a) \times φ(b) \times \gcd(a,b)}{φ(\gcd(a,b))} \]

易得，当 \(a,b\) 互质时，有：

\[\varphi(ab) = \varphi(a) \times\varphi(b) \]

证明

利用计算公式证明，你可以直接把计算公式带进去直接化，设 \(d = \gcd(a,b)\) 那么可得

\[\begin{aligned} φ(ab) &= \frac {φ(a) \times φ(b) \times \gcd(a,b)}{φ(\gcd(a,b))} \\ &= \frac{a\prod_{i=1}^{k_a} \left(1-\frac{1}{p_i}\right) \times b\prod_{i=1}^{k_b} \left(1-\frac{1}{p_i}\right) \times d} {d\prod_{i=1}^{k_d} \left(1-\frac{1}{p_i}\right)} \\ &= \frac{a\prod_{i=1}^{k_a} \left(1-\frac{1}{p_i}\right) \times b\prod_{i=1}^{k_b} \left(1-\frac{1}{p_i}\right)} {\prod_{i=1}^{k_d} \left(1-\frac{1}{p_i}\right)} \end{aligned} \]

因为 d 是 \(a,b\) 的最大公约数，那么分母上的 \(\prod_{i=1}^{k_d} \left(1-\frac{d}{p_i}\right)\) 就可以把 \(a\prod_{i=1}^{k_a} \left(1-\frac{1}{p_i}\right) \times b\prod_{i=1}^{k_b} \left(1-\frac{1}{p_i}\right)\) 中 \(a,b\) 的 \(\left( 1 - \frac{1}{p_i} \right)\) 中相同的部分给消掉一个，剩下的就不重复，且乘起来就恰好就是 \(ab\prod_{i=1}^{k_{ab}} \left(1-\frac{1}{p_i}\right)\)，也就是 \(\varphi(ab)\)。因为 \(a,b\) 含有 \(ab\) 的所有质因子。
证毕。
这也就证明了欧拉函数是积性函数。

计算公式（通项式）

即：

\[\varphi(N) = N \times (1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times \ldots \times (1 - \frac{1}{p_k}), \quad N \in \text Z, p_i \text{ is prime} \]

利用积性证明

欧拉函数是积性函数，例如 \(a, b\) 都为正整数，有递推式为

\[φ(ab) = \frac {φ(a) \times φ(b) \times \gcd(a,b)}{φ(\gcd(a,b))} \]

当 \(a,b\) 互质时，则有

\[φ(ab) = φ(a) \times φ(b) \]

下面开始证明
设一个正整数 \(N\)，把它分解成质数，可得

\[N = p_1^{b_1} \times p_{2}^{b_2} \times p_{3}^{b_3} \times \ldots \times p_{k}^{b_k} ,\quad p_i \text{ is prime} \]

又因为 当 \(a,b\) 互质时

\[\displaylines { \varphi(ab) = \varphi(a) \times φ(b), \quad \gcd(a, b) = 1 \\ } \]

所以

\[\displaylines{ \varphi(N) = \varphi(p_1^{b_1}) \times \varphi(p_2^{b_2}) \times \varphi(p_3^{b_3}) \times \ldots \times \varphi(p_k^{b_k}) } \]

因为对于 \(\varphi(p_b)\) 来说，\([1, p^b]\) 一共有 \(p^b\) 个数。其中不与 \(p^b\) 互质的数是 \(1p, 2p, 3p, \ldots, p^{b-1} \times p\) ，总共 \(p^{b-1}\) 个，剩下的就是和 \(p_b\) 互质的数，共 \(p^b - p^{b-1}\) 个数。
即

\[φ(p^b) = p^b \times (1 - \frac{1}{p}) \]

因为

\[\displaylines{ \varphi(N) = \varphi(p_1^{b_1}) \times \varphi(p_2^{b_2}) \times \varphi(p_3^{b_3}) \times \ldots \times \varphi(p_k^{b_k}) \\ \varphi(p^b) = p^b - p^{b-1} } \]

可得

\[\varphi(N) = p_1^{b_1} (1 - \frac{1}{p_1}) \times p_2^{b_2}(1 - \frac{1}{p_2}) \times \ldots \times p_k^{b_k}(1 - \frac{1}{p_k}) \]

即

\[\varphi(N) = (p_1^{b_1} \times p_2^{b_2} \times \ldots \times p_k^{b_k}) \times (1 - \frac{1}{p_1})(1 - \frac{1}{p_2}) \ldots (1 - \frac{1}{pk}) \]

又因为

\[N = p_1^{b_1} \times p_2^{b_2} \times \ldots \times p_k^{b_k} \]

可得

\[\varphi(N) = N \times (1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times \ldots \times (1 - \frac{1}{p_k}) \]

利用容斥定理

设一个正整数 \(N\)

由算数的基本定理得

\[N = p_1^{b_1} \times p_{2}^{b_2} \times p_{3}^{b_3} \times \ldots \times p_{k}^{b_k} ,\quad p_i \text{ is prime} \]

对于 \(\varphi(N)\) 来说，求和 \(N\) 互质的数，也就是求和 \(N\) 不互质的数的数量。
那么对于分解出的一个质数 \(p_i\) 来说，在 \([1, N]\) 里面和它不互质的数就为 \(p_i\) 的倍数，共 \(\frac{N}{p_i}\) 个，但这个数量肯定要比和 \(N\) 不互质的数的数量多。我们可以画一个韦恩图来看。

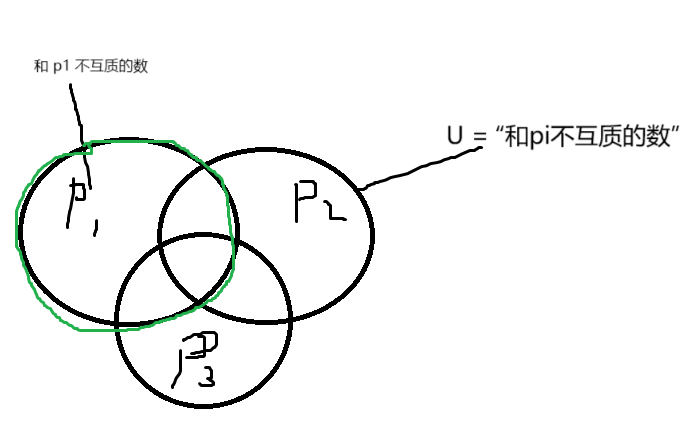
我们要求和 \(N\) 不互质的数 \(m\)，那么 \(m\) 只需要和任意一个 \(p_i\) 不互质即可，即上图的全集。
那么这就可以用容斥定理求出全集了。而这里的 \(p_i\) 和 \(p_j\) 的交集数量即为 \(\frac{N}{p_ip_j}\)。

很容易可以得到

\[\varphi(N) = N - (\sum_{i = 1}^{k}(\frac{N}{p_i}) - \sum_{i = 1}^{k} \sum_{j}^{i < j \le k}(\frac{N}{p_i p_j}) + \ldots ) \]

而这个式子可以化为

\[\varphi(N) = N \times (1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times \ldots \times (1 - \frac{1}{p_k}) \]

可以发现上面两个式子是等价的。可以这么理解，对于 \((1 - \frac{1}{p_i})\) 来说，我们选取一个这个式子里的 \(-\frac{1}{p_i}\) 其他的选 \(1\)，那么最后得出的就是 \(-\frac{1}{p_i}\)，如果选两个 \(p_i\)，其他的选 \(1\)，得出来的也就是 \(\frac{1}{p_ip_j}\) ，选三个 \(p_i\)，其他选 \(1\)，得出的就是 \(-\frac{1}{p_ip_jp_k}\)，而这恰好就是容斥定理的进行形式。也就是说这两个是等价的

总结

于是就可以通过分解 \(N\) 的质因数求出来 \(\varphi(N)\)，由此也可以看出，一个数的欧拉函数的大小和质数的次幂无关。

试除法分解质因数是 \(O(\sqrt n)\) 的, 所以求 \(\varphi(N)\) 也就是 \(O(\sqrt n)\) 的
具体见代码

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

int n, m;

int main()
{
    int T;
    cin >> T;
    while (T -- )
    {
        cin >> n;
        int res = n;
        for (int i = 2; i <= n / i; i ++ )
        {
            if (n % i == 0) 
            {
                res = res / i * (i - 1); // 相当于res * (1 - 1 / i), 这样是为了防止出现小数, 下取整没了, 最主要的就是这里
                while (n % i == 0) n /= i;
            }
        }
        if (n != 1) res = res / n * (n - 1); // 这里不要忘记
        cout << res << endl;
    }
    return 0;
}

一个数欧拉函数的大小和质因数的次幂无关

更快点？要不要试试先把质数筛出来？这样也可减少一定的时间。

筛法求欧拉函数

\(O(n)\)
这里写的注释很好，就不多重打了。
是用线性筛顺便筛出欧拉函数，首先，线性筛可以筛出质数 p，质数的欧拉函数很好求，因为一个质数在 \([1, p]\) 中除了 p 本身以外，其他所有数都与它互质，所以 \(\varphi(p) = p - 1\)。
而对于筛掉的数，我们可以知道，筛掉的数是用这个数 u 的最小质因子 p 筛去的，唉？质因子是质数吧，按算法运行顺序来说， u 是由 \(p \times i\) 得到的，那么 i 是整数，且肯定比 u 小，按理说，它的欧拉函数我已经求出来了。而 \(\varphi(p) = p - 1\)，我们还知道一个等式。
即

\[\varphi(ab) = \frac {φ(a) \times φ(b) \times \gcd(a,b)}{φ(\gcd(a,b))} \]

那么就可以得出来了

\[\varphi(u) = \varphi(i \times p) = \frac {\varphi(p) \times \varphi(i) \times \gcd(p,i)}{\varphi(\gcd(i,p))} \]

其中因为 \(p\) 是质数，而 \(p <= i\) ，并且 p 是 i 的质因子，所以 \(\gcd(i,p) = p\)，所以 \(\varphi(\gcd(p,i)) = \varphi(p)\)
所以有下式

\[\varphi(u) = \varphi(i \times p) = {p \times \varphi(i)} \]

在注释里还有一种解释方法，这里就不说了。

/*
    线性筛可以求出很多附加的东西
    具体会在代码里写注释
*/

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 1000010;

int n;
int primes[N], cnt;
bool st[N];
int phi[N]; // phi[i] 是i的欧拉函数
LL sum;

int main()
{
    cin >> n;
    phi[1] = 1; // 1的欧拉函数是1, 需要手动写上
    for (int i = 2; i <= n; i ++ )
    {
        if (st[i] == 0)
        {
            primes[ ++ cnt] = i;
            sum += phi[i] = i - 1; // 首先如果i是质数, 质数和所有数都互质(除了它自己), 那么对于质数i的φ, 就是i - 1
        }
        for (int j = 1; primes[j] <= n / i; j ++ )
        {
            st[i * primes[j]] = true;
            if (i % primes[j] == 0) // 如果i % pj == 0 那么pj就是i的最小质因数(这点在线性筛里提到过)
            { // 说明i的质因数包括pj, 那么φ(i)里面包括 (1 - 1/pj), 一个数欧拉函数的大小和其质因数的次幂无关, 根据φ(N) = N * (1 - 1/p1) * (1 - 1/p2) * ... * (1 - 1/pk);
                sum += phi[i * primes[j]] = phi[i] * primes[j]; // pj * i 比 i 只多了一个pj而且pj还在i的质因数里面, 那么 φ(i*pj)只比φ(i)多一个pj 也就是 φ(i*pj) = φ(i) * pj
                break;
            }
            sum += phi[i * primes[j]] = phi[i] * (primes[j] - 1); // 和上面同理, 但是pj不是i的质因数, 所以φ(i) 不包含 (1 - 1/pj), φ(pj*i)需要加上这个 
        }
    }
    cout << sum + 1 << endl;
    
    return 0;
}